Local-global principles for large rings of algebraic integers
Let 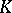 be a global field. In other words,
be a global field. In other words, 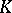 is either a number field, i.e. a finite extension of
is either a number field, i.e. a finite extension of 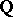 , or a function field of one variable over a finite field. Denote the algebraic (respectively, separable) closure of
, or a function field of one variable over a finite field. Denote the algebraic (respectively, separable) closure of 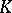 by
by 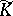 (respectively, by
(respectively, by 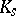 ; cf. also Extension of a field). A prime divisor of
; cf. also Extension of a field). A prime divisor of 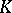 is an equivalence class
is an equivalence class 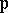 of absolute values (cf. also Norm on a field). For each
of absolute values (cf. also Norm on a field). For each 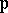 , let
, let 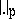 be a representative of
be a representative of 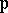 . Denote the completion of
. Denote the completion of 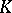 at
at 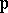 by
by 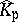 . Then
. Then 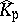 is either
is either 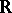 or
or 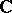 (
(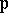 is metric), or
is metric), or  is a finite extension of
is a finite extension of 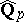 or a finite extension of
or a finite extension of 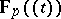 (
(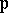 is ultra-metric).
is ultra-metric).
There is a natural 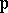 -topology on
-topology on 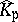 whose basic
whose basic 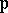 -open subsets have the form
-open subsets have the form 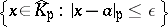 , for
, for 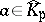 and
and 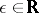 ,
, 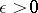 . The
. The 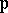 -topology has compatible extensions to all sets
-topology has compatible extensions to all sets 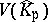 , where
, where 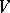 is an affine algebraic set over
is an affine algebraic set over  . In each case,
. In each case, 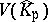 is locally compact.
is locally compact.
Embed  into the algebraic closure of
into the algebraic closure of 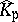 and let
and let 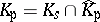 . Then
. Then 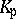 is a real (respectively, algebraic) closure of
is a real (respectively, algebraic) closure of 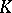 at
at 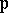 if
if 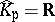 (respectively,
(respectively, 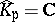 ), and is a Henselization of
), and is a Henselization of 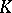 at
at 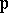 if
if 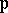 is ultra-metric (cf. also Henselization of a valued field). In the latter case, the valuation ring of
is ultra-metric (cf. also Henselization of a valued field). In the latter case, the valuation ring of 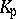 is denoted by
is denoted by 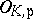 . In each case,
. In each case, 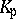 is uniquely determined up to a
is uniquely determined up to a 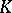 -isomorphism.
-isomorphism.
If 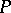 is a set of prime divisors of
is a set of prime divisors of 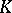 and
and  is an algebraic extension of
is an algebraic extension of  , then
, then 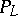 denotes the set of all extensions to
denotes the set of all extensions to 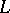 of all
of all 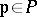 .
.
In the sequel, let 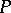 be a fixed set of prime divisors of
be a fixed set of prime divisors of 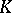 which does not contain all prime divisors. For each algebraic extension
which does not contain all prime divisors. For each algebraic extension 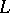 of
of 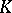 and each
and each 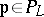 , let
, let 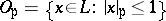 . Thus, if
. Thus, if 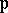 is metric, then
is metric, then 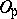 is the
is the 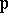 -unit ball and if
-unit ball and if 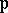 is ultra-metric, then
is ultra-metric, then 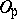 is the valuation ring of
is the valuation ring of 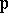 . Let
. Let 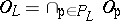 . If
. If 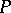 consists of ultra-metric primes only, then
consists of ultra-metric primes only, then 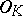 is a Dedekind domain (cf. also Dedekind ring). For example, if
is a Dedekind domain (cf. also Dedekind ring). For example, if  and
and  consists of all prime numbers, then
consists of all prime numbers, then 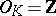 .
.
Fix also a finite subset 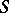 of
of 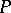 . Consider the field of totally
. Consider the field of totally 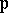 -adic numbers:
-adic numbers:
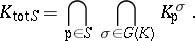 |
This is the largest Galois extension of 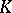 in which each
in which each 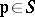 totally splits. Let
totally splits. Let 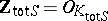 . If
. If 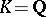 ,
, 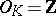 and
and 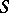 is empty, then
is empty, then  and
and 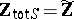 is the ring of all algebraic integers. The following two theorems, which can be found in [a10] and [a4], are therefore generalizations of Rumely's local-global principle and the density theorem (cf. also Local-global principles for the ring of algebraic integers).
is the ring of all algebraic integers. The following two theorems, which can be found in [a10] and [a4], are therefore generalizations of Rumely's local-global principle and the density theorem (cf. also Local-global principles for the ring of algebraic integers).
The local-global principle: In the above notation, let 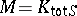 . Consider an absolutely irreducible affine variety
. Consider an absolutely irreducible affine variety 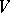 over
over 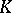 . Suppose that
. Suppose that 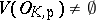 for each
for each 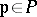 . Suppose further that
. Suppose further that 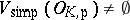 for each
for each 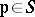 . Then
. Then 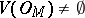 .
.
Here, 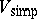 is the Zariski-open subset of
is the Zariski-open subset of 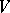 consisting of all non-singular points.
consisting of all non-singular points.
The density theorem: Let 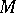 and
and 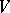 be as in the local-global principle. Let
be as in the local-global principle. Let 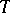 be a finite subset of
be a finite subset of 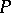 containing
containing 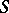 . Suppose that
. Suppose that 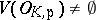 for each
for each 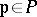 . For each
. For each 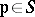 , let
, let 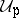 be a non-empty
be a non-empty 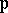 -open subset of
-open subset of 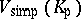 . For each
. For each 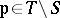 , let
, let 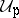 be a non-empty
be a non-empty 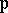 -open subset of
-open subset of 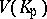 . Then
. Then 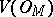 contains a point which lies in
contains a point which lies in 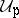 for each
for each  .
.
Although the density theorem looks stronger than the local-global principle, one can actually use the weak approximation theorem and deduce the density theorem from the local-global principle.
Both the local-global principle and the density theorem are actually true for fields 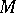 which are much smaller than
which are much smaller than 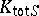 . To this end, call a field extension
. To this end, call a field extension 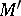 of
of 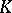 PAC over
PAC over 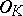 if for every dominating separable rational mapping
if for every dominating separable rational mapping 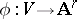 of absolutely irreducible varieties of dimension
of absolutely irreducible varieties of dimension  over
over 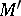 , there exists an
, there exists an 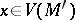 such that
such that 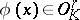 . If
. If 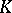 is a number field and
is a number field and 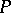 consists of ultra-metric primes only, [a8], Thm. 1.4; 1.5, imply both the density theorem and the local-global principle for
consists of ultra-metric primes only, [a8], Thm. 1.4; 1.5, imply both the density theorem and the local-global principle for 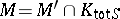 . In the function field case, [a8] must replace
. In the function field case, [a8] must replace 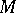 by its maximal purely inseparable extension, which is denoted by
by its maximal purely inseparable extension, which is denoted by 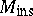 . Accordingly, the fields
. Accordingly, the fields 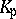 in the assumption of the density theorem and the local-global principle must be replaced by
in the assumption of the density theorem and the local-global principle must be replaced by 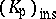 . However, using the methods of [a4] and [a5], it is plausible that even in this case one can restore the theorem for
. However, using the methods of [a4] and [a5], it is plausible that even in this case one can restore the theorem for 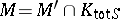 .
.
By Hilbert's Nullstellensatz (cf. also Hilbert theorem), 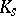 is PAC over
is PAC over 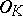 . Hence, [a8], Thms.1.4; 1.5, generalize the density theorem and the local-global principle above. Probability theory supplies an abundance of other algebraic extensions of
. Hence, [a8], Thms.1.4; 1.5, generalize the density theorem and the local-global principle above. Probability theory supplies an abundance of other algebraic extensions of 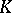 which are PAC over
which are PAC over 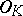 . The measure space in question is the Cartesian product
. The measure space in question is the Cartesian product 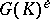 of
of  copies of the absolute Galois group of
copies of the absolute Galois group of 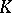 equipped with the Haar measure. For each
equipped with the Haar measure. For each 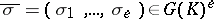 , let
, let 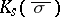 be the fixed field of
be the fixed field of  in
in 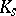 . By [a7], Prop. 3.1,
. By [a7], Prop. 3.1, 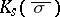 is PAC over
is PAC over 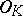 for almost all
for almost all 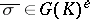 . Together with the preceding paragraph, this yields the following result (the Jarden–Razon theorem): For every positive integer
. Together with the preceding paragraph, this yields the following result (the Jarden–Razon theorem): For every positive integer  and for almost all
and for almost all 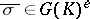 , the field
, the field 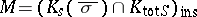 satisfies the conclusions of the local-global principle and the density theorem.
satisfies the conclusions of the local-global principle and the density theorem.
The local-global principle for rings implies a local-global principle for fields. An algebraic extension 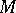 of
of 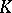 is said to be P
is said to be P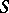 C (pseudo
C (pseudo  -adically closed) if each absolutely irreducible variety
-adically closed) if each absolutely irreducible variety  over
over 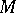 which has a simple
which has a simple 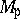 -rational point for each
-rational point for each 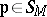 , has an
, has an 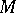 -rational point. In particular, by the local-global principle and the Jarden–Razon theorem, the fields
-rational point. In particular, by the local-global principle and the Jarden–Razon theorem, the fields 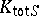 and
and 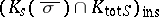 are P
are P C for almost all
C for almost all  . The main result of [a5] supplies P
. The main result of [a5] supplies P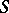 C extensions of
C extensions of 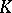 which are even smaller than the fields
which are even smaller than the fields 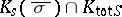 (the Geyer–Jarden theorem): For every positive integer
(the Geyer–Jarden theorem): For every positive integer  and for almost all
and for almost all 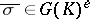 , the field
, the field 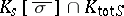 is P
is P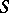 C.
C.
Here, 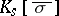 is the maximal Galois extension of
is the maximal Galois extension of 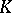 that is contained in
that is contained in 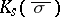 . It is not known (1998) whether
. It is not known (1998) whether 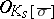 satisfies the local-global principle. (So, the Geyer–Jarden theorem is not a consequence of the Jarden–Razon theorem.) Since a separable algebraic extension of a P
satisfies the local-global principle. (So, the Geyer–Jarden theorem is not a consequence of the Jarden–Razon theorem.) Since a separable algebraic extension of a P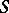 C field is P
C field is P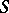 C [a9], Lemma 7.2, the Geyer–Jarden theorem implies that
C [a9], Lemma 7.2, the Geyer–Jarden theorem implies that 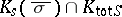 is P
is P C for almost all
C for almost all 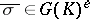 . Likewise, it reproves that
. Likewise, it reproves that 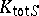 is P
is P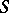 C.
C.
A field  which is P
which is P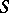 C is also ample (i.e. if
C is also ample (i.e. if 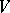 is an absolutely irreducible variety over
is an absolutely irreducible variety over 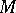 and
and 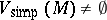 , then
, then 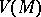 is Zariski-dense in
is Zariski-dense in 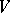 ). Ample fields, in particular P
). Ample fields, in particular P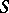 C fields, have the nice property that the inverse problem of Galois theory over
C fields, have the nice property that the inverse problem of Galois theory over  has a positive solution (cf. also Galois theory, inverse problem of). That is, for every finite group
has a positive solution (cf. also Galois theory, inverse problem of). That is, for every finite group 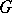 there exists a Galois extension
there exists a Galois extension 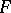 of
of 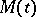 such that
such that 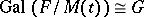 . Indeed, every finite split embedding problem over
. Indeed, every finite split embedding problem over 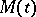 is solvable [a11], Main Thm. A, [a6], Thm. 2.
is solvable [a11], Main Thm. A, [a6], Thm. 2.
Another interesting consequence of the local-global principle describes the absolute Galois group of 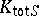 : It is due to F. Pop [a11], Thm. 3, and may be considered as a local-global principle for the absolute Galois group of
: It is due to F. Pop [a11], Thm. 3, and may be considered as a local-global principle for the absolute Galois group of 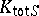 (Pop's theorem): The absolute Galois group of
(Pop's theorem): The absolute Galois group of 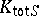 is the free pro-finite product
is the free pro-finite product
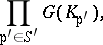 |
where 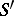 is the set of all extensions to
is the set of all extensions to 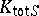 of all
of all 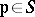 . This means that if
. This means that if  is a finite group, then each continuous mapping
is a finite group, then each continuous mapping 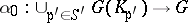 whose restriction to each
whose restriction to each 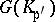 is a homomorphism, can be uniquely extended to a homomorphism
is a homomorphism, can be uniquely extended to a homomorphism 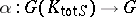 .
.
As a consequence of the local-global principle, Yu.L. Ershov [a2], Thm. 3, has proved that the elementary theory of 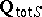 is decidable. If
is decidable. If 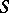 does not contain
does not contain 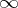 , this implies, by [a1], p. 86; Corol. 10, that the elementary theory of
, this implies, by [a1], p. 86; Corol. 10, that the elementary theory of 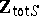 is decidable. In particular, Hilbert's tenth problem has an affirmative solution over
is decidable. In particular, Hilbert's tenth problem has an affirmative solution over 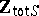 . If however,
. If however, 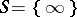 , then the elementary theory of
, then the elementary theory of  is decidable [a3] but the elementary theory of
is decidable [a3] but the elementary theory of 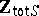 is undecidable [a12].
is undecidable [a12].
References
| [a1] | L. Darnière, "Étude modèle-théorique d'anneaus satisfaisant un principe de Hasse non singulier" PhD Thesis (1998) |
| [a2] | Yu.L. Ershov, "Nice local-global fields I" Algebra and Logic , 35 (1996) pp. 229–235 |
| [a3] | M.D. Fried, D. Haran, H. Völklein, "Real hilbertianity and the field of totally real numbers" Contemp. Math. , 74 (1994) pp. 1–34 |
| [a4] | B. Green, F. Pop, P. Roquette, "On Rumely's local-global principle" Jahresber. Deutsch. Math. Ver. , 97 (1995) pp. 43–74 |
| [a5] | W.-D. Geyer, M. Jarden, "PSC Galois extensions of Hilbertian fields" Manuscript Tel Aviv (1998) |
| [a6] | D. Haran, M. Jarden, "Regular split embedding problems over function fields of one variable over ample fields" J. Algebra , 208 (1998) pp. 147–164 |
| [a7] | M. Jarden, A. Razon, "Pseudo algebraically closed fields over rings" Israel J. Math. , 86 (1994) pp. 25–59 |
| [a8] | M. Jarden, A. Razon, "Rumely's local global principle for algebraic P C fields over rings" Trans. Amer. Math. Soc. , 350 (1998) pp. 55–85 C fields over rings" Trans. Amer. Math. Soc. , 350 (1998) pp. 55–85 |
| [a9] | M. Jarden, "Algebraic realization of 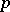 -adically projective groups" Compositio Math. , 79 (1991) pp. 21–62 -adically projective groups" Compositio Math. , 79 (1991) pp. 21–62 |
| [a10] | L. Moret-Bailly, "Groupes de Picard et problèmes de Skolem II" Ann. Sci. Ecole Norm. Sup. , 22 (1989) pp. 181–194 |
| [a11] | F. Pop, "Embedding problems over large fields" Ann. of Math. , 144 (1996) pp. 1–34 |
| [a12] | J. Robinson, "On the decision problem for algebraic rings" , Studies Math. Anal. Rel. Topics , Stanford Univ. Press (1962) pp. 297–304. |
Local-global principles for large rings of algebraic integers. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Local-global_principles_for_large_rings_of_algebraic_integers&oldid=39972