2020 Mathematics Subject Classification: Primary: 33C10 [MSN][ZBL]
Also generally called Bessel functions. Solutions $Z_\nu$ of the Bessel differential equation
\begin{equation}\label{e:Bessel}
z^2 \frac{d^2 Z}{dz^2} + z \frac{dZ}{dz} + (z^2-\nu^2) Z = 0
\end{equation}
where $\nu$ is an arbitrary real or complex number. The cylinder functions are functions of one complex variable.
Cylinder functions of arbitrary order.
If $\nu$ is not an integer, then the general solution of equation \eqref{e:Bessel} has the form
\[
c_1 J_\nu + c_{-1} J_{-\nu}
\]
where $J_{\pm \nu}$ are the so-called cylinder functions of the first kind or Bessel functions of the first kind. They have the expansion
\begin{equation}\label{e:Bessel_f}
J_\nu (z) = \left(\frac{z}{2}\right)^\nu \sum_{m=0}^\infty \frac{(-1)^m}{m! \Gamma (\nu +m +1)} \left(\frac{z}{2}\right)^{2m} \, ,
\end{equation}
where $\Gamma$ is the Gamma-function (i.e. the standard extension of the factorial to a meromorphic function on $\mathbb C$) and $z^\nu$ is given by ${\rm exp}\, (\log z)$, with the convention of having chosen the determination of $\log z$ such that $-\pi < {\rm Im}\, (\log z) \leq \pi$.
The formula \eqref{e:Bessel_f} still makes sense when $\nu$ is a nonnegative integer. For $n\in \mathbb N$ the function $J_{-n}$ is defined to be $(-1)^n J_n$ (the Bessel functions of integer order are usually defined as the coefficients of the following Laurent series:
\[
\left. e^{\frac{z}{2} \left(t - \frac{1}{t}\right)} = \sum_{n=-\infty}^\infty t^n J_n (z) \qquad \right)\, .
\]
The series on the right-hand side of \eqref{e:Bessel_f} converges absolutely and uniformly on any compact subset of $\mathbb C$. The functions $J_\nu$ are holomorphic on $\mathbb C \setminus \{0\}$ (in fact they are entire functions when $\nu$ is an integer). $\infty$ is a singular point, in the sense of the theory of analytic functions.
If $\nu$ is an integer, then $J_{\pm \nu}$ are linearly dependent and the linear combinations of them no longer yield the general solutions of \eqref{e:Bessel}. Therefore, apart from cylinder functions of the first kind one introduces cylinder functions of the second kind, commonly called Bessel functions of the second kind (or Neumann functions, Weber functions, cf. Neumann functions):
\begin{equation}\label{e:Bessel_f2}
Y_\nu (z) = \frac{J_\nu (z) \cos \nu \pi - J_{-\nu} (z)}{\sin \nu \pi} \qquad \mbox{for}\; \nu\not\in \mathbb Z
\end{equation}
\[
Y_n (z) = \lim_{\nu\to n} Y_\nu (z) \qquad \mbox{for}\; n\in \mathbb Z\,
\]
Another, less common notation, for the Bessel functions of the second kind is $N_\nu$. By means of these functions the general solution of equation \eqref{e:Bessel} can be written in the form
\[
Z_\nu = c_1 J_\nu + c_2 Y_\nu\, .
\]
For applications, a third class of solutions of \eqref{e:Bessel}, called cylinder functions of the third kind or Hankel functions are rather important They are denoted by $H^{(1)}_\nu$ and $H^{(2)}_\nu$ and defined as
\begin{align}
&H^{(1)}_\nu = J_\nu + i Y_\nu\\
&H^{(2)}_\nu = J_\nu - i Y_\nu\\
\end{align}
In particular, when $\nu\not\in \mathbb Z$, we have the expressions
\begin{align}
&H^{(1)}_\nu (z) = \frac{J_{-\nu} (z) - e^{-\nu \pi i} J_\nu (z)}{i\sin \nu\pi}\\
&H^{(2)}_\nu (z) = \frac{J_{-\nu} (z) - e^{\nu \pi i} J_\nu (z)}{-i\sin \nu\pi i}\, ,
\end{align}
whereas for integer values $n$ of $\nu$ analogous formulas hold if we replace the right hand sides with their limits as $\nu\to n$. When $\nu\in \mathbb R$, if we restrict the domain of the Hankel functions to the real axis, we get a pair of complex conjugate solutions of \eqref{e:Bessel}, of which the functions $J_\nu$ give the real part and the functions $Y_\nu$ give the imaginary part.
Each pair of functions $\{J_\nu, J_{-\nu}\}$, $\{Y_\nu, Y_{-\nu}\}$ and $\{H^{(1)}_\nu, H^{(2)}_\nu\}$ forms, when $\nu\not\in \mathbb Z$, a fundamental system of solutions of \eqref{e:Bessel}. The pairs $\{J_\nu, Y_\nu\}$ and $\{H^{(1)}_\nu, H^{(2)}_\nu\}$ form each a fundamental system of solutions for every value of $\nu$.
Some notable identities
We have the following important identities relating cylinder functions with their derivatives
\begin{align}
& \pi\, z \left( J_\nu (z) J'_{-\nu} (z) - J'_\nu (z) J_{-\nu} (z)\right) = - 2 \sin \nu\pi\\
& \pi\, z \left( J_\nu (z) Y'_{\nu} (z) - J'_\nu (z) Y_{\nu} (z)\right) = -2\\
& \pi\, z \left( H^{(1)}_\nu (z) (H^{(2)}_\nu)' (z)- (H^{(1)}_\nu)' (z) H^{(2)}_{\nu} (z) \right) = -4i
\end{align}
Similar formulas hold for expressions of the form $J_\nu Y''_\nu - J''_\nu Y_\nu$, $J'_\nu Y''_\nu - J''_\nu Y'_\nu$ and so on (see Section 3.63 of [Wa]).
Moreover, all cylinder functions $Z_\nu$ satisfy the recurrence formulas
\begin{align}
&z Z_{\nu-1} (z) + z Z_{\nu+1} (z) = 2\nu Z_\nu (z)\\
& Z_{\nu-1} (z) - Z_{\nu+1} (z) = 2 Z'_\nu (z)\, .
\end{align}
Modified cylinder functions
Modified cylinder functions are cylinder functions of an imaginary argument. For instance the function $I_\nu$ is defined as
\[
I_\nu (z) = \left\{\begin{array}{l}
&e^{-\frac{1}{2}\nu \pi i} J_\nu \left(z e^{\frac{1}{2}\pi i}\right) \qquad \mbox{if } -\pi < {\rm arg}\, z \leq \frac{\pi}{2}\\
&e^{\frac{3}{2}\nu \pi i} J_\nu \left(z e^{-\frac{3}{2}\pi i}\right) \qquad \mbox{if } \frac{\pi}{2} < {\rm arg}\, z \leq \pi
\end{array}\right.
\]
and the Macdonald function $K_\nu$ as
\[
K_\nu (z) = \frac{\pi i}{2} e^{\frac{1}{2}\nu \pi i} H^{(1)}_\nu (iz) = \frac{\pi i}{2} e^{-\frac{1}{2}\nu \pi i} H^{(1)}_{-\nu} (iz)
\]
(in particular observe that $K_{-\nu} = K_\nu$).
Obviously these functions are solutions of the differential equation
\[
z^2 \frac{d^2 Z}{dz^2} + z \frac{dZ}{dz} - (\nu^2 + z^2) Z = 0
\]
and in fact $\{I_\nu, K_\nu\}$ forms a fundamental system of solutions (similar to what happens for the usual cylinder functions,
the pair $\{I_\nu, I_{-\nu}\}$ forms a fundamental system only when $\nu$ is not an integer).
Moreover, the modified cylinder functions satisfy the recurrence relation
\begin{align}
&z (I_{\nu-1} (z) + I_{\nu+1} (z)) = 2 \nu I_\nu (z)\\
&z (K_{\nu-1} (z) + K_{\nu+1} (z)) = 2 \nu K_\nu (z)\, .
\end{align}
Cylinder functions of integral and half-integral orders.
If  is an integer,
is an integer, 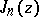 can be defined by means of the Jacobi–Anger formulas
can be defined by means of the Jacobi–Anger formulas
or
The equalities
hold. The function 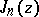 is an entire transcendental function of the argument
is an entire transcendental function of the argument  ; when
; when  ,
, 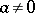 , is algebraic,
, is algebraic, 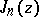 is a transcendental number, and
is a transcendental number, and 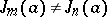 for
for 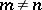 . As a second solution of (1), linearly independent of
. As a second solution of (1), linearly independent of 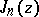 , one takes, as a rule, the function
, one takes, as a rule, the function
 | (8) |
where  is Euler's constant. If in one of the finite sums the upper summation index is less than the lower one, the corresponding sum has the value 0. The equality
is Euler's constant. If in one of the finite sums the upper summation index is less than the lower one, the corresponding sum has the value 0. The equality
holds.
Cylinder functions turn into elementary functions if and only if the index  takes the values
takes the values 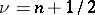 ,
, 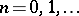 (spherical Bessel functions or cylinder functions of half-integral order). The following formulas hold
(spherical Bessel functions or cylinder functions of half-integral order). The following formulas hold 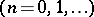 :
:
in particular, 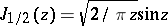 ;
;
in particular, 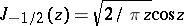 ;
;
Integral representations of cylinder functions.
When 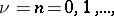 there are Bessel's integral representations
there are Bessel's integral representations
and
For 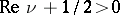 and
and 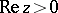 there are Poisson's integral representations
there are Poisson's integral representations
and
Apart from these there are many other integral representations, in particular in the form of contour integrals (see [2], [4], [5]).
Asymptotic behaviour of cylinder functions.
For 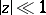 ,
, 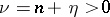 ,
, 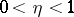 , one has
, one has
For real  ,
,
For 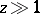 ,
, 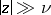 there is the following estimate
there is the following estimate
 | (9) |
 | (10) |
For 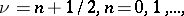 the series (9) and (10) terminate. The Hankel functions are the only cylinder functions that tend to 0 for complex values of the variable
the series (9) and (10) terminate. The Hankel functions are the only cylinder functions that tend to 0 for complex values of the variable  as
as 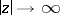 (and this is their merit in applications):
(and this is their merit in applications):
For large values of 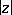 and
and 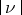 asymptotic series of special types are used (see [1], [2], [3], [5]).
asymptotic series of special types are used (see [1], [2], [3], [5]).
Zeros of cylinder functions.
The zeros of an arbitrary cylinder function are simple except for 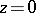 . If
. If 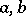 and
and  are real, then between two real zeros of
are real, then between two real zeros of 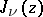 lies one real zero of
lies one real zero of 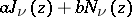 . For real
. For real  ,
, 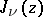 has infinitely many real zeros; for
has infinitely many real zeros; for 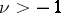 all zeros of
all zeros of 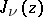 are real; if
are real; if 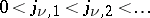 are the positive zeros of
are the positive zeros of  , then
, then
For 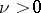 ,
, 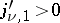 for the smallest positive zero of
for the smallest positive zero of 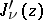 . The pairs of functions
. The pairs of functions 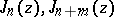 ;
; 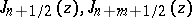 ,
, 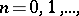
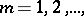 have no common zeros except
have no common zeros except 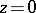 . If
. If
then 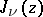 has exactly
has exactly 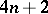 complex zeros, two of which are pure imaginary; if
complex zeros, two of which are pure imaginary; if 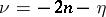 ,
, 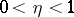 ,
, 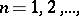 then
then 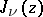 has exactly
has exactly 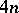 complex zeros with non-zero real part.
complex zeros with non-zero real part.
Addition theorems and series expansions of cylinder functions.
The following addition theorems hold:
where
and
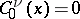 are the ultraspherical polynomials. In expansions of cylinder functions one uses Lommel polynomials (cf. Lommel polynomial), Neumann series, Fourier–Bessel series, and Dirichlet series.
are the ultraspherical polynomials. In expansions of cylinder functions one uses Lommel polynomials (cf. Lommel polynomial), Neumann series, Fourier–Bessel series, and Dirichlet series.
Connected with spherical functions are the Anger functions, the Struve functions, the Lommel functions (cf. Anger function; Struve function; Lommel function), as well as the Kelvin functions and the Airy functions.
Cylinder functions can be defined as limit functions of spherical functions in the following way:
Here, asymptotic representations of spherical functions are connected with cylinder functions and vice versa, for example, as in Hilb's formula
and in the expansions of Macdonald, Watson, Tricomi, and others (see [1], [2], [4]).
Calculation of values of cylinder functions on a computer.
For the numerical evaluation of the functions 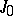 ,
, 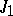 ,
, 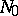 ,
,  ,
, 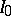 ,
, 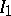 ,
, 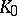 ,
, 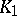 , approximations by polynomials and rational functions are convenient (see [5]). For expansions with respect to Chebyshev polynomials see [6]. For the calculation of functions of large integral order, especially on a computer, one uses the recurrence relations (5)–(7) (see [5]).
, approximations by polynomials and rational functions are convenient (see [5]). For expansions with respect to Chebyshev polynomials see [6]. For the calculation of functions of large integral order, especially on a computer, one uses the recurrence relations (5)–(7) (see [5]).
Information on tables of cylinder functions can be found in [7], [8], [9].
References
| [1] | G.N. Watson, "A treatise on the theory of Bessel functions" , 1 , Cambridge Univ. Press (1952) |
| [2] | H. Bateman (ed.) A. Erdélyi (ed.) et al. (ed.) , Higher transcendental functions , 2. Bessel functions, parabolic cylinder functions, orthogonal polynomials , McGraw-Hill (1953) |
| [3] | N.N. Lebedev, "Special functions and their applications" , Prentice-Hall (1965) (Translated from Russian) |
| [4] | I.S. Gradshtein, I.M. Ryzhik, "Table of integrals, series and products" , Acad. Press (1980) (Translated from Russian) |
| [5] | M. Abramowitz, I.A. Stegun, "Handbook of mathematical functions" , Dover, reprint (1973) pp. Chapts. 9–11 |
| [6] | C.W. Clenshaw, "Chebyshev series for mathematical functions" , Math. Tables , 5 , Cambridge Univ. Press (1962) |
| [7] | A.L. Lebedev, R.M. Fedorova, "Handbook of mathematical tables" , Moscow (1956) (In Russian) |
| [8] | N.M. Burunova, "Mathematical tables" , Moscow (1959) (In Russian) (Completion no. 1) |
| [9] | A.A. Fletcher, J.C.P. Miller, L. Rosenhead, L.J. Comrie, "An index of mathematical tables" , 1–2 , Oxford Univ. Press (1962) |
Tables.
References
| [1] | E.A. Chistova, "Tables of Bessel functions of a real argument and their integrals" , Moscow (1958) (In Russian) |
| [2] | L.N. Karmazina, E.A. Chistova, "Tables of Bessel functions of an imaginary argument and their integrals" , Moscow (1958) (In Russian) |
| [3] | , Tables of Bessel functions of fractional order , 1–2 , Nat. Bur. Standards (1948–1949) |
| [4] | H.K. Crowder, G.C. Francis, "Tables of spherical Bessel functions and ordinary Bessel functions of order half and odd integer of the first and second kind" , Ballistic Res. Lab. Mem. Rep. 1027 (1956) |
| [5] | , Tables of spherical Bessel functions , 1–2 , Nat. Bur. Standards (1947) |
| [6] | , Tables of the Bessel functions 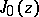 and and 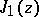 for complex arguments , Nat. Bur. Standards (1947) for complex arguments , Nat. Bur. Standards (1947) |
| [7] | , Tables of the Bessel functions 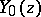 and and 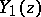 for complex arguments , Nat. Bur. Standards (1950) for complex arguments , Nat. Bur. Standards (1950) |
| [8] | , Bessel functions III. Zeros and associated values , Roy. Soc. Math. Tables , 7 , Cambridge Univ. Press (1960) |
 is an integer,
is an integer, 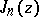 can be defined by means of the Jacobi–Anger formulas
can be defined by means of the Jacobi–Anger formulas
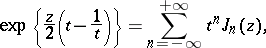
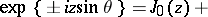
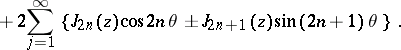
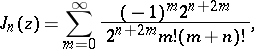
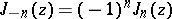
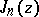 is an entire transcendental function of the argument
is an entire transcendental function of the argument  ; when
; when  ,
, 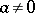 , is algebraic,
, is algebraic, 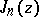 is a transcendental number, and
is a transcendental number, and 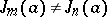 for
for 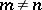 . As a second solution of (1), linearly independent of
. As a second solution of (1), linearly independent of 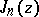 , one takes, as a rule, the function
, one takes, as a rule, the function

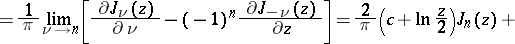
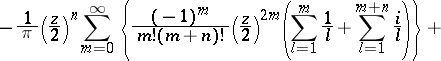
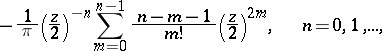
 is Euler's constant. If in one of the finite sums the upper summation index is less than the lower one, the corresponding sum has the value 0. The equality
is Euler's constant. If in one of the finite sums the upper summation index is less than the lower one, the corresponding sum has the value 0. The equality
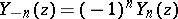
 takes the values
takes the values 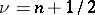 ,
, 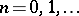 (spherical Bessel functions or cylinder functions of half-integral order). The following formulas hold
(spherical Bessel functions or cylinder functions of half-integral order). The following formulas hold 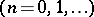 :
:
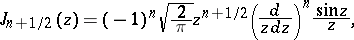
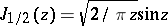 ;
;
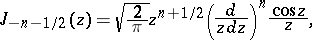
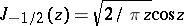 ;
;
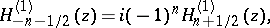
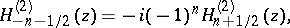
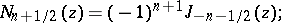
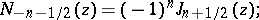
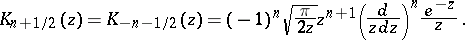
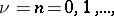 there are Bessel's integral representations
there are Bessel's integral representations
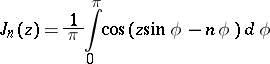
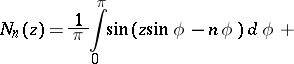

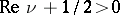 and
and 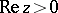 there are Poisson's integral representations
there are Poisson's integral representations
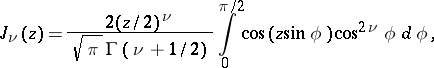
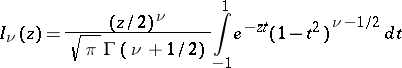
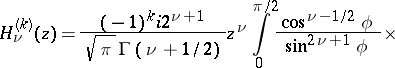
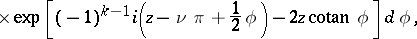
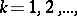
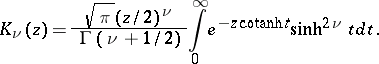
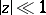 ,
, 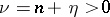 ,
, 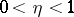 , one has
, one has
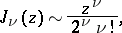
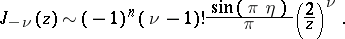
 ,
,
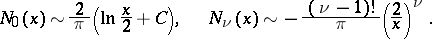
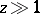 ,
, 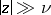 there is the following estimate
there is the following estimate
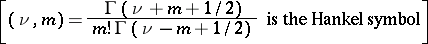
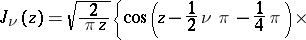
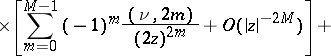
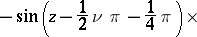
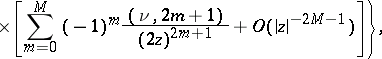
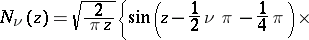
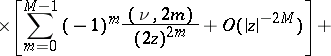
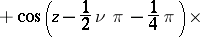
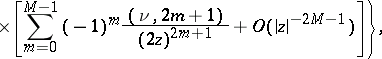
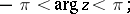

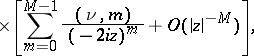
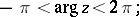

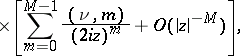
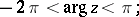
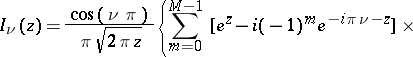
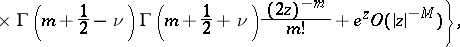

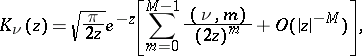
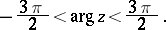
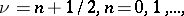 the series (9) and (10) terminate. The Hankel functions are the only cylinder functions that tend to 0 for complex values of the variable
the series (9) and (10) terminate. The Hankel functions are the only cylinder functions that tend to 0 for complex values of the variable  as
as 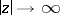 (and this is their merit in applications):
(and this is their merit in applications):
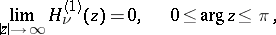
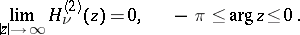
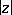 and
and 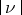 asymptotic series of special types are used (see [1], [2], [3], [5]).
asymptotic series of special types are used (see [1], [2], [3], [5]).
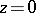 . If
. If 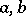 and
and  are real, then between two real zeros of
are real, then between two real zeros of 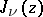 lies one real zero of
lies one real zero of 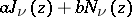 . For real
. For real  ,
, 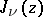 has infinitely many real zeros; for
has infinitely many real zeros; for 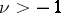 all zeros of
all zeros of 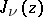 are real; if
are real; if 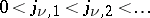 are the positive zeros of
are the positive zeros of  , then
, then

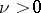 ,
, 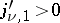 for the smallest positive zero of
for the smallest positive zero of 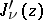 . The pairs of functions
. The pairs of functions 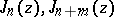 ;
; 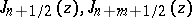 ,
, 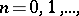
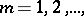 have no common zeros except
have no common zeros except 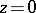 . If
. If
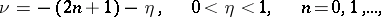
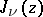 has exactly
has exactly 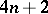 complex zeros, two of which are pure imaginary; if
complex zeros, two of which are pure imaginary; if 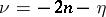 ,
, 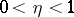 ,
, 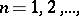 then
then 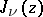 has exactly
has exactly 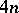 complex zeros with non-zero real part.
complex zeros with non-zero real part.
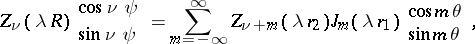
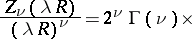
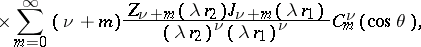
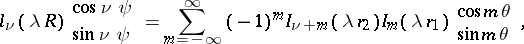
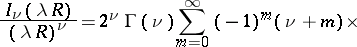
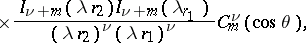
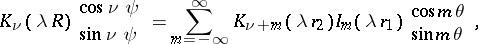
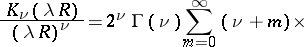
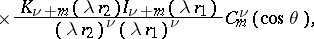
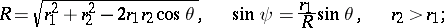

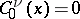 are the ultraspherical polynomials. In expansions of cylinder functions one uses Lommel polynomials (cf. Lommel polynomial), Neumann series, Fourier–Bessel series, and Dirichlet series.
are the ultraspherical polynomials. In expansions of cylinder functions one uses Lommel polynomials (cf. Lommel polynomial), Neumann series, Fourier–Bessel series, and Dirichlet series.
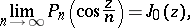
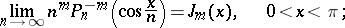
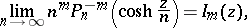
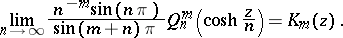
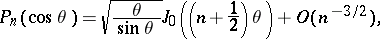
 ,
, 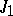 ,
, 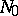 ,
,  ,
, 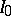 ,
, 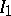 ,
, 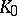 ,
, 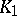 , approximations by polynomials and rational functions are convenient (see [5]). For expansions with respect to Chebyshev polynomials see [6]. For the calculation of functions of large integral order, especially on a computer, one uses the recurrence relations (5)–(7) (see [5]).
, approximations by polynomials and rational functions are convenient (see [5]). For expansions with respect to Chebyshev polynomials see [6]. For the calculation of functions of large integral order, especially on a computer, one uses the recurrence relations (5)–(7) (see [5]).
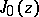 and
and 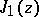 for complex arguments , Nat. Bur. Standards (1947)
for complex arguments , Nat. Bur. Standards (1947)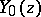 and
and 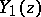 for complex arguments , Nat. Bur. Standards (1950)
for complex arguments , Nat. Bur. Standards (1950)