Neumann function

2020 Mathematics Subject Classification: Primary: 33C10 [MSN][ZBL]

More commonly called Bessel function, or Cylinder function, of the second kind. They were introduced by Neumann in 1867 (and hence the terminology Neumann functions used by some authors). The Bessel functions of the second type $Y_\nu$ (occasionally the notation $N_\nu$ is also used) can be defined in terms of the Bessel functions of the first kind $J_\nu$ as follows: \begin{equation}\label{e:Bessel_f2} Y_\nu (z) = \frac{J_\nu (z) \cos \nu \pi - J_{-\nu} (z)}{\sin \nu \pi} \qquad \mbox{for}\; \nu\not\in \mathbb Z \end{equation} \[ Y_n (z) = \lim_{\nu\to n} Y_\nu (z) \qquad \mbox{for}\; n\in \mathbb Z\, \] where $\nu$ can be any complex number.

When $\nu = p$ real the function $Y_p$ takes real values on the positive real axis and tends to zero as $x\to\infty$. For large $x$ they have the asymptotic representation \[ Y_p (x) = \sqrt{\frac{2}{\pi x}} \sin \left(x - \frac{1}{2} p\pi - \frac{\pi}{4}\right) +O\left( \frac{1}{x^{3/2}}\right). \] They are connected by the recurrence formulas \begin{align*} &Y_{p-1} (x) + Y_{p+1} (x) = \frac{2p}{x} Y_p (x)\\ &Y_{p-1} (x) - Y_{p+1} (x) = 2 Y'_p (x)\, . \end{align*} For integers $p=n$ we have \[ Y_{-n} = (-1)^n Y_n\, . \] For $p=n$ natural number and small $x$ we have the asymptotic formulas \[ Y_0 (x) \sim -\frac{2}{\pi} \ln \left(\frac{2}{\gamma x}\right)\, , \qquad Y_n (x) \sim - \frac{(n-1)!}{\pi} \left(\frac{2}{x}\right)^n\, , \] where $\gamma$ is the Euler constant.

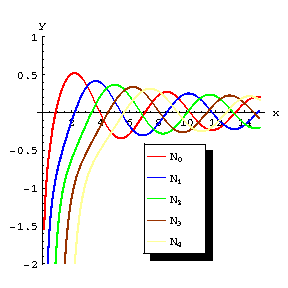
Figure: n066420a

Graphs of some Bessel functions of the second kind.

The Neumann functions of "half-integral" order $p = \frac{2n+1}{2}$ can be expressed in terms of the trigonometric functions; in particular, \[ Y_{1/2} (x) = - \sqrt{\frac{2}{\pi x}} \cos x\, , \qquad Y_{-1/2} (x) = \sqrt{\frac{2}{\pi x}} \sin x\, . \]

For further references see Cylinder functions.

References

• Harold Jeffreys, Bertha Jeffreys, Methods of Mathematical Physics, 3rd edition, Cambridge University Press (1972) Zbl 0238.00004