Drinfel'd module
A Drinfel'd 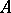 -module, (where
-module, (where 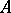 is an appropriate ring) over a field
is an appropriate ring) over a field 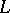 of characteristic
of characteristic 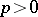 is an exotic
is an exotic  -module structure on the additive group
-module structure on the additive group 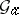 over
over  . In several regards, the concept of a Drinfel'd module is analogous to the concept of an elliptic curve (or more generally, of an irreducible Abelian variety), with which it shares many features. Among the similarities between Drinfel'd modules and elliptic curves are the respective structures of torsion points, of Tate modules and of endomorphism rings, the existence of analytic "Weierstrass uniformizations" , and the moduli theories (modular varieties, modular forms; cf. also Modular form). Many topics from the (classical and well-developed) theory of elliptic curves may be transferred to Drinfel'd modules, thereby revealing arithmetical information about the ground field
. In several regards, the concept of a Drinfel'd module is analogous to the concept of an elliptic curve (or more generally, of an irreducible Abelian variety), with which it shares many features. Among the similarities between Drinfel'd modules and elliptic curves are the respective structures of torsion points, of Tate modules and of endomorphism rings, the existence of analytic "Weierstrass uniformizations" , and the moduli theories (modular varieties, modular forms; cf. also Modular form). Many topics from the (classical and well-developed) theory of elliptic curves may be transferred to Drinfel'd modules, thereby revealing arithmetical information about the ground field 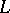 . On the other hand, since the mechanism of Drinfel'd modules is smoother and in some respects simpler than that of Abelian varieties, some results involving Drinfel'd modules over global function fields
. On the other hand, since the mechanism of Drinfel'd modules is smoother and in some respects simpler than that of Abelian varieties, some results involving Drinfel'd modules over global function fields 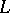 can be proved, whose analogues over number fields
can be proved, whose analogues over number fields 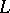 are far from being settled (e.g. parts of Stark's conjectures, of the Langlands conjectures, assertions about the arithmetical nature of zeta values and other questions of transcendence theory over
are far from being settled (e.g. parts of Stark's conjectures, of the Langlands conjectures, assertions about the arithmetical nature of zeta values and other questions of transcendence theory over 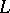 , cf. also
, cf. also 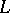 -function). The invention and basic theory as well as large parts of the deeper results about Drinfel'd modules are due to V.G. Drinfel'd [a3], [a4]. General references are [a2], [a10], [a9], and [a8].
-function). The invention and basic theory as well as large parts of the deeper results about Drinfel'd modules are due to V.G. Drinfel'd [a3], [a4]. General references are [a2], [a10], [a9], and [a8].
Algebraic theory.
Let 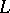 be any field of characteristic
be any field of characteristic 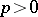 , with algebraic closure
, with algebraic closure  . The endomorphism ring
. The endomorphism ring 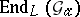 of the additive group scheme
of the additive group scheme 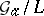 is the ring of additive polynomials
is the ring of additive polynomials 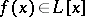 , i.e., of polynomials satisfying
, i.e., of polynomials satisfying 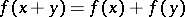 , whose (non-commutative) multiplication is defined by insertion. Then
, whose (non-commutative) multiplication is defined by insertion. Then
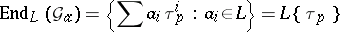 |
is the twisted polynomial ring in  with commutation rule
with commutation rule 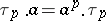 for
for 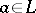 and unit element
and unit element 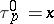 . Fix a power
. Fix a power 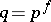 of
of 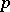 . If
. If 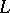 contains the field
contains the field  with
with 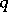 elements, one sets
elements, one sets 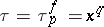 and
and 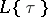 for the subring of
for the subring of 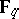 -linear polynomials in
-linear polynomials in 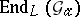 . For any
. For any 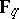 -algebra
-algebra  , an
, an 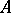 -module structure on
-module structure on  is given by a morphism
is given by a morphism 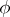 of
of  -algebras from
-algebras from 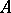 to
to 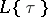 .
.
Fix a (smooth, projective, geometrically connected) algebraic curve 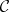 over
over 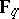 and a place "∞" of
and a place "∞" of 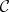 ; let
; let 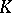 be its function field and
be its function field and 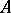 the affine ring of
the affine ring of 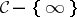 . (Here, "places" , or "primes" , are closed points of
. (Here, "places" , or "primes" , are closed points of  , the set of normalized valuations on
, the set of normalized valuations on 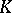 ; cf. also Norm on a field.) Hence
; cf. also Norm on a field.) Hence 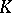 is a function field in one variable over
is a function field in one variable over 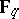 and
and 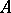 is its subring of elements regular away from
is its subring of elements regular away from 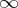 . Put
. Put  for the associated degree function:
for the associated degree function: 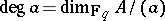 if
if 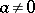 . Let
. Let 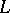 be a field equipped with a structure
be a field equipped with a structure 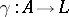 of an
of an 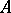 -algebra. Then
-algebra. Then 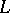 is either an extension of
is either an extension of 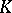 or of some
or of some 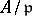 , where
, where 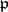 is a maximal ideal. One writes
is a maximal ideal. One writes 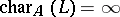 in the former and
in the former and 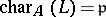 in the latter case. A Drinfel'd
in the latter case. A Drinfel'd 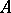 -module of rank
-module of rank  over
over 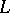 (briefly, an
(briefly, an  -Drinfel'd module over
-Drinfel'd module over 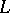 ) is a morphism of
) is a morphism of 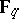 -algebras
-algebras
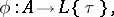 |
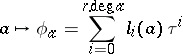 |
subject to:
i)  ; and
; and
ii)  for
for 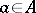 . It supplies the additive group
. It supplies the additive group  of each
of each 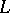 -algebra
-algebra 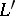 with the structure of an abstract
with the structure of an abstract  -module. A morphism
-module. A morphism 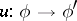 of Drinfel'd
of Drinfel'd 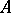 -modules over
-modules over 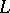 is some element
is some element  of
of 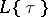 that satisfies
that satisfies 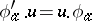 for
for 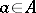 . Similarly, one defines iso-, endo- and automorphisms.
. Similarly, one defines iso-, endo- and automorphisms.
The standard example of 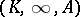 is given by a rational function field
is given by a rational function field 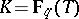 ,
, 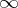 being the usual place at infinity,
being the usual place at infinity, 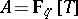 . In that case, a Drinfel'd
. In that case, a Drinfel'd 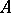 -module
-module 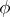 of rank
of rank  over
over 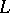 is given by
is given by  , where the
, where the 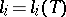 may be arbitrarily chosen in
may be arbitrarily chosen in 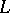 (
(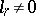 ). More generally, if
). More generally, if 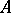 is generated over
is generated over 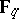 by
by 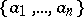 ,
, 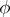 is given by the
is given by the 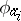 that in
that in 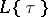 must satisfy the same relations as do the
must satisfy the same relations as do the 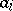 in
in 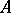 . Writing down a Drinfel'd module amounts to solving a complicated system of polynomial equations over
. Writing down a Drinfel'd module amounts to solving a complicated system of polynomial equations over 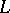 . For example, let
. For example, let 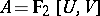 with
with 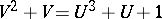 . From
. From 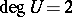 ,
, 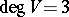 , one obtains for a
, one obtains for a  -Drinfel'd module
-Drinfel'd module 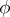 over
over  :
:  with
with 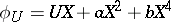 ,
, 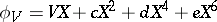 . Using computation rules in
. Using computation rules in 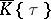 , one solves for
, one solves for 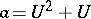 ,
, 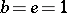 ,
, 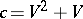 ,
, 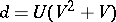 , which yields the unique (up to isomorphism)
, which yields the unique (up to isomorphism) 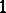 -Drinfel'd module
-Drinfel'd module 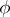 over
over 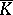 . That
. That 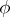 is unique and even definable over
is unique and even definable over 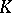 corresponds to the fact that the class number of
corresponds to the fact that the class number of 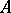 equals
equals 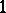 .
.
Let 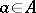 with
with 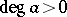 and let
and let 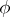 be an
be an  -Drinfel'd module over
-Drinfel'd module over 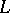 . The polynomial
. The polynomial 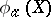 has degree
has degree 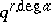 in
in 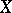 , whence has
, whence has 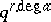 different roots in
different roots in 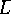 if
if  . This implies that the
. This implies that the 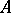 -module of
-module of  -torsion points
-torsion points  of
of 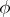 is isomorphic with
is isomorphic with 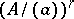 . Similar, but more complicated assertions hold if one considers
. Similar, but more complicated assertions hold if one considers  -torsion points (
-torsion points ( a not necessarily principal ideal of
a not necessarily principal ideal of 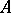 ) and if
) and if 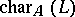 divides
divides  . A level-
. A level- structure on
structure on 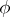 is the choice of an isomorphism
is the choice of an isomorphism 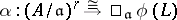 of abstract
of abstract 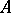 -modules (with some modification if
-modules (with some modification if 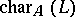 divides
divides  ).
).
The definitions of Drinfel'd modules, their morphisms, torsion points, and level structures generalize to arbitrary 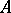 -schemes
-schemes 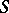 (instead of
(instead of 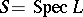 , which corresponds to the case above; cf. also Scheme). Intuitively, an
, which corresponds to the case above; cf. also Scheme). Intuitively, an  -Drinfel'd module over
-Drinfel'd module over 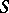 is a family of
is a family of  -Drinfel'd modules varying continuously over
-Drinfel'd modules varying continuously over 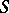 . Let
. Let 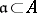 be a non-vanishing ideal. On the category of
be a non-vanishing ideal. On the category of 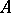 -schemes
-schemes 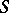 , there is the contravariant functor
, there is the contravariant functor 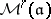 that to each
that to each 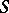 associates the set of isomorphism classes of
associates the set of isomorphism classes of  -Drinfel'd modules over
-Drinfel'd modules over 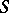 provided with a level-
provided with a level- structure. If
structure. If  has at least two prime divisors (such
has at least two prime divisors (such  are admissible),
are admissible), 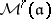 is representable by a moduli scheme
is representable by a moduli scheme  . In other words,
. In other words, 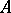 -morphisms from
-morphisms from 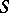 to
to 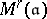 correspond one-to-one to isomorphism classes of
correspond one-to-one to isomorphism classes of  -Drinfel'd modules over
-Drinfel'd modules over 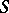 with a level-
with a level- structure. The various
structure. The various 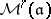 and
and 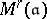 are equipped with actions of the finite groups
are equipped with actions of the finite groups 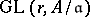 and related by morphisms
and related by morphisms  if
if 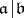 . Taking quotients, this allows one to define coarse moduli schemes
. Taking quotients, this allows one to define coarse moduli schemes  even for non-admissible ideals
even for non-admissible ideals  , and for more general moduli problems, e.g., the problem "rank-r Drinfel'd A-modules with a point of order a A" . For such coarse moduli schemes, the above bijection between morphisms from
, and for more general moduli problems, e.g., the problem "rank-r Drinfel'd A-modules with a point of order a A" . For such coarse moduli schemes, the above bijection between morphisms from 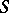 to
to  and objects of the moduli problem holds only if
and objects of the moduli problem holds only if 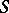 is the spectrum of an algebraically closed field. If
is the spectrum of an algebraically closed field. If  is admissible,
is admissible, 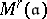 is affine, smooth, of finite type and of dimension
is affine, smooth, of finite type and of dimension 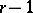 over
over 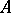 . Furthermore, for
. Furthermore, for 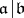 , the morphisms from
, the morphisms from 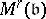 to
to 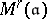 are finite and flat, and even étale outside the support of
are finite and flat, and even étale outside the support of 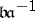 (cf. also Affine morphism; Flat morphism; Etale morphism). As an example, take
(cf. also Affine morphism; Flat morphism; Etale morphism). As an example, take 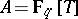 , and let
, and let  be algebraically closed. Two
be algebraically closed. Two  -Drinfel'd modules
-Drinfel'd modules  and
and 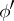 over
over  , given through the coefficients
, given through the coefficients  and
and 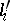 (
(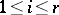 ) of
) of 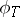 and
and 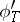 , are isomorphic if and only if there exists a
, are isomorphic if and only if there exists a  such that
such that 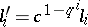 . Hence
. Hence 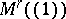 , the moduli scheme attached to the trivial ideal
, the moduli scheme attached to the trivial ideal 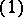 of
of 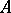 , is the open subscheme defined by
, is the open subscheme defined by 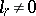 of
of 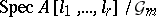 , where the multiplicative group acts diagonally through
, where the multiplicative group acts diagonally through 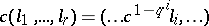 . If
. If  ,
, 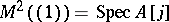 with the "modular invariant"
with the "modular invariant"  , the
, the 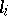 being regarded as indeterminates.
being regarded as indeterminates.
Analytic theory.
Let 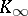 be the completion of
be the completion of 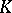 at
at 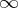 , with normalized absolute value
, with normalized absolute value 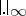 and complete algebraic closure
and complete algebraic closure  . Then
. Then 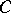 is the smallest field extension of
is the smallest field extension of 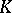 which is complete with respect to
which is complete with respect to 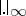 and algebraically closed. For such fields, there is a reasonable function theory and analytic geometry [a1].
and algebraically closed. For such fields, there is a reasonable function theory and analytic geometry [a1].
An 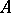 -lattice is a finitely generated (thus projective)
-lattice is a finitely generated (thus projective) 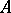 -submodule
-submodule 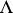 of
of 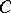 that has finite intersection with each ball in
that has finite intersection with each ball in 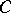 . With
. With 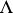 is associated its exponential function
is associated its exponential function 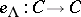 , defined as the everywhere convergent infinite product
, defined as the everywhere convergent infinite product 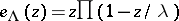 (
(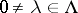 ). It is a surjective,
). It is a surjective, 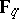 -linear and
-linear and 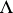 -periodic function that for each
-periodic function that for each 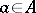 satisfies a functional equation
satisfies a functional equation 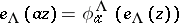 with some
with some 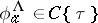 . The rule
. The rule 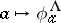 defines a ring homomorphism from
defines a ring homomorphism from 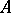 to
to 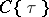 , in fact, a Drinfel'd
, in fact, a Drinfel'd 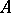 -module of rank
-module of rank  ,
,  being the projective rank of the
being the projective rank of the 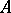 -module
-module 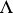 . Each
. Each  -Drinfel'd module over
-Drinfel'd module over 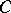 is so obtained, and
is so obtained, and 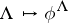 yields an equivalence of the category of lattices of projective rank
yields an equivalence of the category of lattices of projective rank  with the category of
with the category of  -Drinfel'd modules over
-Drinfel'd modules over 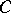 . (A morphism of lattices
. (A morphism of lattices 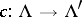 is some
is some 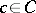 such that
such that 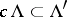 .) The description of
.) The description of 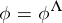 through the lattice
through the lattice  is called the Weierstrass uniformization. From
is called the Weierstrass uniformization. From 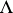 , one can read off many of the properties of
, one can read off many of the properties of 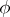 . E.g.,
. E.g.,
 |
and  (
(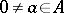 ). For
). For 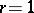 , there result bijections between the finite sets of:
, there result bijections between the finite sets of:
a) classes of rank-one 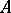 -lattices in
-lattices in 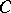 , up to scalars;
, up to scalars;
b) ideal classes of 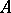 , i.e.,
, i.e., 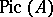 ;
;
c) isomorphism classes of rank-one Drinfel'd modules over  , i.e.,
, i.e., 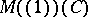 . For
. For 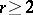 , let
, let 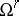 be the analytic subspace
be the analytic subspace
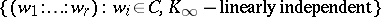 |
of 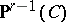 . Note that
. Note that 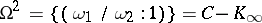 , which is the Drinfel'd upper half-plane. The set (in fact,
, which is the Drinfel'd upper half-plane. The set (in fact, 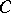 -analytic space) of
-analytic space) of 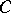 -valued points of the moduli scheme
-valued points of the moduli scheme 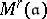 may now be described as a finite union
may now be described as a finite union 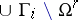 of quotients of
of quotients of 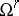 by subgroups
by subgroups 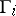 of
of 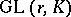 commensurable with
commensurable with 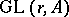 , in much the same way as one usually describes the moduli of elliptic curves over
, in much the same way as one usually describes the moduli of elliptic curves over 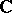 . In the standard example
. In the standard example 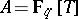 ,
, 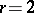 ,
, 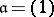 , one obtains the
, one obtains the 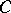 -analytic isomorphisms
-analytic isomorphisms 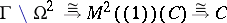 , where
, where 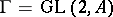 . The left-hand mapping associates with
. The left-hand mapping associates with 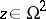 the Drinfel'd module
the Drinfel'd module 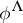 with
with 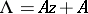 , and the right-hand mapping is given by the modular invariant
, and the right-hand mapping is given by the modular invariant 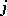 . Writing
. Writing 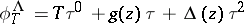 , the coefficients
, the coefficients 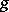 and
and 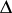 become functions in
become functions in 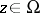 , in fact, modular forms for
, in fact, modular forms for 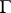 of respective weights
of respective weights 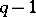 and
and 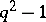 . Moduli problems with non-trivial level structures correspond to subgroups
. Moduli problems with non-trivial level structures correspond to subgroups 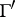 of
of 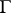 , i.e., to modular curves
, i.e., to modular curves  , which are ramified covers of the above. As "classically" these curves may be studied function-theoretically via the modular forms for
, which are ramified covers of the above. As "classically" these curves may be studied function-theoretically via the modular forms for 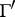 . The same holds, more or less, for more general base rings than
. The same holds, more or less, for more general base rings than 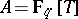 and for higher ranks
and for higher ranks  than
than 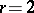 . Quite generally, the moduli schemes
. Quite generally, the moduli schemes 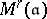 encode essential parts of the arithmetic of
encode essential parts of the arithmetic of 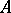 and
and 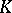 , as will be demonstrated by the examples below.
, as will be demonstrated by the examples below.
Applications.
Explicit Abelian class field theory of 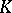 .
.
Adjoining torsion points of rank-one Drinfel'd modules results in Abelian extensions of the base field. Applying this to the 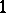 -Drinfel'd module
-Drinfel'd module 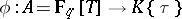 defined by
defined by 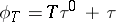 (the so-called Carlitz module) yields all the Abelian extensions of
(the so-called Carlitz module) yields all the Abelian extensions of 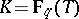 that are tamely ramified at
that are tamely ramified at 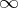 , similar to cyclotomic extensions of the field
, similar to cyclotomic extensions of the field 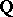 of rationals. This also works for general base rings
of rationals. This also works for general base rings 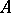 with class numbers
with class numbers 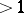 ; here the situation resembles the theory of complex multiplication of elliptic curves [a11] (cf. also Elliptic curve).
; here the situation resembles the theory of complex multiplication of elliptic curves [a11] (cf. also Elliptic curve).
Langlands conjectures in characteristic 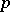 .
.
The moduli scheme 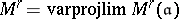 is equipped with an action of
is equipped with an action of 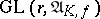 (where
(where  is the ring of finite adèles of
is the ring of finite adèles of  ). It is a major problem to determine the representation type of the
). It is a major problem to determine the representation type of the  -adic cohomology modules
-adic cohomology modules 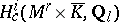 , i.e., to express them in terms of automorphic representations. This can partially be achieved and leads to (local or global) reciprocity laws between representations of
, i.e., to express them in terms of automorphic representations. This can partially be achieved and leads to (local or global) reciprocity laws between representations of 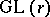 and Galois representations (cf. also Galois theory). In particular, the local Langlands correspondence for
and Galois representations (cf. also Galois theory). In particular, the local Langlands correspondence for  over a local field of equal characteristic may so be proved [a4], [a13], [a12].
over a local field of equal characteristic may so be proved [a4], [a13], [a12].
Modularity conjecture over  .
.
As a special case of the previous subsection, the Galois representations associated to elliptic curves over 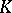 may be found in
may be found in 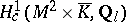 . This leads to a Shimura–Taniyama–Weil correspondence between elliptic curves over
. This leads to a Shimura–Taniyama–Weil correspondence between elliptic curves over 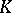 with split multiplicative reduction at
with split multiplicative reduction at 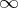 , isogeny factors of dimension one of Jacobians of certain Drinfel'd modular curves and (effectively calculable) automorphic Hecke eigenforms over
, isogeny factors of dimension one of Jacobians of certain Drinfel'd modular curves and (effectively calculable) automorphic Hecke eigenforms over 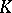 [a7].
[a7].
Cohomology of arithmetic groups.
Invariants like Betti numbers, numbers of cusps, Euler–Poincaré-characteristics of subgroups  of
of 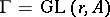 are related to the geometry of the moduli scheme
are related to the geometry of the moduli scheme  . In some cases (e.g.,
. In some cases (e.g., 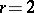 ), these invariants may be determined using the theory of Drinfel'd modular forms [a5].
), these invariants may be determined using the theory of Drinfel'd modular forms [a5].
Arithmetic of division algebras.
Exploiting the structure of endomorphism rings of Drinfel'd modules over finite 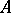 -fields and using knowledge of the moduli schemes, one can find formulas for class and type numbers of central division algebras over
-fields and using knowledge of the moduli schemes, one can find formulas for class and type numbers of central division algebras over 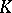 [a6].
[a6].
Curves with many rational points.
Drinfel'd modules provide explicit constructions of algebraic curves over finite fields with predictable properties. In particular, curves with many rational points compared to their genera may be tailored [a14].
Other features and deep results in the field that definitely should be mentioned are the following:
the transcendence theory of Drinfel'd modules, their periods, and special values of exponential lattice functions, mainly created by J. Yu [a17];
D. Goss has developed a theory of 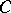 -valued zeta- and
-valued zeta- and 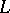 -functions for Drinfel'd modules and similar objects [a9];
-functions for Drinfel'd modules and similar objects [a9];
R. Pink has proved an analogue of the Tate conjecture (cf. also Tate conjectures) for Drinfel'd modules [a15];
H.-G. Rück and U. Tipp have proved a Gross–Zagier-type formula for heights of Heegner points on Drinfel'd modular curves [a16].
References
| [a1] | S. Bosch, U. Güntzer, R. Remmert, "Non-Archimedean analysis" , Springer (1984) MR0746961 Zbl 0539.14017 |
| [a2] | P. Deligne, D. Husemöller, "Survey of Drinfel'd modules" Contemp. Math. , 67 (1987) pp. 25–91 MR902591 Zbl 0627.14026 |
| [a3] | V.G. Drinfel'd, "Elliptic modules" Math. USSR Sb. , 23 (1976) pp. 561–592 Zbl 0386.20022 Zbl 0363.20038 Zbl 0321.14014 |
| [a4] | V.G. Drinfel'd, "Elliptic modules II" Math. USSR Sb. , 31 (1977) pp. 159–170 Zbl 0386.20022 Zbl 0363.20038 |
| [a5] | E.-U. Gekeler, "Drinfeld modular curves" , Lecture Notes Math. , 1231 , Springer (1986) MR0874338 MR0827352 Zbl 0607.14020 Zbl 0599.14032 |
| [a6] | E.-U. Gekeler, "On the arithmetic of some division algebras" Comment. Math. Helvetici , 67 (1992) pp. 316–333 MR1161288 Zbl 0753.11025 |
| [a7] | E.-U. Gekeler, M. Reversat, "Jacobians of Drinfeld modular curves" J. Reine Angew. Math. , 476 (1996) pp. 27–93 MR1401696 Zbl 0848.11029 |
| [a8] | "Drinfeld modules, modular schemes and applications" E.-U. Gekeler (ed.) M. van der Put (ed.) M. Reversat (ed.) J. van Geel (ed.) , World Sci. (1997) MR1630594 Zbl 0897.00023 |
| [a9] | D. Goss, "Basic structures of function field arithmetic" , Springer (1996) MR1423131 Zbl 0874.11004 |
| [a10] | "The arithmetic of function fields" D. Goss (ed.) D. Hayes (ed.) M. Rosen (ed.) , W. de Gruyter (1992) MR1196508 Zbl 0771.00031 |
| [a11] | D. Hayes, "Explicit class field theory in global function fields" , Studies Algebra and Number Th. , Adv. Math. , 16 (1980) pp. 173–217 MR0535766 Zbl 0476.12010 |
| [a12] | G. Laumon, "Cohomology of Drinfeld modular varieties I,II" , Cambridge Univ. Press (1996/7) |
| [a13] | G. Laumon, M. Rapoport, U. Stuhler, "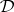 -elliptic sheaves and the Langlands correspondence" Invent. Math. , 113 (1993) pp. 217–338 MR1228127 Zbl 0809.11032 -elliptic sheaves and the Langlands correspondence" Invent. Math. , 113 (1993) pp. 217–338 MR1228127 Zbl 0809.11032 |
| [a14] | H. Niederreiter, C. Xing, "Cyclotomic function fields, Hilbert class fields, and global function fields with many rational places" Acta Arith. , 79 (1997) pp. 59–76 MR1438117 Zbl 0891.11057 |
| [a15] | R. Pink, "The Mumford–Tate conjecture for Drinfeld modules" Publ. RIMS Kyoto Univ. , 33 (1997) pp. 393–425 MR1474696 Zbl 0895.11025 |
| [a16] | H.-G. Rück, U. Tipp, "Heegner points and L-series of automorphic cusp forms of Drinfeld type" Doc. Math., J. DMV , 5 (2000) pp. 365-444 MR1787948 Zbl 1012.11039 |
| [a17] | J. Yu, "Transcendence and Drinfeld modules" Invent. Math. , 83 (1986) pp. 507–517 MR0827364 Zbl 0644.12005 Zbl 0586.12010 |
Drinfel'd module. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Drinfel%27d_module&oldid=24306