Cybernetics

The science of the control, communication and processing of information (literally "helmsmanship" ). The ancient Greek philosopher Plato appears to have been the first to apply this terminology to control in the general sense. A.M. Ampère (1834) suggested the name "Cybernetics" for the science of the management of human society. N. Wiener (1948) used the name "Cybernetics" for the science of control and communication in a living organism and in a machine. The subsequent development of cybernetics has been greatly influenced by the computer. At the beginning of the 1970s, cybernetics finally took shape as a science of mathematical-physical nature with the specific purpose of studying so-called cybernetic systems. Cybernetics systems are an abstraction from a specific (informational) point of view of the complex systems studied by a broad spectrum of natural, technical and social sciences (from their own specific standpoints). By revealing the general aspects in systems of such different nature, cybernetics provides a general and moreover new method of studying them. This is the so-called method of computer simulation, which is intermediate between the classical deductive method and the classical experimental method. Because of this, cybernetics, just like mathematics, can be used as a research technique in other sciences. Furthermore, the spectrum of problems amenable to investigation by cybernetic methods is, by comparison with classical (analytical) mathematical methods, considerably broader and encompasses practically all sciences. In the simplest case, a cybernetic system is reduced to a single element. An element $ A $ of a cybernetic system, considered in an abstract setting, is a quintuple $ \langle x , y , z , f , g \rangle $. The so-called input signal of $ A $ is denoted by $ x = x ( t) $, more precisely, it is a finite set of functions of time $ t $: $ x = \langle x _ {1} ( t) \dots x _ {k} ( t) \rangle $. In many specific cybernetic systems, time is regarded as a parameter taking only a discrete set of values (usually integer values). However, without loss of generality, it is also possible to consider the usual "continuous-time" case (and this is what is done below). For one and the same element $ A $ of a cybernetic system the ranges of values of the functions $ x _ {i} ( t) $ can be different sets of real numbers. Most often, the ranges of the functions are ordinary continuous numerical intervals, the set of integers, or various finite subsets of it. The $ x _ {i} ( t) $ themselves are usually assumed to be piecewise continuous. The symbol $ y $ denotes the output signal $ y = y ( t) $ of the element, being a finite set of functions $ y = \langle y _ {1} ( t) \dots y _ {m} ( t) \rangle $ of the same type as the input functions $ x _ {i} ( t) $. The internal state of the element $ A $ is denoted by $ z = z ( t) $, which is also a finite set of functions $ z = \langle z _ {1} ( t) \dots z _ {n} ( t) \rangle $ of the same type. The symbols $ f $ and $ g $ denote, respectively, functionals giving the current values of the internal state $ z ( t) $ and the output signal $ y ( t) $:

$$ \tag{1 } z ( t) = f ( t , x ( t) , D _ {t} z ( t) ) ; \ \ y ( t) = g ( t , x ( t) , D _ {t} z ( t) ) . $$

Here $ D _ {t} z ( t) $ denotes the restriction of the vector-function $ z ( t) = \langle z _ {1} ( t) \dots z _ {n} ( t) \rangle $ to the domain determined by the half-open intervals $ [ \tau _ {1} , t ) \dots [ \tau _ {n} , t ) $, where the $ \tau _ {i} = \tau _ {i} ( t) $ are piecewise-continuous functions of $ t $ such that $ \tau _ {i} < t $, $ i = 1 \dots n $.

The above definition of an element of a cybernetic system presupposes that the time $ t $ can take arbitrary real values. In practice, these values are restricted to the non-negative numbers in the majority of instances. Moreover, the definition of the element can be supplemented by assigning its initial state $ z _ {0} = z ( 0) $ and also, possibly, its initial output signal $ y _ {0} = y ( 0) $. For this case, the relations (1) are considered only for positive values of $ t $. A complication results from the fact that, besides the deterministic elements of a cybernetic system, one often has to cope with stochastic elements. For this, it usually proves to be sufficient to add, as arguments of the functionals on the right-hand side of (1), a random function $ \omega ( t) $ taking values in a continuous or discrete set of real numbers.

There are further possible generalizations of this definition; in particular the introduction of infinite-dimensional vector-functions for the input signals and for the internal state of the element. It should however be borne in mind that, in contrast to mathematics, a constructive approach to the objects under study is characteristic of cybernetics. This means that there should be a possibility of actually calculating (to some degree of accuracy) the values of all functions under consideration. Therefore, in practice, when studying cybernetic systems, and hence their elements as well, one is sooner or later obliged to turn to finite approximations.

Multi-element cybernetic systems are constructed from a (usually finite) set $ M $ of elements by identifying the output signals of some elements with the input signals of others. Formally such identifications are given by a system of equations

$$ \tag{2 } x _ {i} ^ {p} ( t) = \ y _ {j} ^ {r} ( t) ,\ \ p , r \in M ,\ \ i \in I _ {p} ,\ \ j \in J _ {p} , $$

where $ x _ {i} ^ {p} ( t) $ denotes the $ i $- th component of the input signal of the $ p $- th element and $ y _ {j} ^ {r} ( t) $ the $ j $- th component of the output signal of the $ r $- th element. Under a similar identification (combination of elements of the system), some of the components of the input signals of some of the elements turn out to be free, that is, are not identified with any output components. All such components are combined into the input vector-signal $ x ( t) $ of the system $ S $ under construction. The remaining free components of the output signals form the output signal $ y ( t) $ of the system. In contrast to the input signal, in the output signal $ y ( t) $ there may (according to the definition of the system being constructed) also be an arbitrary number of non-free components of output signals of the elements forming the system $ S $. By definition, the initial state of the system is taken to be the vector consisting of the components of the initial states of all its elements (ordered in some way). The vector $ z ( t) $ defining the state of the system at any moment of time is constructed in a similar manner.

In defining a system in terms of the set of its elements and the set of identifying relations (2), it is necessary to ensure that the definition is well-posed, i.e. that it is possible in fact to calculate the output signal $ y ( t) $ for all $ t > 0 $ given the initial state $ z ( 0) $ of the system and the input signal $ x ( t) $ for all $ t \geq 0 $. A necessary condition for the definition of the system to be well-posed is, for instance, that the range of the function $ y _ {j} ^ {r} ( t) $ in (2) should be contained in the range of values of $ x _ {i} ^ {p} ( t) $. In order to simplify the problem of ensuring the well-posedness of the definition of the system, it is usual not to allow the identification of one input component with more than one output component.

The set of relations (2) defines the structure of the cybernetic system (not to be confused with the abstract notion of a structure in mathematics!). It is useful in a number of applications to consider systems with a variable structure. In this connection, it is possible, by the introduction of additional subsystems, to reduce any system with a variable structure to a system with a constant structure.

The above definition of an abstract cybernetic system encompasses a very large number of specific systems considered in the various areas of knowledge. These include logical networks and networks of abstract automata (cf. Automaton), mechanical dynamical systems, electromechanical and electronic assemblies of various kinds (including computers), biological organisms and their various subsystems (for example the nervous system), and ecological, economic and social systems. In order to be able to consider specific biological, technical and social systems as abstract cybernetic systems, it is necessary to abstract from the majority of their specific properties (such as dimension, mass, chemical structure, the many concrete forms of representing the signals and states, etc.).

The cybernetic aspects of studying systems is a purely informational one. In other words, the states of the elements and their interactions are described by a system of codes with the primary aim of ascertaining a measure of their differences (to within some pre-assigned accuracy of the description), and not of actually measuring certain real physical quantities. For example, if only two voltage levels $ v _ {1} $ and $ v _ {2} $ are involved in an electrical network, they can be defined by numerical codes $ 0 $ and $ 1 $ independently of the actual values of these voltages. It should be pointed out that, although in the definition of a cybernetic system given above only numerical codes are used, it is not difficult to replace them, should the need arise, by alpha-numeric codes using letters of an arbitrary finite alphabet.

Every system with a non-trivial input signal $ x ( t) $ and output signal $ y ( t) $ can be regarded as a processor of information, changing the flow of information $ x ( t) $ into the flow of information $ y ( t) $. In the case of discrete time and finite domains of definition for $ x ( t) $ and $ y ( t) $, the processing (under an appropriate coding of the input information) can be interpreted as a correspondence between words over some fixed pair of alphabets. In this case, the system can be regarded as a discrete information processor. Systems with a non-trivial input signal are called open. In contrast to these, closed systems have no free input components at any of their elements. In such systems the input vector-signal $ x ( t) $ has a zero number of components and consequently cannot carry any information. Closed systems in the strict sense of the word can have neither an input nor an output. However, even in this case they can be regarded as generators of information by considering the change with time of their internal state $ z ( t) $. In what follows, it will be convenient to regard generation as a special case of information processing.

For cybernetic systems, the problems of their analysis and synthesis are highly important. The problem of analysis of a system consists in the determination of the various properties of information processing given by the system; in particular, the presentation in convenient form of an algorithm for the processing. In the latter case, it is really a question of aggregation (composition) of the system into a single element. The problem of synthesis of a system is the opposite of the problem of analysis. It is necessary in the description of the processing to be done by a system to construct a system that actually carries out this processing. As a starting point it is necessary of course to define the class of elements from which the required system has to be constructed.

Of great significance is the problem of finding formal transformations of cybernetic systems which do not alter the processing (and possibly also other invariants) determined by these systems. This then leads to various definitions of equivalence of systems, making it possible to pose the problem of optimization, that is, the problem of finding in a class of equivalent systems a system with extremal values of functionals defined on the systems in the class.

The problem of decomposition involves the representation of part of the system, or all its elements, in the form of systems consisting of smaller elements (subsystems). Of special importance in a large number of applications are systems representable as a combination of two subsystems (elements), usually called the controlling system (controller) and the controlled system (plant). Such a system can be depicted in diagramatic form (see Fig., where $ A $ denotes the controlling system, and $ B $ the object of control; the letter $ x $ denotes the so-called channel of direct communication (the output of the element $ A $ has been identified with the input of the element $ B $), and $ y $ denotes the channel of reverse communication, $ a $ denotes the input signal of the system (the influence of the surrounding medium and of various kinds of noise), and $ b $ denotes the output signal characterizing the performance of the subsystem $ B $( the effectiveness of the control)).

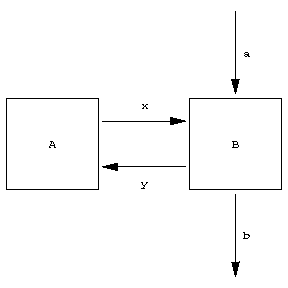
Figure: c027480a

For such systems the problem of synthesis is generally posed in the following way: For a given system $ B $, a given class of external influences $ a $ and a given criterion for the control effectiveness $ b $, to construct a controlling system $ A $ ensuring the specified criterion for the control performance $ b $. Falling within this definition are problems of synthesis of open loop control ( $ b $ being a vector-function of time), servomechanisms (minimizing the vector $ b - a $ in some sense or other), systems of optimal control (systems that direct the controlled plant into some desirable region of its state space in minimal time), etc.

An important place in the theory of cybernetic systems is occupied by the problem of ensuring that systems function in a reliable fashion. Here, the cybernetic aspect of reliability is concerned with questions of the organization of the system itself (redundancy of elements and their communication, special coding systems, etc.), rather than ensuring the physical reliability of the elements and their intercommunications.

For sufficiently simple systems, the majority of the problems listed above (if not in full, then at least in a simplified formulation) can be solved by classical mathematics augmented by some minor variations. For complex systems, which one is obliged to deal with in practice, these methods prove, as a rule, to be unsuitable. Here one means by the complexity of systems not so much quantitative complexity (the number of elements, the number of communications, the dimension of the state, input and output vectors) as primarily the basic qualitative complexity. A system is called complex in this sense if there are no simple descriptions for it. This presupposes, besides a large number of elements in use and a large diversity of their parameters (assumed irreducible), a large diversity and irregularity of the communications between the elements. An effective investigation of such systems by classical deductive methods turns out to be a practical impossibility. The classical experimental method of investigation also proves to be applicable only within very restricted limits. In many cases, such an application is restricted by the high cost of the experiment, and in a number of cases (meteorology, ecology, macro-economics, etc.) natural experiments are either completely impossible or at any rate excessively risky.

One therefore uses as a method of investigating complex cybernetic systems the method of computer simulation by turning to the new powerful universal methods of scientific knowledge which have arisen as a result of the emergence of high-speed general-purpose computers. The method of machine simulation is based in its pure form on the use of so-called simulation models. Such models are in essence a simple translation of the descriptions of the systems being modelled into computer codes. Special programs implementing the model generate the various concrete realizations of the input signal $ x ( t) $ of the system being modelled, and construct, in accordance with the description of the system introduced into the computer (including its initial state), the output signal $ y ( t) $. Thereupon, as for an ordinary experiment (in nature), the results obtained are processed by means of special programs consisting, for example, of histograms of the distributions of various quantities characterizing the behaviour of the system under study, determining the various qualitative characteristics (namely that the system and the information processing defined by it should belong to some class or other), etc. First and foremost, problems of analysis of cybernetic systems are solved by this method. For the solution of the problems of synthesis and optimization by the method of computer simulation, the system of computer programs implementing the experiment is supplemented by setting up an interactive dialogue between the computer and the human investigator, and by introducing modifications into the description of the system being modelled by human intervention, and by implementing also means of providing procedures for automatic processing and organizing the corresponding modifications.

Transferring the description of the cybernetic system to a computer code is a somewhat time-consuming process. Therefore the equipment of computer simulation nowadays includes special compilers (or interpreters) which automatically transform into machine code system model languages specially developed for this purpose. The basis of such model languages consists in a means (suitable for the researcher) of providing the actual description of the parameters, the functions and communications used in the description of the systems. By preserving universality, as a rule (that is, the possibility of describing arbitrary systems), the model languages are usually oriented towards a simpler and easier description of the systems than certain other classes of languages. Furthermore, these model languages include additional means of describing the procedures implementing the computer simulation described above. At present (1987) dozens of universal and specialized languages have been developed for system modelling and for resulting computer simulations; the Western languages include Simula, Simscript, while the Soviet ones include Sleng, Nedis and others.

In many systems of computer simulation, the methods are supplemented by the possibility of using the analytical apparatus of some branches of mathematics (for example, queueing theory), as well as modern computing methods. In the first place, this has to do with various kinds of methods of optimization: linear programming, dynamic programming, gradient methods, stochastic programming, etc.

In the study of cybernetic systems, it turns out advisable in a number of cases to supplement computer simulation with simulation in nature. In this connection, some parts of the cybernetic systems to be modelled are presented to the general-purpose computer (via special translations) in the form of natural models, while the modelling of the remaining parts, the control by the experiment and the processing of its results are carried out in the general-purpose computer using the method described earlier. The use of general-purpose and specialized computers for the automation of control by natural experiments, as well as for the gathering and processing of the experimental data obtained, is an important trend towards the perfection of the research process in all experimental sciences. Even so, pure computer simulation has extensive possibilities for application.

The relation of cybernetics to mathematics is not restricted solely to the use of mathematical methods in cybernetics. Mathematics and cybernetics also have common objects of investigation. Thus, algorithms, for example, which are an object of research in the mathematical theory of algorithms, can at the same time be regarded as cybernetic systems and are both a means and an object of study in cybernetics. However, the mathematical and cybernetic approaches differ greatly. For mathematics, the algorithm stands out primarily as one of the fundamental concepts in the foundations of mathematics. The main problem, therefore, consists in the study of general properties of this concept, for which it is necessary to reduce its definition to a minimum number of simple basic concepts and operations. Cybernetics sets itself the problem of developing suitable methods in practice for the synthesis of concrete systems, among them algorithms. This practical approach necessitates the development of problem- and procedure-oriented algorithmic languages that are suitable for applications (cf. Algorithmic language). Instead of being concerned with the possibility of establishing equivalence of certain classes of algorithms, which is characteristic for mathematics, cybernetics is primarily interested in the creation of apparatus suitable for the actual implementation of equivalent transformations of algorithms. Instead of the simplest form for the representation of information, as words over an abstract alphabet, cybernetics studies the complex data structures that are necessary for the effective realization of algorithms on a computer. The examples mentioned characterize fairly clearly the special nature of the cybernetic approach to the study of its mathematical objects. The same difference in approach can be detected in the cybernetic study of other mathematical objects (abstract automata, logical networks, etc.).

Of special interest from the point of view of the interrelation between cybernetics and mathematics is the approach of each of them to the apparatus of classical mathematical logic. The mathematical point of view presupposes a maximal simplification of the axiom system and deduction rules, without which an effective analysis of its general properties and of the feasibility of logical calculi (cf. Logical calculus) is impossible. Cybernetics, by posing the problem of the automation of deductive constructions by practical means, started to develop the language of practical mathematical logic. The language relates to that of mathematical logic and, as a modern programming language (for example, Algol-68) to the language of Post algorithms or Markov's normal algorithms. The deduction rules in this language (in their interaction with actual meaningful mathematical texts) have a demonstrative power which is no less than that concealed in the word "obvious" in current mathematical monographs.

The automation of deductive constructions is one of the most important parts of this branch of cybernetics, and is termed "artificial intelligenceartificial intelligence" . The natural human intellect (the brain together with organs that receive and deliver external information) is one of the most interesting and complex cybernetic systems. The problem concerning how man thinks has been and continues to be a most interesting and fascinating scientific question. Cybernetics approaches its solution both from the theoretical as well as the practical angle. It is a question of automation (full or partial with human intervention) of the various aspects of human intellectual activity and, in the end, of intelligence as a whole.

Besides the automation of logical thought (deductive constructions), important constituents of the problem of "artificial intelligence" are problems of pattern recognition (primarily visual and aural), operations in natural human languages (recognition of the meaning of sentences and expressions, maintaining a dialogue, etc.), problems of instruction and self-instruction, etc. Of great importance are the problems of the study and synthesis of effective algorithms for the control of the movements of the artificial limbs of humanoid robots, the synthesis of an artificial voice, voice control, etc. A special group of problems arises in the study of purposeful behaviour, the methods of choosing goals, subgoals and schemes for their achievement. A practical approach to the creation of artificial intelligence lies in the creation of dialogue (human—machine) systems, that increase the productivity of the human in various areas of intellectual activity (logical deduction, translation from one natural language to another, chess playing, etc.).

As these become perfected, the role played by the computer in collaborative work will continually increase right up to a full automation of the corresponding process.

Of great importance in two senses is the question of the interrelation between cybernetics and modern computer technology. First, the computer is the basic instrument of investigation for cybernetics, and secondly, it stands out, being the most complex of cybernetic systems, as an important object of investigation in cybernetics. Of course there are many problems which have to be solved when actually designing a computer that do not enter into cybernetics. However, the questions of the architecture of computers and computer systems, the organization of the control by the computing process (including the organization of data bases) fall within the competence of cybernetics and constitute one of its more important branches. This is worth bearing in mind, since it shows up the distinction in the subject matter of cybernetics as understood in the USSR from that as understood in the West (primarily America), where questions of architecture and control of computing systems relate specifically to "computer science" and are not included in cybernetics.

Cybernetic systems are encountered in practically all areas of knowledge. Systems, differing in certain specific properties, can be studied by cybernetic methods specially adapted to the systems of the corresponding classes. In this way a deeper study of them becomes possible. Thus, specialized applied branches of cybernetics have arisen and continue to be developed, such as technological cybernetics, economic cybernetics, biological cybernetics, medical cybernetics, and military cybernetics. The application of mathematical and cybernetic methods in linguistics has given rise to the topic called mathematical linguistics. This science is directly related to linguistic problems of artificial intelligence.

References

[1]	N. Wiener, "Cybernetics" , Wiley & M.I.T. (1948)
[2]	W.R. Ashby, "Introduction to cybernetics" , Chapman & Hall (1956)
[3]	V.M. Gluskov, "Introduction to cybernetics" , Kiev (1964) (In Russian)
[4]	, Encyclopaedia of cybernetics , 1–2 , Kiev (1974) (In Russian)

Comments

As already stated in the main article above, in Western literature the term "cybernetics" is used in a way different from that in the USSR. Below the Western view is presented. It is convenient to start with a definition.

Cybernetics is a field of scientific inquiry which is concerned with the study of man-made systems. As such, it distinguishes itself from the descriptive nature of the physical sciences and from the purely logical structure and aims of mathematics. Cybernetics comprises (parts of) such fields as control theory (cf. Control system), communication theory (cf. Communication channel), information processing, operations research, computer science (cf. Computer, abstract), decision theory, mathematical statistics, etc.

The term "cybernetics" has achieved much more popularity in the USSR and Eastern Europe than it has in North America and Western Europe. The difficulty with the term is that it is not clear what it comprises and, consequently, that it is not clear what it does not comprise.

It is not easy to discover a unifying theme in the field of cybernetics. As already mentioned, the field is mainly concerned with man-made systems and, as such, as primary importance to engineering and management science. All this implies that cybernetic fields have a strong prescriptive aspect; it tends to concentrates on design: synthesis, not analysis, is the main feature. Unfortunately, in actual fact, cybernetics is composed of a number of specialities with little overlap and a small common basis. Among the unifying ideas is the use of the mathematical language, of optimization techniques for formulating and achieving goals, and of stochastic models for uncertainty. An important but not dominating role is furthermore played by dynamics, that is, the study of the evolution in time of systems.

The definition of a cybernetic system presented in the main article is an attempt to give a definition of a dynamical system in input-state-output form. From a mathematical point of view it is possible to approach this goal in a more logical and direct way. Thus, it is possible to define a dynamical system $ \Sigma $ to be a triple $ \Sigma = ( T , W , B ) $ with $ T \subseteq \mathbf R $ the time set, $ W $ the signal alphabet ( $ W $ need not be a finite or countable set), and $ B \subseteq W ^ {T} $ the behaviour: $ B $ tells which time trajectories are and which are not compatible with the laws governing $ \Sigma $. In most applications $ T $ is either $ \mathbf Z $ or $ \mathbf R $ and $ \Sigma $ is time-invariant, that is, it is assumed that $ \sigma ^ {t} B = B $ for all $ t \in T $, where $ \sigma ^ {t} $ denotes the $ t $- shift: $ ( \sigma ^ {t} f ) ( t ^ \prime ) = f ( t + t ^ \prime ) $. In the sequel it is assumed that $ T = \mathbf Z $ or $ \mathbf R $ and that $ \Sigma $ is time-invariant.

It is possible to refine this definition so that the state of the system also becomes part of the structure. A state space system $ \Sigma _ {s} $ is defined to be a quadruple $ \Sigma _ {s} = ( T , W , X , B _ {s} ) $ with $ T $, $ W $ as above, $ X $ the state space, and $ B _ {s} \subseteq ( W \times X ) ^ {T} $ the internal behaviour. The behaviour $ B : = \{ {W } : {\exists x \textrm{ such that } ( w , x ) \in B _ {s} } \} $ is called the external behaviour. One should think of $ w $ as the observable variables or, better, the variables which are being modelled, and of $ x $ as a latent auxiliary variable which describes the memory of the system. This structure is formalized by assuming that $ B _ {s} $ satisfies the axiom of state, requiring the implication

$$ \{ ( w _ {1} , x _ {1} ) \in B _ {s} , ( w _ {2} , x _ {2} ) \in B _ {s} ,\ x _ {1} ( 0) = x _ {2} ( 0) \} \rightarrow $$

$$ \rightarrow \ \{ ( w _ {1} , x _ {1} ) \wedge ( w _ {2} , x _ {2} ) \} . $$

Here $ \wedge $ denotes concatenation:

$$ ( f _ {1} \wedge f _ {2} ) ( t) : = \ \left \{ \begin{array}{ll} f _ {1} ( t) & \textrm{ for } t < 0 , \\ f _ {2} ( t) & \textrm{ for } t \geq 0 . \\ \end{array} \right .$$

Examples of discrete-time systems are formal languages; examples of discrete-time state space systems are automata. In many applications $ B $ is specified by an evolution law in terms of a differential or difference equation. If this differential or difference equation is of order one in $ x $ and of order zero in $ w $, one obtains a state space system.

State space models have important advantages in problems of control, communication, information processing, etc., as exemplified by the popularity of dynamic programming. The topic concerned with associating a state space model with given external behaviour is called realization theory. Elegant realization algorithms are available on a set-theoretic level and also for special classes of systems, particularly for linear systems.

In many dynamical systems it is possible to split the external variables into inputs, causes, and outputs, effects. Combining this cause-effect structure with the memory structure of state models and assuming that the dynamics are described by an evolution law, yields the following class of models

$$ \sigma x = f ( x , u ) ,\ y = h ( x , u ) \ \ ( \textrm{ discrete time } ) , $$

$$ \dot{x} = f ( x , u ) ,\ y = h ( x , u ) \ ( \textrm{ continuous time } ) . $$

These models, combined with initial and terminal conditions, are particularly useful in dynamic decision making (control theory, cf. also Automatic control theory) and computer science (automata theory, cf. Automata, theory of). In this latter area time is usually logic time, i.e. it expresses sequencing, and necessarily clock time.

The above class of dynamical systems has emerged and been studied very much in cybernetic fields. The presence of the input (control) variables makes this class of models very suitable for design-type questions. The presence of the output (measured) variables makes it very suitable for information-processing questions. However, in reality the above definitions are nothing more than general models for dynamics, and also physical systems (as Maxwell's equations, Newton's laws, etc.) show this structure. As such, calling these cybernetic systems is an inappropriate use of terminology.

In interconnecting systems, one usually assigns outputs of some subsystems to function as inputs to other subsystems. An important interconnection is the feedback loop shown in Fig.a1.

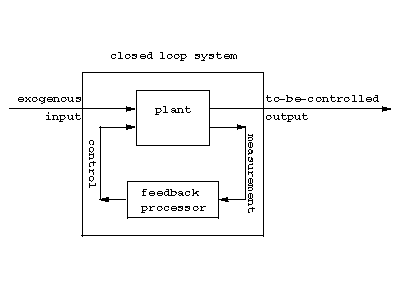
Figure: c027480b

By designing the feedback processor suitably, it is possible to achieve certain desired properties (stability, optimality, etc.) of the closed loop system.

The distinguishing feature of cybernetics is, in Western opinion, that in this way one achieves purposeful systems. The various subsystems are not independent but are designed or have evolved such that one subsystem will function and adapt its functioning relative to another subsystem.

Some of the interesting cybernetic structures which have been developed in mathematical system and control theory are observers or filters, identification systems, and adaptive control mechanisms. They yield internal model principles, the separation principle, certainty equivalent control, etc. The structure of the interconnected systems obtained this way can be viewed as a concern of cybernetics. In the long run the ideas underlying these principles may become part of the core of cybernetics.

Even though computation plays an important role in cybernetics, it does not seem realistic or productive to classify simulation methods or such parts of computer science as computer languages and architecture as cybernetics. The field of artificial science on the other hand can, as far as its goals and problems are concerned, indeed be considered to be part of cybernetics.

References

[a1]	J.C. Willems, "Models for dynamics" , Dynamics reported , Wiley & Teubner (Forthcoming)
[a2]	H.A. Simon, "The science of the artificial" , M.I.T. (1969)