Automatic control theory

The science dealing with methods for the determination of laws for controlling systems that can be realized by automatic devices. Historically, such methods were first applied to processes which were mainly technical in nature [1]. Thus, an aircraft in flight is a system the control laws of which ensure that it remains on the required trajectory. The laws are realized by means of a system of transducers (measuring devices) and actuators, which is known as the automatic pilot. This development was due to three reasons: many control systems had been identified by classical science (to identify a control system means to write down its mathematical model, e.g. relationships such as (1) and (2) below); long before the development of automatic control theory, thanks to the knowledge of the fundamental laws of nature, there was a well-developed mathematical apparatus of differential equations and especially an apparatus for the theory of steady motion [2]; engineers had discovered the idea of a feedback law (see below) and found means for its realization.

The simplest control systems are described by an ordinary (vector) differential equation

$$ \tag{1 } \dot{x} = f ( x, u , t ) $$

and an inequality

$$ \tag{2 } N ( x, u , t ) \geq 0, $$

where $ x \{ x _ {1} \dots x _ {n} \} $ is the state vector of the system, $ u \{ u _ {1} \dots u _ {r} \} $ is the vector of controls which can be suitably chosen, and $ t $ is time. Equation (1) is the mathematical representation of the laws governing the control system, while the inequality (2) establishes its domain of definition.

Let $ U $ be some given class of functions $ u(t) $( e.g. piecewise-continuous functions) whose numerical values satisfy (2). Any function $ u(t) \in U $ will be called a permissible control. Equation (1) will be called a mathematical model of the control system if:

1) A domain $ N (x, u , t) \geq 0 $ in which the function $ f(x, u , t) $ is defined has been specified;

2) A time interval $ {\mathcal T} = [ t _ {i} , t _ {f} ] $( or $ [t _ {i} , t _ {f} ) $, if $ t _ {f} = \infty $) during which the motion $ x(t) $ is observed, has been specified;

3) A class of permissible controls has been specified;

4) The domain $ N \geq 0 $ and the function $ f(x, u , t) $ are such that equation (1) has a unique solution defined for any $ t \in {\mathcal T} $, $ x _ {0} \in N $, whatever the permissible control $ u(t) $. Furthermore, $ f(x, u , t) $ in (1) is always assumed to be smooth with respect to all arguments.

Let $ x _ {i} = x(t _ {i} ) $ be an initial and let $ x _ {f} = x(t _ {f} ) $ be a (desired) final state of the control system. The state $ x _ {f} $ is known as the target of the control. Automatic control theory must solve two major problems: the problem of programming, i.e. of finding those controls $ u(t) $ permitting the target to be reached from $ x _ {i} $; and the determination of the feedback laws (see below). Both problems are solved under the assumption of complete controllability (1).

The system (1) is called completely controllable if, for any $ x _ {i} , x _ {f} \in N $, there is at least one permissible control $ u(t) $ and one interval $ {\mathcal T} $ for which the control target is attainable. If this condition is not met, one says that the object is incompletely controllable. This gives rise to a preliminary problem: Given the mathematical model (1), find the criteria of controllability. At the time of writing (1977) only insignificant progress has been made towards its solution. If equation (1) is linear

$$ \tag{3 } \dot{x} = Ax + Bu, $$

where $ A, B $ are stationary matrices, the criterion of complete controllability is formulated as follows: For (3) to be completely controllable it is necessary and sufficient that the rank of the matrix

$$ \tag{4 } Q = \| B AB \dots A ^ {n-1 } B \| $$

be $ n $. The matrix (4) is known as the controllability matrix.

If $ A, B $ are known differentiable functions of $ t $, the controllability matrix is given by

$$ \tag{5 } Q = \| L _ {1} ( t ) \dots L _ {n} ( t ) \| , $$

where

$$ L _ {1} ( t ) = B ( t ),\ L _ {k} ( t ) = A ( t ) L _ {k-1 } - dL _ \frac{k-1 }{dt} ,\ k = 2 \dots n. $$

The following theorem applies to this case: For (3) to be completely controllable it is sufficient if at at least one point $ t ^ {*} \in {\mathcal T} $ the rank of the matrix (5) equals $ n $[3]. Criteria of controllability for non-linear systems are unknown (up to 1977).

The first principal task of automatic control theory is to select the permissible controls that ensure that the target $ x _ {f} $ is attained. There are two methods of solving this problem. In the first method, the chief designer of the system (1) arbitrarily determines a certain type of motion for which the target $ x _ {f} $ is attainable and selects a suitable control. This solution of the programming problem is in fact used in many instances. In the second method a permissible control minimizing a given cost of controls is sought. The mathematical formulation of the problem is then as follows. The data are: the mathematical model of the controlled system (1) and (2); the boundary conditions for the vector $ x $, which will be symbolically written as

$$ \tag{6 } ( i, f ) = 0; $$

a smooth function $ G(x, t) $; and the cost of the controls used

$$ \tag{7 } \Delta G = \left . G ( x, t ) \right | _ {i} ^ {f} . $$

The programming problem is to find, among the permissible controls, a control satisfying conditions (6) and yielding the minimum value of the functional (7). Necessary conditions for a minimum for this non-classical variational problem are given by the L.S. Pontryagin "maximum principle" [4] (cf. Pontryagin maximum principle). An auxiliary vector $ \psi \{ \psi _ {1} \dots \psi _ {n} \} $ and the auxiliary scalar function

$$ \tag{8 } H ( \psi , x, u , t ) = \psi \cdot f ( x, u , t ) $$

are introduced. The function $ H $ makes it possible to write equation (1) and an equation for the vector $ \psi $ in the following form:

$$ \tag{9 } \dot{x} = \frac{\partial H }{\partial \psi } ,\ \dot \psi = - \frac{\partial H }{\partial x } . $$

Equation (9) is linear and homogeneous with respect to $ \psi $ and has a unique continuous solution, which is defined for any initial condition $ \psi (t _ {i} ) $ and $ t \in {\mathcal T} $. The vector $ \psi $ will be called a non-zero vector if at least one of its components does not vanish for $ t \in {\mathcal T} $. The following theorem is true: For the curve $ x ^ {o} , u ^ {o} $ to constitute a strong minimum of the functional (7) it is necessary that a non-zero continuous vector $ \psi $, as defined by equation (9), exists at which the function $ H( \psi , x, u , t) $ has a (pointwise) maximum with respect to $ u $, and that the transversality condition

$$ \left [ \delta G - H \delta t + \sum \psi _ \alpha \delta x _ {a} \right ] _ {i} ^ {f} = 0 $$

is met. Let $ x ^ {o} ( t, x _ {i} , x _ {f} ) , u _ {o} ( t, x _ {i} , x _ {f} ) $ be solutions of the corresponding problem. It has then been shown that for stationary systems the function $ H( \psi ^ {o} , x ^ {o} , u ^ {o} ) $ satisfies the condition

$$ \tag{10 } H ( \psi ^ {o} , x ^ {o} , u ^ {o} ) = C , $$

where $ C $ is a constant, so that (10) is a first integral. The solution $ u ^ {o} , x ^ {o} $ is known as a program control.

Let $ u ^ {o} , x ^ {o} $ be a (not necessarily optimal) program control. It was found that the knowledge of only one program control is insufficient to attain the target. This is because the program $ u ^ {o} , x ^ {o} $ is usually unstable with respect to, however small, changes in the problem, in particular to the most important changes, those in the initial and final values $ (i, f) $ or, in other words, the problem is ill-posed. However, this ill-posedness is such that it can be corrected by means of automatic stabilization, based solely on the "feedback principle" . Hence the second main task of control: the determination of feedback laws.

Let $ y $ be the vector of disturbed motion of the system and let $ \xi $ be the vector describing the additional deflection of the control device intended to quench the disturbed motion. To realize the deflection $ \xi $ a suitable control source must be provided for in advance. The disturbed motion is described by the equation:

$$ \tag{11 } \dot{y} = Ay + B \xi + \phi ( y , \xi , t ) + f ^ {o} ( t ) . $$

where $ A $ and $ B $ are known matrices determined by the motion of $ x ^ {o} , u ^ {o} $, and are assumed to be known functions of the time; $ \phi $ is the non-linear part of the development of the function $ f(x, u , t) $; $ f ^ {o} (t) $ is the constantly acting force of perturbation, which originates either from an inaccurate determination of the programmed motion or from additional forces which were neglected in constructing the model (1). Equation (11) is defined in a neighbourhood $ \| y \| \leq \overline{H}\; $, where $ \overline{H}\; $ is usually quite small, but in certain cases may be any finite positive number or even $ \infty $.

It should be noted that, in general, the fact that the system (1) is completely controllable does not mean that the system (11) is completely controllable as well.

One says that (11) is observable along the coordinates $ y _ {1} \dots y _ {r} $, $ r \leq n $, if one has at his disposal a set of measuring instruments that continuously determines the coordinates at any moment of time $ t \in {\mathcal T} $. The significance of this definition can be illustrated by considering the longitudinal motion of an aircraft. Even though aviation is more than 50 years old, an instrument that would measure the disturbance of the attack angle of the aircraft wing or the altitude of its flight near the ground has not yet been invented. The totality of measured coordinates is called the field of regulation and is denoted by $ P ( y _ {1} \dots y _ {r} ) $, $ r \leq n $.

Consider the totality of permissible controls $ \xi $, determined over the field $ P $:

$$ \tag{12 } \xi = \xi ( y _ {1} \dots y _ {r} , t , p ),\ r \leq n, $$

where $ p $ is a vector or a matrix parameter. One says that the control (12) represents a feedback law if the closure operation (i.e. substitution of (12) into (11)) yields the system

$$ \tag{13 } \dot{y} = Ay + B \xi ( y _ {1} \dots y _ {r} , t , p ) + $$

$$ + \phi ( y , \xi ( y _ {1} \dots y _ {r} , t , p ), t ), $$

such that its undisturbed motion $ y = 0 $ is asymptotically stable (cf. Asymptotically-stable solution). The system (13) is said to be asymptotically stable if its undisturbed motion $ y = 0 $ is asymptotically stable.

There are two classes of problems which may be formulated in the context of the closed system (13): The class of analytic and of synthetic problems.

Consider a permissible control (12) given up to the selection of the parameter $ p $, e.g.:

$$ \xi = \left \| \begin{array}{ccc} p _ {11} &\dots &p _ {1r} \\ \dots &\dots &\dots \\ p _ {r1} &\dots &p _ {rr} \\ \end{array} \right \| \ \left \| \begin{array}{c} {y _ {1} } \\ . \\ . \\ {y _ {r} } \\ \end{array} \ \right \| . $$

The analytic problem: To determine the domain $ S $ of values of the parameter $ p $ for which the closed system (13) is asymptotically stable. This domain is constructed by methods developed in the theory of stability of motion (cf. Stability theory), which is extensively employed in the theory of automatic control. In particular, one may mention the methods of frequency analysis; methods based on the first approximation to Lyapunov stability theory (the theorems of Hurwitz, Routh, etc.), on the direct Lyapunov method of constructing $ v $- functions, on the Lyapunov–Poincaré theory of constructing periodic solutions, on the method of harmonic balance, on the B.V. Bulgakov method, on the A.A. Andronov method, and on the theory of point transformations of surfaces [5]. The last group of methods makes it possible not only to construct domains $ S $ in the space $ P $, but also to analyze the parameters of the stable periodic solutions of equation (13) which describe the auto-oscillatory motion of the system (13). All these methods are widely employed in the practice of automatic control, and are studied in the framework of various specifications in schools of higher learning [5].

If $ S $ is non-empty, a control (12) is called a feedback law or regulation law. Its realization, which is effected using a system of measuring instruments, amplifiers, converters and executing mechanisms, is known as a regulator.

Another problem of considerable practical importance, which is closely connected with the analytic problem, is how to construct the boundary of the domain of attraction [6], [7]. Consider the system (13) in which $ p \in S $. The set of values $ y(t _ {i} ) = y _ {0} $ containing the point $ y = 0 $ for which the closed system (13) retains the property of asymptotic stability, is known as the domain of attraction of the trivial solution $ y = 0 $. The problem is to determine the boundary of the domain of attraction for a given closed system (13) and a point $ p \in S $.

Modern scientific literature does not contain effective methods of constructing the boundary of the domain of attraction, except in rare cases in which it is possible to construct unstable periodic solutions of the closed system. However, there are certain methods which allow one to construct the boundary of a set of values of $ y _ {0} $ totally contained in the domain of attraction. These methods are based in most cases on the evaluation of a domain in phase space in which the Lyapunov function satisfies the condition $ v \geq 0 $, $ \dot{v} \leq 0 $[7].

Any solution $ y(t, y _ {0} , p) $ of the closed system (13) represents a so-called transition process. In most cases of practical importance the mere solution of the stability problem is not enough. The development of a project involves supplementary conditions of considerable practical importance, which require the transition process to have certain additional features. The nature of these requirements and the list of these features are closely connected with the physical nature of the controlled object. In analytic problems it may often be possible, by a suitable choice of the parameter $ p $, to preserve the desired properties of the transition process, e.g. the pre-set regulation time $ t ^ {*} $. The problem of choosing the parameter $ p $ is known as the problem of quality of regulation [5], and methods for solving this problem are connected with some construction of estimates for solutions $ y(t, y _ {0} , p) $: either by actual integration of equation (13) or by experimental evaluation of such solutions with the aid of an analogue or digital computer.

The analytic problems of transition processes have many other formulations in all cases in which $ f ^ {o} (t) $ is a random function — in servomechanisms for example, [5], [8]. Other formulations are concerned with the possibility of a random alteration of the matrices $ A $ and $ B $ or even of the function $ \phi $[5], [8]. This gave rise to the development of methods for studying random processes, methods of adaptation and learning machines [9]. Transition processes in systems with delay mechanisms and with distributed parameters (see [10], [11]) and with a variable structure (see [12]) have also been studied.

The synthesis problem: Given equation (11), a field of regulation $ P (y _ {1} \dots y _ {r} ) $, $ r \leq n, $ and a set $ \xi (y _ {1} \dots y _ {r} , t) $ of permissible controls, to find the whole set $ M $ of feedback laws [13]. One of the most important variant of this problem is the problem of the structure of minimal fields. A field $ P ( y _ {1} \dots r _ {r} ) $, $ r \leq n, $ is called a minimal field if it contains at least one feedback law and if the dimension $ r $ of the field is minimal. The problem is to determine the structure $ P ( y _ {\alpha _ {1} } \dots y _ {\alpha _ {r} } ) $ of all minimal fields for a given equation (11) and a set of permissible controls. The following example illustrates the nature of the problem:

$$ \dot{z} = Az + Bu, $$

$$ A = \left \| \begin{array}{rrrr} 0 & m & 0 & 0 \\ -m & 0 & 0 & n \\ 0 & 0 & 0 & k \\ 0 &-n & k & 0 \\ \end{array} \right \| ,\ B = \left \| \begin{array}{rr} 0 & 0 \\ 1 & 0 \\ 0 & 0 \\ 0 & 1 \\ \end{array} \right \| ,\ u = \left \| \begin{array}{r} u _ {2} \\ u _ {4} \\ \end{array} \right \| , $$

where $ m, n, k $ are given numbers. The permissible controls are the set of piecewise-continuous functions $ u _ {2} , u _ {4} $ that take their values from the domain

$$ | u _ {2} | \leq \overline{u}\; _ {2} ,\ | u _ {4} | \leq \overline{u}\; _ {4} . $$

The minimal fields in this problem are either the field $ P ( z _ {2} ) $ or the field $ P ( z _ {4} ) $. The dimension of each field is one and cannot be reduced [13].

So far (1977) only one method is known for the synthesis of feedback laws; it is based on Lyapunov functions [13]. A relevant theorem is that of Barbashin–Krasovskii [6], [10], [15]: In order for the undisturbed motion $ y= 0 $ of the closed system

$$ \tag{14 } \dot{y} = \phi ( y ) $$

to be asymptotically stable, it is sufficient for a positive-definite function $ v(y) $ to exist, such that by equation (14) its complete derivative is a function $ w(y) $ which is semi-definite negative, and such that on the manifold $ w(y) = 0 $ no complete trajectory of the system (14), except for $ y = 0 $, lies. The problem of finding out about the existence and the structure of the minimal fields is of major practical importance, since these fields determine the possible requirements of the chief designer concerning the minimum weight, complexity and cost price of the control system and its maximum reliability. The problem is also of scientific and practical interest in connection with infinite-dimensional systems as encountered in technology, biology, medicine, economics and sociology.

In designing control systems it is unfortunately impracticable to restrict the work to solving problems of synthesis of feedback laws. In most cases the requirements of the chief designer are aimed at securing certain important specific properties of the transition process in the closed system. The importance of such requirements is demonstrated by the importance of monitoring an atomic reactor. If the transition process takes more than 5 seconds or if the maximum value of some of its coordinates exceeds a certain value, an atomic explosion follows. This gives rise to new problems of synthesis of regulation laws, based on the set $ M $. Below the formulation of one such problem is given. Consider two spheres $ \| y _ {0} \| = R $, $ y _ {0} = y _ {i} $, $ \| y (t _ {1} ) \| = \epsilon $; $ R \gg \epsilon $ are given numerical values. Now consider the set $ M $ of all feedback laws. The closure by means of any of them yields the equation:

$$ \tag{15 } \dot{y} = Ay + B \xi ( y _ {1} \dots y _ {r} , t ) + $$

$$ \phi ( y , \xi ( y _ {1} \dots y _ {r} , t ) , t ) . $$

Consider the entire set of solutions $ y (t, y _ {0} ) $ of equation (15) which start on the sphere $ R $ and call them $ R $- solutions. Since the system is asymptotically stable for any $ y _ {0} $ on the sphere, there exists a moment of time $ t _ {1} $ during which the conditions

$$ \| y ( t _ {1} , y _ {0} ) \| = \epsilon ,\ \ \| y ( t , y _ {0} ) \| < \epsilon , $$

are valid for any $ t > t _ {1} $.

Let

$$ t ^ {*} = \sup _ {y _ {0} } t _ {1} . $$

It is clear from the definition of $ t _ {1} $ that $ t ^ {*} $ exists. The interval $ t ^ {*} - t _ {i} $ is called the regulation time (the time of damping of the transition process) in the closed system (15) if any arbitrary $ R $- solution starts at the $ \epsilon $- sphere if $ t _ {1} \leq t ^ {*} $, but remains inside it if $ t > t _ {1} $. It is clear that the regulation time is a functional of the form $ t ^ {*} = t ^ {*} (R, \epsilon , \xi ) $. Let $ T $ be a given number. There arises the problem of synthesis of fast-acting regulators: Given a set $ M $ of feedback laws, one has to isolate its subset $ M _ {1} $ on which the regulation time in a closed system satisfies the condition

$$ t ^ {*} - t _ {i} \leq T . $$

One can formulate in a similar manner the problems of synthesis of the sets $ M _ {2} \dots M _ {k} $ of feedback laws, which satisfy the other $ k - 1 $ requirements of the chief designer.

The principal synthesis problem of satisfying all the requirements of the chief designer is solvable if the sets $ M _ {1} \dots M _ {k} $ have a non-empty intersection [13].

The synthesis problem has been solved in greatest detail for the case in which the field $ P $ has maximal dimension, $ r = n $, while the cost index of the system is characterized by the functional

$$ \tag{16 } J = \int\limits _ { 0 } ^ \infty w ( y , \xi , t ) dt , $$

where $ w (y, \xi , t) $ is a positive-definite function of $ y, \xi $. The problem is then known as the problem of analytic construction of optimum regulators [14] and is in fact thus formulated. The data include equation (11), a class of permissible controls $ \xi (y, t) $ defined over the field $ P(y) $ of maximal dimension, and the functional (16). One is required to find a control $ \xi = \xi (y, t) $ for which the functional (16) assumes its minimum value. This problem is solved by the following theorem: If equation (11) is such that it is possible to find an upper semi-continuous positive-definite function $ v ^ {o} (y, t) $ and a function $ \xi ^ {o} (y, t) $ such that the equality

$$ \tag{17 } \frac{\partial v ^ {o} }{\partial t } + \frac{\partial v ^ {o} }{\partial y } ( Ay + B \xi ^ {o} + \phi ( y , \xi ^ {o} , t ) ) = 0 $$

is true, and the inequality

$$ \frac{\partial v ^ {o} }{\partial t } + \frac{\partial v ^ {o} }{\partial y } ( Ay + B \xi + \phi ( y , \xi , t )) \geq 0 $$

is also true for all permissible $ \xi $, then the function $ \xi ^ {o} (y, t) $ is a solution to the problem. Morever, the equality

$$ v ^ {o} ( t _ {0} , y _ {0} ) = \mathop{\rm min} _ \xi \int\limits _ { 0 } ^ \infty w ( y , \xi , t ) dt $$

is true. The function $ v ^ {o} (y, t) $ is known as the Lyapunov optimum function [15]. It is a solution of the partial differential equation (17), of Hamilton–Jacobi type, satisfying the condition $ v(y ( \infty ), \infty ) = 0 $. Methods for the effective solution of such a problem have been developed for the case in which the functions $ w $ and $ \phi $ can be expanded in a convergent power series in $ y , \xi $ with coefficients which are bounded continuous functions of $ t $. Of fundamental importance is the solvability of the problem of linear approximation to equation (11) and the optimization with respect to the integral of only second-order terms contained in the development of $ w $. This problem is solvable if the condition of complete controllability is satisfied [15].

References

[1]	D.K. Maksvell, I.A. Vishnegradskii, A. Stodola, "The theory of automatic regulation" , Moscow (1942) (In Russian)
[2]	N.G. Chetaev, "Stability of motion" , Moscow (1965) (In Russian) MR1139513 MR0561646 Zbl 0760.34045 Zbl 0095.29003 Zbl 0061.42004
[3]	N.N. Krasovskii, "Theory of control of motion" , Moscow (1968) (In Russian) MR0265035 Zbl 1082.93576
[4]	L.S. Pontryagin, V.G. Boltayanskii, R.V. Gamkrelidze, E.F. Mishchenko, "The mathematical theory of optimal processes" , Wiley (1962) (Translated from Russian) MR0166036 MR0166037 MR0166038 Zbl 0102.32001
[5]	, Technical cybernetics , Moscow (1967) Zbl 0189.27801
[6]	E.A. Barbashin, "Introduction to the theory of stability" , Wolters-Noordhoff (1970) (Translated from Russian) MR0264141 Zbl 0198.19703
[7]	V.I. Zubov, "Mathematical methods of studing systems of automatic control" , Leningrad (1959) (In Russian)
[8]	V.S. Pugachev, "Theory of random functions and its application to control problems" , Pergamon (1965) (Translated from Russian) MR0177829
[9]	Ya.Z. Tsypkin, "Foundations of the theory of learning systems" , Acad. Press (1973) (Translated from Russian) MR0434545 Zbl 0258.93019
[10]	N.N. Krasovskii, "Stability of motion. Applications of Lyapunov's second method to differential systems and equations with delay" , Stanford Univ. Press (1963) (Translated from Russian) MR0147744
[11]	V.A. Besekerskii, E.P. Popov, "The theory of automatic control systems" , Moscow (1966) (In Russian)
[12]	S.V. Emelyanov (ed.) , Theory of systems with a variable structure , Moscow (1970) (In Russian)
[13]	A.M. Letov, "Some unsolved problems in control theory" Differential equations N.Y. , 6 : 4 (1970) pp. 455–472 Differentsial'nye Uravneniya , 6 : 4 (1970) pp. 592–615 Zbl 0249.93036
[14]	A.M. Letov, "Dynamics of flight and control" , Moscow (1969) (In Russian)
[15]	I.G. Malkin, "Theorie der Stabilität einer Bewegung" , R. Oldenbourg , München (1959) (Translated from Russian) MR0104029 Zbl 0124.30003

Comments

The article above reflects a different tradition and terminology than customary in the non-Russian literature. It also almost totally ignores the vast amount of important results concerning automatic (optimal) control theory that have appeared in the non-Russian literature.

Roughly speaking a control system is a device whose future development (either in a deterministic or stochastic sense) is determined entirely by its present state and the present and future values of the control parameters. The "recipe" which determines future behaviour can be almost anything, e.g. a differential equation

$$ \tag{a1 } \dot{x} = f ( x , u , t ) ,\ \ x \in \mathbf R ^ {n} ,\ \ u \in \mathbf R ^ {m} ,\ \ t \in \mathbf R , $$

as in the main article above, or a difference equation

$$ \tag{a2 } x _ {t+1} = f ( x _ {t} , u _ {t} , t ) ,\ \ x _ {t} \in \mathbf R ^ {n} ,\ \ u _ {t} \in \mathbf R ^ {m} ,\ \ t = 0 , 1 \dots $$

or more generally, a differential equation with delays, an evolution equation in some function space, a more general partial differential equation $ \dots $ or any combination of these. Frequently there are constraints on the values the control $ u \in \mathbf R ^ {m} $ may take, e.g., $ \| u \| \leq M $ where $ M $ is a constant. However there certainly are (engineering) situations when the controls $ u (t) $ which can be used at time $ t $ depend both explicitly on time and the current state $ x (t) $ of the system (which of course in turn depends on the past controls used). This may make it complicated to describe the space of admissible or permissible controls in simple terms.

It may even be not very well possible to describe the control structure in such terms as equations (a1) and constraints $ N ( x , u , t ) \geq 0 $ defined on $ \mathbf R ^ {n} \times \mathbf R ^ {m} \times \mathbf R $. This happens, e.g., in the case of the control of an artificial satellite where the space $ \mathbf R ^ {m} $ in which the controls take their value may depend on the state $ x $, being, e.g., the tangent space to a sphere at the point $ x $. Then controls become sections in a vector bundle usually subject to further size constraints.

At this point some of the natural and traditional problems concern reachability, and controllability and state space feedback. Give an initial state $ x (0) $ the control system is said to be completely reachable (from $ x (0) $) if for all states $ x $ there is an admissible control steering $ x (0) $ to $ x $. This is termed complete controllability in the article above. Controllability in the Western literature is usually reserved for the opposite notion: Given a (desired) final state $ x (f) $ the system is said to be completely controllable (to $ x (f) $) if for every possible initial state $ x $ there is a control which steers $ x $ to $ x (f) $. In the case of continuous-time, time-invariant, finite-dimensional systems the two notions coincide, but this is not always the case.

There are also many result on reachability and controllability for non-linear systems, especially for local controllability and reachability. These results often are stated in terms of Lie algebras associated to the control system. E.g., for a control system of the form

$$ \tag{a3 } \dot{x} = f (x) + \sum _ { i=1 } ^ { m } u _ {i} g _ {i} (x) ,\ \ x \in \mathbf R ^ {n} ,\ \ u \in \mathbf R ^ {m} , $$

one considers the Lie algebra $ {\mathcal L} ( \Sigma ) $ spanned by the vector fields $ ( \mathop{\rm ad} f ) ^ {k} ( g _ {i} ) $, $ i = 1 \dots m $; $ k = 0 , 1 \dots $ where $ \mathop{\rm ad} f (g) = [ f , g ] $, $ ( \mathop{\rm ad} f ) ^ {k} = ( \mathop{\rm ad} f ) \circ ( \mathop{\rm ad} f ) ^ {k-1} $. Given a Lie algebra of vector fields $ {\mathcal L} $ on a manifold $ M $ the rank of $ {\mathcal L} $ at a point $ x \in M $, $ \mathop{\rm rk} _ {x} {\mathcal L} $, is the dimension of the space of tangent vectors $ \{ {X (x) } : {X \in {\mathcal L} } \} \subset T _ {x} M $. A local reachability result now says that $ \mathop{\rm rk} _ {x} {\mathcal L} ( \Sigma ) = n $ implies local reachability at $ x $. There are also various global and necessary-condition-type results especially in the case of analytic systems. Cf. [a2], [a10], [a14] for a first impression of the available results.

Given a control system (a1) an important general question concerns to what extent it can be changed by feedback, in this case state space feedback. This means the following. A state space feedback law is a suitable mapping $ k : \mathbf R ^ {n} \rightarrow \mathbf R ^ {m} $, $ x \mapsto u = k (x) $. Inserting this in (a1) results in the closed loop system $ \dot{x} = f ( x , k (x) , t ) $. Cf. Fig. a.

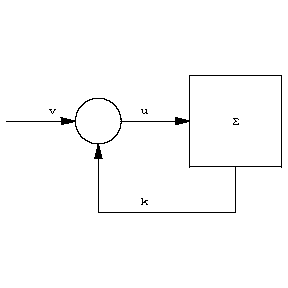
Figure: a014090a

Often "new" controls $ v \in \mathbf R ^ {m} $ are also introduced and one considers, e.g. the new control system $ \dot{x} = f (x , k (x) + v , t ) $ or, more generally, $ \dot{x} = f ( x , k ( x , v ) , t ) $. Dynamic feedback laws in which the function $ k ( x , v ) $ is replaced by a complete input-output system (cf. below)

$$ \tag{a4 } \dot{y} = g ( y , x , v , t ) ,\ \ u = h (y) , $$

are also frequently considered. Important questions now are, e.g., whether for a given system (a1) a $ k (x) $ or $ k ( x , v ) $ or system (a4) of various kinds can be found such that the resulting closed loop system is stable. Or, whether by means of feedback a system can be linearized or imbedded in a linear system (4). Cf. [a6] for a selection of results.

Using (large) controls in engineering situations can be expensive. This leads to the idea of a control system with cost functional $ J $ which is often given in terms such as

$$ J (u) = \int\limits _ { t _ {0} } ^ { {t _ 1 } } g ( x , u , t ) d t + F ( x ( t _ {1} ) ) . $$

There result optimal control questions such as finding that admissible function $ u $ which minimizes $ J (u) $( and steers $ x $ to the target set) (optimal open loop control) and finding a minimizing feedback control law $ u = k (x) $( optimal closed loop control). In practice the case of a linear system (4) with a quadratic criterion is very important, the so called $ L Q $ problem. Then

$$ \tag{a5 } G ( x , u , t ) = \ u ^ {T} R u + 2 u ^ {T} S x + x ^ {T} Q x ,\ \ F (x) = x ^ {T} M x . $$

Here the upper $ {} ^ {T} $ denotes transpose and $ R , S , Q , M $ are suitable matrices (which may depend on time as may $ A $ and $ B $). In this case under suitable positive-definiteness assumptions on $ R , M $ and the block matrix

$$ \left \| \begin{array}{cc} R & S \\ S ^ {T} & Q \\ \end{array} \right \| , $$

the optimal solution exists. It is of feedback type and is obtained as follows. Consider the matrix Riccati equation

$$ \tag{a6 } \dot{K} = - A K - K A + ( S + B ^ {T} K ) ^ {T} R ^ {-1} ( S + B ^ {T} K ) - Q , $$

$$ K ( t _ {1} ) = M . $$

Solve it backwards up to time $ t _ {0} $. Then the optimal control is given by

$$ \tag{a7 } u = - R ^ {-1} ( B ^ {T} K + S ) x $$

The solution (method) extends to the case where the linear system is in addition subject to Gaussian stochastic disturbances, cf. [a9], [a17].

Also for non-linear systems there are synthesis results for optimal (feedback) control. One can, for instance, use the Pontryagin maximum principle to determine the optimal (open loop) control for each initial state $ x \in \mathbf R ^ {n} $( if it exists and is unique). This yields a mapping $ x \mapsto u $ which is a candidate for an optimal feedback control law and under suitable regularity assumptions this is indeed the case, cf. [a3], [a15]. Some standard treatises on optimal control in various settings are [a5], [a12], [a13].

In many situations it cannot be assumed that the state $ x $ of a control system (a1) is directly accessible for control purposes, e.g. for the implementation of a feedback law. More generally only certain derived quantities are immediately observable. (Think for example of the various measuring devices in an aircraft as compared to the complete state description of the aircraft.) This leads to the idea of an input-output (dynamical) system, or briefly (dynamical) system, also called plant (cf. Fig. b),

$$ \tag{a8 } \dot{x} = f ( x , u , t ) ,\ \ y = h ( x , u , t ) , $$

$$ x \in \mathbf R ^ {n} ,\ u \in \mathbf R ^ {m} ,\ y \in \mathbf R ^ {p} . $$

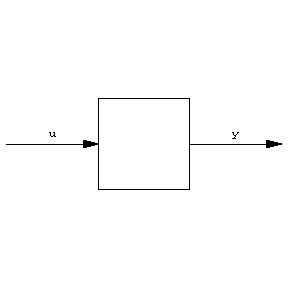
Figure: a014090b

Here the $ u \in \mathbf R ^ {m} $ are viewed as controls or inputs and the $ y \in \mathbf R ^ {p} $ as observations or outputs. Let $ x ( t , u ; x _ {0} ) $ denote the solution of the first equation of (a8) for the initial condition $ x ( t _ {0} ) = x _ {0} $ and a given $ u (t) $. The system (a8) is called completely observable if for any two initial states $ x _ {0} , x _ {0} ^ \prime \in \mathbf R ^ {n} $ and (known) control $ u $ there holds that $ y ( x ( t , u ; x _ {0} ) , u , t ) = y ( x ( t , u ; x _ {0} ^ \prime ) , u , t ) $ for all $ t \geq t _ {0} $ implies $ x _ {0} = x _ {0} ^ \prime $. This is more or less what is meant by the phrase "observability along coordinates93B07observable along the coordinates y1…yn" in the main article above. In the case of a time-invariant linear system

$$ \tag{a9 } \dot{x} = A x + B u ,\ \ y = C x , $$

complete observability holds only if and only the (block) observability matrix $ \| C ^ {T} C ^ {T} A ^ {T} \dots C ^ {T} ( A ^ {T} ) ^ {n-1} \| $ is of full rank $ n $. This is completely dual to the reachability (controlability) result for linear systems in the article above.

In this setting of input-output systems many of the problems indicated above acquire an output analogue, e.g. output feedback stabilization, where (in the simplest case) a function $ u = k (y) $ is sought such that $ \dot{x} = f ( x , k ( h ( x , u , t ) , t )) $ is (asymptotically) stable, the dynamic output feedback problem and the optimal output feedback control problem. In addition new natural questions arise such as whether it is possible by means of some kind of feedback to make certain outputs independent of certain inputs (decoupling problems). In case that there are additional stochastic disturbances possibly both in the evolution of $ x $ and in the measurements $ y $ problems of filtering are added to all this. E.g. the problem of finding the best estimate $ \widetilde{x} (t) $ of the state of the system given the observations $ y (s) $, $ t _ {0} \leq s \leq t $, [a9].

There is also the so-called realization problem. Given an initial state $ x _ {0} $ a system such as (a8) defines a mapping from a space of input functions $ u $ to a space of output functions $ y $, and the question arises which mappings can be realized by means of systems such as (a8). Cf. [a6] for a survey of results in this direction in the non-linear deterministic case and [a9] for results in the linear stochastic case.

With the notable exception of the output feedback problem one can say at the present time that the theory of linear time-invariant finite-dimensional systems, possibly with Gaussian noise and quadratic cost criteria, is in a highly-satisfactory state. Cf., e.g., the standard treatise [a11]. Generalization of this substantial body of results to a more general setting seems to require sophisticated mathematics, e.g. algebraic geometry and algebraic $ K $- theory in the case of families of linear systems [a8], [a16], functional analysis and contraction semi-groups for infinite-dimensional linear systems [a4], functional analysis, interpolation theory and Fourier analysis for filtering and prediction [a9], and foliations, vector bundles, Lie algebras of vector fields and other notions from differential topology and geometry for non-linear systems theory [a2], [a9].

A great deal of research at the moment is concerned with systems with unknown (or uncertain) parameters. Here adaptive control is important. This means that one attempts to design e.g. output feedback control laws which automatically adjust themselves to the unknown parameters.

A good idea of the current state of the art of system and control theory can be obtained by studying the proceedings of the yearly IEEE CDC (Institute of Electronic and Electrical Engineers Conference on Decision and Control) conferences and the biyearly MTNS (Mathematical Theory of Networks and Systems) conferences.

References

[a1]	S. Barnett, "Introduction to mathematical control theory" , Oxford Univ. Press (1975) MR0441413 Zbl 0307.93001
[a2]	R.W. Brockett, "Nonlinear systems and differential geometry" Proc. IEEE , 64 (1976) pp. 61–72 MR0432255
[a3]	P. Brunovsky, "On the structure of optimal feedback systems" , Proc. Internat. Congress Mathematicians (Helsinki, 1978) , 2 , Acad. Sci. Fennicae (1980) pp. 841–846 MR0562697 Zbl 0425.49019
[a4]	R.F. Curtain, A.J. Pritchard, "Infinite-dimensional linear system theory" , Springer (1978) MR0516812
[a5]	W.H. Fleming, R.W. Rishel, "Deterministic and stochastic optimal control" , Springer (1975) MR0454768 Zbl 0323.49001
[a6]	M. Fliess (ed.) M. Hazewinkel (ed.) , Algebraic and geometric methods in nonlinear control theory , Reidel (1986) MR0862315 Zbl 0596.00024
[a7]	M. Hazewinkel, "On mathematical control engineering" Gazette des Math. , 28, July (1985) pp. 133–151
[a8]	M. Hazewinkel, "(Fine) moduli spaces for linear systems: what are they and what are they good for" C.I. Byrnes (ed.) C.F. Martin (ed.) , Geometric methods for linear system theory , Reidel (1980) pp. 125–193 MR0608993 Zbl 0481.93023
[a9]	M. Hazewinkel (ed.) J.C. Willems (ed.) , Stochastic systems: the mathematics of filtering and identification , Reidel (1981) MR0674319 Zbl 0486.00016
[a10]	V. Jurdjevic, I. Kupka, "Control systems on semi-simple Lie groups and their homogeneous spaces" Ann. Inst. Fourier , 31 (1981) pp. 151–179 MR644347 Zbl 0453.93011
[a11]	H. Kwakernaak, R. Sivan, "Linear optimal control systems" , Wiley (1972) MR0406607 Zbl 0276.93001
[a12]	L. Markus, "Foundations of optimal control theory" , Wiley (1967) MR0220537 Zbl 0159.13201
[a13]	J.-L. Lions, "Optimal control of systems governed by partial differential equations" , Springer (1971) (Translated from French) MR0271512 Zbl 0203.09001
[a14]	C. Lobry, "Controlabilité des systèmes non-linéaires" , Outils et modèles mathematiques pour l'automatique, l'analyse des systémes et le traitement du signal , 1 , CNRS (1981) pp. 187–214
[a15]	H.J. Sussmann, "Analytic stratifications and control theory" , Proc. Internat. Congress Mathematicians (Helsinki, 1978) , 2 , Acad. Sci. Fennicae (1980) pp. 865–871 MR0562701 Zbl 0499.93023
[a16]	A. Tannenbaum, "Invariance and system theory: algebraic and geometric aspects" , Springer (1981) MR0611155 Zbl 0456.93001
[a17]	J.C. Willems, "Recursive filtering" Statistica Neerlandica , 32 (1978) pp. 1–39 MR0465454 Zbl 0379.93003
[a18]	G. Wunsch (ed.) , Handbuch der Systemtheorie , Akademie Verlag (1986) MR0900145 MR0852214 Zbl 0642.93001

🛠️ This page contains images that should be replaced by better images in the SVG file format. 🛠️