Isotopy (in algebra)

This page is deficient and requires revision. Please see Talk:Isotopy (in algebra) for further comments.

A relation on the class of all groupoids (cf. Groupoid) defined on a given set 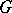. Namely, two groupoids on 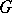are called isotopic if there exist permutations 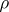, 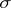and of 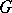such that for any ,

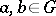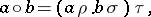where and denote the operations in these two groupoids. The isotopy relation is an equivalence relation for the binary operations on 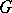. An isomorphism of two binary operations defined on the same set is a special case of an isotopy (with 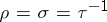). An isotopy is called principal if is the identity permutation. Every isotope (i.e. isotopic groupoid) of a groupoid is isomorphic to a principal isotope of the groupoid. Every groupoid that is isotopic to a quasi-group is itself a quasi-group. Every quasi-group is isotopic to some loop (Albert's theorem). If a loop (in particular, a group) is isotopic to some group, then they are isomorphic. If a groupoid with identity is isotopic to a semi-group, then they are isomorphic, that is, they are both semi-groups with identity.

References

[1]	A.G. Kurosh, "Lectures on general algebra" , Chelsea (1963) (Translated from Russian)

References

[a1]	R.H. Bruck, "A survey of binary systems" , Springer (1971)