Difference between revisions of "Whitehead homomorphism"
Ulf Rehmann (talk | contribs) m (tex encoded by computer) |
(latex details) |
||
| Line 17: | Line 17: | ||
to the stable homotopy group of the spectrum of the sphere $ S ^ {0} $, | to the stable homotopy group of the spectrum of the sphere $ S ^ {0} $, | ||
defined in a special way. One construction of the Whitehead group is by the Hopf construction: A mapping $ \phi : S ^ {m} \rightarrow \mathop{\rm SO} ( q) $ | defined in a special way. One construction of the Whitehead group is by the Hopf construction: A mapping $ \phi : S ^ {m} \rightarrow \mathop{\rm SO} ( q) $ | ||
| − | determines a mapping $ ( J \phi ) : S ^ {m} \times S ^ {q-} | + | determines a mapping $ ( J \phi ) : S ^ {m} \times S ^ {q-1} \rightarrow S ^ {q-1} $, |
which can be extended to a mapping $ J \phi : S ^ {m} \times E ^ {q} \rightarrow E _ {+} ^ {q} $ | which can be extended to a mapping $ J \phi : S ^ {m} \times E ^ {q} \rightarrow E _ {+} ^ {q} $ | ||
of $ S ^ {m} \times E ^ {q} $ | of $ S ^ {m} \times E ^ {q} $ | ||
to the upper hemi-sphere of $ S ^ {q} $. | to the upper hemi-sphere of $ S ^ {q} $. | ||
| − | There is also an extension $ J \phi : E ^ {m+} | + | There is also an extension $ J \phi : E ^ {m+1} \times S ^ {q-1} \rightarrow E _ {-} ^ {q} $ |
to the lower hemi-sphere of $ S ^ {q} $, | to the lower hemi-sphere of $ S ^ {q} $, | ||
| − | and this determines a mapping $ J \phi : S ^ {m+} | + | and this determines a mapping $ J \phi : S ^ {m+q} \rightarrow S ^ {q} $. |
This construction gives a mapping of homotopy classes, and so defines a homomorphism $ J: \pi _ {m} ^ {S} ( \mathop{\rm SO} ) \rightarrow \pi _ {m} ^ {S} ( S ^ {0} ) $, | This construction gives a mapping of homotopy classes, and so defines a homomorphism $ J: \pi _ {m} ^ {S} ( \mathop{\rm SO} ) \rightarrow \pi _ {m} ^ {S} ( S ^ {0} ) $, | ||
called the Whitehead group. | called the Whitehead group. | ||
| Line 104: | Line 104: | ||
An elementary check shows that $ f \times \mathop{\rm id} $ | An elementary check shows that $ f \times \mathop{\rm id} $ | ||
is compatible with the corresponding equivalence relations, and hence defines a mapping $ \Gamma f $ | is compatible with the corresponding equivalence relations, and hence defines a mapping $ \Gamma f $ | ||
| − | as desired. Recall that $ S ^ {m} \star S ^ {n} \cong S ^ {m+ | + | as desired. Recall that $ S ^ {m} \star S ^ {n} \cong S ^ {m+n+1} $, |
| − | cf. [[ | + | cf. [[Join]]. |
Now, let $ \phi : S ^ {m} \rightarrow \mathop{\rm SO} ( q) $ | Now, let $ \phi : S ^ {m} \rightarrow \mathop{\rm SO} ( q) $ | ||
be a mapping; each element of $ \mathop{\rm SO} ( q) $ | be a mapping; each element of $ \mathop{\rm SO} ( q) $ | ||
| − | induces a mapping $ S ^ {q-} | + | induces a mapping $ S ^ {q-1} \rightarrow S ^ {q-1} $ |
of the $ ( q- 1) $- | of the $ ( q- 1) $- | ||
sphere into itself. Hence $ \phi $ | sphere into itself. Hence $ \phi $ | ||
| Line 115: | Line 115: | ||
$$ | $$ | ||
| − | \widetilde \phi : S ^ {m} \times S ^ {q-} | + | \widetilde \phi : S ^ {m} \times S ^ {q-1} \rightarrow S ^ {q-1} . |
$$ | $$ | ||
| Line 122: | Line 122: | ||
$$ | $$ | ||
| − | S ^ {m+} | + | S ^ {m+q} \cong S ^ {m} \star S ^ {q-1} \mathop \rightarrow \limits ^ { {\Gamma \widetilde \phi }} \ |
| − | S( S ^ {q-} | + | S( S ^ {q-1} ) \cong S ^ {q} . |
$$ | $$ | ||
====References==== | ====References==== | ||
<table><TR><TD valign="top">[a1]</TD> <TD valign="top"> B. Gray, "Homotopy theory. An introduction to algebraic topology" , Acad. Press (1975) pp. 334 {{MR|0402714}} {{ZBL|0322.55001}} </TD></TR><TR><TD valign="top">[a2]</TD> <TD valign="top"> R.M. Switzer, "Algebraic topology - homotopy and homology" , Springer (1975) pp. 480ff {{MR|0385836}} {{ZBL|0305.55001}} </TD></TR></table> | <table><TR><TD valign="top">[a1]</TD> <TD valign="top"> B. Gray, "Homotopy theory. An introduction to algebraic topology" , Acad. Press (1975) pp. 334 {{MR|0402714}} {{ZBL|0322.55001}} </TD></TR><TR><TD valign="top">[a2]</TD> <TD valign="top"> R.M. Switzer, "Algebraic topology - homotopy and homology" , Springer (1975) pp. 480ff {{MR|0385836}} {{ZBL|0305.55001}} </TD></TR></table> | ||
Revision as of 20:31, 16 January 2024
$ J $-
homomorphism
A homomorphism from the stable homotopy group of the spectrum of $ \mathop{\rm SO} $ to the stable homotopy group of the spectrum of the sphere $ S ^ {0} $, defined in a special way. One construction of the Whitehead group is by the Hopf construction: A mapping $ \phi : S ^ {m} \rightarrow \mathop{\rm SO} ( q) $ determines a mapping $ ( J \phi ) : S ^ {m} \times S ^ {q-1} \rightarrow S ^ {q-1} $, which can be extended to a mapping $ J \phi : S ^ {m} \times E ^ {q} \rightarrow E _ {+} ^ {q} $ of $ S ^ {m} \times E ^ {q} $ to the upper hemi-sphere of $ S ^ {q} $. There is also an extension $ J \phi : E ^ {m+1} \times S ^ {q-1} \rightarrow E _ {-} ^ {q} $ to the lower hemi-sphere of $ S ^ {q} $, and this determines a mapping $ J \phi : S ^ {m+q} \rightarrow S ^ {q} $. This construction gives a mapping of homotopy classes, and so defines a homomorphism $ J: \pi _ {m} ^ {S} ( \mathop{\rm SO} ) \rightarrow \pi _ {m} ^ {S} ( S ^ {0} ) $, called the Whitehead group.
This homomorphism was first constructed by G.W. Whitehead , who also proved a theorem on the non-triviality of the infinite series of homotopy groups of spheres, $ \pi _ {n} ( S ^ {r} ) \neq 0 $, for the following values of $ n $ and $ r $:
<tbody> </tbody>
|
The stable homotopy groups $ \pi _ {m} ^ {S} ( \mathop{\rm SO} ) $ are described by the Bott periodicity theorem [2]:
<tbody> </tbody>
|
The image of the Whitehead homomorphism has been completely calculated (cf. [4], [5]): for $ m \equiv 0 $( $ \mathop{\rm mod} 8 $) and $ m> 0 $ the Whitehead group is a monomorphism and its image is a direct summand in the group $ \pi _ {m} ^ {S} ( S ^ {0} ) $; for $ m\equiv 1 $( $ \mathop{\rm mod} 8 $) and $ m> 1 $ the Whitehead group is a monomorphism on a direct summand of $ \pi _ {m} ^ {S} ( S ^ {0} ) $; for $ m= 4s- 1 $ the image of the Whitehead group is the cyclic group of order $ \tau ( 2s) $, giving a direct summand in $ \pi _ {m} ^ {S} ( S ^ {0} ) $, where $ \tau ( 2s) $ is the denominator of the irreducible fraction $ B _ {s} /( 4s) $, $ B _ {s} $ being the $ s $- th Bernoulli number (cf. Bernoulli numbers).
References
| [1a] | G.W. Whitehead, "On the homotopy groups of spheres and rotation groups" Ann. of Math. , 43 (1942) pp. 634–640 MR0007107 Zbl 0060.41105 |
| [1b] | G.W. Whitehead, "A generalization of the Hopf invariant" Ann. of Math. , 51 (1950) pp. 192–237 MR0041435 Zbl 0045.44202 Zbl 0041.51903 |
| [2] | R. Bott, "The stable homotopy of the classical groups" Ann. of Math. , 70 (1959) pp. 313–337 MR0110104 Zbl 0129.15601 |
| [3a] | J.F. Adams, "On the groups 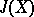 - I" Topology , 2 (1963) pp. 181–195 - I" Topology , 2 (1963) pp. 181–195 |
| [3b] | J.F. Adams, "On the groups 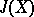 - II" Topology , 3 (1965) pp. 137–171 - II" Topology , 3 (1965) pp. 137–171 |
| [3c] | J.F. Adams, "On the groups 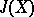 - III" Topology , 3 (1965) pp. 193–222 - III" Topology , 3 (1965) pp. 193–222 |
| [3d] | J.F. Adams, "On the groups 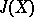 - IV" Topology , 5 (1966) pp. 21–71 - IV" Topology , 5 (1966) pp. 21–71 |
| [4] | J.C. Becker, D.H. Gottlieb, "The transfer map and fiber bundles" Topology , 14 (1975) pp. 1–12 MR0377873 Zbl 0306.55017 |
| [5] | J.F. Adams, "Infinite loop spaces" , Princeton Univ. Press (1978) MR0505692 Zbl 0398.55008 |
Comments
Given a mapping $ f: X \times Y \rightarrow Z $ of topological spaces, quite generally the Hopf construction gives a mapping
$$ \Gamma f : X \star Y \rightarrow SZ $$
from the join $ X \star Y $ of $ X $ and $ Y $ to the suspension $ SZ $ of $ Z $, as follows. Consider
$$ f \times \mathop{\rm id} : X \times Y \times I \rightarrow Z \times I,\ \ ( x, y, t) \mapsto ( f( x, y), t). $$
The join $ X \star Y $ is a certain quotient space of $ X \times Y \times Z $ and $ SZ $ is a quotient space of $ Z \times I $. An elementary check shows that $ f \times \mathop{\rm id} $ is compatible with the corresponding equivalence relations, and hence defines a mapping $ \Gamma f $ as desired. Recall that $ S ^ {m} \star S ^ {n} \cong S ^ {m+n+1} $, cf. Join.
Now, let $ \phi : S ^ {m} \rightarrow \mathop{\rm SO} ( q) $ be a mapping; each element of $ \mathop{\rm SO} ( q) $ induces a mapping $ S ^ {q-1} \rightarrow S ^ {q-1} $ of the $ ( q- 1) $- sphere into itself. Hence $ \phi $ induces a mapping
$$ \widetilde \phi : S ^ {m} \times S ^ {q-1} \rightarrow S ^ {q-1} . $$
Applying the Hopf construction to $ \widetilde \phi $ gives the mapping $ J \phi $:
$$ S ^ {m+q} \cong S ^ {m} \star S ^ {q-1} \mathop \rightarrow \limits ^ { {\Gamma \widetilde \phi }} \ S( S ^ {q-1} ) \cong S ^ {q} . $$
References
| [a1] | B. Gray, "Homotopy theory. An introduction to algebraic topology" , Acad. Press (1975) pp. 334 MR0402714 Zbl 0322.55001 |
| [a2] | R.M. Switzer, "Algebraic topology - homotopy and homology" , Springer (1975) pp. 480ff MR0385836 Zbl 0305.55001 |
Whitehead homomorphism. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Whitehead_homomorphism&oldid=55151