Difference between revisions of "Si-ci-spiral"
From Encyclopedia of Mathematics
(TeX) |
|||
| Line 13: | Line 13: | ||
====References==== | ====References==== | ||
| − | <table><TR><TD valign="top">[1]</TD> <TD valign="top"> E. Jahnke, F. Emde, F. Lösch, "Tafeln höheren Funktionen" , Teubner (1966)</TD></TR></table> | + | <table><TR><TD valign="top">[1]</TD> <TD valign="top"> E. Jahnke, F. Emde, F. Lösch, "Tafeln höheren Funktionen" , Teubner (1966)</TD></TR> |
| + | <TR><TD valign="top">[a1]</TD> <TD valign="top"> M. Abramowitz, I.A. Stegun, "Handbook of mathematical functions" , Dover, reprint (1972)</TD></TR></table> | ||
| − | + | {{OldImage}} | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
Latest revision as of 19:17, 11 January 2024
A plane curve whose equation in rectangular Cartesian coordinates $(x,y)$ has the form
$$x=\operatorname{ci}(t),\quad y=\operatorname{si}(t),$$
where $\operatorname{ci}$ is the integral cosine, $\operatorname{si}$ is the integral sine and $t$ is a real parameter (see Fig.).
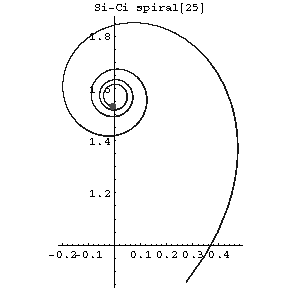
Figure: s084980a
The arc length from $t=0$ to $t=t_0$ is equal to $\log t_0$, and the curvature is equal to $\kappa=t_0$.
References
| [1] | E. Jahnke, F. Emde, F. Lösch, "Tafeln höheren Funktionen" , Teubner (1966) |
| [a1] | M. Abramowitz, I.A. Stegun, "Handbook of mathematical functions" , Dover, reprint (1972) |
🛠️ This page contains images that should be replaced by better images in the SVG file format. 🛠️
How to Cite This Entry:
Si-ci-spiral. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Si-ci-spiral&oldid=54981
Si-ci-spiral. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Si-ci-spiral&oldid=54981
This article was adapted from an original article by D.D. Sokolov (originator), which appeared in Encyclopedia of Mathematics - ISBN 1402006098. See original article