Si-ci-spiral
From Encyclopedia of Mathematics
A plane curve whose equation in rectangular Cartesian coordinates $(x,y)$ has the form
$$x=\operatorname{ci}(t),\quad y=\operatorname{si}(t),$$
where $\operatorname{ci}$ is the integral cosine, $\operatorname{si}$ is the integral sine and $t$ is a real parameter (see Fig.).
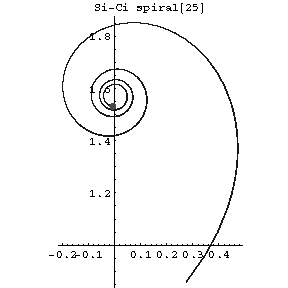
Figure: s084980a
The arc length from $t=0$ to $t=t_0$ is equal to $\log t_0$, and the curvature is equal to $\kappa=t_0$.
References
| [1] | E. Jahnke, F. Emde, F. Lösch, "Tafeln höheren Funktionen" , Teubner (1966) |
| [a1] | M. Abramowitz, I.A. Stegun, "Handbook of mathematical functions" , Dover, reprint (1972) |
🛠️ This page contains images that should be replaced by better images in the SVG file format. 🛠️
How to Cite This Entry:
Si-ci-spiral. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Si-ci-spiral&oldid=54981
Si-ci-spiral. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Si-ci-spiral&oldid=54981
This article was adapted from an original article by D.D. Sokolov (originator), which appeared in Encyclopedia of Mathematics - ISBN 1402006098. See original article