Difference between revisions of "Young tableau"
(image) |
(latex details) |
||
| Line 25: | Line 25: | ||
In Western literature the phrase Ferrers diagram is also used for a Young diagram. In the Russian literature the phrase "Young tableau" ( "Yunga tablitsa" ) and "Young diagram" ( "Yunga diagramma" ) are used precisely in the opposite way, with "tablitsa" referring to the pictorial representation of a partition and "diagramma" being a filled-in "tablitsa" . | In Western literature the phrase Ferrers diagram is also used for a Young diagram. In the Russian literature the phrase "Young tableau" ( "Yunga tablitsa" ) and "Young diagram" ( "Yunga diagramma" ) are used precisely in the opposite way, with "tablitsa" referring to the pictorial representation of a partition and "diagramma" being a filled-in "tablitsa" . | ||
| − | Let $\kappa$ denote a [[partition]] of $m$ ( | + | Let $\kappa$ denote a [[partition]] of $m$ ($\kappa=(\kappa_1,\ldots,\kappa_t)$, $\kappa_i \in \{0,1,\ldots\}$, $\kappa_1+\cdots+\kappa_t=m$) as well as its corresponding [[Young diagram]], its pictorial representation. Let $\lambda$ be a second partition of $m$. A $\kappa$-tableau of type $\lambda$ is a Young diagram $\kappa$ with its boxes filled with <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/y/y099/y099100/y09910025.png" /> <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/y/y099/y099100/y09910026.png" />'s, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/y/y099/y099100/y09910027.png" /> <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/y/y099/y099100/y09910028.png" />'s, etc. For a semi-standard $\kappa$-tableau of type $\lambda$, the labelling of the boxes is such that the rows are non-decreasing (from left to right) and the columns are strictly increasing (from top to bottom). E.g. |
<pre style="font-family: monospace;color:black"> | <pre style="font-family: monospace;color:black"> | ||
| Line 51: | Line 51: | ||
where <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/y/y099/y099100/y09910076.png" /> is the column-stabilizer of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/y/y099/y099100/y09910077.png" />, i.e. the subgroup of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/y/y099/y099100/y09910078.png" /> of all permutations that leave the labels of the columns of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/y/y099/y099100/y09910079.png" /> set-wise invariant. | where <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/y/y099/y099100/y09910076.png" /> is the column-stabilizer of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/y/y099/y099100/y09910077.png" />, i.e. the subgroup of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/y/y099/y099100/y09910078.png" /> of all permutations that leave the labels of the columns of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/y/y099/y099100/y09910079.png" /> set-wise invariant. | ||
| − | The Specht module, | + | The Specht module, $[\mu]$, of $\mu$ is the submodule of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/y/y099/y099100/y09910082.png" /> spanned by all the elements <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/y/y099/y099100/y09910083.png" />, where <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/y/y099/y099100/y09910084.png" /> is the tabloid of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/y/y099/y099100/y09910085.png" /> and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/y/y099/y099100/y09910086.png" /> is a <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/y/y099/y099100/y09910087.png" />-tableau. Over a field of characteristic zero the Specht modules give precisely all the different absolutely-irreducible representations of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/y/y099/y099100/y09910088.png" />. By Young's rule, the number of times that the Specht module <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/y/y099/y099100/y09910089.png" /> over $\mathbf{Q}$ occurs (as a composition factor) in $\rho(\kappa)$ is equal to the Kostka number $K(\kappa,\lambda)$. If $e_t$ is the [[Young symmetrizer]] of a $\mu$-tableau $t$, then the Specht module defined by the underlying diagram is isomorphic to the ideal $F[S_n]e_t$ of $F[S_n]. This is also (up to isomorphism) the representation denoted by $T_{\mu}$ in [[Representation of the symmetric groups]]. Cf. [[Majorization ordering]] for a number of other results involving partitions, Young diagrams and tableaux, and representations of the symmetric groups. |
====References==== | ====References==== | ||
| − | <table><TR><TD valign="top">[a1]</TD> <TD valign="top"> D. Knuth, "The art of computer programming" , '''3''' , Addison-Wesley (1973)</TD></TR></table> | + | <table> |
| + | <TR><TD valign="top">[a1]</TD> <TD valign="top"> D. Knuth, "The art of computer programming" , '''3''' , Addison-Wesley (1973)</TD></TR> | ||
| + | </table> | ||
{{TEX|want}} | {{TEX|want}} | ||
Revision as of 20:32, 14 December 2023
of order $m$
A Young diagram of order $m$ in whose cells the different numbers $1,\ldots,m$ have been inserted in some order, e.g.
┌───┬───┬───┬───┐ │ 5 │ 7 │ 9 │ 4 │ ├───┼───┼───┼───┘ │ 8 │ 2 │ 1 │ ├───┼───┴───┘ │ 3 │ ├───┤ │ 6 │ └───┘
A Young tableau is called standard if in each row and in each column the numbers occur in increasing order. The number of all Young tableaux for a given Young diagram $t$ of order $m$ is equal to $m!$ and the number of standard Young tableaux is $$ \frac{m!}{\prod\lambda_{ij}} $$
where the product extends over all the cells $c_{ij}$ of $t$ and $\lambda_{ij}$ denotes the length of the corresponding hook.
Comments
In Western literature the phrase Ferrers diagram is also used for a Young diagram. In the Russian literature the phrase "Young tableau" ( "Yunga tablitsa" ) and "Young diagram" ( "Yunga diagramma" ) are used precisely in the opposite way, with "tablitsa" referring to the pictorial representation of a partition and "diagramma" being a filled-in "tablitsa" .
Let $\kappa$ denote a partition of $m$ ($\kappa=(\kappa_1,\ldots,\kappa_t)$, $\kappa_i \in \{0,1,\ldots\}$, $\kappa_1+\cdots+\kappa_t=m$) as well as its corresponding Young diagram, its pictorial representation. Let $\lambda$ be a second partition of $m$. A $\kappa$-tableau of type $\lambda$ is a Young diagram $\kappa$ with its boxes filled with 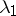
 's,
's, 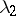
 's, etc. For a semi-standard $\kappa$-tableau of type $\lambda$, the labelling of the boxes is such that the rows are non-decreasing (from left to right) and the columns are strictly increasing (from top to bottom). E.g.
's, etc. For a semi-standard $\kappa$-tableau of type $\lambda$, the labelling of the boxes is such that the rows are non-decreasing (from left to right) and the columns are strictly increasing (from top to bottom). E.g.
┌───┬───┬───┬───┬───┐ │ 1 │ 1 │ 1 │ 1 │ 4 │ ├───┼───┼───┼───┴───┘ │ 2 │ 2 │ 3 │ ├───┼───┼───┘ │ 3 │ 4 │ └───┴───┘
is a semi-standard $(5,3,2)$-tableau of type $(4,2,2,2)$. The numbers $K(\kappa,\lambda)$ of semi-standard $\kappa$-tableaux of type $\lambda$ are called Kostka numbers.
To each partition $\mu$ of $n$, there are associated two "natural" representations of $S_n$, the symmetric group on $n$ letters: the induced representation 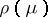 and the Specht module
and the Specht module 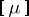 . The representation
. The representation 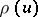 is:
is:
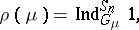 |
where 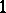 is the trivial representation of
is the trivial representation of 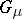 and
and 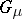 is the Young subgroup of
is the Young subgroup of 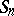 determined by
determined by 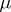 ,
, 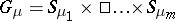 , where
, where 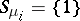 if
if 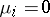 and otherwise
and otherwise 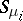 is the subgroup of permutations on the letters
is the subgroup of permutations on the letters 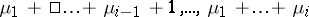 .
.
The group 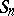 acts on the set of all
acts on the set of all 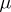 -tableaux by permuting the labels. Two
-tableaux by permuting the labels. Two 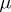 -tableaux are equivalent if they differ by a permutation of their labels keeping the sets of indices in each row set-wise invariant. An equivalence class of
-tableaux are equivalent if they differ by a permutation of their labels keeping the sets of indices in each row set-wise invariant. An equivalence class of 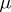 -tableaux is a
-tableaux is a 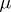 -tabloid. The action of
-tabloid. The action of 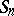 on
on 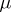 -tableaux induces an action on
-tableaux induces an action on  -tabloids, and extending this linearly over a base field
-tabloids, and extending this linearly over a base field 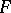 gives a representation of
gives a representation of 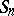 which is evidently isomorphic to
which is evidently isomorphic to 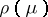 . The dimension of
. The dimension of 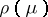 is
is 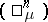 . Given a
. Given a 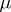 -tableau
-tableau 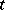 , let
, let 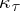 be the following element of
be the following element of 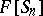 :
:
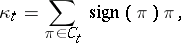 |
where 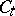 is the column-stabilizer of
is the column-stabilizer of 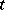 , i.e. the subgroup of
, i.e. the subgroup of 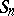 of all permutations that leave the labels of the columns of
of all permutations that leave the labels of the columns of 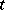 set-wise invariant.
set-wise invariant.
The Specht module, $[\mu]$, of $\mu$ is the submodule of 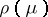 spanned by all the elements
spanned by all the elements 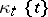 , where
, where 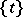 is the tabloid of
is the tabloid of 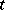 and
and 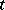 is a
is a 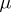 -tableau. Over a field of characteristic zero the Specht modules give precisely all the different absolutely-irreducible representations of
-tableau. Over a field of characteristic zero the Specht modules give precisely all the different absolutely-irreducible representations of 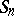 . By Young's rule, the number of times that the Specht module
. By Young's rule, the number of times that the Specht module 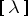 over $\mathbf{Q}$ occurs (as a composition factor) in $\rho(\kappa)$ is equal to the Kostka number $K(\kappa,\lambda)$. If $e_t$ is the Young symmetrizer of a $\mu$-tableau $t$, then the Specht module defined by the underlying diagram is isomorphic to the ideal $F[S_n]e_t$ of $F[S_n]. This is also (up to isomorphism) the representation denoted by $T_{\mu}$ in Representation of the symmetric groups. Cf. Majorization ordering for a number of other results involving partitions, Young diagrams and tableaux, and representations of the symmetric groups.
over $\mathbf{Q}$ occurs (as a composition factor) in $\rho(\kappa)$ is equal to the Kostka number $K(\kappa,\lambda)$. If $e_t$ is the Young symmetrizer of a $\mu$-tableau $t$, then the Specht module defined by the underlying diagram is isomorphic to the ideal $F[S_n]e_t$ of $F[S_n]. This is also (up to isomorphism) the representation denoted by $T_{\mu}$ in Representation of the symmetric groups. Cf. Majorization ordering for a number of other results involving partitions, Young diagrams and tableaux, and representations of the symmetric groups.
References
| [a1] | D. Knuth, "The art of computer programming" , 3 , Addison-Wesley (1973) |
Young tableau. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Young_tableau&oldid=54785