Majorization ordering
Let 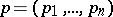 and
and  be
be  -tuples of non-negative real numbers of the same
-tuples of non-negative real numbers of the same 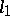 -norm, i.e.
-norm, i.e.
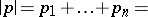 |
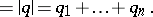 |
Then 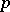 is said to be majorized by
is said to be majorized by 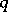 if and only if
if and only if 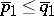 ,
, 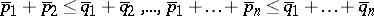 , where
, where 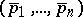 is a reordering of the
is a reordering of the  -tuple
-tuple 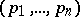 such that
such that 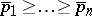 . This defines a partial order which occurs under various names in various parts of mathematics: majority ordering, majorization ordering, specialization ordering, Snapper ordering, Ehresmann ordering, dominance ordering, mixing ordering, natural ordering,
. This defines a partial order which occurs under various names in various parts of mathematics: majority ordering, majorization ordering, specialization ordering, Snapper ordering, Ehresmann ordering, dominance ordering, mixing ordering, natural ordering,  .
.
The symbol 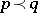 denotes that
denotes that 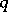 majorizes
majorizes 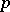 . A few results involving the majorization ordering are as follows.
. A few results involving the majorization ordering are as follows.
If 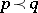 , then for all continuous convex functions
, then for all continuous convex functions 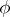 of one variable,
of one variable, 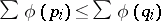 .
.
A matrix 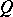 of non-negative real numbers is said to be doubly stochastic if all its rows and all its columns sum to
of non-negative real numbers is said to be doubly stochastic if all its rows and all its columns sum to 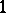 :
: 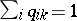 ,
, 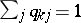 for all
for all 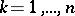 . Then
. Then 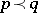 if and only if there is a doubly-stochastic matrix
if and only if there is a doubly-stochastic matrix 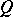 such that
such that 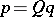 .
.
Let 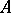 be a Hermitian
be a Hermitian 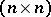 -matrix,
-matrix, 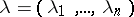 its
its  -tuple of eigen values, and
-tuple of eigen values, and 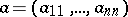 its
its  -tuple of diagonal elements. Then
-tuple of diagonal elements. Then 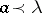 , [a1]. Conversely, if
, [a1]. Conversely, if 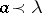 , then there exists a real symmetric
, then there exists a real symmetric 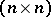 -matrix with eigen values
-matrix with eigen values 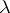 and diagonal elements
and diagonal elements  , [a2], [a3]. The Schur result, [a1], can be reformulated to say that
, [a2], [a3]. The Schur result, [a1], can be reformulated to say that  is in the convex hull of
is in the convex hull of 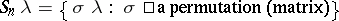 . In this form the result generalizes as follows. Let
. In this form the result generalizes as follows. Let 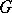 be a compact Lie group with Lie algebra
be a compact Lie group with Lie algebra  ; let
; let 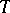 be a maximal torus in
be a maximal torus in 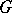 and
and 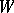 the corresponding Weyl group. Consider the adjoint action of
the corresponding Weyl group. Consider the adjoint action of  on
on 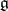 . Then
. Then 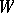 -orbits in
-orbits in 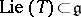 correspond to
correspond to 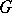 -orbits in
-orbits in 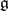 . Fix a
. Fix a 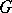 -invariant metric on
-invariant metric on 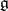 . Then the orthogonal projection of a
. Then the orthogonal projection of a 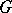 -orbit onto
-orbit onto 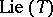 is the convex hull of the corresponding
is the convex hull of the corresponding 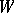 -orbit, [a18]. For a more general result in the context of symplectic geometry cf. [a19].
-orbit, [a18]. For a more general result in the context of symplectic geometry cf. [a19].
A function 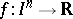 , where
, where 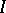 is an open interval in
is an open interval in 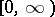 , is said to be Schur convex if
, is said to be Schur convex if 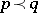 ,
, 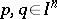 , implies
, implies 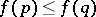 . Then
. Then  is Schur convex if and only if it is symmetric, i.e.
is Schur convex if and only if it is symmetric, i.e. 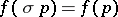 for all permutations
for all permutations 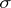 , and
, and
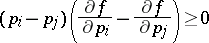 |
for all 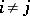 . This condition is often called the Schur condition.
. This condition is often called the Schur condition.
For each  -tuple of non-negative real numbers
-tuple of non-negative real numbers 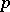 , define a function
, define a function 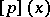 by
by
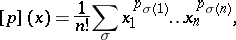 |
where the sum is over all permutations 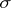 of
of 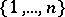 . Then Muirhead's inequality says that
. Then Muirhead's inequality says that 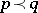 if and only if
if and only if 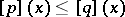 for all
for all  -tuples of non-negative real numbers
-tuples of non-negative real numbers  . The arithmetic-mean geometric-mean inequality corresponds to the special case
. The arithmetic-mean geometric-mean inequality corresponds to the special case 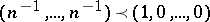 .
.
Let 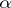 be a partition of
be a partition of  . The corresponding Young subgroup of the symmetric group
. The corresponding Young subgroup of the symmetric group 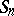 is
is 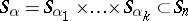 , where
, where 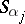 permutes the
permutes the 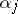 elements
elements  . Let
. Let 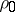 be the trivial representation of
be the trivial representation of 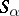 and
and 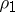 the alternating or sign representation, which assigns to a permutation
the alternating or sign representation, which assigns to a permutation 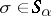 its sign
its sign 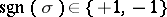 , i.e. if
, i.e. if 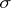 can be written as a product of
can be written as a product of 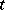 transpositions then
transpositions then 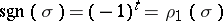 .
.
Let 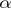 and
and 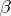 be two partitions of
be two partitions of  , extended with zeros if necessary to make up a vector of length
, extended with zeros if necessary to make up a vector of length  .
.
The Snapper–Liebler–Vitale–Lam–Young theorem says that the representation 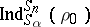 is a subrepresentation of
is a subrepresentation of 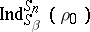 if and only if
if and only if 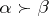 , [a13].
, [a13].
The Rugh–Schönhofer theorem says that the intertwining number 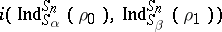 is non-zero if and only if
is non-zero if and only if 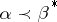 . Here
. Here 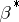 is the dual partition (conjugate partition) of
is the dual partition (conjugate partition) of 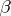 , i.e.
, i.e. 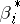 is the number of elements in
is the number of elements in 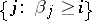 , [a10].
, [a10].
The Gale–Ryser theorem says that there exists a matrix of zeros and ones whose rows sum to the vector 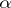 and whose columns sum to the vector
and whose columns sum to the vector 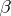 if and only if
if and only if 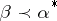 (or, equivalently,
(or, equivalently, 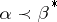 ), [a12].
), [a12].
Consider the space 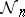 of all complex nilpotent
of all complex nilpotent 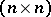 -matrices. Let
-matrices. Let 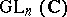 act on
act on 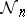 by similarity, and for each partition
by similarity, and for each partition 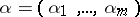 of
of  , let
, let 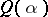 be the orbit containing the Jordan matrix with Jordan blocks of size
be the orbit containing the Jordan matrix with Jordan blocks of size 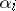 and zero eigen value. Then the Gerstenhaber–Hesselink theorem says that the closure of an orbit
and zero eigen value. Then the Gerstenhaber–Hesselink theorem says that the closure of an orbit 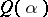 contains an orbit
contains an orbit 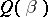 ,
,  , if and only if
, if and only if 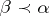 , [a6].
, [a6].
Let 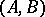 be a pair consisting of an
be a pair consisting of an 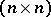 -matrix
-matrix 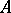 and an
and an  -matrix
-matrix 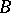 . The pair
. The pair 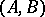 is called completely reachable if the column vectors of the matrices
is called completely reachable if the column vectors of the matrices 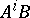 ,
, 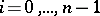 , span all of
, span all of 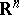 . This is equivalent to the property that in the linear control system
. This is equivalent to the property that in the linear control system 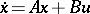 the origin can be steered to any point in
the origin can be steered to any point in 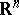 by suitable controls
by suitable controls 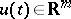 . The Kronecker indices or controllability indices of a completely-reachable pair
. The Kronecker indices or controllability indices of a completely-reachable pair 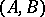 are defined as follows. Let
are defined as follows. Let 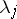 be the dimension of the space spanned by the column vectors of
be the dimension of the space spanned by the column vectors of 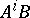 ,
, 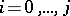 . Let
. Let 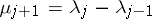 ,
, 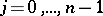 ,
, 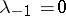 ,
, 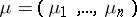 . Then the Kronecker indices
. Then the Kronecker indices 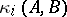 of
of 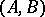 are the elements of the partition
are the elements of the partition 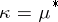 dual to
dual to 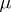 . (This concept of a Kronecker index should not be confused with the Kronecker index of a function at a point, cf. Lefschetz formula). The partition
. (This concept of a Kronecker index should not be confused with the Kronecker index of a function at a point, cf. Lefschetz formula). The partition 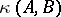 is invariant under the following transformations of
is invariant under the following transformations of 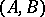 :
: 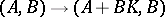 , where
, where 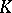 is an arbitrary
is an arbitrary 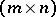 -matrix;
-matrix;  , where
, where 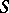 is an invertible
is an invertible 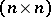 -matrix; and
-matrix; and 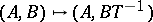 , where
, where 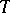 is an invertible
is an invertible 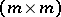 -matrix. Together these transformations make up the feedback group (of the control system
-matrix. Together these transformations make up the feedback group (of the control system 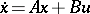 ) and the Brunowski–Kalman–Morse–Wonham theorem says that
) and the Brunowski–Kalman–Morse–Wonham theorem says that 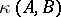 is a complex invariant of the action of the feedback group, i.e. the orbits of the action are labelled by partitions of
is a complex invariant of the action of the feedback group, i.e. the orbits of the action are labelled by partitions of  . Moreover, the closure
. Moreover, the closure  of the orbit labelled by
of the orbit labelled by 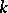 contains the orbit
contains the orbit 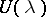 if and only if
if and only if 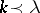 , [a6].
, [a6].
Let 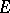 be a holomorphic vector bundle (cf. also Vector bundle, analytic) over the Riemann sphere
be a holomorphic vector bundle (cf. also Vector bundle, analytic) over the Riemann sphere 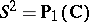 . Then by Grothendieck's theorem,
. Then by Grothendieck's theorem, 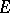 splits as a direct sum of complex line bundles
splits as a direct sum of complex line bundles 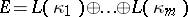 , where
, where 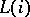 is the unique (up to isomorphism) complex line bundle of first Chern number
is the unique (up to isomorphism) complex line bundle of first Chern number 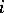 . Now consider a holomorphic family of complex vector bundles
. Now consider a holomorphic family of complex vector bundles 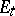 over
over 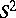 . Then by Shatz' theorem,
. Then by Shatz' theorem, 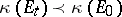 for
for 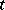 small enough, and, conversely, if
small enough, and, conversely, if 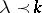 , then there is a holomorphic family such that
, then there is a holomorphic family such that 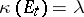 for
for 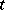 small and
small and 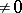 and
and 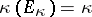 .
.
All these manifestations of the majorization order are far from unrelated, cf. [a4], [a6], [a9]. There are generalizations of certain of the theorems above to the case of other Weyl groups (than 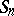 ) and relations with the Bruhat ordering on the Weyl group defined by the inclusions
) and relations with the Bruhat ordering on the Weyl group defined by the inclusions 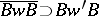 of the closure of the parts of the Bruhat decomposition
of the closure of the parts of the Bruhat decomposition  of a simple Lie group, [a5], [a7].
of a simple Lie group, [a5], [a7].
Let 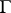 be a directed graph (cf. Graph, oriented). For a vertex
be a directed graph (cf. Graph, oriented). For a vertex  , let the out-degree (demi-degree outwards),
, let the out-degree (demi-degree outwards), 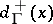 , be defined as the number of arcs starting in
, be defined as the number of arcs starting in  , and the in-degree (demi-degree inwards),
, and the in-degree (demi-degree inwards), 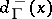 , as the number of arcs terminating in
, as the number of arcs terminating in  . The degree at
. The degree at  ,
, 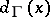 , is
, is 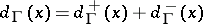 . A
. A 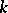 -graph is a graph with
-graph is a graph with 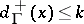 for all vertices
for all vertices  . Let
. Let 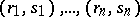 be pairs of elements of
be pairs of elements of 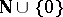 and
and 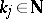 . Define
. Define 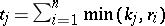 . Then there exists a graph
. Then there exists a graph 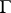 with
with 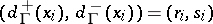 if and only if
if and only if 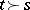 in the majorization ordering, [a17].
in the majorization ordering, [a17].
References
| [a1] | I. Schur, "Ueber ein Klasse von Mittelbildungen mit Anwendungen auf der Determinantentheorie" Sitzungsber. Berliner Math. Ges. , 22 (1923) pp. 9–20 |
| [a2] | A. Horn, "Doubly stochastic matrices and the diagonal of a rotation matrix" Amer. J. Math. , 76 (1954) pp. 620–630 |
| [a3] | L. Mirsky, "Matrices with prescribed characteristic roots and diagonal elements" J. London Math. Soc. , 33 (1958) pp. 14–21 |
| [a4] | A.W. Marshall, J. Olkin, "Inequalities: majorization and its applications" , Acad. Press (1979) |
| [a5] | H.-P. Kraft, "Conjugacy classes and Weyl group representations" Astérisque , 87/88 (1981) pp. 191–206 |
| [a6] | M. Hazewinkel, C.F. Martin, "Representations of the symmetric group, the specialization order, systems, and Grassmann manifolds" Enseign. Math. , 29 (1983) pp. 53–87 |
| [a7] | C. de Cocini, C. Procesi, "Symmetric functions, conjugacy classes and the flag variety" Invent. Math. , 64 (1981) pp. 203–220 |
| [a8] | G.H. Hardy, J.E. Littlewood, G. Pólya, "Inequalities" , Cambridge Univ. Press (1952) |
| [a9] | A. Kerber, "The diagram lattice as structural principle in mathematics" P. Kramer (ed.) A. Rieckers (ed.) , Group Theoretical Methods in Physics (Tübingen, 1977) , Springer (1978) pp. 53–71 |
| [a10] | A. Mead, E. Ruch, A. Schönhofer, "Theory of chirality functions, generalized for molecules with chiral ligands" Theor. Chin. Acta , 29 (1973) pp. 269–304 |
| [a11] | D.S. Mitrinović, J.E. Pečarić, V. Volenec, "Recent advances in geometric inequalities" , Kluwer (1989) |
| [a12] | H.J. Ryser, "Combinatorial mathematics" , Math. Assoc. Amer. (1963) |
| [a13] | R.A. Liebler, M.R. Vitale, "Ordering the partition characters of the symmetric group" J. of Algebra , 25 (1973) pp. 487–489 |
| [a14] | J.G. Macdonald, "Symmetric functions and Hall polynomials" , Oxford Univ. Press (1979) |
| [a15] | P.S. Bullen, D.S. Mitrinović, P.M. Vasić, "Means and their inequalities" , Reidel (1988) |
| [a16] | T. Brylawski, "The lattice of integer partitions" Discrete Math. , 6 (1973) pp. 201–209 |
| [a17] | C. Berge, "Graphs et hypergraphes" , Dunod (1970) pp. Chapt. 6 |
| [a18] | B. Kostant, "On convexity, the Weyl group and the Iwasawa decomposition" Ann. Sci. Ec. Norm. Sup. , 6 (1973) pp. 413–455 |
| [a19] | M.F. Atiyah, "Convexity and commuting Hamiltonians" Bull. London Math. Soc. , 14 (1982) pp. 1–15 |
Majorization ordering. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Majorization_ordering&oldid=39850