Difference between revisions of "Halin graph"
(add MSC link) |
(svg picture) |
||
| Line 1: | Line 1: | ||
{{TEX|done}} | {{TEX|done}} | ||
{{MSC|05C}} | {{MSC|05C}} | ||
| + | |||
In work dealing generally with properties of minimal connectivity in graphs (cf. [[Graph, connectivity of a|Graph, connectivity of a]]), R. Halin [[#References|[a4]]] suggested the following construction: Let $T$ be a finite [[Tree|tree]] having no vertices of degree $2$. Now, imbed $T$ in the plane (cf. [[Graph imbedding|Graph imbedding]]) and add edges to form a [[Cycle|cycle]], $C$, through any and all of the degree-$1$ vertices of $T$ and in such a way that the resulting graph $G$ is planar (cf. [[Graph, planar|Graph, planar]]). Such structures are nowadays referred to as Halin graphs. Indeed, the construction just described yields an example of a class of edge-minimal planar $3$-connected graphs. The graph shown below is Halin. | In work dealing generally with properties of minimal connectivity in graphs (cf. [[Graph, connectivity of a|Graph, connectivity of a]]), R. Halin [[#References|[a4]]] suggested the following construction: Let $T$ be a finite [[Tree|tree]] having no vertices of degree $2$. Now, imbed $T$ in the plane (cf. [[Graph imbedding|Graph imbedding]]) and add edges to form a [[Cycle|cycle]], $C$, through any and all of the degree-$1$ vertices of $T$ and in such a way that the resulting graph $G$ is planar (cf. [[Graph, planar|Graph, planar]]). Such structures are nowadays referred to as Halin graphs. Indeed, the construction just described yields an example of a class of edge-minimal planar $3$-connected graphs. The graph shown below is Halin. | ||
| − | + | [[File:Halin graph.svg|center|300px|Halin graph]] | |
| − | |||
| − | |||
| − | Tree edges in | + | Tree edges in green. |
It is easy to check whether or not an arbitrary planar graph is Halin, since every planar $3$-connected graph is uniquely (up to the specification of the infinite face) imbeddable in the plane. In fact, the naive approach works in that one need only check whether the graph is $3$-connected, then imbed it in the plane and look for a face in the graph such that the edges defining the face, if removed, leave a tree without degree-$2$ vertices. This recognizability attribute is relevant since it is known that Halin graphs are contained in a so-called $3$-terminal recursive class. As shown in [[#References|[a3]]], this suffices to guarantee linear-time algorithms for many otherwise hard graph problems when instances are confined to Halin graphs (e.g. vertex cover, dominating set, chromatic number, minimum-maximal matching, etc.). | It is easy to check whether or not an arbitrary planar graph is Halin, since every planar $3$-connected graph is uniquely (up to the specification of the infinite face) imbeddable in the plane. In fact, the naive approach works in that one need only check whether the graph is $3$-connected, then imbed it in the plane and look for a face in the graph such that the edges defining the face, if removed, leave a tree without degree-$2$ vertices. This recognizability attribute is relevant since it is known that Halin graphs are contained in a so-called $3$-terminal recursive class. As shown in [[#References|[a3]]], this suffices to guarantee linear-time algorithms for many otherwise hard graph problems when instances are confined to Halin graphs (e.g. vertex cover, dominating set, chromatic number, minimum-maximal matching, etc.). | ||
Latest revision as of 20:45, 16 March 2023
2020 Mathematics Subject Classification: Primary: 05C [MSN][ZBL]
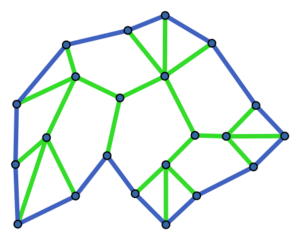
In work dealing generally with properties of minimal connectivity in graphs (cf. Graph, connectivity of a), R. Halin [a4] suggested the following construction: Let $T$ be a finite tree having no vertices of degree $2$. Now, imbed $T$ in the plane (cf. Graph imbedding) and add edges to form a cycle, $C$, through any and all of the degree-$1$ vertices of $T$ and in such a way that the resulting graph $G$ is planar (cf. Graph, planar). Such structures are nowadays referred to as Halin graphs. Indeed, the construction just described yields an example of a class of edge-minimal planar $3$-connected graphs. The graph shown below is Halin.
Tree edges in green.
It is easy to check whether or not an arbitrary planar graph is Halin, since every planar $3$-connected graph is uniquely (up to the specification of the infinite face) imbeddable in the plane. In fact, the naive approach works in that one need only check whether the graph is $3$-connected, then imbed it in the plane and look for a face in the graph such that the edges defining the face, if removed, leave a tree without degree-$2$ vertices. This recognizability attribute is relevant since it is known that Halin graphs are contained in a so-called $3$-terminal recursive class. As shown in [a3], this suffices to guarantee linear-time algorithms for many otherwise hard graph problems when instances are confined to Halin graphs (e.g. vertex cover, dominating set, chromatic number, minimum-maximal matching, etc.).
There are other interesting properties of Halin graphs. First, all Halin graphs possess Hamiltonian cycles. In fact, they are $1$-Hamiltonian in that they are Hamiltonian and if any vertex is removed, the resulting graph remains Hamiltonian [a1]. Even-order Halin graphs are bicritical in that the deletion of any two vertices leaves a graph that possesses a one-factor [a6], and Halin graphs are "pancyclic graphalmost pancyclic" in that for any such graph of order $n$, every cycle of length $3\leq t\leq n$ is present with the possible exception of one of even length [a2]. Thus Halin graphs are not bipartite (cf. Graph, bipartite).
Halin graphs are class-$1$ graphs in that their chromatic index is always exactly the same as the maximum vertex degree in the graph [a5]. Also, it is clear that a Halin graph may have more than one correct bipartition of its edge set (yielding the desired cycle and tree). Denoting these by $\{T_1,C_1\},\dots,\{T_k,C_k\}$; then, given any pair of distinct cycles $C_i$ and $C_j$, the $T_i$ and $T_j$ are isomorphic [a5].
While being a Halin graph is polynomially verifiable, deciding if a given graph possesses a spanning subgraph that is Halin is $\mathcal{NP}$-complete (cf. Complexity theory). Similarly, deciding whether a graph is a subgraph of some Halin graph is also $\mathcal{NP}$-complete, [a5].
References
| [a1] | J.A. Bondy, "Pancyclic graphs: recent results" , Infinite and Finite Sets 1 , Colloq. Math. Soc. Janos Bolyai , 10 , North-Holland (1975) pp. 181–187 |
| [a2] | J.A. Bondy, L. Lovász, "Length of cycles in Halin graphs" J. Graph Th. , 8 (1985) pp. 397–410 |
| [a3] | R.B. Borie, R.G. Parker, C.A. Tovey, "Automatic generation of linear-time algorithms from predicate calculus descriptions of problems on recursively constructed graph families" Algorithmica , 7 (1992) pp. 555–581 |
| [a4] | R. Halin, "Studies on minimally  -connected graphs" D.J.A. Welsh (ed.) , Combinatorial Mathematics and Its Applications , Acad. Press (1971) pp. 129–136 -connected graphs" D.J.A. Welsh (ed.) , Combinatorial Mathematics and Its Applications , Acad. Press (1971) pp. 129–136 |
| [a5] | S.B. Horton, R.G. Parker, R.B. Borie, "On some results pertaining to Halin graphs" Congressus Numerantium , 93 (1992) pp. 65–87 |
| [a6] | L. Lovász, M.D. Plummer, "On a family of planar bicritical graphs" Proc. London Math. Soc. , 30 (1975) pp. 160–175 |
Halin graph. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Halin_graph&oldid=52734