Difference between revisions of "Alperin conjecture"
Ulf Rehmann (talk | contribs) m (typos) |
m (fixing spaces) |
||
| Line 14: | Line 14: | ||
Modular representation theory of finite groups is the study of representations of groups over fields of finite characteristic (cf. also [[Finite group, representation of a|Finite group, representation of a]]; [[Finite group|Finite group]]; [[Field|Field]]). This theory was first developed by R. Brauer, who was motivated largely by a wish to obtain information about complex characters of finite groups (cf. [[Character of a group|Character of a group]]). One of the central themes of Brauer's work was that many representation-theoretic invariants of finite groups should be "locally" determined. When $ p $ | Modular representation theory of finite groups is the study of representations of groups over fields of finite characteristic (cf. also [[Finite group, representation of a|Finite group, representation of a]]; [[Finite group|Finite group]]; [[Field|Field]]). This theory was first developed by R. Brauer, who was motivated largely by a wish to obtain information about complex characters of finite groups (cf. [[Character of a group|Character of a group]]). One of the central themes of Brauer's work was that many representation-theoretic invariants of finite groups should be "locally" determined. When $ p $ | ||
| − | is a prime number, a $ p $- | + | is a prime number, a $ p $-local subgroup of a finite group is the normalizer (cf. also [[Normalizer of a subset|Normalizer of a subset]]) of a non-trivial $ p $-subgroup of that group. An important feature of Alperin's weight conjecture is that it makes a precise prediction as to how a fundamental representation-theoretic invariant should be $ p $-locally controlled. |
| − | local subgroup of a finite group is the normalizer (cf. also [[Normalizer of a subset|Normalizer of a subset]]) of a non-trivial $ p $- | ||
| − | subgroup of that group. An important feature of Alperin's weight conjecture is that it makes a precise prediction as to how a fundamental representation-theoretic invariant should be $ p $- | ||
| − | locally controlled. | ||
Let $ F $ | Let $ F $ | ||
| Line 25: | Line 22: | ||
where the $ B _ {i} $' | where the $ B _ {i} $' | ||
s are mutually annihilating indecomposable two-sided ideals (cf. [[Ideal|Ideal]]). The $ B _ {i} $' | s are mutually annihilating indecomposable two-sided ideals (cf. [[Ideal|Ideal]]). The $ B _ {i} $' | ||
| − | s are known as blocks of $ FG $( | + | s are known as blocks of $ FG $ (cf. also [[Block|Block]]). Let $ l ( B _ {i} ) $ |
| − | cf. also [[Block|Block]]). Let $ l ( B _ {i} ) $ | + | denote the number of isomorphism types of simple $ B _ {i} $-modules, and $ l ( FG ) = \sum _ {i = 1 } ^ {m} l ( B _ {i} ) $. |
| − | denote the number of isomorphism types of simple $ B _ {i} $- | ||
| − | modules, and $ l ( FG ) = \sum _ {i = 1 } ^ {m} l ( B _ {i} ) $. | ||
It is sometimes the case that $ B _ {i} $ | It is sometimes the case that $ B _ {i} $ | ||
is isomorphic to a full matrix algebra over $ F $. | is isomorphic to a full matrix algebra over $ F $. | ||
In that case, $ B _ {i} $ | In that case, $ B _ {i} $ | ||
is a block of defect zero of $ FG $. | is a block of defect zero of $ FG $. | ||
| − | Such blocks have special significance; they are in bijection with the isomorphism types of projective simple $ FG $- | + | Such blocks have special significance; they are in bijection with the isomorphism types of projective simple $ FG $-modules. Blocks other than blocks of defect zero are said to have positive defect. |
| − | modules. Blocks other than blocks of defect zero are said to have positive defect. | ||
A weight of $ FG $ | A weight of $ FG $ | ||
is a pair $ ( Q,S ) $, | is a pair $ ( Q,S ) $, | ||
where $ Q $ | where $ Q $ | ||
| − | is a (possibly trivial) $ p $- | + | is a (possibly trivial) $ p $-subgroup (cf. also [[P-group| $ p $-group]]) of $ G $ |
| − | subgroup (cf. also [[P-group| $ p $- | ||
| − | group]]) of $ G $ | ||
and $ S $ | and $ S $ | ||
| − | is a projective simple $ FN _ {G} ( Q ) /Q $- | + | is a projective simple $ FN _ {G} ( Q ) /Q $-module. Weights $ ( Q,S ) $ |
| − | module. Weights $ ( Q,S ) $ | ||
and $ ( R,T ) $ | and $ ( R,T ) $ | ||
are deemed to be equivalent if for some $ x \in G $ | are deemed to be equivalent if for some $ x \in G $ | ||
one has $ Q ^ {x} = R $ | one has $ Q ^ {x} = R $ | ||
and $ S ^ {x} \cong T $ | and $ S ^ {x} \cong T $ | ||
| − | as $ FN _ {G} ( R ) /R $- | + | as $ FN _ {G} ( R ) /R $-modules. The "non-blockwise" version of Alperin's weight conjecture simply asserts that the number of isomorphism types of simple $ FG $-modules should equal the number of equivalence classes of weights of $ FG $. |
| − | modules. The "non-blockwise" version of Alperin's weight conjecture simply asserts that the number of isomorphism types of simple $ FG $- | ||
| − | modules should equal the number of equivalence classes of weights of $ FG $. | ||
The number of equivalence classes of weights of the form $ ( \{ 1 _ {G} \} ,S ) $ | The number of equivalence classes of weights of the form $ ( \{ 1 _ {G} \} ,S ) $ | ||
| − | is just the number of isomorphism types of projective simple $ FG $- | + | is just the number of isomorphism types of projective simple $ FG $-modules, and the number of equivalence classes of weights of the form $ ( Q,S ) $ |
| − | modules, and the number of equivalence classes of weights of the form $ ( Q,S ) $ | ||
with $ Q \neq \{ 1 _ {G} \} $ | with $ Q \neq \{ 1 _ {G} \} $ | ||
| − | is determined within $ p $- | + | is determined within $ p $-local subgroups. |
| − | local subgroups. | ||
To describe the "blockwise" version of the conjecture one has to assign weights to blocks. This is achieved by means of the [[Brauer homomorphism|Brauer homomorphism]]. When $ Q $ | To describe the "blockwise" version of the conjecture one has to assign weights to blocks. This is achieved by means of the [[Brauer homomorphism|Brauer homomorphism]]. When $ Q $ | ||
| − | is a $ p $- | + | is a $ p $-subgroup of $ G $, |
| − | subgroup of $ G $, | ||
the projection $ { { \mathop{\rm br} } _ {Q} } : {FG } \rightarrow {FC _ {G} ( Q ) } $ | the projection $ { { \mathop{\rm br} } _ {Q} } : {FG } \rightarrow {FC _ {G} ( Q ) } $ | ||
with kernel $ F [ G \backslash C _ {G} ( Q ) ] $ | with kernel $ F [ G \backslash C _ {G} ( Q ) ] $ | ||
| − | restricts to an algebra homomorphism from the fixed-point subalgebra $ FG ^ {Q} $( | + | restricts to an algebra homomorphism from the fixed-point subalgebra $ FG ^ {Q} $ (under conjugation by $ Q $) |
| − | under conjugation by $ Q $) | ||
onto $ FC _ {G} ( Q ) $. | onto $ FC _ {G} ( Q ) $. | ||
Given a weight $ ( Q,S ) $, | Given a weight $ ( Q,S ) $, | ||
one may view $ S $ | one may view $ S $ | ||
| − | as an $ FN _ {G} ( Q ) $- | + | as an $ FN _ {G} ( Q ) $-module. One assigns the weight $ ( Q,S ) $ |
| − | module. One assigns the weight $ ( Q,S ) $ | ||
to the block $ B $ | to the block $ B $ | ||
if and only if $ 1 _ {B} { \mathop{\rm br} } _ {Q} $ | if and only if $ 1 _ {B} { \mathop{\rm br} } _ {Q} $ | ||
| Line 82: | Line 66: | ||
this is evidently true. If $ B $ | this is evidently true. If $ B $ | ||
is of positive defect, then the conjecture makes a prediction that $ l ( B ) $ | is of positive defect, then the conjecture makes a prediction that $ l ( B ) $ | ||
| − | is $ p $- | + | is $ p $-locally determined in a precise manner, since no weights of the form $ ( \{ 1 _ {G} \} , S ) $ |
| − | locally determined in a precise manner, since no weights of the form $ ( \{ 1 _ {G} \} , S ) $ | ||
are then assigned to $ B $. | are then assigned to $ B $. | ||
| Line 93: | Line 76: | ||
Given a chain $ \sigma $ | Given a chain $ \sigma $ | ||
| − | of strictly increasing $ p $- | + | of strictly increasing $ p $-subgroups of $ G $, |
| − | subgroups of $ G $, | ||
say $ \sigma = Q _ {1} < Q _ {2} < \dots < Q _ {n} $, | say $ \sigma = Q _ {1} < Q _ {2} < \dots < Q _ {n} $, | ||
one sets $ G _ \sigma = \cap _ {i = 1 } ^ {n} N _ {G} ( Q _ {i} ) $, | one sets $ G _ \sigma = \cap _ {i = 1 } ^ {n} N _ {G} ( Q _ {i} ) $, | ||
| Line 110: | Line 92: | ||
where $ \Delta _ {p} $ | where $ \Delta _ {p} $ | ||
| − | denotes the collection of all such chains of $ p $- | + | denotes the collection of all such chains of $ p $-subgroups of $ G $ (including the empty chain). Thus, $ k ( B ) $ |
| − | subgroups of $ G $( | + | (the contribution to the alternating sum from the empty chain) is predicted to be $ p $-locally controlled in a precise fashion. |
| − | including the empty chain). Thus, $ k ( B ) $ | ||
| − | (the contribution to the alternating sum from the empty chain) is predicted to be $ p $- | ||
| − | locally controlled in a precise fashion. | ||
| − | J. Thévenaz has given a reformulation of Alperin's conjecture which is expressed in terms of equivariant [[K-theory| $ K $- | + | J. Thévenaz has given a reformulation of Alperin's conjecture which is expressed in terms of equivariant [[K-theory| $ K $-theory]]. E.C. Dade has continued the pattern of predictions of precise $ p $-local control of representation-theoretic invariants by making a series of conjectures expressing the number of irreducible characters of defect $ d $ |
| − | theory]]. E.C. Dade has continued the pattern of predictions of precise $ p $- | ||
| − | local control of representation-theoretic invariants by making a series of conjectures expressing the number of irreducible characters of defect $ d $ | ||
assigned to a block $ B $ | assigned to a block $ B $ | ||
of $ FG $ | of $ FG $ | ||
Revision as of 08:59, 18 August 2022
Alperin weight conjecture
Modular representation theory of finite groups is the study of representations of groups over fields of finite characteristic (cf. also Finite group, representation of a; Finite group; Field). This theory was first developed by R. Brauer, who was motivated largely by a wish to obtain information about complex characters of finite groups (cf. Character of a group). One of the central themes of Brauer's work was that many representation-theoretic invariants of finite groups should be "locally" determined. When $ p $ is a prime number, a $ p $-local subgroup of a finite group is the normalizer (cf. also Normalizer of a subset) of a non-trivial $ p $-subgroup of that group. An important feature of Alperin's weight conjecture is that it makes a precise prediction as to how a fundamental representation-theoretic invariant should be $ p $-locally controlled.
Let $ F $ be an algebraically closed field of prime characteristic $ p $, and let $ G $ be a finite group. Then the group algebra has a unique decomposition in the form $ FG = B _ {1} \oplus \dots \oplus B _ {m} $, where the $ B _ {i} $' s are mutually annihilating indecomposable two-sided ideals (cf. Ideal). The $ B _ {i} $' s are known as blocks of $ FG $ (cf. also Block). Let $ l ( B _ {i} ) $ denote the number of isomorphism types of simple $ B _ {i} $-modules, and $ l ( FG ) = \sum _ {i = 1 } ^ {m} l ( B _ {i} ) $. It is sometimes the case that $ B _ {i} $ is isomorphic to a full matrix algebra over $ F $. In that case, $ B _ {i} $ is a block of defect zero of $ FG $. Such blocks have special significance; they are in bijection with the isomorphism types of projective simple $ FG $-modules. Blocks other than blocks of defect zero are said to have positive defect.
A weight of $ FG $ is a pair $ ( Q,S ) $, where $ Q $ is a (possibly trivial) $ p $-subgroup (cf. also $ p $-group) of $ G $ and $ S $ is a projective simple $ FN _ {G} ( Q ) /Q $-module. Weights $ ( Q,S ) $ and $ ( R,T ) $ are deemed to be equivalent if for some $ x \in G $ one has $ Q ^ {x} = R $ and $ S ^ {x} \cong T $ as $ FN _ {G} ( R ) /R $-modules. The "non-blockwise" version of Alperin's weight conjecture simply asserts that the number of isomorphism types of simple $ FG $-modules should equal the number of equivalence classes of weights of $ FG $. The number of equivalence classes of weights of the form $ ( \{ 1 _ {G} \} ,S ) $ is just the number of isomorphism types of projective simple $ FG $-modules, and the number of equivalence classes of weights of the form $ ( Q,S ) $ with $ Q \neq \{ 1 _ {G} \} $ is determined within $ p $-local subgroups.
To describe the "blockwise" version of the conjecture one has to assign weights to blocks. This is achieved by means of the Brauer homomorphism. When $ Q $ is a $ p $-subgroup of $ G $, the projection $ { { \mathop{\rm br} } _ {Q} } : {FG } \rightarrow {FC _ {G} ( Q ) } $ with kernel $ F [ G \backslash C _ {G} ( Q ) ] $ restricts to an algebra homomorphism from the fixed-point subalgebra $ FG ^ {Q} $ (under conjugation by $ Q $) onto $ FC _ {G} ( Q ) $. Given a weight $ ( Q,S ) $, one may view $ S $ as an $ FN _ {G} ( Q ) $-module. One assigns the weight $ ( Q,S ) $ to the block $ B $ if and only if $ 1 _ {B} { \mathop{\rm br} } _ {Q} $ does not annihilate $ S $. The "blockwise" version of Alperin's weight conjecture predicts that for each block $ B $ of $ FG $, $ l ( B ) $ should equal the number of equivalence classes of weights assigned to $ B $. If $ B $ is of defect $ 0 $, this is evidently true. If $ B $ is of positive defect, then the conjecture makes a prediction that $ l ( B ) $ is $ p $-locally determined in a precise manner, since no weights of the form $ ( \{ 1 _ {G} \} , S ) $ are then assigned to $ B $.
Another interpretation of Alperin's weight conjecture has been given by R. Knörr and G.R. Robinson. Given a block $ B $, Brauer showed how to assign complex irreducible characters to $ B $, and the number of such characters assigned to $ B $ is $ { \mathop{\rm dim} } _ {F} ( Z ( B ) ) $, denoted $ k ( B ) $.
Given a chain $ \sigma $ of strictly increasing $ p $-subgroups of $ G $, say $ \sigma = Q _ {1} < Q _ {2} < \dots < Q _ {n} $, one sets $ G _ \sigma = \cap _ {i = 1 } ^ {n} N _ {G} ( Q _ {i} ) $, and $ | \sigma | = n $. Then one sets $ B _ \sigma = ( 1 _ {B} { \mathop{\rm br} } _ {Q _ {n} } ) \cdot FG _ \sigma $, which is a sum of certain blocks of the group algebra $ FG _ \sigma $. Then the blockwise version of Alperin's weight conjecture is equivalent to the assertion that whenever $ B $ is a block of positive defect of $ FG $ for some finite group $ G $, then
$$ \sum _ {\sigma \in \Delta _ {p} /G } ( -1 ) ^ {\left | \sigma \right | } k ( B _ \sigma ) = 0, $$
where $ \Delta _ {p} $ denotes the collection of all such chains of $ p $-subgroups of $ G $ (including the empty chain). Thus, $ k ( B ) $ (the contribution to the alternating sum from the empty chain) is predicted to be $ p $-locally controlled in a precise fashion.
J. Thévenaz has given a reformulation of Alperin's conjecture which is expressed in terms of equivariant $ K $-theory. E.C. Dade has continued the pattern of predictions of precise $ p $-local control of representation-theoretic invariants by making a series of conjectures expressing the number of irreducible characters of defect $ d $ assigned to a block $ B $ of $ FG $ as an alternating sum somewhat similar to that above. An irreducible character $ \chi $ is said to have defect $ d $ for the prime number $ p $ if $ p ^ {d} \| { {| G | } / {\chi ( 1 ) } } $. Dade's conjectures may be viewed as unifying and extending Alperin's weight conjecture and the Alperin–McKay conjecture. Furthermore, they are compatible with techniques of Clifford theory and offer the prospect of reducing these questions to questions about finite simple groups (cf. Simple finite group).
References
| [a1] | J.L. Alperin, "Weights for finite groups" , Proc. Symp. Pure Math. , 47 , Amer. Math. Soc. (1987) pp. 369–379 MR0933373 Zbl 0657.20013 |
| [a2] | E.C. Dade, "Counting characters in blocks I" Invent. Math. , 109 (1992) pp. 187–210 MR1168370 Zbl 0738.20011 |
| [a3] | E.C. Dade, "Counting characters in blocks II" J. Reine Angew. Math. , 448 (1994) pp. 97–190 MR1266748 Zbl 0790.20020 |
| [a4] | R. Knörr, G.R. Robinson, "Some remarks on a conjecture of Alperin" J. London Math. Soc. (2) , 39 (1989) pp. 48–60 MR0989918 Zbl 0672.20005 |
| [a5] | J. Thévenaz, "Equivariant 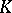 -theory and Alperin's conjecture" J. Pure Appl. Algebra , 85 (1993) pp. 185–202 MR1207508 -theory and Alperin's conjecture" J. Pure Appl. Algebra , 85 (1993) pp. 185–202 MR1207508 |
Alperin conjecture. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Alperin_conjecture&oldid=52516