Difference between revisions of "Weil bundle"
m (AUTOMATIC EDIT (latexlist): Replaced 106 formulas out of 108 by TEX code with an average confidence of 2.0 and a minimal confidence of 2.0.) |
m (Automatically changed introduction) |
||
| Line 2: | Line 2: | ||
the semi-automatic procedure described at https://encyclopediaofmath.org/wiki/User:Maximilian_Janisch/latexlist | the semi-automatic procedure described at https://encyclopediaofmath.org/wiki/User:Maximilian_Janisch/latexlist | ||
was used. | was used. | ||
| − | If the TeX and formula formatting is correct, please remove this message and the {{TEX|semi-auto}} category. | + | If the TeX and formula formatting is correct and if all png images have been replaced by TeX code, please remove this message and the {{TEX|semi-auto}} category. |
Out of 108 formulas, 106 were replaced by TEX code.--> | Out of 108 formulas, 106 were replaced by TEX code.--> | ||
| − | {{TEX|semi-auto}}{{TEX| | + | {{TEX|semi-auto}}{{TEX|part}} |
Consider a [[Weil algebra|Weil algebra]] $A$ and a homomorphism $\varphi \in \operatorname{Hom}( C ^ { \infty } ( \mathbf{R} ^ { m } , \mathbf{R} ) , A )$. A quite simple argument shows that the kernel of each such $\varphi$ contains the ideal of all functions vanishing up to some order <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/w/w120/w120060/w1200604.png"/>, at a unique point $x _ { 0 } \in \mathbf{R} ^ { m }$, cf. [[#References|[a3]]], 35.8. Then evaluation at the Taylor series of order $k$ reveals that $\varphi$ is completely determined by its values on the coordinate functions centred at this point $x _ { 0 }$. Thus, | Consider a [[Weil algebra|Weil algebra]] $A$ and a homomorphism $\varphi \in \operatorname{Hom}( C ^ { \infty } ( \mathbf{R} ^ { m } , \mathbf{R} ) , A )$. A quite simple argument shows that the kernel of each such $\varphi$ contains the ideal of all functions vanishing up to some order <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/w/w120/w120060/w1200604.png"/>, at a unique point $x _ { 0 } \in \mathbf{R} ^ { m }$, cf. [[#References|[a3]]], 35.8. Then evaluation at the Taylor series of order $k$ reveals that $\varphi$ is completely determined by its values on the coordinate functions centred at this point $x _ { 0 }$. Thus, | ||
Revision as of 17:43, 1 July 2020
Consider a Weil algebra $A$ and a homomorphism $\varphi \in \operatorname{Hom}( C ^ { \infty } ( \mathbf{R} ^ { m } , \mathbf{R} ) , A )$. A quite simple argument shows that the kernel of each such $\varphi$ contains the ideal of all functions vanishing up to some order 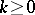 , at a unique point $x _ { 0 } \in \mathbf{R} ^ { m }$, cf. [a3], 35.8. Then evaluation at the Taylor series of order $k$ reveals that $\varphi$ is completely determined by its values on the coordinate functions centred at this point $x _ { 0 }$. Thus,
, at a unique point $x _ { 0 } \in \mathbf{R} ^ { m }$, cf. [a3], 35.8. Then evaluation at the Taylor series of order $k$ reveals that $\varphi$ is completely determined by its values on the coordinate functions centred at this point $x _ { 0 }$. Thus,
\begin{equation*} \operatorname{Hom}( C ^ { \infty } ( \mathbf{R} ^ { m } , \mathbf{R} ) , A ) \simeq A ^ { m } = T _ { A } \mathbf{R} ^ { m }. \end{equation*}
In this picture, the functorial action of the Weil functor $T _ { A }$ on mappings between the $\mathbf{R} ^ { m }$ (cf. Weil algebra) extends to all smooth manifolds and smooth mappings
\begin{equation*} T _ { A } M = \operatorname { Hom } ( C ^ { \infty } ( M , \mathbf{R} ) , A ), \end{equation*}
\begin{equation*} T _ { A } f ( \varphi ) ( g ) = \varphi ( g \circ f ), \end{equation*}
where $\varphi \in \operatorname{Hom}( C ^ { \infty } ( M , \mathbf{R} ) , A )$, $f : M \rightarrow M ^ { \prime }$, $g : M ^ { \prime } \rightarrow \mathbf{R}$. At the same time, if $\varphi _ { i } : U _ { i } \subset \mathbf{R} ^ { m } \rightarrow M$ are local charts defining the smooth structure on $M$, then the functorial behaviour of $T _ { A }$ allows one to glue together the trivial bundles $T _ { A } U _ { i } = U _ { i } \times N ^ { m } \subset T _ { A } \mathbf{R} ^ { m }$ along the cocycle of the chart transitions, and this introduces the structure of the locally trivial fibre bundle on $T _ { A } M$. Altogether, one obtains a functor $T _ { A } : \mathcal{M} f \rightarrow \mathcal{M} f$ on the category of smooth manifolds and mappings, the so-called Weil bundle. This construction was first presented by A. Weil, [a11], under the name spaces of infinitely near points. The Weil bundles are particular examples of the bundle functors on the category $\mathcal{M} f$ in the sense of [a3] and their restrictions to manifolds of some fixed dimension $m$, and locally invertible mappings provide specific examples of the natural bundles of A. Nijenhuis, [a10].
Another global construction of the Weil bundles on all manifolds $M$ is due to A. Morimoto [a9], see also [a3], 35.15. Let $A$ be a Weil algebra and let $\mathcal{A}$ be the corresponding ideal of finite codimension in the algebra of germs of functions at the origin in ${\bf R} ^ { n }$. Two mappings $f , g : \mathbf{R} ^ { n } \rightarrow M$ with $f ( 0 ) = g ( 0 ) = x \in M$ are said to be $\mathcal{A}$-equivalent if $h \circ f - h \circ g \in \mathcal{A}$ for all germs $h$ of functions at $x \in M$. The equivalence classes are called $A$-velocities on $M$. Each such class $[ f ]$ determines an algebra homomorphism $h \mapsto [ h \circ f ] \in C ^ { \infty } ( {\bf R }^ { n } , {\bf R} ) /{\cal A}$ on smooth functions on $M$. Thus, one obtain the Weil bundles $T _ { A }$ again and the action of $T _ { A }$ is defined by composition in this picture. Clearly, this construction generalizes Ehresmann's $( n , r )$-velocities, i.e. the jet bundles $J ^ { r_0 } ( \mathbf{R} ^ { n } , M )$ (cf. [a2] and Jet). See Weil algebra for the corresponding Weil algebras $\mathcal{D} _ { n } ^ { r }$. The $( 1,1 )$-velocities provide the standard tangent vectors (cf. also Tangent vector) as $1$-jets of smooth curves (compare with the above definition via homomorphisms, which treats them as derivations on functions).
The construction of the Weil bundles is also functorial in the Weil algebra $A$. Moreover, the natural transformations $\eta : T _ { A } \rightarrow T _ { B }$ between two such functors are in bijective correspondence with the algebra homomorphisms $A \rightarrow B$. The smooth mappings  are simply given by composition of the homomorphism $A \rightarrow B$ with the algebra homomorphisms $\varphi \in T _ { A } M$. In particular, the bundle projections $T _ { A } M \rightarrow M$ correspond to the unique algebra homomorphism $A \rightarrow \mathbf{R}$.
are simply given by composition of the homomorphism $A \rightarrow B$ with the algebra homomorphisms $\varphi \in T _ { A } M$. In particular, the bundle projections $T _ { A } M \rightarrow M$ correspond to the unique algebra homomorphism $A \rightarrow \mathbf{R}$.
The Weil bundles have many striking categorical properties. First of all, they preserve products (i.e. $T _ { A } ( M \times M ^ { \prime } )$ is canonically isomorphic to $T _ { A } M \times T _ { A } M ^ { \prime }$). In particular, $T _ { A }$ is completely determined by its value on $\mathbf{R}$, which is the Weil algebra $A$ itself. Even its algebra structure is reconstructed by the evaluation of $T _ { A }$ on the addition and multiplication on $\mathbf{R}$. As a consequence, one can also see that the composite of two Weil bundles, $T _ { B } \circ T _ { A }$, is naturally equivalent to $T _ { B \otimes A}$. Since there is a canonical flip isomorphism $B \otimes A \rightarrow A \otimes B$, there is a corresponding natural equivalence $T _ { B } \circ T _ { A } = T _ { A } \circ T _ { B }$ of the Weil bundles. The simplest example is the well-known flip in the second iterated tangent bundle $\kappa _ { M } : T T M \rightarrow T T M$.
The Weil bundles map many classes of mappings into itself, e.g. immersions, embeddings, submersions, surjective submersions, etc. As a consequence, many structures which are defined by diagrams involving products are transfered to the values canonically. In particular, the values of Weil bundles on Lie groups are again Lie groups (cf. also Lie group) and all structural mappings, like the exponential or adjoint ones, are defined simply by the functorial action. Similarly, they behave nicely on vector bundles, principal bundles, etc.
A nice geometrical impact of these properties is the possibility of a unified approach to geometrical constructions and classification results for geometrical objects on the bundles $T _ { A } M$. Particular attention has been paid to liftings of geometrical objects, like vector fields and connections, from the underlying manifolds $M$ to the bundles $T _ { A } M$, see e.g. [a9], [a6], [a3]. An archetypical example is the natural lift of vector fields $\xi $ on $M$ to $T _ { A } M$: For all natural bundles $F$ there is a so-called flow prolongation of vector fields $\xi $ on $M$ to vector fields $F \xi$ on $F M$, whose flows are given by evaluation of the functor $F$ on the flows of $\xi $. For each Weil bundle $T _ { A }$, these flow prolongations ${\cal T} _ { A } \xi$ are given by the formula
\begin{equation*} {\cal T} _ { A } \xi = \kappa _ { M } \circ T _ { A } \xi, \end{equation*}
\begin{equation*} T _ { A } M \rightarrow T _ { A } T M \rightarrow T T _ { A } M. \end{equation*}
All natural operators of this type are then given by composition of this operator with the natural transformations $T T _ { A } \rightarrow T T _ { A }$. The latter transformations are parametrized by elements $a \in A$ and $D \in \operatorname { Der } A$, see [a6] or [a3], Section 42, for details. Many concepts and ideas of synthetic differential geometry, cf. [a5], can be recovered within such a framework.
Surprisingly, much of the structure of tangent bundles generalizes to all Weil bundles. In particular, the sections of $T _ { A } M$, $A = \mathbf{R} \cdot1 \oplus N$, are exactly the $\mathbf{R}$-linear mappings $\xi : C ^ { \infty } ( M , \mathbf{R} ) \rightarrow C ^ { \infty } ( M , N )$ satisfying the expansion property
\begin{equation*} \xi ( f . g ) = \xi ( f ) g + f . \xi ( g ) + \xi ( f ) . \xi ( g ), \end{equation*}
which generalizes the representation of vector fields as derivations on smooth functions. There is a canonical group structure on the space of all sections of $T _ { A } M$, with associated Lie algebra and exponential mapping, see [a4] or [a3], Sect. 37. Of course, the latter structures are trivial in the case of tangent bundles.
For each product-preserving functor $F : \mathcal{M} f \rightarrow \mathcal{M} f$, $F \mathbf{R}$ is a formally real finite-dimensional commutative unital algebra; thus, a finite sum of Weil algebras is not trivial. Surprisingly enough, $F$ itself is, up to some subtle topological and combinatorial phenomena, the product of the corresponding Weil bundles. Moreover, if one additionally assumes that $F$ restricts to a natural bundle in each dimension, then $F$ is of the form $T _ { A }$ with $A = F \mathbf{R}$. These results were proved in [a1], [a7], and most completely in [a4], see also [a3], Sect. 36. Note also that if $F : \mathcal{M} f \rightarrow \mathcal{M} f$ is a bundle functor on manifolds satisfying $\operatorname { dim }( F \mathbf{R} ^ { m } ) = m \operatorname { dim } ( F \mathbf{R} )$ for all $m = 0,1 , \ldots$, then $F \mathbf{R}$ is a Weil algebra and $F$ is naturally equivalent to $T _ { F \mathbf{R} }$, see [a3], Sect. 38.
The theory of product-preserving functors and Weil bundles has been extended to the infinite-dimensional manifolds modelled over convenient vector spaces, see [a8], Sect. 31.
References
| [a1] | D.J. Eck, "Product-preserving functors on smooth manifolds" J. Pure Appl. Algebra , 42 (1986) pp. 133–140 |
| [a2] | Ch. Ehresmann, "Les prolongements d'une variété différentiable. I. Calcul des jets, prolongement principal. II. L'espace des jets d'ordre $r$ de $V _ { n }$ dans $V _ { m }$. III. Transitivité des prolongements" C.R. Acad. Sci. Paris , 233 (1951) pp. 598–600; 777–779; 1081–1083 |
| [a3] | I. Kolář, P.W. Michor, J. Slovák, "Natural operations in differential geometry" , Springer (1993) |
| [a4] | G. Kainz, P.W. Michor, "Natural transformations in differential geometry" Czech. Math. J. , 37 : 112 (1987) pp. 584–607 |
| [a5] | A. Kock, "Synthetic differential geometry" , Lecture Notes , 51 , London Math. Soc. (1981) |
| [a6] | I. Kolář, "On the natural operators on vector fields" Ann. Global Anal. Geom. , 6 (1988) pp. 109–117 |
| [a7] | O.O. Luciano, "Categories of multiplicative functors and Weil's infinitely near points" Nagoya Math. J. , 109 (1988) pp. 69–89 |
| [a8] | P.W. Michor, A. Kriegl, "The convenient setting of global analysis" , Math. Surveys Monogr. , 53 , Amer. Math. Soc. (1997) |
| [a9] | A. Morimoto, "Prolongation of connections to bundles of infinitely near points" J. Diff. Geom. , 11 (1976) pp. 479–498 |
| [a10] | A. Nijenhuis, "Natural bundles and their general properties. Geometric objects revisited" , Diff. Geometry, in Honor of Kentaro Yano (1972) pp. 317–334 |
| [a11] | A. Weil, "Théorie des points proches sur les variétés différentiables" Colloq. Internat. Centre Nat. Rech. Sci. , 52 (1953) pp. 111–117 |
Weil bundle. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Weil_bundle&oldid=50599