|
|
| Line 1: |
Line 1: |
| − | Let <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c130/c130070/c1300701.png" /> be an irreducible algebraic plane curve of degree <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c130/c130070/c1300702.png" />, given by an equation <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c130/c130070/c1300703.png" /> where <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c130/c130070/c1300704.png" /> is an irreducible bivariate polynomial of degree <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c130/c130070/c1300705.png" /> over a ground field <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c130/c130070/c1300706.png" /> (cf. also [[Algebraic curve|Algebraic curve]]). For simplicity <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c130/c130070/c1300707.png" /> is assumed to be algebraically closed (cf. also [[Algebraically closed field|Algebraically closed field]]), although most of what is said below can be suitably generalized without that assumption. For the basic field theory involved, see [[#References|[a6]]] (or the modernized version [[#References|[a4]]]) and [[#References|[a3]]]. For much of the geometry to be discussed, see [[#References|[a5]]] and [[#References|[a8]]]; in particular, for the idea of points at infinity of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c130/c130070/c1300708.png" />, see [[#References|[a1]]]. For an interplay between the geometry and the algebra, see [[#References|[a2]]].
| + | <!--This article has been texified automatically. Since there was no Nroff source code for this article, |
| | + | the semi-automatic procedure described at https://encyclopediaofmath.org/wiki/User:Maximilian_Janisch/latexlist |
| | + | was used. |
| | + | If the TeX and formula formatting is correct, please remove this message and the {{TEX|semi-auto}} category. |
| | | | |
| − | One starts by analyzing when the curve <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c130/c130070/c1300709.png" /> can be rationally parametrized. For example, the unit circle <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c130/c130070/c13007010.png" /> has the rational parametrization
| + | Out of 266 formulas, 265 were replaced by TEX code.--> |
| | | | |
| − | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c130/c130070/c13007011.png" /></td> </tr></table>
| + | {{TEX|semi-auto}}{{TEX|partial}} |
| | + | Let $C$ be an irreducible algebraic plane curve of degree $n$, given by an equation $f ( X , Y ) = 0$ where $f$ is an irreducible bivariate polynomial of degree $n$ over a ground field $k$ (cf. also [[Algebraic curve|Algebraic curve]]). For simplicity $k$ is assumed to be algebraically closed (cf. also [[Algebraically closed field|Algebraically closed field]]), although most of what is said below can be suitably generalized without that assumption. For the basic field theory involved, see [[#References|[a6]]] (or the modernized version [[#References|[a4]]]) and [[#References|[a3]]]. For much of the geometry to be discussed, see [[#References|[a5]]] and [[#References|[a8]]]; in particular, for the idea of points at infinity of $C$, see [[#References|[a1]]]. For an interplay between the geometry and the algebra, see [[#References|[a2]]]. |
| | | | |
| − | Likewise, the cuspidal cubic <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c130/c130070/c13007012.png" /> has the rational parametrization <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c130/c130070/c13007013.png" /> and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c130/c130070/c13007014.png" />. However, the non-singular cubic <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c130/c130070/c13007015.png" /> does not have any rational parametrization. To obtain the parametrization of the circle, one cuts it by a line of slope <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c130/c130070/c13007016.png" /> through the point <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c130/c130070/c13007017.png" /> and notes that it meets the circle in the variable point
| + | One starts by analyzing when the curve $C$ can be rationally parametrized. For example, the unit circle $X ^ { 2 } + Y ^ { 2 } = 1$ has the rational parametrization |
| | | | |
| − | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c130/c130070/c13007018.png" /></td> </tr></table>
| + | \begin{equation*} X = \frac { 1 - t ^ { 2 } } { 1 + t ^ { 2 } } , Y = \frac { 2 t } { 1 + t ^ { 2 } }. \end{equation*} |
| | | | |
| − | For the cuspidal cubic one takes a line through the cusp <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c130/c130070/c13007019.png" /> and notes that it meets the cubic in the variable point <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c130/c130070/c13007020.png" />. This works because a line meets a circle in <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c130/c130070/c13007021.png" /> points, and it meets a cubic in <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c130/c130070/c13007022.png" /> points. In case of a cuspidal cubic two intersections are absorbed in the cusp. In case of a non-singular cubic there is no such point for the absorption. Generalizing this one can show that the curve <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c130/c130070/c13007023.png" /> cannot have more than <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c130/c130070/c13007024.png" /> double points and if it does have that many, then it can be parametrized rationally. To this end one first notes that a bivariate polynomial of degree <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c130/c130070/c13007025.png" /> has
| + | Likewise, the cuspidal cubic $Y ^ { 2 } = X ^ { 3 }$ has the rational parametrization $X = t ^ { 2 }$ and $Y = t ^ { 3 }$. However, the non-singular cubic $Y ^ { 2 } = X ^ { 3 } - 1$ does not have any rational parametrization. To obtain the parametrization of the circle, one cuts it by a line of slope $t$ through the point $( - 1,0 )$ and notes that it meets the circle in the variable point |
| | | | |
| − | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c130/c130070/c13007026.png" /></td> </tr></table>
| + | \begin{equation*} \left( \frac { 1 - t ^ { 2 } } { 1 + t ^ { 2 } } , \frac { 2 t } { 1 + t ^ { 2 } } \right). \end{equation*} |
| | | | |
| − | coefficients and hence the dimension of the system <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c130/c130070/c13007027.png" /> of curves of degree <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c130/c130070/c13007028.png" /> passing through <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c130/c130070/c13007029.png" /> double points of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c130/c130070/c13007030.png" /> is <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c130/c130070/c13007031.png" />. Next, by the [[Bezout theorem|Bezout theorem]] (which is the oldest theorem in [[Algebraic geometry|algebraic geometry]]), a curve of degree <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c130/c130070/c13007032.png" /> and a curve of degree <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c130/c130070/c13007033.png" />, having no common component, meet in <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c130/c130070/c13007034.png" /> points, counted properly. In the proper counting a double point of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c130/c130070/c13007035.png" /> should be counted twice. Thus, the number of free points in which <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c130/c130070/c13007036.png" /> meets a curve <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c130/c130070/c13007037.png" /> of degree <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c130/c130070/c13007038.png" /> passing through the <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c130/c130070/c13007039.png" /> double points of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c130/c130070/c13007040.png" /> is <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c130/c130070/c13007041.png" />. Since <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c130/c130070/c13007042.png" /> is also the dimension of the system <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c130/c130070/c13007043.png" />, the members of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c130/c130070/c13007044.png" /> which pass through <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c130/c130070/c13007045.png" /> fixed simple points of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c130/c130070/c13007046.png" /> form a pencil, i.e., a one-parameter family <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c130/c130070/c13007047.png" />, a variable member of which meets <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c130/c130070/c13007048.png" /> in one variable point whose coordinates are single-valued, and hence rational, functions of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c130/c130070/c13007049.png" />. If <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c130/c130070/c13007050.png" /> had an extra double point, then one can take a value <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c130/c130070/c13007051.png" /> of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c130/c130070/c13007052.png" /> so that <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c130/c130070/c13007053.png" /> goes through it and this would make the properly counted intersections of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c130/c130070/c13007054.png" /> and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c130/c130070/c13007055.png" /> to be <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c130/c130070/c13007056.png" />, contradicting the Bezout theorem because <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c130/c130070/c13007057.png" /> is irreducible and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c130/c130070/c13007058.png" /> has smaller degree.
| + | For the cuspidal cubic one takes a line through the cusp $( 0,0 )$ and notes that it meets the cubic in the variable point $( t ^ { 2 } , t ^ { 3 } )$. This works because a line meets a circle in $2$ points, and it meets a cubic in $3$ points. In case of a cuspidal cubic two intersections are absorbed in the cusp. In case of a non-singular cubic there is no such point for the absorption. Generalizing this one can show that the curve $C$ cannot have more than $( n - 1 ) ( n - 2 ) / 2$ double points and if it does have that many, then it can be parametrized rationally. To this end one first notes that a bivariate polynomial of degree $m$ has |
| | | | |
| − | Provisionally defining the genus <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c130/c130070/c13007059.png" /> of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c130/c130070/c13007060.png" /> (cf. also [[Genus of a curve|Genus of a curve]]) by
| + | \begin{equation*} \left( \begin{array} { c } { m + 2 } \\ { 2 } \end{array} \right) = \frac { ( m + 2 ) ( m + 1 ) } { 2 } \end{equation*} |
| | | | |
| − | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c130/c130070/c13007061.png" /></td> </tr></table>
| + | coefficients and hence the dimension of the system $S$ of curves of degree $n - 2$ passing through $( n - 1 ) ( n - 2 ) / 2$ double points of $C$ is $n ( n - 1 ) / 2 - 1 - ( n - 1 ) ( n - 2 ) / 2 = n - 2$. Next, by the [[Bezout theorem|Bezout theorem]] (which is the oldest theorem in [[Algebraic geometry|algebraic geometry]]), a curve of degree $n$ and a curve of degree $m$, having no common component, meet in <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c130/c130070/c13007034.png"/> points, counted properly. In the proper counting a double point of $C$ should be counted twice. Thus, the number of free points in which $C$ meets a curve $D$ of degree $n - 2$ passing through the $( n - 1 ) ( n - 2 ) / 2$ double points of $C$ is $n ( n - 2 ) - ( n - 1 ) ( n - 2 ) = n - 2$. Since $n - 2$ is also the dimension of the system $S$, the members of $S$ which pass through $n - 3$ fixed simple points of $C$ form a pencil, i.e., a one-parameter family $D _ { t }$, a variable member of which meets $C$ in one variable point whose coordinates are single-valued, and hence rational, functions of $t$. If $C$ had an extra double point, then one can take a value $t_0$ of $t$ so that $D _ { t _ { 0 } }$ goes through it and this would make the properly counted intersections of $C$ and $D _ { t _ { 0 } }$ to be $> n ( n - 2 )$, contradicting the Bezout theorem because $C$ is irreducible and $D _ { t _ { 0 } }$ has smaller degree. |
| | | | |
| − | one always has <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c130/c130070/c13007062.png" />, and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c130/c130070/c13007063.png" /> is rational, i.e., has a rational parametrization. To make the reverse implication <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c130/c130070/c13007064.png" /> also true, one must learn to count the double points properly. To begin with, one must include singularities of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c130/c130070/c13007065.png" /> at infinity. Next, by looking at the curve <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c130/c130070/c13007066.png" />, where <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c130/c130070/c13007067.png" /> with <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c130/c130070/c13007068.png" />, which is obviously rational and has a <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c130/c130070/c13007069.png" />-fold point at the origin and an <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c130/c130070/c13007070.png" />-fold point at infinity as its only singularities, one decides to count a <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c130/c130070/c13007071.png" />-fold point as <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c130/c130070/c13007072.png" /> double points. Before discussing infinitely near singularities, one notes that the degree <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c130/c130070/c13007073.png" /> of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c130/c130070/c13007074.png" /> can be geometrically characterized as the number of points in which a general line meets it.
| + | Provisionally defining the genus $g$ of $C$ (cf. also [[Genus of a curve|Genus of a curve]]) by |
| | | | |
| − | Likewise, the multiplicity <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c130/c130070/c13007075.png" /> of a point <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c130/c130070/c13007076.png" /> of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c130/c130070/c13007077.png" /> can be characterized geometrically by saying that <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c130/c130070/c13007078.png" /> is equal to the number of points in which a generic line through <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c130/c130070/c13007079.png" /> meets <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c130/c130070/c13007080.png" /> outside <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c130/c130070/c13007081.png" />; <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c130/c130070/c13007082.png" /> is a simple or singular point of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c130/c130070/c13007083.png" /> according as <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c130/c130070/c13007084.png" /> or <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c130/c130070/c13007085.png" />. Algebraically, by translating the coordinates one may assume <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c130/c130070/c13007086.png" /> to be the origin <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c130/c130070/c13007087.png" />, and then <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c130/c130070/c13007088.png" /> is the order of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c130/c130070/c13007089.png" />, i.e., <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c130/c130070/c13007090.png" /> has terms of degree <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c130/c130070/c13007091.png" /> but none of degree <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c130/c130070/c13007092.png" />. By making the quadratic transformation <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c130/c130070/c13007093.png" /> and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c130/c130070/c13007094.png" /> one gets <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c130/c130070/c13007095.png" />, where <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c130/c130070/c13007096.png" />: <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c130/c130070/c13007097.png" /> is the proper transform of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c130/c130070/c13007098.png" />. The exceptional line <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c130/c130070/c13007099.png" /> meets <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c130/c130070/c130070100.png" /> in points <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c130/c130070/c130070101.png" /> whose multiplicities <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c130/c130070/c130070102.png" /> add up to <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c130/c130070/c130070103.png" />. These are the points of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c130/c130070/c130070104.png" /> in the first neighbourhood of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c130/c130070/c130070105.png" />. Points in the first neighbourhoods of these points are the points of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c130/c130070/c130070106.png" /> in the second neighbourhood of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c130/c130070/c130070107.png" />, and so on. It is easily seen that all points in a high enough neighbourhood of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c130/c130070/c130070108.png" /> are simple. Now <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c130/c130070/c130070109.png" /> is counted as <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c130/c130070/c130070110.png" /> double points, where
| + | \begin{equation*} g = \frac { ( n - 1 ) ( n - 2 ) } { 2 } -\#\text{double points}, \end{equation*} |
| | | | |
| − | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c130/c130070/c130070111.png" /></td> </tr></table>
| + | one always has $g \geq 0$, and $g = 0 \Rightarrow C$ is rational, i.e., has a rational parametrization. To make the reverse implication $\Leftarrow $ also true, one must learn to count the double points properly. To begin with, one must include singularities of $C$ at infinity. Next, by looking at the curve $Y ^ { e } = X ^ { d }$, where $e > d$ with $\operatorname { gcd } ( e , d ) = 1$, which is obviously rational and has a $d$-fold point at the origin and an $( e - d )$-fold point at infinity as its only singularities, one decides to count a $d$-fold point as $d ( d - 1 ) / 2$ double points. Before discussing infinitely near singularities, one notes that the degree $n$ of $C$ can be geometrically characterized as the number of points in which a general line meets it. |
| | | | |
| − | with the summation extended over all points <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c130/c130070/c130070112.png" /> in the various neighbourhoods of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c130/c130070/c130070113.png" />, including <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c130/c130070/c130070114.png" />; here <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c130/c130070/c130070115.png" /> is the multiplicity of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c130/c130070/c130070116.png" />; clearly: <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c130/c130070/c130070117.png" /> <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c130/c130070/c130070118.png" /> <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c130/c130070/c130070119.png" /> is a simple point of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c130/c130070/c130070120.png" />. One arrives at the exact genus formula
| + | Likewise, the multiplicity $d$ of a point $P$ of $C$ can be characterized geometrically by saying that $n - d$ is equal to the number of points in which a generic line through $P$ meets $C$ outside $P$; $P$ is a simple or singular point of $C$ according as $d = 1$ or $d > 1$. Algebraically, by translating the coordinates one may assume $P$ to be the origin $( 0,0 )$, and then $d$ is the order of $f$, i.e., $f$ has terms of degree $d$ but none of degree $< d$. By making the quadratic transformation $X = X ^ { \prime }$ and $Y = X ^ { \prime } Y ^ { \prime }$ one gets $f ( X ^ { \prime } , X ^ { \prime } Y ^ { \prime } ) = X ^ { \prime d } f ^ { \prime } ( X ^ { \prime } , Y ^ { \prime } )$, where $C ^ { \prime }$: $f ^ { \prime } ( X ^ { \prime } , Y ^ { \prime } ) = 0$ is the proper transform of $C$. The exceptional line $X ^ { \prime } = 0$ meets $C ^ { \prime }$ in points $P _ { 1 } , \ldots , P _ { h }$ whose multiplicities $d _ { 1 } , \ldots , d _ { h }$ add up to $\leq d$. These are the points of $C$ in the first neighbourhood of $P$. Points in the first neighbourhoods of these points are the points of $C$ in the second neighbourhood of $P$, and so on. It is easily seen that all points in a high enough neighbourhood of $P$ are simple. Now $P$ is counted as $\delta ( P )$ double points, where |
| | | | |
| − | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c130/c130070/c130070121.png" /></td> </tr></table>
| + | \begin{equation*} \delta ( P ) = \sum \frac { d ( Q ) ( d ( Q ) - 1 ) } { 2 } \end{equation*} |
| | | | |
| − | with summation over all points <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c130/c130070/c130070122.png" /> of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c130/c130070/c130070123.png" />. One always has <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c130/c130070/c130070124.png" />; and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c130/c130070/c130070125.png" /> is rational. | + | with the summation extended over all points $Q$ in the various neighbourhoods of $P$, including $P$; here $d ( Q )$ is the multiplicity of $Q$; clearly: $\delta ( P ) = 0$ $\Leftrightarrow$ $P$ is a simple point of $C$. One arrives at the exact genus formula |
| | | | |
| − | It turns out that <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c130/c130070/c130070126.png" /> is a birational invariant of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c130/c130070/c130070127.png" />, i.e., it remains unchanged when <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c130/c130070/c130070128.png" /> undergoes a birational transformation (cf. also [[Birational morphism|Birational morphism]]). The residue class ring of the polynomial ring <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c130/c130070/c130070129.png" /> modulo the ideal generated by <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c130/c130070/c130070130.png" /> is the affine coordinate ring of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c130/c130070/c130070131.png" /> and is denoted by <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c130/c130070/c130070132.png" />. Note that <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c130/c130070/c130070133.png" /> where <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c130/c130070/c130070134.png" />, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c130/c130070/c130070135.png" /> are the images of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c130/c130070/c130070136.png" />, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c130/c130070/c130070137.png" /> in <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c130/c130070/c130070138.png" />. The quotient field <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c130/c130070/c130070139.png" /> of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c130/c130070/c130070140.png" /> is the function field of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c130/c130070/c130070141.png" />. A birational correspondence between curves <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c130/c130070/c130070142.png" /> and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c130/c130070/c130070143.png" /> is an almost one-to-one correspondence; it is given by a <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c130/c130070/c130070144.png" />-isomorphism between <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c130/c130070/c130070145.png" /> and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c130/c130070/c130070146.png" />. So one should be able to define <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c130/c130070/c130070147.png" /> directly in terms of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c130/c130070/c130070148.png" />. Following C.G.J. Jacobi one takes any differential of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c130/c130070/c130070149.png" /> (cf. also [[Differential field|Differential field]]), i.e., an expression of type <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c130/c130070/c130070150.png" /> with <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c130/c130070/c130070151.png" />, and shows that if the differential is not zero, then the number of its zeros minus the number of its poles equals <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c130/c130070/c130070152.png" />. Having brought the point <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c130/c130070/c130070153.png" /> of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c130/c130070/c130070154.png" /> to the origin, its local ring <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c130/c130070/c130070155.png" /> is defined to be the subring of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c130/c130070/c130070156.png" /> consisting of all quotients <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c130/c130070/c130070157.png" /> where <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c130/c130070/c130070158.png" />, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c130/c130070/c130070159.png" /> are polynomials with <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c130/c130070/c130070160.png" /> (cf. also [[Local ring|Local ring]]); its unique [[Maximal ideal|maximal ideal]] <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c130/c130070/c130070161.png" /> consists of the above quotients with <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c130/c130070/c130070162.png" />. Let <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c130/c130070/c130070163.png" /> be the conductor of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c130/c130070/c130070164.png" />, i.e., the largest ideal in <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c130/c130070/c130070165.png" /> which remains an ideal in the integral closure <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c130/c130070/c130070166.png" /> of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c130/c130070/c130070167.png" /> in <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c130/c130070/c130070168.png" />. It can be shown that <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c130/c130070/c130070169.png" /> is the length of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c130/c130070/c130070170.png" /> in <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c130/c130070/c130070171.png" />, i.e., the maximal length of strictly increasing chains of ideals <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c130/c130070/c130070172.png" /> in <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c130/c130070/c130070173.png" />; moreover, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c130/c130070/c130070174.png" /> is the length of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c130/c130070/c130070175.png" /> in <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c130/c130070/c130070176.png" />, which is a ubiquitous result having two dozen proofs in the literature. The ring <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c130/c130070/c130070177.png" /> has a finite number of maximal ideals and localizing <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c130/c130070/c130070178.png" /> at them gives discrete valuation rings; as <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c130/c130070/c130070179.png" /> varies over all points of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c130/c130070/c130070180.png" />, including those at infinity, these discrete valuation rings vary over the [[Riemann surface|Riemann surface]] <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c130/c130070/c130070181.png" /> of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c130/c130070/c130070182.png" />, i.e., the set of all discrete valuation rings whose quotient field is <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c130/c130070/c130070183.png" /> and which contain <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c130/c130070/c130070184.png" />. Let <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c130/c130070/c130070185.png" /> denote the localizations of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c130/c130070/c130070186.png" /> at the various maximal ideals in <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c130/c130070/c130070187.png" /> (cf. also [[Localization in a commutative algebra|Localization in a commutative algebra]]); one calls <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c130/c130070/c130070188.png" /> the centre on <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c130/c130070/c130070189.png" /> of the members of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c130/c130070/c130070190.png" />; note that <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c130/c130070/c130070191.png" /> <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c130/c130070/c130070192.png" /> <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c130/c130070/c130070193.png" /> is a simple point of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c130/c130070/c130070194.png" />, and hence for all except a finite number of points of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c130/c130070/c130070195.png" />, the set <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c130/c130070/c130070196.png" /> has exactly one member. For any <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c130/c130070/c130070197.png" /> and non-zero <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c130/c130070/c130070198.png" /> one puts
| + | \begin{equation*} g = \frac { ( n - 1 ) ( n - 2 ) } { 2 } - \sum \delta ( P ), \end{equation*} |
| | | | |
| − | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c130/c130070/c130070199.png" /></td> </tr></table>
| + | with summation over all points $P$ of $C$. One always has $g \geq 0$; and $g = 0 \Leftrightarrow C$ is rational. |
| | | | |
| − | with <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c130/c130070/c130070200.png" /> and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c130/c130070/c130070201.png" />; take <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c130/c130070/c130070202.png" /> with <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c130/c130070/c130070203.png" /> and define
| + | It turns out that $g$ is a birational invariant of $C$, i.e., it remains unchanged when $C$ undergoes a birational transformation (cf. also [[Birational morphism|Birational morphism]]). The residue class ring of the polynomial ring $k [ X , Y ]$ modulo the ideal generated by $f ( X , Y )$ is the affine coordinate ring of $C$ and is denoted by $k [ C ]$. Note that $k [ C ] = k [ x , y ]$ where $x$, $y$ are the images of $X$, $Y$ in $k [ C ]$. The quotient field $k ( C ) = k ( x , y )$ of $k [ C ]$ is the function field of $C$. A birational correspondence between curves $C$ and $C ^ { * }$ is an almost one-to-one correspondence; it is given by a $k$-isomorphism between $k ( C )$ and $k ( C ^ { * } )$. So one should be able to define $g$ directly in terms of $k ( C )$. Following C.G.J. Jacobi one takes any differential of $k ( C )$ (cf. also [[Differential field|Differential field]]), i.e., an expression of type $ud v$ with $u , v \in k ( C )$, and shows that if the differential is not zero, then the number of its zeros minus the number of its poles equals $2 g - 2$. Having brought the point $P$ of $C$ to the origin, its local ring $R ( P )$ is defined to be the subring of $k ( C )$ consisting of all quotients $r ( x , y ) / s ( x , y )$ where $r ( X , Y )$, $s ( X , Y )$ are polynomials with $s ( 0,0 ) \neq 0$ (cf. also [[Local ring|Local ring]]); its unique [[Maximal ideal|maximal ideal]] $M ( R ( P ) )$ consists of the above quotients with $r ( 0,0 ) = 0$. Let ${\frak C} ( P )$ be the conductor of $R ( P )$, i.e., the largest ideal in $R ( P )$ which remains an ideal in the integral closure $R ^ { \prime } ( P )$ of $R ( P )$ in $k ( C )$. It can be shown that $\delta ( P )$ is the length of ${\frak C} ( P )$ in $R ( P )$, i.e., the maximal length of strictly increasing chains of ideals $\mathfrak { C } ( P ) = I _ { 0 } \subset \ldots \subset I _ { \delta } = R ( P )$ in $R ( P )$; moreover, $2 \delta ( P )$ is the length of ${\frak C} ( P )$ in $R ^ { \prime } ( P )$, which is a ubiquitous result having two dozen proofs in the literature. The ring $R ^ { \prime } ( P )$ has a finite number of maximal ideals and localizing $R ^ { \prime } ( P )$ at them gives discrete valuation rings; as $P$ varies over all points of $C$, including those at infinity, these discrete valuation rings vary over the [[Riemann surface|Riemann surface]] $\Re ( C )$ of $C$, i.e., the set of all discrete valuation rings whose quotient field is $k ( C )$ and which contain $k$. Let $\mathfrak { R } ( C , P )$ denote the localizations of $R ^ { \prime } ( P )$ at the various maximal ideals in $R ^ { \prime } ( P )$ (cf. also [[Localization in a commutative algebra|Localization in a commutative algebra]]); one calls $P$ the centre on $C$ of the members of $\mathfrak { R } ( C , P )$; note that $R ^ { \prime } ( P ) = R ( P )$ $\Leftrightarrow$ $P$ is a simple point of $C$, and hence for all except a finite number of points of $C$, the set $\mathfrak { R } ( C , P )$ has exactly one member. For any $T \in \Re ( C )$ and non-zero $r , s \in k ( C )$ one puts |
| | | | |
| − | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c130/c130070/c130070204.png" /></td> </tr></table>
| + | \begin{equation*} \operatorname { ord } _ { T } ( r / s ) = \lambda - \mu, \end{equation*} |
| | | | |
| − | one calls <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c130/c130070/c130070205.png" /> a uniformizing parameter of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c130/c130070/c130070206.png" />. Now the number of zeros minus number of poles of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c130/c130070/c130070207.png" /> equals <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c130/c130070/c130070208.png" /> taken over all <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c130/c130070/c130070209.png" /> in <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c130/c130070/c130070210.png" />. For any point <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c130/c130070/c130070211.png" /> of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c130/c130070/c130070212.png" />, not at infinity, one has Dedekind's formula
| + | with $r T = M ( T ) ^ { \lambda }$ and $s T = M ( T ) ^ { \mu }$; take $\tau \in T$ with $\tau T = M ( T )$ and define |
| | | | |
| − | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c130/c130070/c130070213.png" /></td> </tr></table>
| + | \begin{equation*} \operatorname { ord } _ { T } ( u d v ) = \operatorname { ord } _ { T } ( u d v / d \tau ); \end{equation*} |
| | | | |
| − | where <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c130/c130070/c130070214.png" /> is the different ideal in <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c130/c130070/c130070215.png" /> defined by saying that <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c130/c130070/c130070216.png" /> with <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c130/c130070/c130070217.png" /> for every <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c130/c130070/c130070218.png" />.
| + | one calls $\tau$ a uniformizing parameter of $T$. Now the number of zeros minus number of poles of $ud v$ equals $\sum \text { ord }_{ T } ( u d v )$ taken over all $T$ in $\Re ( C )$. For any point $P$ of $C$, not at infinity, one has Dedekind's formula |
| | | | |
| − | For <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c130/c130070/c130070219.png" />, let <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c130/c130070/c130070220.png" /> be an irreducible algebraic plane curve such that <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c130/c130070/c130070221.png" /> is a finite separable algebraic field extension of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c130/c130070/c130070222.png" /> of field degree <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c130/c130070/c130070223.png" /> (cf. also [[Extension of a field|Extension of a field]]; [[Separable extension|Separable extension]]). This defines a <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c130/c130070/c130070224.png" /> correspondence between <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c130/c130070/c130070225.png" /> and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c130/c130070/c130070226.png" />, and hence between <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c130/c130070/c130070227.png" /> and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c130/c130070/c130070228.png" />; namely, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c130/c130070/c130070229.png" /> and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c130/c130070/c130070230.png" /> correspond if and only if for some <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c130/c130070/c130070231.png" /> one has <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c130/c130070/c130070232.png" /> and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c130/c130070/c130070233.png" />. Let <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c130/c130070/c130070234.png" /> be the genus of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c130/c130070/c130070235.png" />, let the different <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c130/c130070/c130070236.png" /> be the integer-valued function on <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c130/c130070/c130070237.png" /> whose value at <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c130/c130070/c130070238.png" /> in <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c130/c130070/c130070239.png" /> is given by <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c130/c130070/c130070240.png" />, where <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c130/c130070/c130070241.png" /> is a uniformizing parameter of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c130/c130070/c130070242.png" />, and let <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c130/c130070/c130070243.png" /> with summation over all <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c130/c130070/c130070244.png" />. Then the Riemann–Hurwitz formula says that
| + | \begin{equation*} f _ { Y } ( x , y ) R ^ { \prime } ( P ) = \mathfrak { C } ( P ) \mathfrak { D } ( P , x ), \end{equation*} |
| | | | |
| − | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c130/c130070/c130070245.png" /></td> </tr></table>
| + | where $\mathfrak { D } ( P , x )$ is the different ideal in $R ^ { \prime } ( P )$ defined by saying that $\mathfrak { D } ( P , x ) T = M ( T ) ^ { \epsilon }$ with $\epsilon = \operatorname { ord } _ { T } ( d x / d \tau )$ for every $T \in \Re ( C , P )$. |
| | + | |
| | + | For $i = 1,2$, let $C_i$ be an irreducible algebraic plane curve such that $k ( C )$ is a finite separable algebraic field extension of $k ( C _ { i } )$ of field degree $\nu _ { i }$ (cf. also [[Extension of a field|Extension of a field]]; [[Separable extension|Separable extension]]). This defines a $( \nu _ { 1 } , \nu _ { 2 } )$ correspondence between $\mathfrak { R } ( C _ { 1 } )$ and $\mathfrak { R } ( C _ { 2 } )$, and hence between $C _ { 1 }$ and $C _ { 2 }$; namely, $T _ { 1 } \in \Re ( C _ { 1 } )$ and $T _ { 2 } \in \Re ( C _ { 2 } )$ correspond if and only if for some $T \in \Re ( C )$ one has $T \cap k ( C _ { 1 } ) = T _ { 1 }$ and $T \cap k ( C _ { 2 } ) = T _ { 2 }$. Let $g_i$ be the genus of $C_i$, let the different $\mathfrak { D } ( C , C _ { i } )$ be the integer-valued function on $\Re ( C )$ whose value at $T$ in $\Re ( C )$ is given by $\operatorname { ord } _ { T } ( d \tau _ { i } / d \tau )$, where $\tau_i$ is a uniformizing parameter of $T \cap k ( C _ { i } )$, and let $\mathfrak { D } _ { i } = \sum \mathfrak { D } ( C , C _ { i } ) ( T )$ with summation over all $T \in \Re ( C )$. Then the Riemann–Hurwitz formula says that |
| | + | |
| | + | \begin{equation*} 2 g - 2 = \nu _ { i } ( 2 g _ { i } - 2 ) + \mathfrak { D } _ { i }, \end{equation*} |
| | | | |
| | and this gives rise to the Zeuthen formula | | and this gives rise to the Zeuthen formula |
| | | | |
| − | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c130/c130070/c130070246.png" /></td> </tr></table>
| + | \begin{equation*} \nu _ { 1 } ( 2 g _ { 1 } - 2 ) + \mathfrak { D } _ { 1 } = \nu _ { 2 } ( 2 g _ { 2 } - 2 ) + \mathfrak { D } _ { 2 }. \end{equation*} |
| | | | |
| − | Now suppose there is a <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c130/c130070/c130070247.png" />-isomorphism <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c130/c130070/c130070248.png" />. Then <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c130/c130070/c130070249.png" /> is called a fixed place of the correspondence if <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c130/c130070/c130070250.png" />. The Chasles–Cayley–Brill formula says that under suitable conditions, the number of these, counted properly, equals <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c130/c130070/c130070251.png" />, where the integer <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c130/c130070/c130070252.png" /> is called the valence of the correspondence. For details see [[#References|[a7]]], pp. 189–194. | + | Now suppose there is a $k$-isomorphism $\phi : k ( C _ { 1 } ) \rightarrow k ( C _ { 2 } )$. Then $T \in \Re ( C )$ is called a fixed place of the correspondence if $T \cap k ( C _ { 2 } ) = \phi ( T \cap k ( C _ { 1 } ) )$. The Chasles–Cayley–Brill formula says that under suitable conditions, the number of these, counted properly, equals $\nu _ { 1 } + \nu _ { 2 } + 2 \gamma g$, where the integer $\gamma$ is called the valence of the correspondence. For details see [[#References|[a7]]], pp. 189–194. |
| | | | |
| − | In case <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c130/c130070/c130070253.png" /> is the field of complex numbers, to describe Riemann's approach one topologizes <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c130/c130070/c130070254.png" /> to make it into a compact orientable two-dimensional real manifold, and hence into a sphere with <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c130/c130070/c130070255.png" /> handles (cf. also [[Riemann surface|Riemann surface]]). Likewise, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c130/c130070/c130070256.png" /> is made into a sphere with <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c130/c130070/c130070257.png" /> handles. Triangulate <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c130/c130070/c130070258.png" /> by including all the branch points as vertices, and lift this triangulation to a triangulation of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c130/c130070/c130070259.png" />. Let <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c130/c130070/c130070260.png" /> and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c130/c130070/c130070261.png" /> be the vertices, edges, faces of the bottom and top triangulations respectively. Then <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c130/c130070/c130070262.png" />, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c130/c130070/c130070263.png" />, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c130/c130070/c130070264.png" />, and hence by the Euler–Poincaré theorem one obtains | + | In case $k$ is the field of complex numbers, to describe Riemann's approach one topologizes $\Re ( C )$ to make it into a compact orientable two-dimensional real manifold, and hence into a sphere with $g$ handles (cf. also [[Riemann surface|Riemann surface]]). Likewise, $\mathfrak { R } ( C _ { 1 } )$ is made into a sphere with $g_1$ handles. Triangulate $\mathfrak { R } ( C _ { 1 } )$ by including all the branch points as vertices, and lift this triangulation to a triangulation of $\Re ( C )$. Let $( V _ { 1 } , E _ { 1 } , F _ { 1 } )$ and $( V , E , F )$ be the vertices, edges, faces of the bottom and top triangulations respectively. Then $V = \nu _ { 1 } V _ { 1 } - \mathfrak { D } _ { 1 }$, $E = \nu _ { 1 } E _ { 1 }$, $F = \nu _ { 1 } F _ { 1 }$, and hence by the Euler–Poincaré theorem one obtains |
| | | | |
| − | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c130/c130070/c130070265.png" /></td> </tr></table>
| + | \begin{equation*} 2 g - 2 = \nu _ { 1 } ( 2 g _ { 1 } - 2 ) + \mathfrak { D } _ { 1 }. \end{equation*} |
| | | | |
| − | This proves the birational invariance of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c130/c130070/c130070266.png" /> and the Riemann–Hurwitz formula. For details, see [[#References|[a2]]] and [[#References|[a4]]]. | + | This proves the birational invariance of $g$ and the Riemann–Hurwitz formula. For details, see [[#References|[a2]]] and [[#References|[a4]]]. |
| | | | |
| | ====References==== | | ====References==== |
| − | <table><TR><TD valign="top">[a1]</TD> <TD valign="top"> S.S. Abhyankar, "What is the difference between a parabola and a hyperbola" ''Math. Intelligencer'' , '''10''' (1988) pp. 36–43</TD></TR><TR><TD valign="top">[a2]</TD> <TD valign="top"> S.S. Abhyankar, "Algebraic geometry for scientists and engineers" , Amer. Math. Soc. (1990) {{MR|1075991}} {{ZBL|0709.14001}} {{ZBL|0721.14001}} </TD></TR><TR><TD valign="top">[a3]</TD> <TD valign="top"> S.S. Abhyankar, "Field extensions" G.A. Pilz (ed.) A.V. Mikhalev (ed.) , ''Handbook of the Heart of Algebra'' , Kluwer Acad. Publ. (to appear)</TD></TR><TR><TD valign="top">[a4]</TD> <TD valign="top"> C. Chevalley, "Introduction to the theory of algebraic functions of one variable" , ''Math. Surveys'' , '''6''' , Amer. Math. Soc. (1951) {{MR|0042164}} {{ZBL|0045.32301}} </TD></TR><TR><TD valign="top">[a5]</TD> <TD valign="top"> J.L. Coolidge, "A treatise on algebraic plane curves" , Clarendon Press (1931) {{MR|0120551}} {{MR|1522528}} {{ZBL|57.0820.06}} </TD></TR><TR><TD valign="top">[a6]</TD> <TD valign="top"> R. Dedekind, H. Weber, "Theorie der algebraischen Functionen einer Veränderlichen" ''Crelle J.'' , '''92''' (1882) pp. 181–290</TD></TR><TR><TD valign="top">[a7]</TD> <TD valign="top"> S. Lefschetz, "Algebraic geometry" , Princeton Univ. Press (1953)</TD></TR><TR><TD valign="top">[a8]</TD> <TD valign="top"> F. Severi, "Vorlesungen über algebraische Geometrie" , Teubner (1921) {{MR|0245574}} {{ZBL|48.0687.01}} </TD></TR></table> | + | <table><tr><td valign="top">[a1]</td> <td valign="top"> S.S. Abhyankar, "What is the difference between a parabola and a hyperbola" ''Math. Intelligencer'' , '''10''' (1988) pp. 36–43</td></tr><tr><td valign="top">[a2]</td> <td valign="top"> S.S. Abhyankar, "Algebraic geometry for scientists and engineers" , Amer. Math. Soc. (1990) {{MR|1075991}} {{ZBL|0709.14001}} {{ZBL|0721.14001}} </td></tr><tr><td valign="top">[a3]</td> <td valign="top"> S.S. Abhyankar, "Field extensions" G.A. Pilz (ed.) A.V. Mikhalev (ed.) , ''Handbook of the Heart of Algebra'' , Kluwer Acad. Publ. (to appear)</td></tr><tr><td valign="top">[a4]</td> <td valign="top"> C. Chevalley, "Introduction to the theory of algebraic functions of one variable" , ''Math. Surveys'' , '''6''' , Amer. Math. Soc. (1951) {{MR|0042164}} {{ZBL|0045.32301}} </td></tr><tr><td valign="top">[a5]</td> <td valign="top"> J.L. Coolidge, "A treatise on algebraic plane curves" , Clarendon Press (1931) {{MR|0120551}} {{MR|1522528}} {{ZBL|57.0820.06}} </td></tr><tr><td valign="top">[a6]</td> <td valign="top"> R. Dedekind, H. Weber, "Theorie der algebraischen Functionen einer Veränderlichen" ''Crelle J.'' , '''92''' (1882) pp. 181–290</td></tr><tr><td valign="top">[a7]</td> <td valign="top"> S. Lefschetz, "Algebraic geometry" , Princeton Univ. Press (1953)</td></tr><tr><td valign="top">[a8]</td> <td valign="top"> F. Severi, "Vorlesungen über algebraische Geometrie" , Teubner (1921) {{MR|0245574}} {{ZBL|48.0687.01}} </td></tr></table> |
Let $C$ be an irreducible algebraic plane curve of degree $n$, given by an equation $f ( X , Y ) = 0$ where $f$ is an irreducible bivariate polynomial of degree $n$ over a ground field $k$ (cf. also Algebraic curve). For simplicity $k$ is assumed to be algebraically closed (cf. also Algebraically closed field), although most of what is said below can be suitably generalized without that assumption. For the basic field theory involved, see [a6] (or the modernized version [a4]) and [a3]. For much of the geometry to be discussed, see [a5] and [a8]; in particular, for the idea of points at infinity of $C$, see [a1]. For an interplay between the geometry and the algebra, see [a2].
One starts by analyzing when the curve $C$ can be rationally parametrized. For example, the unit circle $X ^ { 2 } + Y ^ { 2 } = 1$ has the rational parametrization
\begin{equation*} X = \frac { 1 - t ^ { 2 } } { 1 + t ^ { 2 } } , Y = \frac { 2 t } { 1 + t ^ { 2 } }. \end{equation*}
Likewise, the cuspidal cubic $Y ^ { 2 } = X ^ { 3 }$ has the rational parametrization $X = t ^ { 2 }$ and $Y = t ^ { 3 }$. However, the non-singular cubic $Y ^ { 2 } = X ^ { 3 } - 1$ does not have any rational parametrization. To obtain the parametrization of the circle, one cuts it by a line of slope $t$ through the point $( - 1,0 )$ and notes that it meets the circle in the variable point
\begin{equation*} \left( \frac { 1 - t ^ { 2 } } { 1 + t ^ { 2 } } , \frac { 2 t } { 1 + t ^ { 2 } } \right). \end{equation*}
For the cuspidal cubic one takes a line through the cusp $( 0,0 )$ and notes that it meets the cubic in the variable point $( t ^ { 2 } , t ^ { 3 } )$. This works because a line meets a circle in $2$ points, and it meets a cubic in $3$ points. In case of a cuspidal cubic two intersections are absorbed in the cusp. In case of a non-singular cubic there is no such point for the absorption. Generalizing this one can show that the curve $C$ cannot have more than $( n - 1 ) ( n - 2 ) / 2$ double points and if it does have that many, then it can be parametrized rationally. To this end one first notes that a bivariate polynomial of degree $m$ has
\begin{equation*} \left( \begin{array} { c } { m + 2 } \\ { 2 } \end{array} \right) = \frac { ( m + 2 ) ( m + 1 ) } { 2 } \end{equation*}
coefficients and hence the dimension of the system $S$ of curves of degree $n - 2$ passing through $( n - 1 ) ( n - 2 ) / 2$ double points of $C$ is $n ( n - 1 ) / 2 - 1 - ( n - 1 ) ( n - 2 ) / 2 = n - 2$. Next, by the Bezout theorem (which is the oldest theorem in algebraic geometry), a curve of degree $n$ and a curve of degree $m$, having no common component, meet in 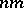 points, counted properly. In the proper counting a double point of $C$ should be counted twice. Thus, the number of free points in which $C$ meets a curve $D$ of degree $n - 2$ passing through the $( n - 1 ) ( n - 2 ) / 2$ double points of $C$ is $n ( n - 2 ) - ( n - 1 ) ( n - 2 ) = n - 2$. Since $n - 2$ is also the dimension of the system $S$, the members of $S$ which pass through $n - 3$ fixed simple points of $C$ form a pencil, i.e., a one-parameter family $D _ { t }$, a variable member of which meets $C$ in one variable point whose coordinates are single-valued, and hence rational, functions of $t$. If $C$ had an extra double point, then one can take a value $t_0$ of $t$ so that $D _ { t _ { 0 } }$ goes through it and this would make the properly counted intersections of $C$ and $D _ { t _ { 0 } }$ to be $> n ( n - 2 )$, contradicting the Bezout theorem because $C$ is irreducible and $D _ { t _ { 0 } }$ has smaller degree.
points, counted properly. In the proper counting a double point of $C$ should be counted twice. Thus, the number of free points in which $C$ meets a curve $D$ of degree $n - 2$ passing through the $( n - 1 ) ( n - 2 ) / 2$ double points of $C$ is $n ( n - 2 ) - ( n - 1 ) ( n - 2 ) = n - 2$. Since $n - 2$ is also the dimension of the system $S$, the members of $S$ which pass through $n - 3$ fixed simple points of $C$ form a pencil, i.e., a one-parameter family $D _ { t }$, a variable member of which meets $C$ in one variable point whose coordinates are single-valued, and hence rational, functions of $t$. If $C$ had an extra double point, then one can take a value $t_0$ of $t$ so that $D _ { t _ { 0 } }$ goes through it and this would make the properly counted intersections of $C$ and $D _ { t _ { 0 } }$ to be $> n ( n - 2 )$, contradicting the Bezout theorem because $C$ is irreducible and $D _ { t _ { 0 } }$ has smaller degree.
Provisionally defining the genus $g$ of $C$ (cf. also Genus of a curve) by
\begin{equation*} g = \frac { ( n - 1 ) ( n - 2 ) } { 2 } -\#\text{double points}, \end{equation*}
one always has $g \geq 0$, and $g = 0 \Rightarrow C$ is rational, i.e., has a rational parametrization. To make the reverse implication $\Leftarrow $ also true, one must learn to count the double points properly. To begin with, one must include singularities of $C$ at infinity. Next, by looking at the curve $Y ^ { e } = X ^ { d }$, where $e > d$ with $\operatorname { gcd } ( e , d ) = 1$, which is obviously rational and has a $d$-fold point at the origin and an $( e - d )$-fold point at infinity as its only singularities, one decides to count a $d$-fold point as $d ( d - 1 ) / 2$ double points. Before discussing infinitely near singularities, one notes that the degree $n$ of $C$ can be geometrically characterized as the number of points in which a general line meets it.
Likewise, the multiplicity $d$ of a point $P$ of $C$ can be characterized geometrically by saying that $n - d$ is equal to the number of points in which a generic line through $P$ meets $C$ outside $P$; $P$ is a simple or singular point of $C$ according as $d = 1$ or $d > 1$. Algebraically, by translating the coordinates one may assume $P$ to be the origin $( 0,0 )$, and then $d$ is the order of $f$, i.e., $f$ has terms of degree $d$ but none of degree $< d$. By making the quadratic transformation $X = X ^ { \prime }$ and $Y = X ^ { \prime } Y ^ { \prime }$ one gets $f ( X ^ { \prime } , X ^ { \prime } Y ^ { \prime } ) = X ^ { \prime d } f ^ { \prime } ( X ^ { \prime } , Y ^ { \prime } )$, where $C ^ { \prime }$: $f ^ { \prime } ( X ^ { \prime } , Y ^ { \prime } ) = 0$ is the proper transform of $C$. The exceptional line $X ^ { \prime } = 0$ meets $C ^ { \prime }$ in points $P _ { 1 } , \ldots , P _ { h }$ whose multiplicities $d _ { 1 } , \ldots , d _ { h }$ add up to $\leq d$. These are the points of $C$ in the first neighbourhood of $P$. Points in the first neighbourhoods of these points are the points of $C$ in the second neighbourhood of $P$, and so on. It is easily seen that all points in a high enough neighbourhood of $P$ are simple. Now $P$ is counted as $\delta ( P )$ double points, where
\begin{equation*} \delta ( P ) = \sum \frac { d ( Q ) ( d ( Q ) - 1 ) } { 2 } \end{equation*}
with the summation extended over all points $Q$ in the various neighbourhoods of $P$, including $P$; here $d ( Q )$ is the multiplicity of $Q$; clearly: $\delta ( P ) = 0$ $\Leftrightarrow$ $P$ is a simple point of $C$. One arrives at the exact genus formula
\begin{equation*} g = \frac { ( n - 1 ) ( n - 2 ) } { 2 } - \sum \delta ( P ), \end{equation*}
with summation over all points $P$ of $C$. One always has $g \geq 0$; and $g = 0 \Leftrightarrow C$ is rational.
It turns out that $g$ is a birational invariant of $C$, i.e., it remains unchanged when $C$ undergoes a birational transformation (cf. also Birational morphism). The residue class ring of the polynomial ring $k [ X , Y ]$ modulo the ideal generated by $f ( X , Y )$ is the affine coordinate ring of $C$ and is denoted by $k [ C ]$. Note that $k [ C ] = k [ x , y ]$ where $x$, $y$ are the images of $X$, $Y$ in $k [ C ]$. The quotient field $k ( C ) = k ( x , y )$ of $k [ C ]$ is the function field of $C$. A birational correspondence between curves $C$ and $C ^ { * }$ is an almost one-to-one correspondence; it is given by a $k$-isomorphism between $k ( C )$ and $k ( C ^ { * } )$. So one should be able to define $g$ directly in terms of $k ( C )$. Following C.G.J. Jacobi one takes any differential of $k ( C )$ (cf. also Differential field), i.e., an expression of type $ud v$ with $u , v \in k ( C )$, and shows that if the differential is not zero, then the number of its zeros minus the number of its poles equals $2 g - 2$. Having brought the point $P$ of $C$ to the origin, its local ring $R ( P )$ is defined to be the subring of $k ( C )$ consisting of all quotients $r ( x , y ) / s ( x , y )$ where $r ( X , Y )$, $s ( X , Y )$ are polynomials with $s ( 0,0 ) \neq 0$ (cf. also Local ring); its unique maximal ideal $M ( R ( P ) )$ consists of the above quotients with $r ( 0,0 ) = 0$. Let ${\frak C} ( P )$ be the conductor of $R ( P )$, i.e., the largest ideal in $R ( P )$ which remains an ideal in the integral closure $R ^ { \prime } ( P )$ of $R ( P )$ in $k ( C )$. It can be shown that $\delta ( P )$ is the length of ${\frak C} ( P )$ in $R ( P )$, i.e., the maximal length of strictly increasing chains of ideals $\mathfrak { C } ( P ) = I _ { 0 } \subset \ldots \subset I _ { \delta } = R ( P )$ in $R ( P )$; moreover, $2 \delta ( P )$ is the length of ${\frak C} ( P )$ in $R ^ { \prime } ( P )$, which is a ubiquitous result having two dozen proofs in the literature. The ring $R ^ { \prime } ( P )$ has a finite number of maximal ideals and localizing $R ^ { \prime } ( P )$ at them gives discrete valuation rings; as $P$ varies over all points of $C$, including those at infinity, these discrete valuation rings vary over the Riemann surface $\Re ( C )$ of $C$, i.e., the set of all discrete valuation rings whose quotient field is $k ( C )$ and which contain $k$. Let $\mathfrak { R } ( C , P )$ denote the localizations of $R ^ { \prime } ( P )$ at the various maximal ideals in $R ^ { \prime } ( P )$ (cf. also Localization in a commutative algebra); one calls $P$ the centre on $C$ of the members of $\mathfrak { R } ( C , P )$; note that $R ^ { \prime } ( P ) = R ( P )$ $\Leftrightarrow$ $P$ is a simple point of $C$, and hence for all except a finite number of points of $C$, the set $\mathfrak { R } ( C , P )$ has exactly one member. For any $T \in \Re ( C )$ and non-zero $r , s \in k ( C )$ one puts
\begin{equation*} \operatorname { ord } _ { T } ( r / s ) = \lambda - \mu, \end{equation*}
with $r T = M ( T ) ^ { \lambda }$ and $s T = M ( T ) ^ { \mu }$; take $\tau \in T$ with $\tau T = M ( T )$ and define
\begin{equation*} \operatorname { ord } _ { T } ( u d v ) = \operatorname { ord } _ { T } ( u d v / d \tau ); \end{equation*}
one calls $\tau$ a uniformizing parameter of $T$. Now the number of zeros minus number of poles of $ud v$ equals $\sum \text { ord }_{ T } ( u d v )$ taken over all $T$ in $\Re ( C )$. For any point $P$ of $C$, not at infinity, one has Dedekind's formula
\begin{equation*} f _ { Y } ( x , y ) R ^ { \prime } ( P ) = \mathfrak { C } ( P ) \mathfrak { D } ( P , x ), \end{equation*}
where $\mathfrak { D } ( P , x )$ is the different ideal in $R ^ { \prime } ( P )$ defined by saying that $\mathfrak { D } ( P , x ) T = M ( T ) ^ { \epsilon }$ with $\epsilon = \operatorname { ord } _ { T } ( d x / d \tau )$ for every $T \in \Re ( C , P )$.
For $i = 1,2$, let $C_i$ be an irreducible algebraic plane curve such that $k ( C )$ is a finite separable algebraic field extension of $k ( C _ { i } )$ of field degree $\nu _ { i }$ (cf. also Extension of a field; Separable extension). This defines a $( \nu _ { 1 } , \nu _ { 2 } )$ correspondence between $\mathfrak { R } ( C _ { 1 } )$ and $\mathfrak { R } ( C _ { 2 } )$, and hence between $C _ { 1 }$ and $C _ { 2 }$; namely, $T _ { 1 } \in \Re ( C _ { 1 } )$ and $T _ { 2 } \in \Re ( C _ { 2 } )$ correspond if and only if for some $T \in \Re ( C )$ one has $T \cap k ( C _ { 1 } ) = T _ { 1 }$ and $T \cap k ( C _ { 2 } ) = T _ { 2 }$. Let $g_i$ be the genus of $C_i$, let the different $\mathfrak { D } ( C , C _ { i } )$ be the integer-valued function on $\Re ( C )$ whose value at $T$ in $\Re ( C )$ is given by $\operatorname { ord } _ { T } ( d \tau _ { i } / d \tau )$, where $\tau_i$ is a uniformizing parameter of $T \cap k ( C _ { i } )$, and let $\mathfrak { D } _ { i } = \sum \mathfrak { D } ( C , C _ { i } ) ( T )$ with summation over all $T \in \Re ( C )$. Then the Riemann–Hurwitz formula says that
\begin{equation*} 2 g - 2 = \nu _ { i } ( 2 g _ { i } - 2 ) + \mathfrak { D } _ { i }, \end{equation*}
and this gives rise to the Zeuthen formula
\begin{equation*} \nu _ { 1 } ( 2 g _ { 1 } - 2 ) + \mathfrak { D } _ { 1 } = \nu _ { 2 } ( 2 g _ { 2 } - 2 ) + \mathfrak { D } _ { 2 }. \end{equation*}
Now suppose there is a $k$-isomorphism $\phi : k ( C _ { 1 } ) \rightarrow k ( C _ { 2 } )$. Then $T \in \Re ( C )$ is called a fixed place of the correspondence if $T \cap k ( C _ { 2 } ) = \phi ( T \cap k ( C _ { 1 } ) )$. The Chasles–Cayley–Brill formula says that under suitable conditions, the number of these, counted properly, equals $\nu _ { 1 } + \nu _ { 2 } + 2 \gamma g$, where the integer $\gamma$ is called the valence of the correspondence. For details see [a7], pp. 189–194.
In case $k$ is the field of complex numbers, to describe Riemann's approach one topologizes $\Re ( C )$ to make it into a compact orientable two-dimensional real manifold, and hence into a sphere with $g$ handles (cf. also Riemann surface). Likewise, $\mathfrak { R } ( C _ { 1 } )$ is made into a sphere with $g_1$ handles. Triangulate $\mathfrak { R } ( C _ { 1 } )$ by including all the branch points as vertices, and lift this triangulation to a triangulation of $\Re ( C )$. Let $( V _ { 1 } , E _ { 1 } , F _ { 1 } )$ and $( V , E , F )$ be the vertices, edges, faces of the bottom and top triangulations respectively. Then $V = \nu _ { 1 } V _ { 1 } - \mathfrak { D } _ { 1 }$, $E = \nu _ { 1 } E _ { 1 }$, $F = \nu _ { 1 } F _ { 1 }$, and hence by the Euler–Poincaré theorem one obtains
\begin{equation*} 2 g - 2 = \nu _ { 1 } ( 2 g _ { 1 } - 2 ) + \mathfrak { D } _ { 1 }. \end{equation*}
This proves the birational invariance of $g$ and the Riemann–Hurwitz formula. For details, see [a2] and [a4].
References
| [a1] | S.S. Abhyankar, "What is the difference between a parabola and a hyperbola" Math. Intelligencer , 10 (1988) pp. 36–43 |
| [a2] | S.S. Abhyankar, "Algebraic geometry for scientists and engineers" , Amer. Math. Soc. (1990) MR1075991 Zbl 0709.14001 Zbl 0721.14001 |
| [a3] | S.S. Abhyankar, "Field extensions" G.A. Pilz (ed.) A.V. Mikhalev (ed.) , Handbook of the Heart of Algebra , Kluwer Acad. Publ. (to appear) |
| [a4] | C. Chevalley, "Introduction to the theory of algebraic functions of one variable" , Math. Surveys , 6 , Amer. Math. Soc. (1951) MR0042164 Zbl 0045.32301 |
| [a5] | J.L. Coolidge, "A treatise on algebraic plane curves" , Clarendon Press (1931) MR0120551 MR1522528 Zbl 57.0820.06 |
| [a6] | R. Dedekind, H. Weber, "Theorie der algebraischen Functionen einer Veränderlichen" Crelle J. , 92 (1882) pp. 181–290 |
| [a7] | S. Lefschetz, "Algebraic geometry" , Princeton Univ. Press (1953) |
| [a8] | F. Severi, "Vorlesungen über algebraische Geometrie" , Teubner (1921) MR0245574 Zbl 48.0687.01 |
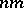 points, counted properly. In the proper counting a double point of $C$ should be counted twice. Thus, the number of free points in which $C$ meets a curve $D$ of degree $n - 2$ passing through the $( n - 1 ) ( n - 2 ) / 2$ double points of $C$ is $n ( n - 2 ) - ( n - 1 ) ( n - 2 ) = n - 2$. Since $n - 2$ is also the dimension of the system $S$, the members of $S$ which pass through $n - 3$ fixed simple points of $C$ form a pencil, i.e., a one-parameter family $D _ { t }$, a variable member of which meets $C$ in one variable point whose coordinates are single-valued, and hence rational, functions of $t$. If $C$ had an extra double point, then one can take a value $t_0$ of $t$ so that $D _ { t _ { 0 } }$ goes through it and this would make the properly counted intersections of $C$ and $D _ { t _ { 0 } }$ to be $> n ( n - 2 )$, contradicting the Bezout theorem because $C$ is irreducible and $D _ { t _ { 0 } }$ has smaller degree.
points, counted properly. In the proper counting a double point of $C$ should be counted twice. Thus, the number of free points in which $C$ meets a curve $D$ of degree $n - 2$ passing through the $( n - 1 ) ( n - 2 ) / 2$ double points of $C$ is $n ( n - 2 ) - ( n - 1 ) ( n - 2 ) = n - 2$. Since $n - 2$ is also the dimension of the system $S$, the members of $S$ which pass through $n - 3$ fixed simple points of $C$ form a pencil, i.e., a one-parameter family $D _ { t }$, a variable member of which meets $C$ in one variable point whose coordinates are single-valued, and hence rational, functions of $t$. If $C$ had an extra double point, then one can take a value $t_0$ of $t$ so that $D _ { t _ { 0 } }$ goes through it and this would make the properly counted intersections of $C$ and $D _ { t _ { 0 } }$ to be $> n ( n - 2 )$, contradicting the Bezout theorem because $C$ is irreducible and $D _ { t _ { 0 } }$ has smaller degree.