Difference between revisions of "Witt theorem"
m (link) |
Ulf Rehmann (talk | contribs) m (tex encoded by computer) |
||
| Line 1: | Line 1: | ||
| − | + | <!-- | |
| + | w0980901.png | ||
| + | $#A+1 = 35 n = 1 | ||
| + | $#C+1 = 35 : ~/encyclopedia/old_files/data/W098/W.0908090 Witt theorem | ||
| + | Automatically converted into TeX, above some diagnostics. | ||
| + | Please remove this comment and the {{TEX|auto}} line below, | ||
| + | if TeX found to be correct. | ||
| + | --> | ||
| − | + | {{TEX|auto}} | |
| + | {{TEX|done}} | ||
| − | + | Any isometry between two subspaces $ F _ {1} $ | |
| + | and $ F _ {2} $ | ||
| + | of a finite-dimensional [[Vector space|vector space]] $ V $, | ||
| + | defined over a field $ k $ | ||
| + | of characteristic different from 2 and provided with a metric structure induced from a non-degenerate symmetric or skew-symmetric [[Bilinear form|bilinear form]] $ f $, | ||
| + | may be extended to a metric automorphism of the entire space $ V $. | ||
| + | The theorem was first obtained by E. Witt [[#References|[1]]]. | ||
| − | (property | + | Witt's theorem may also be proved under wider assumptions on $ k $ |
| + | and $ f $[[#References|[2]]], [[#References|[3]]]. In fact, the theorem remains valid if $ k $ | ||
| + | is a skew-field, $ V $ | ||
| + | is a finite-dimensional left $ k $- | ||
| + | module and $ f $ | ||
| + | is a non-degenerate $ \epsilon $- | ||
| + | Hermitian form (with respect to some fixed involutory [[anti-automorphism]] $ \sigma $ | ||
| + | of $ k $, | ||
| + | cf. [[Hermitian form|Hermitian form]]) satisfying the following condition: For any $ v \in V $ | ||
| + | there exists an element $ \alpha \in k $ | ||
| + | such that | ||
| + | |||
| + | $$ | ||
| + | f ( v, v) = \alpha + \epsilon \alpha ^ \sigma | ||
| + | $$ | ||
| + | |||
| + | (property $ ( T) $). | ||
| + | Property $ ( T) $ | ||
| + | holds if, for example, $ f $ | ||
| + | is a Hermitian form and the characteristic of $ k $ | ||
| + | is different from 2, or if $ f $ | ||
| + | is an alternating form. Witt's theorem is also valid if $ k $ | ||
| + | is a field and $ f $ | ||
| + | is the symmetric bilinear form associated with a non-degenerate [[Quadratic form|quadratic form]] $ Q $ | ||
| + | on $ V $. | ||
| + | It follows from Witt's theorem that the group of metric automorphisms of $ V $ | ||
| + | transitively permutes the totally-isotropic subspaces of the same dimension and that all maximal totally-isotropic subspaces in $ V $ | ||
| + | have the same dimension (the Witt index of $ f $). | ||
| + | A second consequence of Witt's theorem may be stated as follows: The isometry classes of non-degenerate symmetric bilinear forms of finite rank over $ k $ | ||
| + | with direct orthogonal sum form a monoid with cancellation; the canonical mapping of this monoid into its [[Grothendieck group|Grothendieck group]] is injective. The group $ \mathop{\rm WG} ( k) $ | ||
| + | is called the Witt–Grothendieck group $ \mathop{\rm WG} ( k) $ | ||
| + | of $ k $; | ||
| + | the tensor product of forms induces on it the structure of a ring, which is known as the Witt–Grothendieck of $ k $[[#References|[7]]]. | ||
For other applications of Witt's theorem see [[Witt decomposition|Witt decomposition]]; [[Witt ring|Witt ring]]. | For other applications of Witt's theorem see [[Witt decomposition|Witt decomposition]]; [[Witt ring|Witt ring]]. | ||
Revision as of 08:29, 6 June 2020
Any isometry between two subspaces $ F _ {1} $
and $ F _ {2} $
of a finite-dimensional vector space $ V $,
defined over a field $ k $
of characteristic different from 2 and provided with a metric structure induced from a non-degenerate symmetric or skew-symmetric bilinear form $ f $,
may be extended to a metric automorphism of the entire space $ V $.
The theorem was first obtained by E. Witt [1].
Witt's theorem may also be proved under wider assumptions on $ k $ and $ f $[2], [3]. In fact, the theorem remains valid if $ k $ is a skew-field, $ V $ is a finite-dimensional left $ k $- module and $ f $ is a non-degenerate $ \epsilon $- Hermitian form (with respect to some fixed involutory anti-automorphism $ \sigma $ of $ k $, cf. Hermitian form) satisfying the following condition: For any $ v \in V $ there exists an element $ \alpha \in k $ such that
$$ f ( v, v) = \alpha + \epsilon \alpha ^ \sigma $$
(property $ ( T) $). Property $ ( T) $ holds if, for example, $ f $ is a Hermitian form and the characteristic of $ k $ is different from 2, or if $ f $ is an alternating form. Witt's theorem is also valid if $ k $ is a field and $ f $ is the symmetric bilinear form associated with a non-degenerate quadratic form $ Q $ on $ V $. It follows from Witt's theorem that the group of metric automorphisms of $ V $ transitively permutes the totally-isotropic subspaces of the same dimension and that all maximal totally-isotropic subspaces in $ V $ have the same dimension (the Witt index of $ f $). A second consequence of Witt's theorem may be stated as follows: The isometry classes of non-degenerate symmetric bilinear forms of finite rank over $ k $ with direct orthogonal sum form a monoid with cancellation; the canonical mapping of this monoid into its Grothendieck group is injective. The group $ \mathop{\rm WG} ( k) $ is called the Witt–Grothendieck group $ \mathop{\rm WG} ( k) $ of $ k $; the tensor product of forms induces on it the structure of a ring, which is known as the Witt–Grothendieck of $ k $[7].
For other applications of Witt's theorem see Witt decomposition; Witt ring.
References
| [1] | E. Witt, "Theorie der quadratischen formen in beliebigen Körpern" J. Reine Angew. Math. , 176 (1937) pp. 31–44 Zbl 0015.05701 Zbl 62.0106.02 |
| [2] | N. Bourbaki, "Elements of mathematics. Algebra: Algebraic structures. Linear algebra" , Elements of mathematics , 1 , Addison-Wesley (1974) pp. Chapts. 1–2 (Translated from French) MR0354207 |
| [3] | J.A. Dieudonné, "La géométrie des groups classiques" , Springer (1955) Zbl 0221.20056 |
| [4] | S. Lang, "Algebra" , Addison-Wesley (1974) MR0783636 Zbl 0712.00001 |
| [5] | E. Artin, "Geometric algebra" , Interscience (1957) MR1529733 MR0082463 Zbl 0077.02101 |
| [6] | J.-P. Serre, "A course in arithmetic" , Springer (1973) (Translated from French) MR0344216 Zbl 0256.12001 |
| [7] | J. Milnor, "Algebraic 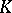 -theory and quadratic forms" Invent. Math. , 9 (1969/70) pp. 318–344 -theory and quadratic forms" Invent. Math. , 9 (1969/70) pp. 318–344 |
Witt theorem. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Witt_theorem&oldid=49234