Difference between revisions of "Leopoldt conjecture"
Ulf Rehmann (talk | contribs) m (MR/ZBL numbers added) |
Ulf Rehmann (talk | contribs) m (tex encoded by computer) |
||
| Line 1: | Line 1: | ||
| − | + | <!-- | |
| + | l1101201.png | ||
| + | $#A+1 = 71 n = 4 | ||
| + | $#C+1 = 71 : ~/encyclopedia/old_files/data/L110/L.1100120 Leopoldt conjecture | ||
| + | Automatically converted into TeX, above some diagnostics. | ||
| + | Please remove this comment and the {{TEX|auto}} line below, | ||
| + | if TeX found to be correct. | ||
| + | --> | ||
| − | + | {{TEX|auto}} | |
| + | {{TEX|done}} | ||
| − | + | Let $ F $ | |
| + | be a totally real algebraic number field (cf. also [[Field|Field]]; [[Algebraic number|Algebraic number]]) and let $ p $ | ||
| + | be a prime number. Let $ {\sigma _ {1} \dots \sigma _ {r _ {1} } } : F \rightarrow {\mathbf C _ {p} } $ | ||
| + | denote the distinct embeddings of $ F $ | ||
| + | into the completion $ \mathbf C _ {p} $ | ||
| + | of the algebraic closure of $ \mathbf Q _ {p} $. | ||
| + | By the Dirichlet unit theorem (cf. also [[Dirichlet theorem|Dirichlet theorem]]), the unit group $ U _ {F} $ | ||
| + | of $ F $ | ||
| + | has rank $ r = r _ {1} - 1 $. | ||
| + | Let $ \epsilon _ {1} \dots \epsilon _ {r} $ | ||
| + | be a $ \mathbf Z $- | ||
| + | basis of $ U _ {F} $. | ||
| + | In [[#References|[a5]]], H.-W. Leopoldt defined the $ p $- | ||
| + | adic regulator $ R _ {p} ( F ) $ | ||
| + | as the $ p $- | ||
| + | adic analogue of the Dirichlet regulator: | ||
| − | + | $$ | |
| + | R _ {p} ( F ) = \pm { \mathop{\rm det} } \left ( { \mathop{\rm log} } _ {p} ( \sigma _ {i} ( \epsilon _ {j} ) ) _ {1 \leq i,j \leq r } \right ) , | ||
| + | $$ | ||
| − | + | where $ { { \mathop{\rm log} } _ {p} } : {U _ {F} } \rightarrow {\mathbf C _ {p} } $ | |
| + | denotes the $ p $- | ||
| + | adic logarithm. | ||
| − | + | Leopoldt's conjecture is: $ R _ {p} ( F ) \neq 0 $. | |
| − | + | The definition of $ R _ {p} ( F ) $( | |
| + | and therefore also the conjecture) extends to arbitrary number fields (cf. [[#References|[a7]]]) and is nowadays considered in this generality. A. Brumer used transcendental methods developed by A. Baker to prove Leopoldt's conjecture for fields $ F $ | ||
| + | that are Abelian over $ \mathbf Q $ | ||
| + | or over an imaginary quadratic field [[#References|[a2]]]. For specific non-Abelian fields the conjecture has also been verified (cf., e.g., [[#References|[a1]]]), but in general it is still (1996) open. | ||
| − | + | For a totally real field $ F $, | |
| + | Leopoldt's conjecture is equivalent to the non-vanishing of the $ p $- | ||
| + | adic $ \zeta $- | ||
| + | function $ \zeta _ {F,p } ( s ) $ | ||
| + | at $ s = 1 $( | ||
| + | cf. [[#References|[a5]]], [[#References|[a3]]]). | ||
| − | and the Leopoldt defect | + | For a prime $ v $ |
| + | in $ F $, | ||
| + | let $ U _ {v} $ | ||
| + | denote the group of units of the local field $ F _ {v} $. | ||
| + | There is a canonical mapping | ||
| + | |||
| + | $$ | ||
| + | {f _ {p} } : {U _ {F} \otimes \mathbf Z _ {p} } \rightarrow {\prod _ { {v \mid p } } U _ {v} } | ||
| + | $$ | ||
| + | |||
| + | and the Leopoldt defect $ \delta _ {F} $ | ||
| + | is defined as the $ \mathbf Z _ {p} $- | ||
| + | rank of $ { \mathop{\rm ker} } f _ {p} $. | ||
| + | [[Class field theory|Class field theory]] yields the following equivalent formulation of the Leopoldt conjecture (cf. [[#References|[a7]]]): Leopoldt's conjecture holds if and only if $ \delta _ {F} = 0 $. | ||
==Relation to Iwasawa theory.== | ==Relation to Iwasawa theory.== | ||
| − | An extension | + | An extension $ F _ \infty /F $ |
| + | of a number field $ F $ | ||
| + | is called a $ \mathbf Z _ {p} $- | ||
| + | extension if it is a [[Galois extension|Galois extension]] and $ { \mathop{\rm Gal} } ( F _ \infty /F ) \cong \mathbf Z _ {p} $. | ||
| + | The number of independent $ \mathbf Z _ {p} $- | ||
| + | extensions of $ F $ | ||
| + | is related via class field theory to the $ \mathbf Z _ {p} $- | ||
| + | rank of $ { \mathop{\rm coker} } f _ {p} $ | ||
| + | and is equal to $ 1 + r _ {2} ( F ) + \delta _ {F} $( | ||
| + | cf. [[#References|[a4]]]), where $ r _ {2} ( F ) $ | ||
| + | is the number of pairs of complex-conjugate embeddings of $ F $. | ||
| − | For | + | For $ n \geq 0 $, |
| + | let $ F _ {n} $ | ||
| + | denote the unique subfield of $ F _ \infty /F $ | ||
| + | of degree $ p ^ {n} $ | ||
| + | over $ F $ | ||
| + | and let $ \delta _ {n} $ | ||
| + | denote the Leopoldt defect of $ F _ {n} $. | ||
| + | The $ \mathbf Z _ {p} $- | ||
| + | extension $ F _ \infty /F $ | ||
| + | satisfies the weak Leopoldt conjecture if the defects $ \delta _ {n} $ | ||
| + | are bounded independent of $ n $. | ||
| + | It is known (cf. [[#References|[a4]]]) that the weak Leopoldt conjecture holds for the so-called cyclotomic $ \mathbf Z _ {p} $- | ||
| + | extension of $ F $, | ||
| + | i.e. for the unique $ \mathbf Z _ {p} $- | ||
| + | extension contained in $ F ( \mu _ {p ^ \infty } ) $. | ||
==Relation to Galois cohomology.== | ==Relation to Galois cohomology.== | ||
| − | Let | + | Let $ G _ {p} ( F ) $ |
| + | denote the [[Galois group|Galois group]] of the maximal pro- $ p $- | ||
| + | extension of $ F $, | ||
| + | which is unramified outside $ p $. | ||
| + | Leopoldt's conjecture is equivalent to the vanishing of the [[Galois cohomology|Galois cohomology]] group $ H ^ {2} ( G _ {p} ( F ) , \mathbf Q _ {p} / \mathbf Z _ {p} ) $[[#References|[a6]]]. More generally, it is conjectured that | ||
| − | + | $$ | |
| + | H ^ {2} ( G _ {p} ( F ) , \mathbf Q _ {p} / \mathbf Z _ {p} ( i ) ) = 0 | ||
| + | $$ | ||
| − | for all | + | for all $ i \neq 1 $[[#References|[a6]]]. This is known to be true for $ i \geq 2 $ |
| + | as a consequence of a profound result of A. Borel in [[Algebraic K-theory|algebraic $ K $- | ||
| + | theory]]. | ||
====References==== | ====References==== | ||
<table><TR><TD valign="top">[a1]</TD> <TD valign="top"> F. Bertrandias, J.-J. Payan, "<img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/l/l110/l110120/l11012078.png" />-extensions et invariants cyclotomiques" ''Ann. Sci. Ecole Norm. Sup. (4)'' , '''5''' (1972) pp. 517–543 {{MR|0480419}} {{MR|0337882}} {{ZBL|0246.12005}} {{ZBL|0246.12004}} </TD></TR><TR><TD valign="top">[a2]</TD> <TD valign="top"> A. Brumer, "On the units of algebraic number fields" ''Mathematica'' , '''14''' (1967) pp. 121–124 {{MR|0220694}} {{ZBL|0171.01105}} </TD></TR><TR><TD valign="top">[a3]</TD> <TD valign="top"> P. Colmez, "Résidu en <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/l/l110/l110120/l11012079.png" /> des fonctions zêta <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/l/l110/l110120/l11012080.png" />-adiques" ''Invent. Math.'' , '''91''' (1988) pp. 371–389</TD></TR><TR><TD valign="top">[a4]</TD> <TD valign="top"> K. Iwasawa, "On <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/l/l110/l110120/l11012081.png" />-extensions of algebraic number fields" ''Ann. of Math.'' , '''98''' (1973) pp. 246–326 {{MR|349627}} {{ZBL|}} </TD></TR><TR><TD valign="top">[a5]</TD> <TD valign="top"> H.-W. Leopoldt, "Zur Arithmetik in abelschen Zahlkörpern" ''J. Reine Angew. Math.'' , '''209''' (1962) pp. 54–71 {{MR|0139602}} {{ZBL|0204.07101}} </TD></TR><TR><TD valign="top">[a6]</TD> <TD valign="top"> P. Schneider, "Über gewisse Galoiscohomologiegruppen" ''Math. Z.'' , '''168''' (1979) pp. 181–205 {{MR|0544704}} {{ZBL|0421.12024}} </TD></TR><TR><TD valign="top">[a7]</TD> <TD valign="top"> L.C. Washington, "Introduction to cyclotomic fields" , Springer (1982) {{MR|0718674}} {{ZBL|0484.12001}} </TD></TR></table> | <table><TR><TD valign="top">[a1]</TD> <TD valign="top"> F. Bertrandias, J.-J. Payan, "<img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/l/l110/l110120/l11012078.png" />-extensions et invariants cyclotomiques" ''Ann. Sci. Ecole Norm. Sup. (4)'' , '''5''' (1972) pp. 517–543 {{MR|0480419}} {{MR|0337882}} {{ZBL|0246.12005}} {{ZBL|0246.12004}} </TD></TR><TR><TD valign="top">[a2]</TD> <TD valign="top"> A. Brumer, "On the units of algebraic number fields" ''Mathematica'' , '''14''' (1967) pp. 121–124 {{MR|0220694}} {{ZBL|0171.01105}} </TD></TR><TR><TD valign="top">[a3]</TD> <TD valign="top"> P. Colmez, "Résidu en <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/l/l110/l110120/l11012079.png" /> des fonctions zêta <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/l/l110/l110120/l11012080.png" />-adiques" ''Invent. Math.'' , '''91''' (1988) pp. 371–389</TD></TR><TR><TD valign="top">[a4]</TD> <TD valign="top"> K. Iwasawa, "On <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/l/l110/l110120/l11012081.png" />-extensions of algebraic number fields" ''Ann. of Math.'' , '''98''' (1973) pp. 246–326 {{MR|349627}} {{ZBL|}} </TD></TR><TR><TD valign="top">[a5]</TD> <TD valign="top"> H.-W. Leopoldt, "Zur Arithmetik in abelschen Zahlkörpern" ''J. Reine Angew. Math.'' , '''209''' (1962) pp. 54–71 {{MR|0139602}} {{ZBL|0204.07101}} </TD></TR><TR><TD valign="top">[a6]</TD> <TD valign="top"> P. Schneider, "Über gewisse Galoiscohomologiegruppen" ''Math. Z.'' , '''168''' (1979) pp. 181–205 {{MR|0544704}} {{ZBL|0421.12024}} </TD></TR><TR><TD valign="top">[a7]</TD> <TD valign="top"> L.C. Washington, "Introduction to cyclotomic fields" , Springer (1982) {{MR|0718674}} {{ZBL|0484.12001}} </TD></TR></table> | ||
Revision as of 22:16, 5 June 2020
Let $ F $
be a totally real algebraic number field (cf. also Field; Algebraic number) and let $ p $
be a prime number. Let $ {\sigma _ {1} \dots \sigma _ {r _ {1} } } : F \rightarrow {\mathbf C _ {p} } $
denote the distinct embeddings of $ F $
into the completion $ \mathbf C _ {p} $
of the algebraic closure of $ \mathbf Q _ {p} $.
By the Dirichlet unit theorem (cf. also Dirichlet theorem), the unit group $ U _ {F} $
of $ F $
has rank $ r = r _ {1} - 1 $.
Let $ \epsilon _ {1} \dots \epsilon _ {r} $
be a $ \mathbf Z $-
basis of $ U _ {F} $.
In [a5], H.-W. Leopoldt defined the $ p $-
adic regulator $ R _ {p} ( F ) $
as the $ p $-
adic analogue of the Dirichlet regulator:
$$ R _ {p} ( F ) = \pm { \mathop{\rm det} } \left ( { \mathop{\rm log} } _ {p} ( \sigma _ {i} ( \epsilon _ {j} ) ) _ {1 \leq i,j \leq r } \right ) , $$
where $ { { \mathop{\rm log} } _ {p} } : {U _ {F} } \rightarrow {\mathbf C _ {p} } $ denotes the $ p $- adic logarithm.
Leopoldt's conjecture is: $ R _ {p} ( F ) \neq 0 $.
The definition of $ R _ {p} ( F ) $( and therefore also the conjecture) extends to arbitrary number fields (cf. [a7]) and is nowadays considered in this generality. A. Brumer used transcendental methods developed by A. Baker to prove Leopoldt's conjecture for fields $ F $ that are Abelian over $ \mathbf Q $ or over an imaginary quadratic field [a2]. For specific non-Abelian fields the conjecture has also been verified (cf., e.g., [a1]), but in general it is still (1996) open.
For a totally real field $ F $, Leopoldt's conjecture is equivalent to the non-vanishing of the $ p $- adic $ \zeta $- function $ \zeta _ {F,p } ( s ) $ at $ s = 1 $( cf. [a5], [a3]).
For a prime $ v $ in $ F $, let $ U _ {v} $ denote the group of units of the local field $ F _ {v} $. There is a canonical mapping
$$ {f _ {p} } : {U _ {F} \otimes \mathbf Z _ {p} } \rightarrow {\prod _ { {v \mid p } } U _ {v} } $$
and the Leopoldt defect $ \delta _ {F} $ is defined as the $ \mathbf Z _ {p} $- rank of $ { \mathop{\rm ker} } f _ {p} $. Class field theory yields the following equivalent formulation of the Leopoldt conjecture (cf. [a7]): Leopoldt's conjecture holds if and only if $ \delta _ {F} = 0 $.
Relation to Iwasawa theory.
An extension $ F _ \infty /F $ of a number field $ F $ is called a $ \mathbf Z _ {p} $- extension if it is a Galois extension and $ { \mathop{\rm Gal} } ( F _ \infty /F ) \cong \mathbf Z _ {p} $. The number of independent $ \mathbf Z _ {p} $- extensions of $ F $ is related via class field theory to the $ \mathbf Z _ {p} $- rank of $ { \mathop{\rm coker} } f _ {p} $ and is equal to $ 1 + r _ {2} ( F ) + \delta _ {F} $( cf. [a4]), where $ r _ {2} ( F ) $ is the number of pairs of complex-conjugate embeddings of $ F $.
For $ n \geq 0 $, let $ F _ {n} $ denote the unique subfield of $ F _ \infty /F $ of degree $ p ^ {n} $ over $ F $ and let $ \delta _ {n} $ denote the Leopoldt defect of $ F _ {n} $. The $ \mathbf Z _ {p} $- extension $ F _ \infty /F $ satisfies the weak Leopoldt conjecture if the defects $ \delta _ {n} $ are bounded independent of $ n $. It is known (cf. [a4]) that the weak Leopoldt conjecture holds for the so-called cyclotomic $ \mathbf Z _ {p} $- extension of $ F $, i.e. for the unique $ \mathbf Z _ {p} $- extension contained in $ F ( \mu _ {p ^ \infty } ) $.
Relation to Galois cohomology.
Let $ G _ {p} ( F ) $ denote the Galois group of the maximal pro- $ p $- extension of $ F $, which is unramified outside $ p $. Leopoldt's conjecture is equivalent to the vanishing of the Galois cohomology group $ H ^ {2} ( G _ {p} ( F ) , \mathbf Q _ {p} / \mathbf Z _ {p} ) $[a6]. More generally, it is conjectured that
$$ H ^ {2} ( G _ {p} ( F ) , \mathbf Q _ {p} / \mathbf Z _ {p} ( i ) ) = 0 $$
for all $ i \neq 1 $[a6]. This is known to be true for $ i \geq 2 $ as a consequence of a profound result of A. Borel in algebraic $ K $- theory.
References
| [a1] | F. Bertrandias, J.-J. Payan, "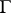 -extensions et invariants cyclotomiques" Ann. Sci. Ecole Norm. Sup. (4) , 5 (1972) pp. 517–543 MR0480419 MR0337882 Zbl 0246.12005 Zbl 0246.12004 -extensions et invariants cyclotomiques" Ann. Sci. Ecole Norm. Sup. (4) , 5 (1972) pp. 517–543 MR0480419 MR0337882 Zbl 0246.12005 Zbl 0246.12004 |
| [a2] | A. Brumer, "On the units of algebraic number fields" Mathematica , 14 (1967) pp. 121–124 MR0220694 Zbl 0171.01105 |
| [a3] | P. Colmez, "Résidu en 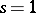 des fonctions zêta des fonctions zêta 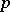 -adiques" Invent. Math. , 91 (1988) pp. 371–389 -adiques" Invent. Math. , 91 (1988) pp. 371–389 |
| [a4] | K. Iwasawa, "On 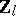 -extensions of algebraic number fields" Ann. of Math. , 98 (1973) pp. 246–326 MR349627 -extensions of algebraic number fields" Ann. of Math. , 98 (1973) pp. 246–326 MR349627 |
| [a5] | H.-W. Leopoldt, "Zur Arithmetik in abelschen Zahlkörpern" J. Reine Angew. Math. , 209 (1962) pp. 54–71 MR0139602 Zbl 0204.07101 |
| [a6] | P. Schneider, "Über gewisse Galoiscohomologiegruppen" Math. Z. , 168 (1979) pp. 181–205 MR0544704 Zbl 0421.12024 |
| [a7] | L.C. Washington, "Introduction to cyclotomic fields" , Springer (1982) MR0718674 Zbl 0484.12001 |
Leopoldt conjecture. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Leopoldt_conjecture&oldid=47614