Difference between revisions of "Geometry of immersed manifolds"
(Importing text file) |
Ulf Rehmann (talk | contribs) m (tex encoded by computer) |
||
| Line 1: | Line 1: | ||
| − | + | <!-- | |
| + | g0443401.png | ||
| + | $#A+1 = 324 n = 5 | ||
| + | $#C+1 = 324 : ~/encyclopedia/old_files/data/G044/G.0404340 Geometry of immersed manifolds | ||
| + | Automatically converted into TeX, above some diagnostics. | ||
| + | Please remove this comment and the {{TEX|auto}} line below, | ||
| + | if TeX found to be correct. | ||
| + | --> | ||
| − | + | {{TEX|auto}} | |
| + | {{TEX|done}} | ||
| − | + | A theory that deals with the extrinsic geometry and the relation between the extrinsic and intrinsic geometry (cf. also [[Interior geometry|Interior geometry]]) of submanifolds in a Euclidean or Riemannian space. The geometry of immersed manifolds is a generalization of the classical differential geometry of surfaces in the Euclidean space $ \mathbf R ^ {3} $. | |
| + | The intrinsic and extrinsic geometries of an immersed manifold are usually described locally by means of the first and the second fundamental form, respectively. For immersions of an $ m $- | ||
| + | dimensional manifold $ M ^ {m} $ | ||
| + | in a manifold $ N ^ {n} $ | ||
| + | one has a concept of congruence (see [[Immersion of a manifold|Immersion of a manifold]]). In the geometry of immersed manifolds one examines properties that are identical for congruent immersions, i.e. properties of a surface $ F ^ { m } $ | ||
| + | defined by an immersion $ f $. | ||
| + | In this connection, an immersion and a surface are not distinguished from the geometrical point of view. An immersion $ f $ | ||
| + | induces a mapping $ df: TM ^ {m} \rightarrow TN ^ {n} $ | ||
| + | of the tangent bundles (cf. [[Tangent bundle|Tangent bundle]]). | ||
| − | + | The first quadratic (fundamental) form $ g $ | |
| + | of a submanifold $ F $ | ||
| + | is defined on $ TM ^ {m} $ | ||
| + | by | ||
| − | + | $$ | |
| + | g _ {p} ( X, Y) = \overline{g}\; _ {f( g) } ( X, Y), | ||
| + | $$ | ||
| − | where | + | where $ p \in M ^ {m} $, |
| + | $ X, Y \in TM ^ {m} $ | ||
| + | and $ \overline{g}\; $ | ||
| + | is a Riemannian metric on $ N ^ {n} $. | ||
| + | Here and subsequently, the vectors $ X \in TM ^ {m} $ | ||
| + | are not distinguished in symbols from their image $ df( X) $. | ||
| + | The quadratic form $ g $ | ||
| + | defines the structure of a Riemannian space $ M _ {g} ^ {m} $ | ||
| + | on $ M ^ {m} $; | ||
| + | the properties of $ M _ {g} ^ {m} $ | ||
| + | constitute the subject of the intrinsic geometry of the submanifold $ F $. | ||
| + | If $ \{ x ^ {k} \} $, | ||
| + | $ \{ y ^ \alpha \} $, | ||
| + | $ k = 1 \dots m $, | ||
| + | $ \alpha = 1 \dots n $, | ||
| + | are local coordinates in $ M ^ {m} $ | ||
| + | and $ N ^ {n} $, | ||
| + | the immersion $ f $ | ||
| + | is given by the parametric equations $ y ^ \alpha = f ^ \alpha ( x ^ {1} \dots x ^ {m} ) $. | ||
| + | In local coordinates | ||
| − | + | $$ | |
| + | g _ {p} ( X, Y) = g _ {ij} ( p) X ^ {i} Y ^ {j} , | ||
| + | $$ | ||
| − | and | + | where $ \{ X ^ {i} \} $ |
| + | and $ \{ Y ^ {j} \} $ | ||
| + | are the components of the vectors $ X $ | ||
| + | and $ Y $, | ||
| − | + | $$ | |
| + | g _ {ij} = \overline{g}\; _ {\alpha \beta } | ||
| + | \frac{\partial f _ \alpha }{\partial x | ||
| + | ^ {i} } | ||
| − | + | \frac{\partial f _ \beta }{\partial x ^ {j} } | |
| + | , | ||
| + | $$ | ||
| − | + | and $ \{ \overline{g}\; _ {\alpha \beta } \} $ | |
| + | are the components of the metric tensor $ \overline{g}\; $ | ||
| + | of the Riemannian space $ N ^ {n} $. | ||
| − | + | Concepts such as curve length, volume of a region, Levi-Civita connection $ \nabla _ {X} $ | |
| + | of the intrinsic metric, curvature transformation $ R( X, Y) Z $, | ||
| + | etc., relate to the intrinsic geometry of $ F $. | ||
| + | The computational formulas applying here can be consulted in [[Riemannian geometry|Riemannian geometry]]. | ||
| − | + | The second (fundamental) tensor (form) $ H $ | |
| + | is defined by | ||
| − | + | $$ | |
| + | H( X, Y) _ {p} = ( \overline \nabla \; _ {X} Y) _ {p} - (\nabla _ {X} Y) _ {p} , | ||
| + | $$ | ||
| − | + | where $ \overline \nabla \; $ | |
| + | and $ \nabla $ | ||
| + | are the Levi-Civita connections in $ N ^ {n} $ | ||
| + | and $ M ^ {m} $, | ||
| + | respectively. In fact, $ H $ | ||
| + | is not dependent on the vector fields $ X $ | ||
| + | and $ Y $ | ||
| + | but only on their values at the point $ p $ | ||
| + | and is a bilinear symmetric mapping | ||
| − | + | $$ | |
| + | ( TM ^ {m} ) _ {p} \times ( TM ^ {m} ) _ {p} \rightarrow ( \nu M ^ {m} ) _ {p} , | ||
| + | $$ | ||
| − | + | where $ \nu M ^ {m} $ | |
| + | is the [[Normal bundle|normal bundle]] of $ M ^ {m} $ | ||
| + | in $ N ^ {n} $. | ||
| + | For each unit vector $ \xi \in ( \nu M ^ {m} ) _ {p} $, | ||
| + | the equations | ||
| − | + | $$ | |
| + | \langle H ( X, Y), \xi \rangle _ {p} = h _ \xi ( X, Y) _ {p} = \ | ||
| + | \langle A _ \xi ( X), Y \rangle _ {p} $$ | ||
| − | One defines the principal curvature, principal direction in the direction of | + | define the second quadratic form (or second fundamental form) $ h _ \xi $ |
| + | and the shape operator $ A _ \xi $ | ||
| + | in the direction of $ \xi $. | ||
| + | In local coordinates the components $ h _ {ij} ( \xi ) $ | ||
| + | of the form $ h _ \xi $ | ||
| + | are | ||
| + | |||
| + | $$ | ||
| + | h _ {ij} ( \xi ) = \ | ||
| + | \overline{g}\; _ {\alpha \beta } | ||
| + | \frac{\partial ^ {2} f ^ { \alpha } }{\partial x | ||
| + | ^ {i} \partial x ^ {j} } | ||
| + | \xi ^ \beta , | ||
| + | $$ | ||
| + | |||
| + | where $ \{ \xi ^ \beta \} $ | ||
| + | are the components of $ \xi $. | ||
| + | |||
| + | One defines the principal curvature, principal direction in the direction of $ \xi $, | ||
| + | and other related concepts for the form $ h _ \xi $ | ||
| + | in the usual way (i.e. as for a surface in the Euclidean space $ \mathbf R ^ {3} $). | ||
Using elementary symmetric functions, one can construct various principal-curvature functions, such as, for example, the mean curvature | Using elementary symmetric functions, one can construct various principal-curvature functions, such as, for example, the mean curvature | ||
| − | + | $$ | |
| + | H = | ||
| + | \frac{1}{m} | ||
| + | \sqrt {\sum _ {j= 1 } ^ { {m+ } n } \left ( \sum _ {i= 1 } ^ { m } | ||
| + | K _ {i} ( \xi _ {j} ) \right ) ^ {2} } , | ||
| + | $$ | ||
| − | where | + | where $ \{ \xi _ {i} \} $ |
| + | is an orthonormal set of normals and $ K _ {i} ( \xi ) $ | ||
| + | are the principal curvatures of the forms $ h _ {i} $; | ||
| + | the Chern–Lashof curvature | ||
| − | + | $$ | |
| + | K = | ||
| + | \frac{1}{\omega _ {n- m- 1 } } | ||
| + | \int\limits _ {\xi \in S ^ {n- m- 1 } } | | ||
| + | K _ {1} ( \xi ) \dots K _ {m} ( \xi ) | d \sigma , | ||
| + | $$ | ||
| − | where | + | where $ \omega _ {l} $ |
| + | is the volume of the sphere $ S ^ {l} $; | ||
| + | and also the length of the second fundamental form | ||
| − | + | $$ | |
| + | S = \sqrt {\sum _ { i,j } K _ {i} ^ {2} ( \xi _ {j} ) } | ||
| + | $$ | ||
(see [[#References|[1]]]–[[#References|[3]]]). | (see [[#References|[1]]]–[[#References|[3]]]). | ||
| − | The values of the first and second fundamental forms for a submanifold at a point | + | The values of the first and second fundamental forms for a submanifold at a point $ p $ |
| + | define it near $ p $ | ||
| + | infinitesimally up to small quantities of the second order. Each $ \xi \in ( \nu M ^ {m} ) _ {p} $, | ||
| + | $ | \xi | = 1 $, | ||
| + | corresponds to an osculating paraboloid (for a submanifold in a Euclidean space, this is the osculating paraboloid for the projection of the submanifold on the $ ( m+ 1) $- | ||
| + | dimensional plane defined by $ ( TM ^ {m} ) _ {p} $ | ||
| + | and $ \xi $). | ||
| + | If $ m = n- 1 $( | ||
| + | i.e. in the case of a hypersurface), the form $ h _ \xi $ | ||
| + | is unique up to sign. In that case, the second fundamental tensor and the second fundamental form do not differ, and the theory acquires considerable similarity with the classical theory of surfaces in $ \mathbf R ^ {3} $. | ||
==Basic equations.== | ==Basic equations.== | ||
| − | The basic equations for an immersed manifold, i.e. the Gauss equations, the Codazzi–Mainardi equations and the Ricci equations, relate the first and second fundamental forms and the curvature tensors of | + | The basic equations for an immersed manifold, i.e. the Gauss equations, the Codazzi–Mainardi equations and the Ricci equations, relate the first and second fundamental forms and the curvature tensors of $ M $ |
| + | and $ N $. | ||
| + | For each vector field section $ X $ | ||
| + | over $ M $ | ||
| + | of the vector bundle $ TN $ | ||
| + | restricted to $ M $, | ||
| + | let $ t ( X) $ | ||
| + | denote the tangential component and $ n ( X) $ | ||
| + | the normal component. The Gauss formula defining the second fundamental form, | ||
| − | + | $$ | |
| + | \overline \nabla \; _ {X} Y = \nabla _ {X} Y + H ( X , Y ), | ||
| + | $$ | ||
| − | gives the normal-tangent decomposition of | + | gives the normal-tangent decomposition of $ \overline \nabla \; _ {X} Y $ |
| + | for $ X , Y $ | ||
| + | vector fields on $ M $. | ||
| + | The Weingarten formula (defining the shape operator), | ||
| − | + | $$ | |
| + | \overline \nabla \; _ {X} \xi = - A _ \xi X + D _ {X} \xi , | ||
| + | $$ | ||
| − | does the same in case | + | does the same in case $ X $ |
| + | is a vector field on $ M $ | ||
| + | and the section $ \xi $ | ||
| + | of $ TN $ | ||
| + | is normal to $ M $. | ||
| + | In terms of the shape operators and the second fundamental form one finds that for three vector fields $ X $, | ||
| + | $ Y $, | ||
| + | $ Z $ | ||
| + | on $ M $ | ||
| + | the tangential component of $ \overline{R}\; ( X , Y ) Z $ | ||
| + | is equal to | ||
| − | + | $$ | |
| + | t ( \overline{R}\; ( X , Y ) Z ) = \ | ||
| + | R ( X , Y ) Z + A _ {H ( X , Z ) } ( Y) - A _ {H ( Y , Z ) } ( X) . | ||
| + | $$ | ||
| − | Taking a fourth vector field | + | Taking a fourth vector field $ W $ |
| + | on $ M $ | ||
| + | this leads to the Gauss equations | ||
| − | + | $$ \tag{1 } | |
| + | \langle \overline{R}\; ( X , Y ) Z , W \rangle = | ||
| + | $$ | ||
| − | + | $$ | |
| + | = \ | ||
| + | \langle R ( X , Y ) Z , W \rangle + | ||
| + | $$ | ||
| − | + | $$ | |
| + | + | ||
| + | \langle H ( X , Z ) , H ( Y , W ) \rangle - \langle H ( Y , Z ) , H ( X , W ) \rangle . | ||
| + | $$ | ||
| − | The normal component of | + | The normal component of $ \overline{R}\; ( X , Y ) Z $ |
| + | is equal to | ||
| − | + | $$ \tag{2 } | |
| + | n ( \overline{R}\; ( X , Y ) Z ) = | ||
| + | $$ | ||
| − | + | $$ | |
| + | = \ | ||
| + | D _ {X} H ( Y , Z ) - D _ {Y} H ( X , Z ) + | ||
| + | $$ | ||
| − | + | $$ | |
| + | + | ||
| + | H ( X , \nabla _ {Y} Z ) - H ( Y , \nabla _ {X} Z ) - H ( [ X , Y ] , Z ) . | ||
| + | $$ | ||
| − | Define the connection | + | Define the connection $ \widetilde \nabla $ |
| + | on the vector bundle $ \mathop{\rm Hom} ( TM \times TM , \nu ( M) ) $, | ||
| + | where $ \nu ( M) $ | ||
| + | is the normal bundle to $ M $ | ||
| + | in $ N $, | ||
| + | by the formula | ||
| − | + | $$ | |
| + | ( \widetilde \nabla _ {X} s ) ( Y , Z ) = \ | ||
| + | D _ {X} ( s ( Y , Z ) ) - | ||
| + | s ( \nabla _ {X} Y , Z ) - s ( Y , \nabla _ {X} Z ) . | ||
| + | $$ | ||
Then (2) can be rewritten as | Then (2) can be rewritten as | ||
| − | + | $$ \tag{2'} | |
| + | n ( \overline{R}\; ( X , Y ) Z ) = \ | ||
| + | ( \widetilde \nabla _ {X} H ) ( Y , Z ) - ( \widetilde \nabla _ {Y} H ) ( X , Z ) . | ||
| + | $$ | ||
| − | Equations (2) (or ( | + | Equations (2) (or (2'})) are the Codazzi–Mainardi equations (in intrinsic form) (cf. also [[Peterson–Codazzi equations|Peterson–Codazzi equations]]). |
| − | Finally, consider the normal component of | + | Finally, consider the normal component of $ \overline{R}\; ( X , Y ) \xi $ |
| + | where $ \xi $ | ||
| + | is a section of $ \nu ( M) $( | ||
| + | by the symmetry properties of $ \overline{R}\; ( W , \xi , X , Y ) = \langle R ( X , Y ) \xi , W \rangle $ | ||
| + | the horizontal component follows from the Codazzi–Mainardi equations). One has | ||
| − | + | $$ \tag{3 } | |
| + | n ( \overline{R}\; ( X , Y ) \xi ) = \ | ||
| + | \widetilde{R} ( X , Y ) \xi - H ( X , A _ \xi Y ) + H ( Y , A _ \xi X ) , | ||
| + | $$ | ||
| − | the Ricci equations. Here | + | the Ricci equations. Here $ \widetilde{R} = R _ {D} $ |
| + | is the curvature tensor of the connection $ D $ | ||
| + | on the normal bundle $ \nu ( M) $. | ||
| + | The Gauss, Codazzi–Mainardi and Ricci equations are the only general equations available for an isometric immersion. It is reasonable to expect something interesting for $ R ( \cdot , \cdot , \cdot , \cdot ) $ | ||
| + | if three of the fields are normal. Indeed, $ ( R ( \xi , \eta ) \xi ) _ {P} $ | ||
| + | then has nothing to do with the immersed manifold $ M $ | ||
| + | at the point $ P $( | ||
| + | except with the point $ P $ | ||
| + | itself). | ||
| − | If the ambient manifold | + | If the ambient manifold $ N $ |
| + | is of constant curvature $ k $, | ||
| + | then $ \overline{R}\; ( X , Y ) Z = k ( \langle Z , Y \rangle X - \langle Z , X \rangle Y ) $ | ||
| + | and so $ \overline{R}\; ( X , Y ) Z $ | ||
| + | is tangent to $ M $. | ||
| + | The Gauss, Ricci and Codazzi–Mainardi equations reduce to | ||
| − | + | $$ \tag{4 } | |
| + | \langle R ( X , Y ) Z , W \rangle = | ||
| + | $$ | ||
| − | + | $$ | |
| + | = \ | ||
| + | k ( \langle X , W > < Y , Z > - < X , Z \rangle \langle Y , W \rangle ) + | ||
| + | $$ | ||
| − | + | $$ | |
| + | + | ||
| + | \langle H ( X , W ) , H ( Y , Z ) \rangle - \langle H ( X , Z ) , H ( Y , W ) \rangle , | ||
| + | $$ | ||
| − | + | $$ \tag{5 } | |
| + | \langle \overline{R}\; ( X , Y ) \xi , \eta \rangle = < \widetilde{R} ( X , Y ) | ||
| + | \xi , \eta > + \langle [ A _ \xi , A _ \eta ] X , Y \rangle , | ||
| + | $$ | ||
| − | where | + | where $ [ A _ \xi , A _ \eta ] = A _ \xi A _ \eta - A _ \eta A _ \xi $, |
| + | and | ||
| − | + | $$ \tag{6 } | |
| + | \widetilde \Delta _ {X} H ( Y , Z ) - \widetilde \Delta _ {Y} H ( X , Z ) = 0 . | ||
| + | $$ | ||
| − | These equations make sense in a more general setting. Indeed, let | + | These equations make sense in a more general setting. Indeed, let $ E $ |
| + | be a Riemannian vector bundle over $ M $, | ||
| + | i.e. there is a (bundle) Riemannian metric $ \langle \cdot , \cdot \rangle _ {E} $ | ||
| + | on $ E $, | ||
| + | and let there be a Riemannian connection $ D : TM \times \Gamma ( E) \rightarrow E $, | ||
| + | where $ \Gamma ( E) $ | ||
| + | denotes the space of smooth sections of $ E $, | ||
| + | which is adapted to the metric. This last phrase means that $ \nabla _ {X} \langle \xi , \eta > = < D _ {X} \xi , \eta \rangle + \langle \xi , D _ {X} \eta \rangle $. | ||
| + | A bilinear mapping $ A : TM \times E \rightarrow TM $ | ||
| + | such that $ A _ \xi : TM \rightarrow TM $ | ||
| + | is self-adjoint for all $ \xi $ | ||
| + | is called a second fundamental tensor in $ E $. | ||
| + | The associated second fundamental form in $ E $ | ||
| + | is then defined by | ||
| − | + | $$ | |
| + | \langle H ( X , Y ) , \xi \rangle _ {E} = \langle A _ \xi X , Y \rangle . | ||
| + | $$ | ||
| − | The three equations (4), (5), (6) make perfect sense in this more general setting. One has now the following generalization of the [[Bonnet theorem|Bonnet theorem]] [[#References|[2]]]: Let | + | The three equations (4), (5), (6) make perfect sense in this more general setting. One has now the following generalization of the [[Bonnet theorem|Bonnet theorem]] [[#References|[2]]]: Let $ M $ |
| + | be a simply-connected Riemannian manifold equipped with a Riemannian vector bundle of dimension $ n $ | ||
| + | with a compatible connection $ D $, | ||
| + | second fundamental tensor $ A $ | ||
| + | and associated second fundamental form $ H $. | ||
| + | Suppose that equations (4), (5), (6) hold. Then there is an isometric immersion of $ M $ | ||
| + | into a simply-connected Riemannian manifold of constant curvature $ k $( | ||
| + | a space form) and dimension $ \mathop{\rm dim} ( M) + n $ | ||
| + | such that the normal bundle is $ E $. | ||
| − | This immersion is unique in the following sense. Let | + | This immersion is unique in the following sense. Let $ f , f ^ { \prime } : M \rightarrow {\mathcal R} ^ {m} ( k) $ |
| + | be two isometric immersions of $ M $ | ||
| + | into a space form $ {\mathcal R} ^ {m} ( k) $ | ||
| + | of curvature $ k $ | ||
| + | and with normal bundles $ E $ | ||
| + | and $ E ^ \prime $, | ||
| + | with their induced bundle metrics, second fundamental forms and connections. Suppose that there is a bundle mapping $ E \rightarrow E ^ \prime $, | ||
| − | + | $$ | |
| − | covering an isometry | + | \begin{array}{lcl} |
| + | E & \mathop \rightarrow \limits ^ \alpha &E ^ \prime \\ | ||
| + | \downarrow &{} &\downarrow \\ | ||
| + | M & \rightarrow _ { g } & M \\ | ||
| + | \end{array} | ||
| + | |||
| + | $$ | ||
| + | |||
| + | covering an isometry $ g $ | ||
| + | of $ M $ | ||
| + | and such that $ \alpha $ | ||
| + | preserves the bundle metrics, connections and second fundamental forms. Then there is a rigid motion $ G $ | ||
| + | of $ {\mathcal R} ^ {m} ( k) $ | ||
| + | such that $ G \circ f = f ^ { \prime } \circ g $. | ||
==Immersion classes.== | ==Immersion classes.== | ||
| − | The geometry of higher-dimensional immersed manifolds arose and developed a long time ago from the theory of the existence of isometric immersions of Riemannian manifolds in | + | The geometry of higher-dimensional immersed manifolds arose and developed a long time ago from the theory of the existence of isometric immersions of Riemannian manifolds in $ \mathbf R ^ {n} $, |
| + | or less often in a space of constant curvature $ K $( | ||
| + | see [[Isometric immersion|Isometric immersion]]). Concerning extrinsic geometrical properties and the links between the extrinsic and the intrinsic geometry of surfaces, two-dimensional surfaces in $ \mathbf R ^ {3} $ | ||
| + | only have been examined in detail. In that case there exists a classification of the points on the surface, leading for two-dimensional surfaces to the classes of convex surfaces, saddle surfaces and developable surfaces. Among others, these classes are basic objects of research in differential geometry in the large. In the higher-dimensional case, no such classification of points on a surface is known (1983). Only certain classes of higher-dimensional surfaces are known: $ k $- | ||
| + | convex, $ k $- | ||
| + | saddle, $ k $- | ||
| + | developable surfaces. | ||
| − | == | + | == $ k $-convex surfaces.== |
| − | A surface | + | A surface $ F ^ { m } $ |
| + | in $ \mathbf R ^ {n} $ | ||
| + | is called $ k $- | ||
| + | convex if for each point $ p \in F ^ { m } $ | ||
| + | there exists a normal $ \xi _ {p} \in ( \nu F ^ { m } ) _ {p} $ | ||
| + | for which $ h _ {p} ( \xi ) $ | ||
| + | is positive definite, and if for any $ k $- | ||
| + | dimensional direction $ \sigma _ {k} \in ( TF ^ { m } ) _ {p} $, | ||
| + | $ 2 \leq k \leq m $, | ||
| + | one can find on $ \sigma _ {k} $ | ||
| + | a two-dimensional direction $ \sigma _ {2} $ | ||
| + | such that $ h _ {p} ( \xi ) ( X, Y) > 0 $( | ||
| + | or $ h _ {p} ( \xi ) ( X, Y) \equiv 0 $) | ||
| + | for each $ \xi _ {p} \in ( \nu F ^ { m } ) _ {p} $ | ||
| + | for $ X, Y \in \sigma _ {2} $, | ||
| + | $ X, Y \neq 0 $. | ||
| + | A two-convex surface $ F ^ { m } $ | ||
| + | in $ \mathbf R ^ {n} $ | ||
| + | is a convex hypersurface in some $ \mathbf R ^ {m+} 1 \subset \mathbf R ^ {n} $[[#References|[4]]]. The intrinsic metric of a $ k $- | ||
| + | convex surface has the following property: At each point $ p $ | ||
| + | and for each $ k $- | ||
| + | dimensional direction $ \sigma _ {k} $ | ||
| + | in the tangent space one can find a two-dimensional direction $ \sigma _ {2} \subset \sigma _ {k} $ | ||
| + | in which the Riemannian curvature is strictly positive. | ||
| − | == | + | == $ k $-saddle surfaces.== |
| − | A surface | + | A surface $ F ^ { m } $ |
| + | in $ \mathbf R ^ {n} $ | ||
| + | is called $ k $- | ||
| + | saddle if for each point $ p $ | ||
| + | and for each normal $ \xi \in ( \nu F ^ { m } ) _ {p} $ | ||
| + | the number of eigen values of $ h _ {p} ( \xi ) $ | ||
| + | of one fixed sign does not exceed $ ( k- 1) $, | ||
| + | $ 2 \leq k\leq m $. | ||
| + | A two-dimensional $ k $- | ||
| + | saddle surface is an ordinary saddle surface in $ \mathbf R ^ {n} $ | ||
| + | from which one cannot cut off the saddle point with a hyperplane. The intrinsic metric of a $ k $- | ||
| + | saddle surface has the following property: At each point $ p $ | ||
| + | for each $ k $- | ||
| + | dimensional direction $ \sigma _ {k} $ | ||
| + | in the tangent space there is a two-dimensional direction $ \sigma _ {2} \subset \sigma _ {k} $ | ||
| + | in which the Riemannian curvature is not positive. If a $ k $- | ||
| + | saddle surface is complete in $ \mathbf R ^ {n} $, | ||
| + | then its homology $ H _ {i} ( F ^ { m } ) = 0 $ | ||
| + | for $ i \geq k $[[#References|[4]]], [[#References|[5]]]. A complete $ m $- | ||
| + | dimensional $ k $- | ||
| + | saddle surface $ F ^ { m } $ | ||
| + | with non-negative Ricci curvature is a cylinder with generator of dimension $ m- k+ 1 $. | ||
| − | == | + | == $ k $-developable ( $ k $-parabolic) surfaces.== |
| − | A surface | + | A surface $ F ^ { m } $ |
| + | in $ \mathbf R ^ {n} $ | ||
| + | is called $ k $- | ||
| + | developable if for each point $ p $ | ||
| + | there exists a $ k $- | ||
| + | dimensional direction $ \sigma _ {k} \subset ( TF ^ { m } ) _ {p} $ | ||
| + | that consists of eigen vectors belonging to the zero eigen value of the second fundamental form with respect to each normal at the given point. The intrinsic metric of a $ k $- | ||
| + | developable surface has the following property: At each point $ p $ | ||
| + | one can find a $ k $- | ||
| + | dimensional subspace $ \sigma _ {k} $ | ||
| + | of the tangent space $ ( TF ^ { m } ) _ {p} $ | ||
| + | such that $ R _ {XY} = 0 $ | ||
| + | for any vector $ X \in \sigma _ {k} $, | ||
| + | where $ Y \in ( TF ^ { m } ) _ {p} $ | ||
| + | is any vector in the tangent space and $ R _ {XY} $ | ||
| + | is the curvature operator. If a $ k $- | ||
| + | developable surface $ F ^ { m } $ | ||
| + | is complete in $ \mathbf R ^ {n} $ | ||
| + | and carries an intrinsic metric of non-positive Ricci curvature, then it is a cylinder with a $ k $- | ||
| + | dimensional generator . | ||
==Free immersions.== | ==Free immersions.== | ||
| − | If the image of | + | If the image of $ H _ {p} ( X, Y) $ |
| + | has maximum possible dimension $ m ( m+ 1)/2 $ | ||
| + | at each point $ p \in F ^ { m } $, | ||
| + | then the immersion is called free. In that case, the first and second derivatives of the radius vector of the immersion $ F ^ { m } $ | ||
| + | form a linearly independent system. In the class of free immersions there exist isometric immersions of dimension $ n > m( m+ 1)/2 + 3m + 5 $, | ||
| + | giving rise to a complete loss of the connection between the intrinsic and the extrinsic geometry. For example, two free isometric immersions of an $ m $- | ||
| + | dimensional manifold $ M ^ {m} $ | ||
| + | in $ \mathbf R ^ {n} $, | ||
| + | $ n > m( m+ 1)/2 + 3m + 5 $, | ||
| + | may be connected by a homotopy consisting of free isometric immersions of $ M ^ {m} $[[#References|[7]]]. | ||
==Immersions with small codimension.== | ==Immersions with small codimension.== | ||
| − | If the codimension | + | If the codimension $ q $ |
| + | of an immersion is small, then it follows from the conditions on the intrinsic metric of the manifold that there must be restrictions on the second fundamental form of the surface. Also, the properties of the second fundamental form enable one to derive topological and extrinsic geometrical properties for the surface. In particular, one obtains non-immersibility theorems. For example, if an $ M ^ {m} $ | ||
| + | with sectional curvature $ K _ \sigma \leq 0 $ | ||
| + | is isometrically immersed in $ \mathbf R ^ {m+} q $ | ||
| + | with $ q > m $, | ||
| + | then $ M ^ {m} $ | ||
| + | is a $ ( q+ 1) $- | ||
| + | saddle surface and its homology (in the case of completeness) $ H _ {k} $ | ||
| + | vanishes for $ k \geq q+ 1 $[[#References|[5]]]. In particular, a compact $ M ^ {m} $ | ||
| + | with $ K _ \sigma \leq 0 $ | ||
| + | cannot be immersed in $ \mathbf R ^ {2m-} 1 $[[#References|[8]]], [[#References|[9]]]. If on the other hand $ K _ \sigma < 0 $, | ||
| + | then $ M ^ {m} $ | ||
| + | is not even locally immersible in $ \mathbf R ^ {2m-} 2 $[[#References|[9]]]. Similarly, an $ M ^ {m} $ | ||
| + | with $ K _ \sigma < 1 $ | ||
| + | is not immersible in the sphere $ S ^ {2m-} 2 $ | ||
| + | of radius 1. A compact $ F ^ { m } $ | ||
| + | in $ S ^ {2m-} 1 $ | ||
| + | has Euler characteristic zero and a compact parallelizable covering manifold if $ K _ \sigma < 1 $[[#References|[10]]]. Regarding a surface $ F ^ { m } $ | ||
| + | in $ \mathbf R ^ {m+} q $ | ||
| + | for $ q \leq m + 2r - 2 $ | ||
| + | and $ K _ \sigma < 0 $, | ||
| + | it is known that its normal Pontryagin classes (cf. [[Pontryagin class|Pontryagin class]]) satisfy the conditions | ||
| − | + | $$ | |
| + | \sum 2 ^ {q-} 2 p _ {i} ^ \perp p _ {r-} i ^ \perp = 0. | ||
| + | $$ | ||
| − | If | + | If $ K _ \sigma > 0 $, |
| + | it follows from $ q \leq m- 1 $ | ||
| + | that $ F ^ { m } $ | ||
| + | is a $ ( q+ 1) $- | ||
| + | convex surface [[#References|[9]]]. In particular, for $ q = 1 $ | ||
| + | it is a two-convex surface. If $ K _ \sigma > 0 $ | ||
| + | and $ q = 2 $, | ||
| + | a compact surface $ F ^ { m } $ | ||
| + | with $ m \geq 3 $ | ||
| + | has the homologies of a sphere [[#References|[11]]]. If $ F ^ { m } $ | ||
| + | in $ \mathbf R ^ {m+} q $ | ||
| + | has non-positive sectional curvature, then it is an $ ( m- q( q+ 1)) $- | ||
| + | developable surface and, in the case of completeness, $ F ^ { m } $ | ||
| + | is a cylinder with generator of dimension $ m- q( q+ 1) $[[#References|[10]]]. If, on the other hand, $ M ^ {m} = M ^ {k} \times \mathbf R ^ {m-} k $ | ||
| + | and $ q \leq n- 2k $, | ||
| + | the immersion of the manifold $ M ^ {m} $ | ||
| + | in $ \mathbf R ^ {m+} q $ | ||
| + | is a $ ( m- 2k- q) $- | ||
| + | developable surface [[#References|[8]]], and in the case of completeness $ F ^ { m } $ | ||
| + | is a cylinder with generator of dimension $ m - 2k - q $. | ||
| + | Under more general assumptions, a compact surface | ||
| − | + | $$ | |
| + | M ^ {m} = M ^ {p _ {1} } \times \dots \times M ^ {p _ {q} } \rightarrow | ||
| + | \mathbf R ^ {n+} q ,\ p _ {i} \geq 2 , | ||
| + | $$ | ||
is a product of hypersurfaces [[#References|[12]]]. | is a product of hypersurfaces [[#References|[12]]]. | ||
| Line 152: | Line 531: | ||
====References==== | ====References==== | ||
<table><TR><TD valign="top">[1]</TD> <TD valign="top"> L.P. Eisenhart, "Riemannian geometry" , Princeton Univ. Press (1949)</TD></TR><TR><TD valign="top">[2]</TD> <TD valign="top"> B.-Y. Chen, "Geometry of submanifolds" , M. Dekker (1973)</TD></TR><TR><TD valign="top">[3]</TD> <TD valign="top"> S.-S. Chern, R.K. Lashof, "On the total curvature of immersed manifolds" ''Amer. J. Math.'' , '''79''' (1957) pp. 306–318</TD></TR><TR><TD valign="top">[4]</TD> <TD valign="top"> S.Z. Shefel', "Two classes of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/g/g044/g044340/g044340328.png" />-dimensional surfaces in <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/g/g044/g044340/g044340329.png" />-dimensional Euclidean space" ''Sib. Math. J.'' , '''10''' (1969) pp. 328–333 ''Sibirsk. Mat. Zh.'' , '''10''' : 2 (1969) pp. 459–466</TD></TR><TR><TD valign="top">[5]</TD> <TD valign="top"> V.V. Glazyrin, "Topological and metric properties of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/g/g044/g044340/g044340330.png" />-saddle surfaces" ''Soviet Math. Dokl.'' , '''18''' (1977) pp. 532–534 ''Dokl. Akad. Nauk SSSR'' , '''233''' : 6 (1977) pp. 1028–1030</TD></TR><TR><TD valign="top">[6a]</TD> <TD valign="top"> P. Hartman, "On isometric immersions in Euclidean space of manifolds with non-negative sectional curvatures" ''Trans. Amer. Math. Soc.'' , '''115''' (1965) pp. 94–109</TD></TR><TR><TD valign="top">[6b]</TD> <TD valign="top"> P. Hartman, "On the isometric immersions in Euclidean space of manifolds with nonnegative sectional curvatures II" ''Trans. Amer. Math. Soc.'' , '''147''' (1970) pp. 529–540</TD></TR><TR><TD valign="top">[7]</TD> <TD valign="top"> M.L. Gromov, "Isometric imbeddings and immersions" ''Soviet Math. Dokl.'' , '''11''' (1970) pp. 794–797 ''Dokl. Akad. Nauk SSSR'' , '''192''' : 6 (1970) pp. 1206–1209</TD></TR><TR><TD valign="top">[8]</TD> <TD valign="top"> S.-S. Chern, N.H. Kuiper, "Some theorems on the isometric imbedding of compact Riemann manifolds in Euclidean space" ''Ann. of Math.'' , '''56''' : 3 (1952) pp. 422–430</TD></TR><TR><TD valign="top">[9]</TD> <TD valign="top"> Yu.E. Borovskii, S.Z. Shefel', "On Chern–Kuiper theorem" ''Sib. Math. J.'' , '''19''' (1978) pp. 978 ''Sibirsk. Mat. Zh.'' , '''19''' : 6 (1978) pp. 1386–1387</TD></TR><TR><TD valign="top">[10]</TD> <TD valign="top"> A.A. Borisenko, "Complete <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/g/g044/g044340/g044340331.png" />-dimensional surfaces of nonpositive extrinsic curvature in a Riemannian space" ''Math. USSR Sb.'' , '''33''' (1977) pp. 485–499 ''Mat. Sb.'' , '''104''' : 4 (1977) pp. 559–576</TD></TR><TR><TD valign="top">[11]</TD> <TD valign="top"> J.D. Moore, "Codimension two submanifolds of positive curvature" ''Proc. Amer. Math. Soc.'' , '''70''' : 1 (1978) pp. 72–74</TD></TR><TR><TD valign="top">[12]</TD> <TD valign="top"> R.B. Gardner, "New viewpoints in the geometry of submanifolds of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/g/g044/g044340/g044340332.png" />" ''Bull. Amer. Math. Soc.'' , '''83''' : 1 (1977) pp. 1–35</TD></TR></table> | <table><TR><TD valign="top">[1]</TD> <TD valign="top"> L.P. Eisenhart, "Riemannian geometry" , Princeton Univ. Press (1949)</TD></TR><TR><TD valign="top">[2]</TD> <TD valign="top"> B.-Y. Chen, "Geometry of submanifolds" , M. Dekker (1973)</TD></TR><TR><TD valign="top">[3]</TD> <TD valign="top"> S.-S. Chern, R.K. Lashof, "On the total curvature of immersed manifolds" ''Amer. J. Math.'' , '''79''' (1957) pp. 306–318</TD></TR><TR><TD valign="top">[4]</TD> <TD valign="top"> S.Z. Shefel', "Two classes of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/g/g044/g044340/g044340328.png" />-dimensional surfaces in <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/g/g044/g044340/g044340329.png" />-dimensional Euclidean space" ''Sib. Math. J.'' , '''10''' (1969) pp. 328–333 ''Sibirsk. Mat. Zh.'' , '''10''' : 2 (1969) pp. 459–466</TD></TR><TR><TD valign="top">[5]</TD> <TD valign="top"> V.V. Glazyrin, "Topological and metric properties of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/g/g044/g044340/g044340330.png" />-saddle surfaces" ''Soviet Math. Dokl.'' , '''18''' (1977) pp. 532–534 ''Dokl. Akad. Nauk SSSR'' , '''233''' : 6 (1977) pp. 1028–1030</TD></TR><TR><TD valign="top">[6a]</TD> <TD valign="top"> P. Hartman, "On isometric immersions in Euclidean space of manifolds with non-negative sectional curvatures" ''Trans. Amer. Math. Soc.'' , '''115''' (1965) pp. 94–109</TD></TR><TR><TD valign="top">[6b]</TD> <TD valign="top"> P. Hartman, "On the isometric immersions in Euclidean space of manifolds with nonnegative sectional curvatures II" ''Trans. Amer. Math. Soc.'' , '''147''' (1970) pp. 529–540</TD></TR><TR><TD valign="top">[7]</TD> <TD valign="top"> M.L. Gromov, "Isometric imbeddings and immersions" ''Soviet Math. Dokl.'' , '''11''' (1970) pp. 794–797 ''Dokl. Akad. Nauk SSSR'' , '''192''' : 6 (1970) pp. 1206–1209</TD></TR><TR><TD valign="top">[8]</TD> <TD valign="top"> S.-S. Chern, N.H. Kuiper, "Some theorems on the isometric imbedding of compact Riemann manifolds in Euclidean space" ''Ann. of Math.'' , '''56''' : 3 (1952) pp. 422–430</TD></TR><TR><TD valign="top">[9]</TD> <TD valign="top"> Yu.E. Borovskii, S.Z. Shefel', "On Chern–Kuiper theorem" ''Sib. Math. J.'' , '''19''' (1978) pp. 978 ''Sibirsk. Mat. Zh.'' , '''19''' : 6 (1978) pp. 1386–1387</TD></TR><TR><TD valign="top">[10]</TD> <TD valign="top"> A.A. Borisenko, "Complete <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/g/g044/g044340/g044340331.png" />-dimensional surfaces of nonpositive extrinsic curvature in a Riemannian space" ''Math. USSR Sb.'' , '''33''' (1977) pp. 485–499 ''Mat. Sb.'' , '''104''' : 4 (1977) pp. 559–576</TD></TR><TR><TD valign="top">[11]</TD> <TD valign="top"> J.D. Moore, "Codimension two submanifolds of positive curvature" ''Proc. Amer. Math. Soc.'' , '''70''' : 1 (1978) pp. 72–74</TD></TR><TR><TD valign="top">[12]</TD> <TD valign="top"> R.B. Gardner, "New viewpoints in the geometry of submanifolds of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/g/g044/g044340/g044340332.png" />" ''Bull. Amer. Math. Soc.'' , '''83''' : 1 (1977) pp. 1–35</TD></TR></table> | ||
| − | |||
| − | |||
====Comments==== | ====Comments==== | ||
| − | The mean curvature is the length of the mean curvature normal which is given by the trace of the bilinear (normal vector-valued) form | + | The mean curvature is the length of the mean curvature normal which is given by the trace of the bilinear (normal vector-valued) form $ H $ |
| + | with respect to the first fundamental form. Minimal immersions are defined by the property that the mean curvature normal vanishes identically. They locally solve the least area problem. | ||
The integrand of the Chern–Lashof curvature is the absolute value of the Lipschitz–Killing curvature. The well-known Chern–Lashof theorem states that the Chern–Lashof curvature is at least 2 for compact immersed submanifolds of Euclidean spaces, and the value 2 is obtained just for convex hyperspheres of affine subspaces of suitable dimensions. | The integrand of the Chern–Lashof curvature is the absolute value of the Lipschitz–Killing curvature. The well-known Chern–Lashof theorem states that the Chern–Lashof curvature is at least 2 for compact immersed submanifolds of Euclidean spaces, and the value 2 is obtained just for convex hyperspheres of affine subspaces of suitable dimensions. | ||
Latest revision as of 19:41, 5 June 2020
A theory that deals with the extrinsic geometry and the relation between the extrinsic and intrinsic geometry (cf. also Interior geometry) of submanifolds in a Euclidean or Riemannian space. The geometry of immersed manifolds is a generalization of the classical differential geometry of surfaces in the Euclidean space $ \mathbf R ^ {3} $.
The intrinsic and extrinsic geometries of an immersed manifold are usually described locally by means of the first and the second fundamental form, respectively. For immersions of an $ m $-
dimensional manifold $ M ^ {m} $
in a manifold $ N ^ {n} $
one has a concept of congruence (see Immersion of a manifold). In the geometry of immersed manifolds one examines properties that are identical for congruent immersions, i.e. properties of a surface $ F ^ { m } $
defined by an immersion $ f $.
In this connection, an immersion and a surface are not distinguished from the geometrical point of view. An immersion $ f $
induces a mapping $ df: TM ^ {m} \rightarrow TN ^ {n} $
of the tangent bundles (cf. Tangent bundle).
The first quadratic (fundamental) form $ g $ of a submanifold $ F $ is defined on $ TM ^ {m} $ by
$$ g _ {p} ( X, Y) = \overline{g}\; _ {f( g) } ( X, Y), $$
where $ p \in M ^ {m} $, $ X, Y \in TM ^ {m} $ and $ \overline{g}\; $ is a Riemannian metric on $ N ^ {n} $. Here and subsequently, the vectors $ X \in TM ^ {m} $ are not distinguished in symbols from their image $ df( X) $. The quadratic form $ g $ defines the structure of a Riemannian space $ M _ {g} ^ {m} $ on $ M ^ {m} $; the properties of $ M _ {g} ^ {m} $ constitute the subject of the intrinsic geometry of the submanifold $ F $. If $ \{ x ^ {k} \} $, $ \{ y ^ \alpha \} $, $ k = 1 \dots m $, $ \alpha = 1 \dots n $, are local coordinates in $ M ^ {m} $ and $ N ^ {n} $, the immersion $ f $ is given by the parametric equations $ y ^ \alpha = f ^ \alpha ( x ^ {1} \dots x ^ {m} ) $. In local coordinates
$$ g _ {p} ( X, Y) = g _ {ij} ( p) X ^ {i} Y ^ {j} , $$
where $ \{ X ^ {i} \} $ and $ \{ Y ^ {j} \} $ are the components of the vectors $ X $ and $ Y $,
$$ g _ {ij} = \overline{g}\; _ {\alpha \beta } \frac{\partial f _ \alpha }{\partial x ^ {i} } \frac{\partial f _ \beta }{\partial x ^ {j} } , $$
and $ \{ \overline{g}\; _ {\alpha \beta } \} $ are the components of the metric tensor $ \overline{g}\; $ of the Riemannian space $ N ^ {n} $.
Concepts such as curve length, volume of a region, Levi-Civita connection $ \nabla _ {X} $ of the intrinsic metric, curvature transformation $ R( X, Y) Z $, etc., relate to the intrinsic geometry of $ F $. The computational formulas applying here can be consulted in Riemannian geometry.
The second (fundamental) tensor (form) $ H $ is defined by
$$ H( X, Y) _ {p} = ( \overline \nabla \; _ {X} Y) _ {p} - (\nabla _ {X} Y) _ {p} , $$
where $ \overline \nabla \; $ and $ \nabla $ are the Levi-Civita connections in $ N ^ {n} $ and $ M ^ {m} $, respectively. In fact, $ H $ is not dependent on the vector fields $ X $ and $ Y $ but only on their values at the point $ p $ and is a bilinear symmetric mapping
$$ ( TM ^ {m} ) _ {p} \times ( TM ^ {m} ) _ {p} \rightarrow ( \nu M ^ {m} ) _ {p} , $$
where $ \nu M ^ {m} $ is the normal bundle of $ M ^ {m} $ in $ N ^ {n} $. For each unit vector $ \xi \in ( \nu M ^ {m} ) _ {p} $, the equations
$$ \langle H ( X, Y), \xi \rangle _ {p} = h _ \xi ( X, Y) _ {p} = \ \langle A _ \xi ( X), Y \rangle _ {p} $$
define the second quadratic form (or second fundamental form) $ h _ \xi $ and the shape operator $ A _ \xi $ in the direction of $ \xi $. In local coordinates the components $ h _ {ij} ( \xi ) $ of the form $ h _ \xi $ are
$$ h _ {ij} ( \xi ) = \ \overline{g}\; _ {\alpha \beta } \frac{\partial ^ {2} f ^ { \alpha } }{\partial x ^ {i} \partial x ^ {j} } \xi ^ \beta , $$
where $ \{ \xi ^ \beta \} $ are the components of $ \xi $.
One defines the principal curvature, principal direction in the direction of $ \xi $, and other related concepts for the form $ h _ \xi $ in the usual way (i.e. as for a surface in the Euclidean space $ \mathbf R ^ {3} $).
Using elementary symmetric functions, one can construct various principal-curvature functions, such as, for example, the mean curvature
$$ H = \frac{1}{m} \sqrt {\sum _ {j= 1 } ^ { {m+ } n } \left ( \sum _ {i= 1 } ^ { m } K _ {i} ( \xi _ {j} ) \right ) ^ {2} } , $$
where $ \{ \xi _ {i} \} $ is an orthonormal set of normals and $ K _ {i} ( \xi ) $ are the principal curvatures of the forms $ h _ {i} $; the Chern–Lashof curvature
$$ K = \frac{1}{\omega _ {n- m- 1 } } \int\limits _ {\xi \in S ^ {n- m- 1 } } | K _ {1} ( \xi ) \dots K _ {m} ( \xi ) | d \sigma , $$
where $ \omega _ {l} $ is the volume of the sphere $ S ^ {l} $; and also the length of the second fundamental form
$$ S = \sqrt {\sum _ { i,j } K _ {i} ^ {2} ( \xi _ {j} ) } $$
The values of the first and second fundamental forms for a submanifold at a point $ p $ define it near $ p $ infinitesimally up to small quantities of the second order. Each $ \xi \in ( \nu M ^ {m} ) _ {p} $, $ | \xi | = 1 $, corresponds to an osculating paraboloid (for a submanifold in a Euclidean space, this is the osculating paraboloid for the projection of the submanifold on the $ ( m+ 1) $- dimensional plane defined by $ ( TM ^ {m} ) _ {p} $ and $ \xi $). If $ m = n- 1 $( i.e. in the case of a hypersurface), the form $ h _ \xi $ is unique up to sign. In that case, the second fundamental tensor and the second fundamental form do not differ, and the theory acquires considerable similarity with the classical theory of surfaces in $ \mathbf R ^ {3} $.
Basic equations.
The basic equations for an immersed manifold, i.e. the Gauss equations, the Codazzi–Mainardi equations and the Ricci equations, relate the first and second fundamental forms and the curvature tensors of $ M $ and $ N $. For each vector field section $ X $ over $ M $ of the vector bundle $ TN $ restricted to $ M $, let $ t ( X) $ denote the tangential component and $ n ( X) $ the normal component. The Gauss formula defining the second fundamental form,
$$ \overline \nabla \; _ {X} Y = \nabla _ {X} Y + H ( X , Y ), $$
gives the normal-tangent decomposition of $ \overline \nabla \; _ {X} Y $ for $ X , Y $ vector fields on $ M $. The Weingarten formula (defining the shape operator),
$$ \overline \nabla \; _ {X} \xi = - A _ \xi X + D _ {X} \xi , $$
does the same in case $ X $ is a vector field on $ M $ and the section $ \xi $ of $ TN $ is normal to $ M $. In terms of the shape operators and the second fundamental form one finds that for three vector fields $ X $, $ Y $, $ Z $ on $ M $ the tangential component of $ \overline{R}\; ( X , Y ) Z $ is equal to
$$ t ( \overline{R}\; ( X , Y ) Z ) = \ R ( X , Y ) Z + A _ {H ( X , Z ) } ( Y) - A _ {H ( Y , Z ) } ( X) . $$
Taking a fourth vector field $ W $ on $ M $ this leads to the Gauss equations
$$ \tag{1 } \langle \overline{R}\; ( X , Y ) Z , W \rangle = $$
$$ = \ \langle R ( X , Y ) Z , W \rangle + $$
$$ + \langle H ( X , Z ) , H ( Y , W ) \rangle - \langle H ( Y , Z ) , H ( X , W ) \rangle . $$
The normal component of $ \overline{R}\; ( X , Y ) Z $ is equal to
$$ \tag{2 } n ( \overline{R}\; ( X , Y ) Z ) = $$
$$ = \ D _ {X} H ( Y , Z ) - D _ {Y} H ( X , Z ) + $$
$$ + H ( X , \nabla _ {Y} Z ) - H ( Y , \nabla _ {X} Z ) - H ( [ X , Y ] , Z ) . $$
Define the connection $ \widetilde \nabla $ on the vector bundle $ \mathop{\rm Hom} ( TM \times TM , \nu ( M) ) $, where $ \nu ( M) $ is the normal bundle to $ M $ in $ N $, by the formula
$$ ( \widetilde \nabla _ {X} s ) ( Y , Z ) = \ D _ {X} ( s ( Y , Z ) ) - s ( \nabla _ {X} Y , Z ) - s ( Y , \nabla _ {X} Z ) . $$
Then (2) can be rewritten as
$$ \tag{2'} n ( \overline{R}\; ( X , Y ) Z ) = \ ( \widetilde \nabla _ {X} H ) ( Y , Z ) - ( \widetilde \nabla _ {Y} H ) ( X , Z ) . $$
Equations (2) (or (2'})) are the Codazzi–Mainardi equations (in intrinsic form) (cf. also Peterson–Codazzi equations).
Finally, consider the normal component of $ \overline{R}\; ( X , Y ) \xi $ where $ \xi $ is a section of $ \nu ( M) $( by the symmetry properties of $ \overline{R}\; ( W , \xi , X , Y ) = \langle R ( X , Y ) \xi , W \rangle $ the horizontal component follows from the Codazzi–Mainardi equations). One has
$$ \tag{3 } n ( \overline{R}\; ( X , Y ) \xi ) = \ \widetilde{R} ( X , Y ) \xi - H ( X , A _ \xi Y ) + H ( Y , A _ \xi X ) , $$
the Ricci equations. Here $ \widetilde{R} = R _ {D} $ is the curvature tensor of the connection $ D $ on the normal bundle $ \nu ( M) $. The Gauss, Codazzi–Mainardi and Ricci equations are the only general equations available for an isometric immersion. It is reasonable to expect something interesting for $ R ( \cdot , \cdot , \cdot , \cdot ) $ if three of the fields are normal. Indeed, $ ( R ( \xi , \eta ) \xi ) _ {P} $ then has nothing to do with the immersed manifold $ M $ at the point $ P $( except with the point $ P $ itself).
If the ambient manifold $ N $ is of constant curvature $ k $, then $ \overline{R}\; ( X , Y ) Z = k ( \langle Z , Y \rangle X - \langle Z , X \rangle Y ) $ and so $ \overline{R}\; ( X , Y ) Z $ is tangent to $ M $. The Gauss, Ricci and Codazzi–Mainardi equations reduce to
$$ \tag{4 } \langle R ( X , Y ) Z , W \rangle = $$
$$ = \ k ( \langle X , W > < Y , Z > - < X , Z \rangle \langle Y , W \rangle ) + $$
$$ + \langle H ( X , W ) , H ( Y , Z ) \rangle - \langle H ( X , Z ) , H ( Y , W ) \rangle , $$
$$ \tag{5 } \langle \overline{R}\; ( X , Y ) \xi , \eta \rangle = < \widetilde{R} ( X , Y ) \xi , \eta > + \langle [ A _ \xi , A _ \eta ] X , Y \rangle , $$
where $ [ A _ \xi , A _ \eta ] = A _ \xi A _ \eta - A _ \eta A _ \xi $, and
$$ \tag{6 } \widetilde \Delta _ {X} H ( Y , Z ) - \widetilde \Delta _ {Y} H ( X , Z ) = 0 . $$
These equations make sense in a more general setting. Indeed, let $ E $ be a Riemannian vector bundle over $ M $, i.e. there is a (bundle) Riemannian metric $ \langle \cdot , \cdot \rangle _ {E} $ on $ E $, and let there be a Riemannian connection $ D : TM \times \Gamma ( E) \rightarrow E $, where $ \Gamma ( E) $ denotes the space of smooth sections of $ E $, which is adapted to the metric. This last phrase means that $ \nabla _ {X} \langle \xi , \eta > = < D _ {X} \xi , \eta \rangle + \langle \xi , D _ {X} \eta \rangle $. A bilinear mapping $ A : TM \times E \rightarrow TM $ such that $ A _ \xi : TM \rightarrow TM $ is self-adjoint for all $ \xi $ is called a second fundamental tensor in $ E $. The associated second fundamental form in $ E $ is then defined by
$$ \langle H ( X , Y ) , \xi \rangle _ {E} = \langle A _ \xi X , Y \rangle . $$
The three equations (4), (5), (6) make perfect sense in this more general setting. One has now the following generalization of the Bonnet theorem [2]: Let $ M $ be a simply-connected Riemannian manifold equipped with a Riemannian vector bundle of dimension $ n $ with a compatible connection $ D $, second fundamental tensor $ A $ and associated second fundamental form $ H $. Suppose that equations (4), (5), (6) hold. Then there is an isometric immersion of $ M $ into a simply-connected Riemannian manifold of constant curvature $ k $( a space form) and dimension $ \mathop{\rm dim} ( M) + n $ such that the normal bundle is $ E $.
This immersion is unique in the following sense. Let $ f , f ^ { \prime } : M \rightarrow {\mathcal R} ^ {m} ( k) $ be two isometric immersions of $ M $ into a space form $ {\mathcal R} ^ {m} ( k) $ of curvature $ k $ and with normal bundles $ E $ and $ E ^ \prime $, with their induced bundle metrics, second fundamental forms and connections. Suppose that there is a bundle mapping $ E \rightarrow E ^ \prime $,
$$ \begin{array}{lcl} E & \mathop \rightarrow \limits ^ \alpha &E ^ \prime \\ \downarrow &{} &\downarrow \\ M & \rightarrow _ { g } & M \\ \end{array} $$
covering an isometry $ g $ of $ M $ and such that $ \alpha $ preserves the bundle metrics, connections and second fundamental forms. Then there is a rigid motion $ G $ of $ {\mathcal R} ^ {m} ( k) $ such that $ G \circ f = f ^ { \prime } \circ g $.
Immersion classes.
The geometry of higher-dimensional immersed manifolds arose and developed a long time ago from the theory of the existence of isometric immersions of Riemannian manifolds in $ \mathbf R ^ {n} $, or less often in a space of constant curvature $ K $( see Isometric immersion). Concerning extrinsic geometrical properties and the links between the extrinsic and the intrinsic geometry of surfaces, two-dimensional surfaces in $ \mathbf R ^ {3} $ only have been examined in detail. In that case there exists a classification of the points on the surface, leading for two-dimensional surfaces to the classes of convex surfaces, saddle surfaces and developable surfaces. Among others, these classes are basic objects of research in differential geometry in the large. In the higher-dimensional case, no such classification of points on a surface is known (1983). Only certain classes of higher-dimensional surfaces are known: $ k $- convex, $ k $- saddle, $ k $- developable surfaces.
$ k $-convex surfaces.
A surface $ F ^ { m } $ in $ \mathbf R ^ {n} $ is called $ k $- convex if for each point $ p \in F ^ { m } $ there exists a normal $ \xi _ {p} \in ( \nu F ^ { m } ) _ {p} $ for which $ h _ {p} ( \xi ) $ is positive definite, and if for any $ k $- dimensional direction $ \sigma _ {k} \in ( TF ^ { m } ) _ {p} $, $ 2 \leq k \leq m $, one can find on $ \sigma _ {k} $ a two-dimensional direction $ \sigma _ {2} $ such that $ h _ {p} ( \xi ) ( X, Y) > 0 $( or $ h _ {p} ( \xi ) ( X, Y) \equiv 0 $) for each $ \xi _ {p} \in ( \nu F ^ { m } ) _ {p} $ for $ X, Y \in \sigma _ {2} $, $ X, Y \neq 0 $. A two-convex surface $ F ^ { m } $ in $ \mathbf R ^ {n} $ is a convex hypersurface in some $ \mathbf R ^ {m+} 1 \subset \mathbf R ^ {n} $[4]. The intrinsic metric of a $ k $- convex surface has the following property: At each point $ p $ and for each $ k $- dimensional direction $ \sigma _ {k} $ in the tangent space one can find a two-dimensional direction $ \sigma _ {2} \subset \sigma _ {k} $ in which the Riemannian curvature is strictly positive.
$ k $-saddle surfaces.
A surface $ F ^ { m } $ in $ \mathbf R ^ {n} $ is called $ k $- saddle if for each point $ p $ and for each normal $ \xi \in ( \nu F ^ { m } ) _ {p} $ the number of eigen values of $ h _ {p} ( \xi ) $ of one fixed sign does not exceed $ ( k- 1) $, $ 2 \leq k\leq m $. A two-dimensional $ k $- saddle surface is an ordinary saddle surface in $ \mathbf R ^ {n} $ from which one cannot cut off the saddle point with a hyperplane. The intrinsic metric of a $ k $- saddle surface has the following property: At each point $ p $ for each $ k $- dimensional direction $ \sigma _ {k} $ in the tangent space there is a two-dimensional direction $ \sigma _ {2} \subset \sigma _ {k} $ in which the Riemannian curvature is not positive. If a $ k $- saddle surface is complete in $ \mathbf R ^ {n} $, then its homology $ H _ {i} ( F ^ { m } ) = 0 $ for $ i \geq k $[4], [5]. A complete $ m $- dimensional $ k $- saddle surface $ F ^ { m } $ with non-negative Ricci curvature is a cylinder with generator of dimension $ m- k+ 1 $.
$ k $-developable ( $ k $-parabolic) surfaces.
A surface $ F ^ { m } $ in $ \mathbf R ^ {n} $ is called $ k $- developable if for each point $ p $ there exists a $ k $- dimensional direction $ \sigma _ {k} \subset ( TF ^ { m } ) _ {p} $ that consists of eigen vectors belonging to the zero eigen value of the second fundamental form with respect to each normal at the given point. The intrinsic metric of a $ k $- developable surface has the following property: At each point $ p $ one can find a $ k $- dimensional subspace $ \sigma _ {k} $ of the tangent space $ ( TF ^ { m } ) _ {p} $ such that $ R _ {XY} = 0 $ for any vector $ X \in \sigma _ {k} $, where $ Y \in ( TF ^ { m } ) _ {p} $ is any vector in the tangent space and $ R _ {XY} $ is the curvature operator. If a $ k $- developable surface $ F ^ { m } $ is complete in $ \mathbf R ^ {n} $ and carries an intrinsic metric of non-positive Ricci curvature, then it is a cylinder with a $ k $- dimensional generator .
Free immersions.
If the image of $ H _ {p} ( X, Y) $ has maximum possible dimension $ m ( m+ 1)/2 $ at each point $ p \in F ^ { m } $, then the immersion is called free. In that case, the first and second derivatives of the radius vector of the immersion $ F ^ { m } $ form a linearly independent system. In the class of free immersions there exist isometric immersions of dimension $ n > m( m+ 1)/2 + 3m + 5 $, giving rise to a complete loss of the connection between the intrinsic and the extrinsic geometry. For example, two free isometric immersions of an $ m $- dimensional manifold $ M ^ {m} $ in $ \mathbf R ^ {n} $, $ n > m( m+ 1)/2 + 3m + 5 $, may be connected by a homotopy consisting of free isometric immersions of $ M ^ {m} $[7].
Immersions with small codimension.
If the codimension $ q $ of an immersion is small, then it follows from the conditions on the intrinsic metric of the manifold that there must be restrictions on the second fundamental form of the surface. Also, the properties of the second fundamental form enable one to derive topological and extrinsic geometrical properties for the surface. In particular, one obtains non-immersibility theorems. For example, if an $ M ^ {m} $ with sectional curvature $ K _ \sigma \leq 0 $ is isometrically immersed in $ \mathbf R ^ {m+} q $ with $ q > m $, then $ M ^ {m} $ is a $ ( q+ 1) $- saddle surface and its homology (in the case of completeness) $ H _ {k} $ vanishes for $ k \geq q+ 1 $[5]. In particular, a compact $ M ^ {m} $ with $ K _ \sigma \leq 0 $ cannot be immersed in $ \mathbf R ^ {2m-} 1 $[8], [9]. If on the other hand $ K _ \sigma < 0 $, then $ M ^ {m} $ is not even locally immersible in $ \mathbf R ^ {2m-} 2 $[9]. Similarly, an $ M ^ {m} $ with $ K _ \sigma < 1 $ is not immersible in the sphere $ S ^ {2m-} 2 $ of radius 1. A compact $ F ^ { m } $ in $ S ^ {2m-} 1 $ has Euler characteristic zero and a compact parallelizable covering manifold if $ K _ \sigma < 1 $[10]. Regarding a surface $ F ^ { m } $ in $ \mathbf R ^ {m+} q $ for $ q \leq m + 2r - 2 $ and $ K _ \sigma < 0 $, it is known that its normal Pontryagin classes (cf. Pontryagin class) satisfy the conditions
$$ \sum 2 ^ {q-} 2 p _ {i} ^ \perp p _ {r-} i ^ \perp = 0. $$
If $ K _ \sigma > 0 $, it follows from $ q \leq m- 1 $ that $ F ^ { m } $ is a $ ( q+ 1) $- convex surface [9]. In particular, for $ q = 1 $ it is a two-convex surface. If $ K _ \sigma > 0 $ and $ q = 2 $, a compact surface $ F ^ { m } $ with $ m \geq 3 $ has the homologies of a sphere [11]. If $ F ^ { m } $ in $ \mathbf R ^ {m+} q $ has non-positive sectional curvature, then it is an $ ( m- q( q+ 1)) $- developable surface and, in the case of completeness, $ F ^ { m } $ is a cylinder with generator of dimension $ m- q( q+ 1) $[10]. If, on the other hand, $ M ^ {m} = M ^ {k} \times \mathbf R ^ {m-} k $ and $ q \leq n- 2k $, the immersion of the manifold $ M ^ {m} $ in $ \mathbf R ^ {m+} q $ is a $ ( m- 2k- q) $- developable surface [8], and in the case of completeness $ F ^ { m } $ is a cylinder with generator of dimension $ m - 2k - q $. Under more general assumptions, a compact surface
$$ M ^ {m} = M ^ {p _ {1} } \times \dots \times M ^ {p _ {q} } \rightarrow \mathbf R ^ {n+} q ,\ p _ {i} \geq 2 , $$
is a product of hypersurfaces [12].
References
| [1] | L.P. Eisenhart, "Riemannian geometry" , Princeton Univ. Press (1949) |
| [2] | B.-Y. Chen, "Geometry of submanifolds" , M. Dekker (1973) |
| [3] | S.-S. Chern, R.K. Lashof, "On the total curvature of immersed manifolds" Amer. J. Math. , 79 (1957) pp. 306–318 |
| [4] | S.Z. Shefel', "Two classes of 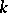 -dimensional surfaces in -dimensional surfaces in  -dimensional Euclidean space" Sib. Math. J. , 10 (1969) pp. 328–333 Sibirsk. Mat. Zh. , 10 : 2 (1969) pp. 459–466 -dimensional Euclidean space" Sib. Math. J. , 10 (1969) pp. 328–333 Sibirsk. Mat. Zh. , 10 : 2 (1969) pp. 459–466 |
| [5] | V.V. Glazyrin, "Topological and metric properties of 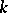 -saddle surfaces" Soviet Math. Dokl. , 18 (1977) pp. 532–534 Dokl. Akad. Nauk SSSR , 233 : 6 (1977) pp. 1028–1030 -saddle surfaces" Soviet Math. Dokl. , 18 (1977) pp. 532–534 Dokl. Akad. Nauk SSSR , 233 : 6 (1977) pp. 1028–1030 |
| [6a] | P. Hartman, "On isometric immersions in Euclidean space of manifolds with non-negative sectional curvatures" Trans. Amer. Math. Soc. , 115 (1965) pp. 94–109 |
| [6b] | P. Hartman, "On the isometric immersions in Euclidean space of manifolds with nonnegative sectional curvatures II" Trans. Amer. Math. Soc. , 147 (1970) pp. 529–540 |
| [7] | M.L. Gromov, "Isometric imbeddings and immersions" Soviet Math. Dokl. , 11 (1970) pp. 794–797 Dokl. Akad. Nauk SSSR , 192 : 6 (1970) pp. 1206–1209 |
| [8] | S.-S. Chern, N.H. Kuiper, "Some theorems on the isometric imbedding of compact Riemann manifolds in Euclidean space" Ann. of Math. , 56 : 3 (1952) pp. 422–430 |
| [9] | Yu.E. Borovskii, S.Z. Shefel', "On Chern–Kuiper theorem" Sib. Math. J. , 19 (1978) pp. 978 Sibirsk. Mat. Zh. , 19 : 6 (1978) pp. 1386–1387 |
| [10] | A.A. Borisenko, "Complete 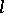 -dimensional surfaces of nonpositive extrinsic curvature in a Riemannian space" Math. USSR Sb. , 33 (1977) pp. 485–499 Mat. Sb. , 104 : 4 (1977) pp. 559–576 -dimensional surfaces of nonpositive extrinsic curvature in a Riemannian space" Math. USSR Sb. , 33 (1977) pp. 485–499 Mat. Sb. , 104 : 4 (1977) pp. 559–576 |
| [11] | J.D. Moore, "Codimension two submanifolds of positive curvature" Proc. Amer. Math. Soc. , 70 : 1 (1978) pp. 72–74 |
| [12] | R.B. Gardner, "New viewpoints in the geometry of submanifolds of 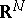 " Bull. Amer. Math. Soc. , 83 : 1 (1977) pp. 1–35 " Bull. Amer. Math. Soc. , 83 : 1 (1977) pp. 1–35 |
Comments
The mean curvature is the length of the mean curvature normal which is given by the trace of the bilinear (normal vector-valued) form $ H $ with respect to the first fundamental form. Minimal immersions are defined by the property that the mean curvature normal vanishes identically. They locally solve the least area problem.
The integrand of the Chern–Lashof curvature is the absolute value of the Lipschitz–Killing curvature. The well-known Chern–Lashof theorem states that the Chern–Lashof curvature is at least 2 for compact immersed submanifolds of Euclidean spaces, and the value 2 is obtained just for convex hyperspheres of affine subspaces of suitable dimensions.
References
| [a1] | M. Gromov, "Partial differential relations" , Springer (1986) (Translated from Russian) |
| [a2] | M. Gromov, V. Rokhlin, "Embeddings and immersions in Riemannian geometry" Russian Math. Surveys , 25 : 5 (1970) pp. 1–57 Uspekhi Mat. Nauk , 25 : 5 (1970) pp. 3–62 |
Geometry of immersed manifolds. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Geometry_of_immersed_manifolds&oldid=47093