Difference between revisions of "Stanley-Reisner ring"
(TeX partly done) |
(TeX partly done) |
||
| Line 15: | Line 15: | ||
$$ | $$ | ||
| − | One may thus | + | One may thus define $I_\Delta$ more compactly as $I_\Delta = \left\langle{ x^F : F \not\in \Delta }\right\rangle$. |
| − | It is easy to verify that the Krull dimension of | + | It is easy to verify that the Krull dimension of $k[\Delta]$ (cf. also [[Dimension]]) is one greater than the dimension of $\Delta$ ($\dim k[\Delta] = (\dim \Delta) + 1$). |
| − | Recall that the Hilbert series of a finitely-generated | + | Recall that the ''Hilbert series'' of a finitely-generated $\mathbf{Z}$-graded module $M$ over a finitely-generated $k$-algebra is defined by |
| + | $$ | ||
| + | F(M,\lambda) = \sum_{i\in\mathbf{Z}} \dim_k M_i \, \lambda^i | ||
| + | $$ | ||
| + | The Hilbert series of $k[\Delta]$ may be described from the combinatorics of $\Delta$. Let <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s130/s130520/s13052029.png" />, let <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s130/s130520/s13052030.png" />, and call <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s130/s130520/s13052031.png" /> the <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s130/s130520/s13052033.png" />-vector of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s130/s130520/s13052034.png" />. Then | ||
<table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s130/s130520/s13052035.png" /></td> </tr></table> | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s130/s130520/s13052035.png" /></td> </tr></table> | ||
Revision as of 20:03, 23 January 2018
Stanley–Reisner face ring, face ring
The Stanley–Reisner ring of a simplicial complex $\Delta$ over a field $k$ is the quotient ring $$ k[\Delta] = k[x_1,\ldots,x_n]/I_\Delta $$ where $\{x_1,\ldots,x_n\}$ are the vertices of $\Delta$, $k[x_1,\ldots,x_n]$ denotes the polynomial ring over $k$ in the variables $\{x_1,\ldots,x_n\}$, and $I_\Delta$ is the ideal in $k[x_1,\ldots,x_n]$ generated by the non-faces of $\Delta$, i.e., $$ I_\Delta = \left\langle{ x_{i_1}\cdots x_{i_j} : \{i_1,\ldots,i_j\} \not\in \Delta }\right\rangle \ . $$
The support of any monomial in $k[\Delta]$ is a face of $\Delta$. In particular, the square-free monomials of $k[\Delta]$ correspond bijectively to the faces of $\Delta$, and are therefore called the face-monomials $$ x^F = \prod_{x_i\in F} x_i \ . $$
One may thus define $I_\Delta$ more compactly as $I_\Delta = \left\langle{ x^F : F \not\in \Delta }\right\rangle$.
It is easy to verify that the Krull dimension of $k[\Delta]$ (cf. also Dimension) is one greater than the dimension of $\Delta$ ($\dim k[\Delta] = (\dim \Delta) + 1$).
Recall that the Hilbert series of a finitely-generated $\mathbf{Z}$-graded module $M$ over a finitely-generated $k$-algebra is defined by
$$
F(M,\lambda) = \sum_{i\in\mathbf{Z}} \dim_k M_i \, \lambda^i
$$
The Hilbert series of $k[\Delta]$ may be described from the combinatorics of $\Delta$. Let 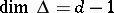 , let
, let  , and call
, and call 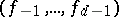 the
the 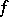 -vector of
-vector of 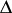 . Then
. Then
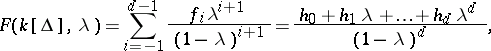 |
where the sequence  , called the
, called the  -vector of
-vector of  , may be derived from the
, may be derived from the 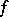 -vector of
-vector of 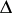 (and vice versa) by the equation
(and vice versa) by the equation
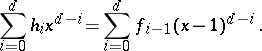 |
The mapping from 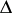 to
to 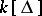 allows properties defined for rings to be naturally extended to simplicial complexes. The most well-known and useful example is Cohen–Macaulayness: A simplicial complex
allows properties defined for rings to be naturally extended to simplicial complexes. The most well-known and useful example is Cohen–Macaulayness: A simplicial complex  is defined to be Cohen–Macaulay (over the field
is defined to be Cohen–Macaulay (over the field 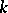 ) when
) when 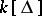 is Cohen–Macaulay (cf. also Cohen–Macaulay ring). The utility of this extension is demonstrated in the proof that if (the geometric realization of) a simplicial complex is homeomorphic to a sphere, then its
is Cohen–Macaulay (cf. also Cohen–Macaulay ring). The utility of this extension is demonstrated in the proof that if (the geometric realization of) a simplicial complex is homeomorphic to a sphere, then its 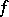 -vector satisfies a condition called the upper bound conjecture (for details, see [a1], Sect. II.3,4). The statement of this result requires no algebra, but the proof relies heavily upon the Stanley–Reisner ring and Cohen–Macaulayness. Many other applications of the Stanley–Reisner ring may be found in [a1], Chaps. II, III.
-vector satisfies a condition called the upper bound conjecture (for details, see [a1], Sect. II.3,4). The statement of this result requires no algebra, but the proof relies heavily upon the Stanley–Reisner ring and Cohen–Macaulayness. Many other applications of the Stanley–Reisner ring may be found in [a1], Chaps. II, III.
Finally, there is an anti-commutative version of the Stanley–Reisner ring, called the exterior face ring or indicator algebra, in which the polynomial ring 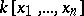 in the definition of
in the definition of 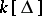 is replaced by the exterior algebra
is replaced by the exterior algebra 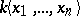 .
.
References
| [a1] | Richard P. Stanley, "Combinatorics and commutative algebra" , (2nd ed.) Birkhäuser (1996) ISBN 0-81764-369-9 Zbl 1157.13302 Zbl 0838.13008 |
Stanley-Reisner ring. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Stanley-Reisner_ring&oldid=42780