Difference between revisions of "Wild knot"
From Encyclopedia of Mathematics
(TeX) |
(picture remake) |
||
| Line 2: | Line 2: | ||
A knot $L$ in the Euclidean space $E^3$ (cf. [[Knot theory|Knot theory]]) such that there is no homeomorphism of $E^3$ onto itself under which $L$ would become a closed polygonal line consisting of a finite number of segments. | A knot $L$ in the Euclidean space $E^3$ (cf. [[Knot theory|Knot theory]]) such that there is no homeomorphism of $E^3$ onto itself under which $L$ would become a closed polygonal line consisting of a finite number of segments. | ||
| − | < | + | <center><asy> |
| + | settings.render = 0; | ||
| − | + | unitsize(100); | |
| + | |||
| + | import three; | ||
| + | import tube; | ||
| + | |||
| + | import graph; | ||
| + | path unitCircle = Circle((0,0),1,35); | ||
| + | |||
| + | currentprojection = perspective((900,-350,-650)); | ||
| + | currentlight=light(gray(0.4),specularfactor=3,viewport=false,(-0.5,-0.5,-0.75),(0,-0.5,0.5),(0.5,0.5,0.75)); | ||
| + | // currentlight=light(gray(0.4),specularfactor=3,viewport=false,(-0.5,-0.5,-0.75),(0.5,-0.5,0.5),(0.5,0.5,0.75)); | ||
| + | |||
| + | triple horn_start=(0,-1,0.6); | ||
| + | triple horn_end=(0,0.4,0.2); | ||
| + | real horn_radius=0.2; | ||
| + | |||
| + | real ratio=horn_end.z/(-horn_start.y); // fractal levels ratio | ||
| + | |||
| + | transform3 implode_right = shift(horn_end) * scale3(ratio) * rotate(-90,X) * shift(-horn_start.y*Y); | ||
| + | transform3 left_right = reflect(O,X,Z)*rotate(90,Y); | ||
| + | |||
| + | path[] cover_with_holes = scale(horn_radius/ratio)*unitCircle^^ | ||
| + | shift((horn_start.z,0))*scale(0.9horn_radius)*reverse(unitCircle)^^ | ||
| + | shift((-horn_start.z,0))*scale(0.9horn_radius)*reverse(unitCircle); | ||
| + | surface cover = surface(cover_with_holes,ZXplane); | ||
| + | surface cover_left = shift((horn_start.x,horn_start.y,0))*cover; | ||
| + | surface two_covers = surface(cover_left,left_right*cover_left); | ||
| + | |||
| + | path3 horn_axis = horn_start..horn_start+(0,0.01,0)..(0,0,0.7)..(0,0.2,0.6)..horn_end+(0,0,0.01)..horn_end; | ||
| + | |||
| + | surface horn = tube( horn_axis, scale(horn_radius)*unitCircle ); | ||
| + | surface two_horns = surface(horn,reflect(O,X,Y)*horn); | ||
| + | surface two_horns = surface(horn,reflect(O,X,Y)*horn); | ||
| + | surface four_horns = surface(two_horns,left_right*two_horns,two_covers); | ||
| + | |||
| + | surface four_small_horns = implode_right*four_horns; | ||
| + | surface eight_small_horns = surface(four_small_horns,left_right*four_small_horns); | ||
| + | |||
| + | surface big_surface = surface(four_horns,eight_small_horns); | ||
| + | |||
| + | real R = horn_radius/ratio; | ||
| + | |||
| + | draw ( circle((0,1,0), 1.005R, Y ), currentpen+2 ); | ||
| + | draw ( circle((horn_start.z,1.01,horn_start.x), horn_radius, Y ), currentpen+2 ); | ||
| + | draw ( circle((-horn_start.z,1.01,horn_start.x), horn_radius, Y ), currentpen+2 ); | ||
| + | |||
| + | draw (big_surface, yellow); | ||
| + | |||
| + | pen blackpen = currentpen+1.5; | ||
| + | |||
| + | draw ( circle((0,-1,0), 1.005R, Y ), blackpen ); | ||
| + | draw ( circle(horn_start, 0.98horn_radius, Y ), blackpen ); | ||
| + | draw ( circle((horn_start.x,horn_start.y,-horn_start.z), 0.98horn_radius, Y ), blackpen ); | ||
| + | |||
| + | real phi=0.9; // adjust to the projection | ||
| + | triple u = (cos(phi),0,sin(phi)); | ||
| + | draw( R*u-Y -- R*u+Y, blackpen ); | ||
| + | draw( -R*u-Y -- -R*u+Y, blackpen ); | ||
| + | |||
| + | </asy></center> | ||
Thus, knots containing the so-called Fox–Artin arcs — certain simple arcs obtained by a [[Wild imbedding|wild imbedding]] in $E^3$ — are wild. For example, the fundamental group $\pi_1(E^3\setminus L)$ is non-trivial for the arc $L_1$ (Fig. a); this group is trivial for the arc $L_2$ (Fig. b), but $E^3\setminus L_2$ itself is not homeomorphic to the complement of a point in $E^3$. | Thus, knots containing the so-called Fox–Artin arcs — certain simple arcs obtained by a [[Wild imbedding|wild imbedding]] in $E^3$ — are wild. For example, the fundamental group $\pi_1(E^3\setminus L)$ is non-trivial for the arc $L_1$ (Fig. a); this group is trivial for the arc $L_2$ (Fig. b), but $E^3\setminus L_2$ itself is not homeomorphic to the complement of a point in $E^3$. | ||
Revision as of 18:56, 12 December 2014
A knot $L$ in the Euclidean space $E^3$ (cf. Knot theory) such that there is no homeomorphism of $E^3$ onto itself under which $L$ would become a closed polygonal line consisting of a finite number of segments.

Thus, knots containing the so-called Fox–Artin arcs — certain simple arcs obtained by a wild imbedding in $E^3$ — are wild. For example, the fundamental group $\pi_1(E^3\setminus L)$ is non-trivial for the arc $L_1$ (Fig. a); this group is trivial for the arc $L_2$ (Fig. b), but $E^3\setminus L_2$ itself is not homeomorphic to the complement of a point in $E^3$.
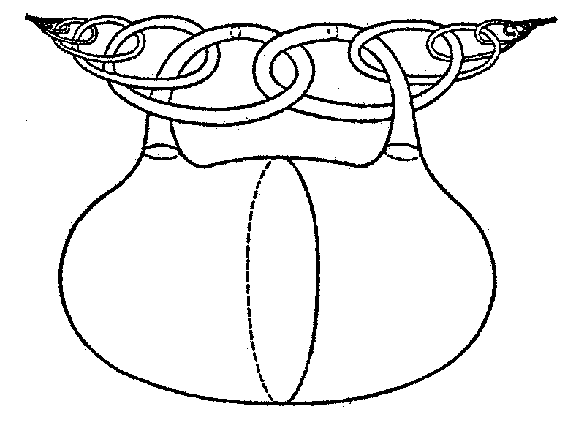
Figure: w097980b
For references see Wild sphere.
How to Cite This Entry:
Wild knot. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Wild_knot&oldid=35580
Wild knot. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Wild_knot&oldid=35580
This article was adapted from an original article by M.I. Voitsekhovskii (originator), which appeared in Encyclopedia of Mathematics - ISBN 1402006098. See original article