Difference between revisions of "Elliptic integral"
m (hyperlink) |
(MSC 33E05) |
||
| Line 1: | Line 1: | ||
| − | An integral of an [[ | + | {{MSC|33E05}} |
| + | |||
| + | An integral of an [[algebraic function]] of the first kind, that is, an integral of the form | ||
<table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/e/e035/e035490/e0354901.png" /></td> <td valign="top" style="width:5%;text-align:right;">(1)</td></tr></table> | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/e/e035/e035490/e0354901.png" /></td> <td valign="top" style="width:5%;text-align:right;">(1)</td></tr></table> | ||
Revision as of 22:08, 28 November 2014
2020 Mathematics Subject Classification: Primary: 33E05 [MSN][ZBL]
An integral of an algebraic function of the first kind, that is, an integral of the form
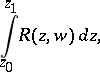 | (1) |
where 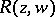 is a rational function of the variables
is a rational function of the variables  and
and 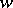 . These variables are connected by an equation
. These variables are connected by an equation
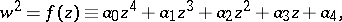 | (2) |
in which 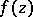 is a polynomial of degree 3 or 4 without multiple roots. Here it is usually understood that the integral (1) cannot be expressed in terms of only one elementary function. When such an expression is possible, then (1) is said to be a pseudo-elliptic integral.
is a polynomial of degree 3 or 4 without multiple roots. Here it is usually understood that the integral (1) cannot be expressed in terms of only one elementary function. When such an expression is possible, then (1) is said to be a pseudo-elliptic integral.
The name elliptic integral stems from the fact that they appeared first in the rectification of the arc of an ellipse and other second-order curves in work by Jacob and Johann Bernoulli, G.C. Fagnano dei Toschi, and L. Euler, who at the end of the 17th century and the beginning of the 18th century laid the foundations of the theory of elliptic integrals and elliptic functions (cf. Elliptic function), which arise in the inversion of elliptic integrals (cf. Inversion of an elliptic integral).
To the equations (2) corresponds a two-sheeted compact Riemann surface 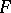 of genus
of genus 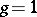 , homeomorphic to a torus, on which
, homeomorphic to a torus, on which  and
and 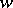 , and hence also
, and hence also 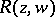 , regarded as functions of a point of
, regarded as functions of a point of 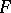 , are single-valued. The integral (1) is given as the integral
, are single-valued. The integral (1) is given as the integral 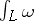 of the Abelian differential
of the Abelian differential 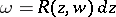 on
on 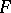 , taken along some rectifiable path
, taken along some rectifiable path 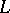 . The specification of the beginning
. The specification of the beginning 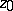 and the end
and the end 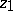 of this path
of this path 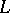 does not determine completely the value of the elliptic integral (1), generally speaking; in other words, (1) is a many-valued function of
does not determine completely the value of the elliptic integral (1), generally speaking; in other words, (1) is a many-valued function of 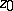 and
and 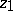 .
.
Any elliptic integral can be expressed as a sum of elementary functions and linear combinations of canonical elliptic integrals of the first, second and third kinds. The latter can be written, for example, in the following form:
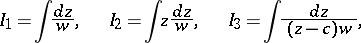 |
where  is the parameter of the elliptic integral of the third kind.
is the parameter of the elliptic integral of the third kind.
The differential 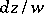 corresponding to
corresponding to 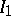 is finite everywhere on the Riemann surface
is finite everywhere on the Riemann surface  , the differentials of the second kind and third kinds have a pole-type singularity with residue zero or a simple pole, respectively. Regarded as functions of the upper limit of integration with a fixed lower limit, these three elliptic integrals are many-valued on
, the differentials of the second kind and third kinds have a pole-type singularity with residue zero or a simple pole, respectively. Regarded as functions of the upper limit of integration with a fixed lower limit, these three elliptic integrals are many-valued on 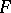 . If one cuts
. If one cuts 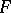 along two cycles of a homology basis, then on the resulting simply-connected domain
along two cycles of a homology basis, then on the resulting simply-connected domain 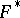 the integrals
the integrals 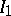 and
and 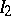 are single valued, while
are single valued, while 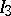 still has a logarithmic singularity that arises on going around the simple pole. On passing through a cut each integral changes by an integer multiple of the corresponding period or modulus of periodicity, while
still has a logarithmic singularity that arises on going around the simple pole. On passing through a cut each integral changes by an integer multiple of the corresponding period or modulus of periodicity, while 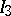 has in addition a third logarithmic period
has in addition a third logarithmic period 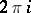 corresponding to a circuit around the singular point. Thus, the computation of an integral of type (1) reduces to that of an integral along the path
corresponding to a circuit around the singular point. Thus, the computation of an integral of type (1) reduces to that of an integral along the path 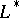 on
on 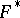 joining the points
joining the points  and
and 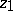 , and the addition of the corresponding linear combination of periods.
, and the addition of the corresponding linear combination of periods.
By subjecting the variable  to certain transformations one can bring the function
to certain transformations one can bring the function 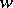 and the basic elliptic integrals to normal forms. In Weierstrass normal form the relation
and the basic elliptic integrals to normal forms. In Weierstrass normal form the relation
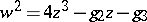 |
holds, and the integral
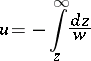 |
has the periods 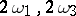 . The inversion of this elliptic integral gives the Weierstrass elliptic function
. The inversion of this elliptic integral gives the Weierstrass elliptic function 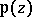 with periods
with periods 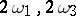 and invariants
and invariants 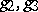 (see Weierstrass elliptic functions). The calculation of the periods
(see Weierstrass elliptic functions). The calculation of the periods 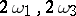 from given invariants proceeds by means of the modular function
from given invariants proceeds by means of the modular function 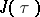 . If in a normal integral of the second kind
. If in a normal integral of the second kind
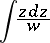 |
one takes a normal integral of the first kind  as integration variable, then for a suitable choice of the integration constant the equality
as integration variable, then for a suitable choice of the integration constant the equality
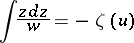 |
holds, where 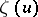 is the Weierstrass
is the Weierstrass 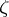 -function. Here the periods of the normal integral of the second kind are equal to
-function. Here the periods of the normal integral of the second kind are equal to  ,
, 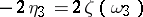 . A normal integral of the third kind in Weierstrass form has the form
. A normal integral of the third kind in Weierstrass form has the form
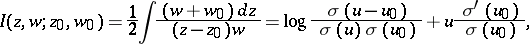 |
where 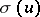 is the Weierstrass
is the Weierstrass 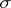 -function,
-function, 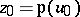 ,
,  ,
, 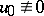
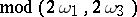 . Here the transposition rule holds:
. Here the transposition rule holds:
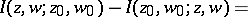 |
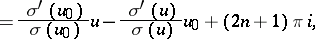 |
where  is an integer. The periods of a normal integral of the third kind have the form
is an integer. The periods of a normal integral of the third kind have the form
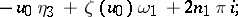 |
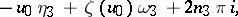 |
where 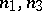 are integers and
are integers and 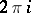 is the logarithmic period.
is the logarithmic period.
In applications on often comes across the Legendre normal form. Here
 |
where 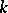 is called the modulus of the elliptic integral,
is called the modulus of the elliptic integral, 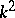 is sometimes called the Legendre modulus, and
is sometimes called the Legendre modulus, and 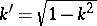 is called the supplementary modulus. Most frequently the normal case occurs, when
is called the supplementary modulus. Most frequently the normal case occurs, when 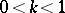 and
and 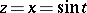 is a real variable. An elliptic integral of the first kind in Legendre normal form has the form
is a real variable. An elliptic integral of the first kind in Legendre normal form has the form
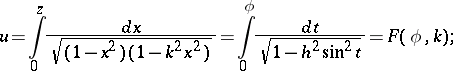 |
it is also called an incomplete elliptic integral of the first kind; 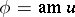 is called its amplitude. This is an infinite-valued function of
is called its amplitude. This is an infinite-valued function of  . The inversion of a normal integral of the first kind leads to the Jacobi elliptic function
. The inversion of a normal integral of the first kind leads to the Jacobi elliptic function 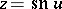 (see Jacobi elliptic functions).
(see Jacobi elliptic functions).
The Legendre normal form of a normal integral of the second kind is
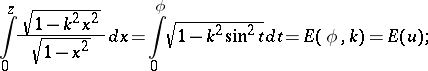 |
it is also called an incomplete elliptic integral of the second kind.
The integrals
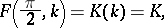 |
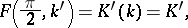 |
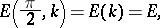 |
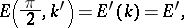 |
are called complete elliptic integrals of the first and second kind, respectively. The Legendre integrals of the first kind have periods 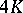 and
and 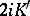 , those of the second kind —
, those of the second kind — 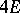 and
and 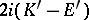 .
.
The Legendre normal form of a normal integral of the third kind is
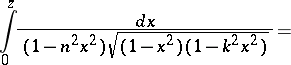 |
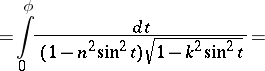 |
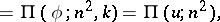 |
where 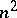 is the parameter and, as a rule,
is the parameter and, as a rule, 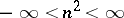 . When
. When 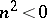 or
or 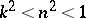 , it is called a circular integral, and when
, it is called a circular integral, and when 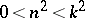 or
or 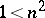 — a hyperbolic integral.
— a hyperbolic integral.
A normal integral of the third kind according to Jacobi is defined somewhat differently:
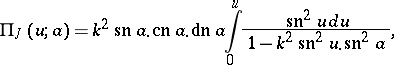 |
where 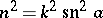 . The connection between Jacobi and Legendre integrals of the third kind can be expressed by the formula
. The connection between Jacobi and Legendre integrals of the third kind can be expressed by the formula
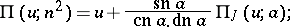 |
a circular character corresponds to an imaginary  and a hyperbolic one to a real
and a hyperbolic one to a real  .
.
Side-by-side with elliptic functions, elliptic integrals have numerous and important applications in various problems of analysis, geometry and physics; in particular, in mechanics, astronomy and geodesy. There are tables of elliptic integrals and extensive guidebooks on the theory of elliptic integrals and functions, and also compendia of formulas.
For references see also Elliptic function.
References
| [1] | V.M. Belyakov, R.I. Kravtsova, M.G. Rappoport, "Tables of elliptic integrals" , 1–2 , Moscow (1962–1963) (In Russian) |
| [2] | E. Jahnke, F. Emde, "Tables of functions with formulae and curves" , Dover, reprint (1945) (Translated from German) MR0015900 Zbl 0061.29906 |
Comments
References
| [a1] | H. Hancock, "Theory of elliptic functions" , Dover, reprint (1958) MR0100106 Zbl 0084.07302 |
| [a2] | M. Abramowitz, I.A. Stegun, "Handbook of mathematical functions" , Dover, reprint (1972) MR0314236 Zbl 0543.33001 |
Elliptic integral. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Elliptic_integral&oldid=35069