Cardioid

A plane algebraic curve of order four which is described by a point $M$ of a circle of radius $r$ rolling on a circle with the same radius $r$; an epicycloid with modulus $m=1$. The equation of the cardioid in polar coordinates is:

$$\rho=2r(1-\cos\phi),$$

In Cartesian coordinates it is:

$$(x^2+y^2+2rx)^2=4r^2(x^2+y^2).$$

The arc length from the cusp is:

$$l=16r\sin^2\frac\phi4.$$

The radius of curvature is:

$$r_k=\frac{8r}{3}\sin\frac\phi2.$$

The area bounded by the curve equals $S=6\pi r^2$. The length of the curve is $16r$. The cardioid is a conchoid of the circle, a special case of a Pascal limaçon and a sinusoidal spiral.

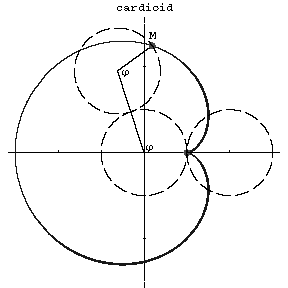
Figure: c020390a

References

[1]	A.A. Savelov, "Planar curves" , Moscow (1960) (In Russian)

[a1]	J.D. Lawrence, "A catalog of special plane curves" , Dover, reprint (1972)