Difference between revisions of "Rank"
(Importing text file) |
Ulf Rehmann (talk | contribs) m (MR/ZBL numbers added) |
||
| Line 16: | Line 16: | ||
The invariant basis number property is also called the invariant dimension property. | The invariant basis number property is also called the invariant dimension property. | ||
| − | For matrices over skew-fields one considers two ranks, which need not be equal: 1) the rank of the rows considered in a left vector space (it equals the rank of the columns considered in a right vector space); and 2) the rank obtained by interchanging | + | For matrices over skew-fields one considers two ranks, which need not be equal: 1) the rank of the rows considered in a left vector space (it equals the rank of the columns considered in a right vector space); and 2) the rank obtained by interchanging "left" and "right" in 1). |
====References==== | ====References==== | ||
| − | <table><TR><TD valign="top">[a1]</TD> <TD valign="top"> | + | <table><TR><TD valign="top">[a1]</TD> <TD valign="top"> P.M. Cohn, "Algebra" , '''1–3''' , Wiley (1988) {{MR|0949350}} {{ZBL|1079.16013}} {{ZBL|1006.00001}} {{ZBL|1003.00001}} {{ZBL|1031.16018}} {{ZBL|1016.20033}} {{ZBL|0952.00001}} {{ZBL|0809.15001}} {{ZBL|0719.00002}} {{ZBL|0674.10023}} {{ZBL|0703.00002}} {{ZBL|0481.00001}} {{ZBL|0461.08001}} {{ZBL|0341.00002}} {{ZBL|0314.68032}} {{ZBL|0272.00003}} {{ZBL|0217.50302}} {{ZBL|0169.32601}} {{ZBL|0141.01002}} {{ZBL|0127.26402}} </TD></TR><TR><TD valign="top">[a2]</TD> <TD valign="top"> N. Bourbaki, "Elements of mathematics. Algebra I" , Addison-Wesley (1974) pp. Chapt. II (Translated from French) {{MR|0354207}} {{ZBL|0281.00006}} </TD></TR></table> |
Revision as of 14:51, 24 March 2012
A concept closely connected with the concept of a basis. Usually rank is defined either as the minimal cardinality of a generating set (in this way, for example, one introduces the basis rank of an algebraic system), or as the maximal cardinality of a subsystem of elements which are independent in a certain sense.
The rank of a system of a vectors in a vector space over a skew-field is the maximal number of linearly independent vectors in this system (see Linear independence). The rank, or dimension, of a vector space, in particular, is equal to the number of elements in a basis of this space (the rank does not depend on the choice of the basis: all bases have the same cardinality). For a module the situation is more complicated. There exist associative rings 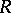 such that even a free module over
such that even a free module over 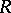 can have two bases with a different number of elements (see Rank of a module; Free module). If each free
can have two bases with a different number of elements (see Rank of a module; Free module). If each free 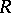 -module has a unique rank, then
-module has a unique rank, then 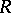 is said to have the invariant basis number property. Every commutative associative ring with a unit is such, so one can define, for example, the (Prüfer) rank of an Abelian group (which can be considered as a module over the ring
is said to have the invariant basis number property. Every commutative associative ring with a unit is such, so one can define, for example, the (Prüfer) rank of an Abelian group (which can be considered as a module over the ring 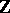 ). In the non-Abelian case two concepts of the rank of a group are introduced, the general and the special rank (see Rank of a group). One defines the rank of an algebraic group and the rank of a Lie group in a special way.
). In the non-Abelian case two concepts of the rank of a group are introduced, the general and the special rank (see Rank of a group). One defines the rank of an algebraic group and the rank of a Lie group in a special way.
The rank of an algebra (over a skew-field) is understood to be the rank of its additive vector space. However, there exists another, unrelated, concept of rank in the theory of Lie algebras (see Rank of a Lie algebra).
The rank of a matrix is defined as the rank of the system of vectors forming its rows (row rank) or of the system of columns (column rank). For matrices over a commutative ring with a unit these two concepts of rank coincide. For a matrix over a field the rank is also equal to the maximal order of a non-zero minor. The rank of a product of matrices is not greater than the rank of each of the factors. The rank of a matrix does not change under multiplication by a non-singular matrix.
The rank of a linear mapping is the dimension of the image under this mapping. In the finite-dimensional case it coincides with the rank of a matrix of this mapping.
One also introduces the concept of the rank of a bilinear form (see Bilinear form) and the rank of a quadratic form (see Quadratic form). They also (in the finite-dimensional case) coincide with the rank of a matrix of the corresponding form.
Comments
The invariant basis number property is also called the invariant dimension property.
For matrices over skew-fields one considers two ranks, which need not be equal: 1) the rank of the rows considered in a left vector space (it equals the rank of the columns considered in a right vector space); and 2) the rank obtained by interchanging "left" and "right" in 1).
References
| [a1] | P.M. Cohn, "Algebra" , 1–3 , Wiley (1988) MR0949350 Zbl 1079.16013 Zbl 1006.00001 Zbl 1003.00001 Zbl 1031.16018 Zbl 1016.20033 Zbl 0952.00001 Zbl 0809.15001 Zbl 0719.00002 Zbl 0674.10023 Zbl 0703.00002 Zbl 0481.00001 Zbl 0461.08001 Zbl 0341.00002 Zbl 0314.68032 Zbl 0272.00003 Zbl 0217.50302 Zbl 0169.32601 Zbl 0141.01002 Zbl 0127.26402 |
| [a2] | N. Bourbaki, "Elements of mathematics. Algebra I" , Addison-Wesley (1974) pp. Chapt. II (Translated from French) MR0354207 Zbl 0281.00006 |
Rank. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Rank&oldid=21914