Difference between revisions of "Weil algebra"
m (AUTOMATIC EDIT (latexlist): Replaced 69 formulas out of 72 by TEX code with an average confidence of 2.0 and a minimal confidence of 2.0.) |
m (Automatically changed introduction) |
||
| Line 2: | Line 2: | ||
the semi-automatic procedure described at https://encyclopediaofmath.org/wiki/User:Maximilian_Janisch/latexlist | the semi-automatic procedure described at https://encyclopediaofmath.org/wiki/User:Maximilian_Janisch/latexlist | ||
was used. | was used. | ||
| − | If the TeX and formula formatting is correct, please remove this message and the {{TEX|semi-auto}} category. | + | If the TeX and formula formatting is correct and if all png images have been replaced by TeX code, please remove this message and the {{TEX|semi-auto}} category. |
Out of 72 formulas, 69 were replaced by TEX code.--> | Out of 72 formulas, 69 were replaced by TEX code.--> | ||
| − | {{TEX|semi-auto}}{{TEX| | + | {{TEX|semi-auto}}{{TEX|part}} |
Motivated by [[Algebraic geometry|algebraic geometry]], A. Weil [[#References|[a3]]] suggested the treatment of infinitesimal objects as homomorphisms from algebras of smooth functions $C ^ { \infty } ( \mathbf{R} ^ { m } , \mathbf{R} )$ into some real finite-dimensional commutative algebra $A$ with unit. The points in $\mathbf{R} ^ { m }$ correspond to the choice $A = \mathbf{R}$, while the algebra $\mathcal{D} = \mathbf{R}\cdot 1 \oplus e \cdot \mathbf{R}$, $e ^ { 2 } = 0$, of dual numbers (also called Study numbers) leads to the tangent vectors at points in $\mathbf{R} ^ { m }$ (viewed as derivations on functions). At the same time, Ch. Ehresmann established similar objects, jets (cf. also [[Jet|Jet]]), in the realm of [[Differential geometry|differential geometry]], cf. [[#References|[a1]]]. | Motivated by [[Algebraic geometry|algebraic geometry]], A. Weil [[#References|[a3]]] suggested the treatment of infinitesimal objects as homomorphisms from algebras of smooth functions $C ^ { \infty } ( \mathbf{R} ^ { m } , \mathbf{R} )$ into some real finite-dimensional commutative algebra $A$ with unit. The points in $\mathbf{R} ^ { m }$ correspond to the choice $A = \mathbf{R}$, while the algebra $\mathcal{D} = \mathbf{R}\cdot 1 \oplus e \cdot \mathbf{R}$, $e ^ { 2 } = 0$, of dual numbers (also called Study numbers) leads to the tangent vectors at points in $\mathbf{R} ^ { m }$ (viewed as derivations on functions). At the same time, Ch. Ehresmann established similar objects, jets (cf. also [[Jet|Jet]]), in the realm of [[Differential geometry|differential geometry]], cf. [[#References|[a1]]]. | ||
Revision as of 17:44, 1 July 2020
Motivated by algebraic geometry, A. Weil [a3] suggested the treatment of infinitesimal objects as homomorphisms from algebras of smooth functions $C ^ { \infty } ( \mathbf{R} ^ { m } , \mathbf{R} )$ into some real finite-dimensional commutative algebra $A$ with unit. The points in $\mathbf{R} ^ { m }$ correspond to the choice $A = \mathbf{R}$, while the algebra $\mathcal{D} = \mathbf{R}\cdot 1 \oplus e \cdot \mathbf{R}$, $e ^ { 2 } = 0$, of dual numbers (also called Study numbers) leads to the tangent vectors at points in $\mathbf{R} ^ { m }$ (viewed as derivations on functions). At the same time, Ch. Ehresmann established similar objects, jets (cf. also Jet), in the realm of differential geometry, cf. [a1].
Since $C ^ { \infty } ( \mathbf{R} ^ { m } , \mathbf{R} )$ is formally real (i.e. $1 + a _ { 1 } ^ { 2 } + \ldots + a _ { k } ^ { 2 }$ is invertible for all 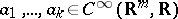 ), the values of the homomorphisms in $\operatorname{Hom}( C ^ { \infty } ( \mathbf{R} ^ { m } , \mathbf{R} ) , A )$ are in formally real subalgebras. Now, for each finite-dimensional real commutative unital algebra $A$ which is formally real, there is a decomposition of the unit $1 = e _ { 1 } + \ldots + e _ { k }$ into all minimal idempotent elements. Thus, $A = A _ { 1 } \oplus \ldots \oplus A _ { k }$, where $A _ { i } = A \cdot e _ { i } = \mathbf{R} \cdot e_{i} \oplus N _ { i }$, and $N_{i}$ are nilpotent ideals in $A_i$. A real unital finite-dimensional commutative algebra $A$ is called a Weil algebra if it is of the form
), the values of the homomorphisms in $\operatorname{Hom}( C ^ { \infty } ( \mathbf{R} ^ { m } , \mathbf{R} ) , A )$ are in formally real subalgebras. Now, for each finite-dimensional real commutative unital algebra $A$ which is formally real, there is a decomposition of the unit $1 = e _ { 1 } + \ldots + e _ { k }$ into all minimal idempotent elements. Thus, $A = A _ { 1 } \oplus \ldots \oplus A _ { k }$, where $A _ { i } = A \cdot e _ { i } = \mathbf{R} \cdot e_{i} \oplus N _ { i }$, and $N_{i}$ are nilpotent ideals in $A_i$. A real unital finite-dimensional commutative algebra $A$ is called a Weil algebra if it is of the form
\begin{equation*} A = {\bf R} .1 \bigoplus N, \end{equation*}
where $N$ is the ideal of all nilpotent elements in $A$. The smallest $r \in \bf N$ with the property $N ^ { r + 1 } = 0$ is called the depth, or order, of $A$.
In other words, one may also characterize the Weil algebras as the formally real and local (i.e. the ring structure is local, cf. also Local ring) finite-dimensional commutative real unital algebras. See [a2], 35.1, for details.
As a consequence of the Nakayama lemma, the Weil algebras can be also characterized as the local finite-dimensional quotients of the algebras of real polynomials $\mathbf{R}[ x _ { 1 } , \dots , x _ { n } ]$. Consequently, the Weil algebras $A$ correspond to choices of ideals $\mathcal{A}$ in $\mathbf{R}[ x _ { 1 } , \dots , x _ { n } ]$ of finite codimension. The algebra of Study numbers $\mathcal{D} = \mathbf{R} [ x ] / D$ is given by $D = \langle x ^ { 2 } \rangle \subset \mathbf{R} [ x ]$, for example. Equivalently, one may consider the algebras of formal power series or the algebras of germs of smooth functions at the origin $0 \in {\bf R} ^ { n }$ (cf. also Germ) instead of the polynomials.
The width of a Weil algebra $A = \mathbf{R} \cdot1 \oplus N$ is defined as the dimension of the vector space $N / N ^ { 2 }$. If $\mathcal{A}$ is an ideal of finite codimension in $\mathbf{R}[ x _ { 1 } , \dots , x _ { n } ]$, ${\cal A} \subset \langle x ^ { 1 } , \ldots , x _ { n } \rangle ^ { 2 }$, then the width of $A = \mathbf{R} [ x _ { 1 } , \dots , x _ { n } ] / \mathcal{A}$ equals $n$. For example, the Weil algebra
\begin{equation*} \mathcal{D} _ { n } ^ { r } = \mathbf{R} [ x _ { 1 } , \ldots , x _ { n } ] / \langle x _ { 1 } , \ldots , x _ { n } \rangle ^ { r + 1 } \end{equation*}
has width $n$ and order $r$, and it coincides with the algebra $J ^{ r_0} ( \mathbf{R} ^ { n } , \mathbf{R} )$ of $r$-jets of smooth functions at the origin in ${\bf R} ^ { n }$. Moreover, each Weil algebra of width $n$ and order $r \geq 1$ is a quotient of $\mathcal{D} _ { n } ^ { r }$.
Tensor products of Weil algebras are Weil algebras again. For instance, $\mathcal{D} \otimes \mathcal{D} = \mathbf{R} [ x , y ] / \langle x ^ { 2 } , y ^ { 2 } \rangle$.
The infinitesimal objects of type $A$ attached to points in $\mathbf{R} ^ { m }$ are simply $A ^ { m } = \mathbf{R} ^ { m } \oplus N ^ { m }$. All smooth functions $f : \mathbf{R} ^ { m } \rightarrow \mathbf{R}$ extend to $f _ { A } : A ^ { m } \rightarrow A$ by the evaluation of the Taylor series (cf. also Whitney extension theorem)
\begin{equation*} f _ { A } ( x + h ) = f ( x ) + \sum _ { | \alpha | \geq 1 } \frac { 1 } { \alpha ! } \frac { \partial ^ { | \alpha | } f } { \partial x ^ { \alpha } } | _ { x } h ^ { \alpha }, \end{equation*}
where $x \in \mathbf{R} ^ { m }$, $h = ( h _ { 1 } , \dots , h _ { m } ) \in N ^ { m } \subset A ^ { m }$, $\alpha = ( \alpha _ { 1 } , \dots , \alpha _ { m } )$ are multi-indices, $h ^ { \alpha } = h _ { 1 } ^ { \alpha _ { 1 } } \ldots h _ { m } ^ { \alpha _ { m } }$. Applying this formula to all components of a mapping $f : \mathbf{R} ^ { m } \rightarrow \mathbf{R} ^ { k }$, one obtains an assignment functorial in both $f$ and $A$. Of course, this definition extends to a functor on all locally defined smooth mappings ${\bf R} ^ { m } \rightarrow {\bf R} ^ { k }$ and so each Weil algebra gives rise to a Weil functor $T _ { A }$. (See Weil bundle for more details.)
The automorphism group  of a Weil algebra is a Lie subgroup (cf. also Lie group) in $\operatorname{GL} ( A )$ and its Lie algebra coincides with the space of all derivations (cf. also Derivation in a ring) on $A$,
of a Weil algebra is a Lie subgroup (cf. also Lie group) in $\operatorname{GL} ( A )$ and its Lie algebra coincides with the space of all derivations (cf. also Derivation in a ring) on $A$, 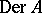 , i.e. all mappings $\delta : A \rightarrow A$ satisfying $\delta ( a b ) = \delta ( a ) b + a \delta ( b )$, cf. [a2], 42.9.
, i.e. all mappings $\delta : A \rightarrow A$ satisfying $\delta ( a b ) = \delta ( a ) b + a \delta ( b )$, cf. [a2], 42.9.
References
| [a1] | Ch. Ehresmann, "Les prolongements d'une variété différentiable. I. Calcul des jets, prolongement principal. II. L'espace des jets d'ordre $r$ de $V _ { n }$ dans $V _ { m }$. III. Transitivité des prolongements" C.R. Acad. Sci. Paris , 233 (1951) pp. 598–600; 777–779; 1081–1083 MR0045436 MR0045435 MR0044198 |
| [a2] | I. Kolář, P.W. Michor, J. Slovák, "Natural operations in differential geometry" , Springer (1993) MR1202431 Zbl 1084.53001 |
| [a3] | A. Weil, "Théorie des points proches sur les variétés differentielles" Colloq. Internat. Centre Nat. Rech. Sci. , 52 (1953) pp. 111–117 |
Weil algebra. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Weil_algebra&oldid=50396