Difference between revisions of "Elliptic surface"
Ulf Rehmann (talk | contribs) m (tex encoded by computer) |
m (fixing superscripts) |
||
| Line 16: | Line 16: | ||
whose generic fibre is a non-singular elliptic curve. Every elliptic surface is birationally (bimeromorphically) equivalent over $ B $ | whose generic fibre is a non-singular elliptic curve. Every elliptic surface is birationally (bimeromorphically) equivalent over $ B $ | ||
to a unique minimal model, which is characterized by the fact that the fibre of $ \pi $ | to a unique minimal model, which is characterized by the fact that the fibre of $ \pi $ | ||
| − | does not contain exceptional curves of arithmetic genus 1. In what follows an elliptic surface is assumed to be minimal. Minimal elliptic surfaces have a more complicated structure than ruled surfaces. They can have singular fibres $ X _ {t} = \pi ^ {-} | + | does not contain exceptional curves of arithmetic genus 1. In what follows an elliptic surface is assumed to be minimal. Minimal elliptic surfaces have a more complicated structure than ruled surfaces. They can have singular fibres $ X _ {t} = \pi ^ {- 1} ( t) $ (that is, fibres that are not non-singular elliptic curves). There is a classification |
| − | that is, fibres that are not non-singular elliptic curves). There is a classification | ||
of the singular fibres of elliptic surfaces. A singular fibre $ X _ {t} = \sum n _ {i} E _ {i} $ | of the singular fibres of elliptic surfaces. A singular fibre $ X _ {t} = \sum n _ {i} E _ {i} $ | ||
| Line 50: | Line 49: | ||
can be regarded as an elliptic curve over the function field $ k ( B) $. | can be regarded as an elliptic curve over the function field $ k ( B) $. | ||
This curve, generally speaking, does not have the structure of an Abelian variety over $ k ( B) $. | This curve, generally speaking, does not have the structure of an Abelian variety over $ k ( B) $. | ||
| − | For this to happen it is necessary that it has a rational point over $ k ( B) $( | + | For this to happen it is necessary that it has a rational point over $ k ( B) $ (and then $ X $ |
| − | and then $ X $ | ||
is birationally isomorphic to the surface defined in $ B \times A ^ {2} $ | is birationally isomorphic to the surface defined in $ B \times A ^ {2} $ | ||
by the Weierstrass equation $ y ^ {2} = x ^ {3} - g _ {2} x - g _ {3} $, | by the Weierstrass equation $ y ^ {2} = x ^ {3} - g _ {2} x - g _ {3} $, | ||
| Line 88: | Line 86: | ||
$$ | $$ | ||
| − | 0 \rightarrow \mathbf Z \rightarrow {\mathcal O} _ {B} \mathop \rightarrow \limits ^ \mathop {\rm exp} | + | 0 \rightarrow \mathbf Z \rightarrow {\mathcal O} _ {B} \mathop \rightarrow \limits ^ {\mathop {\rm exp}} {\mathcal O} _ {B} ^ {*} \rightarrow 1 |
| − | {\mathcal O} _ {B} ^ {*} \rightarrow 1 | ||
$$ | $$ | ||
| Line 102: | Line 99: | ||
is the sheaf of local sections of the bundle $ T ( {\mathcal J} )/ B $ | is the sheaf of local sections of the bundle $ T ( {\mathcal J} )/ B $ | ||
and $ T ( {\mathcal J} ) $ | and $ T ( {\mathcal J} ) $ | ||
| − | is the tangent space to the fibre $ \tau ^ {-} | + | is the tangent space to the fibre $ \tau ^ {- 1 }( b) $ |
at $ e ( b) $. | at $ e ( b) $. | ||
The boundary homomorphism | The boundary homomorphism | ||
| Line 111: | Line 108: | ||
$$ | $$ | ||
| − | allows one to recognize when one fibration is a deformation of another. For that it is necessary and sufficient that the elements corresponding to these fibrations have one and the same image under $ \delta $( | + | allows one to recognize when one fibration is a deformation of another. For that it is necessary and sufficient that the elements corresponding to these fibrations have one and the same image under $ \delta $ (see ). |
| − | see ). | ||
==The classification of algebraic elliptic surfaces.== | ==The classification of algebraic elliptic surfaces.== | ||
| Line 135: | Line 131: | ||
If $ \chi ( {\mathcal O} _ {X} )= 2 $, | If $ \chi ( {\mathcal O} _ {X} )= 2 $, | ||
then $ X $ | then $ X $ | ||
| − | is an elliptic [[K3-surface| $ K 3 $- | + | is an elliptic [[K3-surface| $ K 3 $-surface]] ( $ q = 0 $, |
| − | surface]] ( $ q = 0 $, | ||
$ K _ {X} = 0 $). | $ K _ {X} = 0 $). | ||
In this case $ B $ | In this case $ B $ | ||
| Line 210: | Line 205: | ||
$ \iff $ | $ \iff $ | ||
$ 12K _ {X} = 0 $; | $ 12K _ {X} = 0 $; | ||
| − | and $ k ( X) = 1 $( | + | and $ k ( X) = 1 $ ($ X $ |
| − | $ X $ | ||
is of basic type) $ \iff $ | is of basic type) $ \iff $ | ||
$ | 12 K _ {X} | = \emptyset $, | $ | 12 K _ {X} | = \emptyset $, | ||
| Line 217: | Line 211: | ||
Non-algebraic elliptic surfaces with $ k ( X) = 0 $ | Non-algebraic elliptic surfaces with $ k ( X) = 0 $ | ||
| − | belong to one of the following classes: 1) the $ K 3 $- | + | belong to one of the following classes: 1) the $ K 3 $-surfaces ( $ \chi ( {\mathcal O} _ {X} )= 2 $, |
| − | surfaces ( $ \chi ( {\mathcal O} _ {X} )= 2 $, | ||
$ b _ {1} = 0 $, | $ b _ {1} = 0 $, | ||
$ b _ {2} = 22 $, | $ b _ {2} = 22 $, | ||
| Line 230: | Line 223: | ||
$ b _ {1} = 3 $, | $ b _ {1} = 3 $, | ||
$ b _ {2} = 4 $). | $ b _ {2} = 4 $). | ||
| − | Primary Kodaira surfaces are holomorphically locally trivial fibrations over an elliptic curve with an elliptic curve as typical fibre, and from the point of view of differentiability, bundles over a $ 3 $- | + | Primary Kodaira surfaces are holomorphically locally trivial fibrations over an elliptic curve with an elliptic curve as typical fibre, and from the point of view of differentiability, bundles over a $ 3 $-dimensional torus with a circle as fibre; or 4) the surfaces with $ \chi ( {\mathcal O} _ {X} ) = 0 $, |
| − | dimensional torus with a circle as fibre; or 4) the surfaces with $ \chi ( {\mathcal O} _ {X} ) = 0 $, | ||
$ p _ {g} = 0 $, | $ p _ {g} = 0 $, | ||
$ b _ {1} = 1 $, | $ b _ {1} = 1 $, | ||
| Line 258: | Line 250: | ||
The canonical dimension $ k ( X) $ | The canonical dimension $ k ( X) $ | ||
| − | mentioned at the start of the section on classification of algebraic elliptic surfaces is the [[Kodaira dimension|Kodaira dimension]] $ \mathop{\rm Kod} ( X) $( | + | mentioned at the start of the section on classification of algebraic elliptic surfaces is the [[Kodaira dimension|Kodaira dimension]] $ \mathop{\rm Kod} ( X) $ (with $ k ( X) = - 1 $ |
| − | with $ k ( X) = - 1 $ | ||
if $ \mathop{\rm Kod} ( X) = - \infty $). | if $ \mathop{\rm Kod} ( X) = - \infty $). | ||
====References==== | ====References==== | ||
<table><TR><TD valign="top">[a1]</TD> <TD valign="top"> W. Barth, C. Peters, A. van der Ven, "Compact complex surfaces" , Springer (1984) {{MR|0749574}} {{ZBL|0718.14023}} </TD></TR></table> | <table><TR><TD valign="top">[a1]</TD> <TD valign="top"> W. Barth, C. Peters, A. van der Ven, "Compact complex surfaces" , Springer (1984) {{MR|0749574}} {{ZBL|0718.14023}} </TD></TR></table> | ||
Latest revision as of 05:46, 13 June 2022
An algebraic or analytic complete non-singular surface $ X $
having a fibration of elliptic curves (cf. Elliptic curve), that is, a morphism $ \pi : X \rightarrow B $
onto a non-singular curve $ B $
whose generic fibre is a non-singular elliptic curve. Every elliptic surface is birationally (bimeromorphically) equivalent over $ B $
to a unique minimal model, which is characterized by the fact that the fibre of $ \pi $
does not contain exceptional curves of arithmetic genus 1. In what follows an elliptic surface is assumed to be minimal. Minimal elliptic surfaces have a more complicated structure than ruled surfaces. They can have singular fibres $ X _ {t} = \pi ^ {- 1} ( t) $ (that is, fibres that are not non-singular elliptic curves). There is a classification
of the singular fibres of elliptic surfaces. A singular fibre $ X _ {t} = \sum n _ {i} E _ {i} $ is called multiple if the greatest common divisor of the $ n _ {i} $ is $ m \geq 2 $, and then $ X _ {t} = m F $ and $ m $ is called the multiplicity of the fibre $ X _ {t} $.
On a minimal elliptic surface the canonical class $ K _ {X} $ contains a divisor that is a rational combination of fibres, in particular, $ ( K _ {X} ^ {2} ) = 0 $. Moreover, the following formula holds for the canonical class (see [1], ):
$$ K _ {X} = \pi ^ {*} ( K _ {B} - d ) + \sum ( m _ {i} - 1 ) F _ {i} , $$
where $ X _ {t _ {i} } = m _ {i} F _ {i} $ are all the multiple fibres of $ \pi $ and $ d $ is a divisor on $ B $ of degree $ - \chi ( {\mathcal O} _ {X} ) $. The topological Euler characteristic satisfies the formula
$$ e ( X) = \sum e ( X _ {t _ {i} } ) . $$
The classification of elliptic fibrations.
A fibration $ \pi : X \rightarrow B $ can be regarded as an elliptic curve over the function field $ k ( B) $. This curve, generally speaking, does not have the structure of an Abelian variety over $ k ( B) $. For this to happen it is necessary that it has a rational point over $ k ( B) $ (and then $ X $ is birationally isomorphic to the surface defined in $ B \times A ^ {2} $ by the Weierstrass equation $ y ^ {2} = x ^ {3} - g _ {2} x - g _ {3} $, where $ g _ {2} , g _ {3} \in k ( B) $). The specification of a rational point is equivalent to that of a section $ e : B \rightarrow X $ such that $ \pi e = \mathop{\rm id} $; a necessary condition for the existence of a section is the absence of multiple fibres. Fibrations without multiple fibres are called reduced. Every fibration, after a suitable ramified covering of the base, has a section (that is, is reduced) . Every fibration can also be made reduced by a sequence of transformations inverse to logarithmic ones
— local surgery of the fibration in neighbourhoods of fibres.
Reduced elliptic fibrations may be described as follows. To every such fibration $ \pi : X \rightarrow B $ corresponds a unique fibration $ {\mathcal J} _ {B} ( X) \rightarrow B $ that is a group object and is such that $ X / B $ is a principal homogeneous space over $ {\mathcal J} _ {B} ( X) / B $; $ {\mathcal J} _ {B} ( X) / B $ is the Jacobi fibration for $ X / B $; it characterizes the existence of a section. For a given Jacobi fibration $ {\mathcal J} / B $, the set $ I ( {\mathcal J} / B ) $ of isomorphism classes of fibrations $ X / B $ for which $ {\mathcal J} _ {B} ( X) \cong J $ has a cohomology description analogous to that of invertible sheaves (cf. Invertible sheaf). Here the role of $ {\mathcal O} _ {B} ^ {*} $ is played by the sheaf $ {\mathcal H} ^ {0} ( {\mathcal J} / B ) $ of local sections $ \tau : {\mathcal J} \rightarrow B $. There is a natural one-to-one correspondence
$$ \theta : I ( {\mathcal J} / B ) \rightarrow H ^ {1} ( B , {\mathcal H} ^ {0} ( {\mathcal J} / B ) ) , $$
under which the Jacobi fibration corresponds to the zero element. By means of $ \theta $ one can distinguish between algebraic and non-algebraic fibrations: For a reduced fibration $ \pi : X \rightarrow B $ the surface $ X $ is algebraic if and only if the element corresponding to it in $ H ^ {1} ( B , {\mathcal H} ^ {0} ( {\mathcal J} / B )) $ is of finite order. The analogy with invertible sheaves can be pursued further. The analogue of the exact sequence
$$ 0 \rightarrow \mathbf Z \rightarrow {\mathcal O} _ {B} \mathop \rightarrow \limits ^ {\mathop {\rm exp}} {\mathcal O} _ {B} ^ {*} \rightarrow 1 $$
is the exact sequence
$$ 0 \rightarrow R ^ {1} \tau _ {0} \mathbf Z \rightarrow {\mathcal H} ^ {0} ( T ( {\mathcal J} ) / B ) \rightarrow {\mathcal H} ^ {0} ( {\mathcal J} / B ) \rightarrow 0 , $$
where $ {\mathcal H} ^ {0} ( T ( {\mathcal J} ) / B ) $ is the sheaf of local sections of the bundle $ T ( {\mathcal J} )/ B $ and $ T ( {\mathcal J} ) $ is the tangent space to the fibre $ \tau ^ {- 1 }( b) $ at $ e ( b) $. The boundary homomorphism
$$ \delta : H ^ {1} ( B , {\mathcal H} ^ {0} ( {\mathcal J} / B ) ) \rightarrow H ^ {2} ( B , R ^ {1} \tau _ {*} \mathbf Z ) $$
allows one to recognize when one fibration is a deformation of another. For that it is necessary and sufficient that the elements corresponding to these fibrations have one and the same image under $ \delta $ (see ).
The classification of algebraic elliptic surfaces.
Suppose that $ \mathop{\rm char} k = 0 $. For an elliptic surface $ X $ the canonical dimension $ k ( X) \leq 1 $, that is, it is equal to $ - 1 $, 0 or $ 1 $. If $ k ( X) = 1 $, $ X $ is said to be an elliptic surface of general type. These are characterized by the conditions $ 12 K _ {X} \neq 0 $ and $ | 12 K _ {X} | \neq \emptyset $. Elliptic surfaces with $ p _ {g} \geq 2 $ or, more generally, with $ P _ {m} \geq 2 $ for some $ m $, are of general type.
Elliptic surfaces with $ k ( X) = 0 $ are characterized by the condition $ 12 K _ {X} = 0 $. In this case $ \chi ( {\mathcal O} _ {X} ) $ can take the three values 2, 1 or $ 0 $. If $ \chi ( {\mathcal O} _ {X} )= 2 $, then $ X $ is an elliptic $ K 3 $-surface ( $ q = 0 $, $ K _ {X} = 0 $). In this case $ B $ is isomorphic to the projective line $ P ^ {1} $, the fibration has no multiple fibres and $ X $ has the invariants $ p _ {g} = 1 $, $ q = 0 $, $ b _ {2} = 22 $. If $ \chi ( {\mathcal O} _ {X} ) = 1 $, then $ X $ is an Enriques surface, that is, a surface with $ p _ {g} = q = 0 $, $ 2 K _ {X} = 0 $. (Every Enriques surface is elliptic.) In this case $ B \simeq P ^ {1} $, the fibration has two fibres of multiplicity 2, and $ X $ has the invariants $ p _ {g} = q = 0 $, $ b _ {2} = 10 $. If $ \chi ( {\mathcal O} _ {X} ) = 0 $, then two cases are possible. Either $ X $ is an Abelian variety (and then $ p _ {g} = 1 $, $ q = 2 $, $ b _ {2} = 6 $); or $ X $ is a hyper-elliptic surface, that is, a surface that has a finite unramified covering — the product of two elliptic curves. In that case $ p _ {g} = 0 $, $ b _ {1} = 2 $, $ b _ {2} = 2 $, $ B = P ^ {1} $, and $ \pi $ has 3 or 4 multiple fibres with four possibilities for their multiplicity: $ ( 3 , 3 , 3 ) $, $ ( 2 , 4 , 4 ) $, $ ( 2 , 3 , 6 ) $, and $ ( 2 , 2 , 2 , 2 ) $, and $ 3 K _ {X} = 0 $, $ 4 K _ {X} = 0 $, $ 6 K _ {X} = 0 $, and $ 2 K _ {X} = 0 $, respectively.
An elliptic surface with $ k ( X) = - 1 $ is ruled (cf. Ruled surface). It is characterized by the condition $ | 12 K _ {X} | = \emptyset $. Here two cases are possible: 1) $ X $ is a surface with $ p _ {g} = q = 0 $, $ b _ {2} = 10 $, and $ \pi $ has no multiple fibres or one; moreover, a surface without multiple fibres can be obtained as follows: one has to take a rational mapping $ P ^ {2} \rightarrow P ^ {1} $ determined by two cubics $ F _ {0} $ and $ F _ {1} $ and blow up their 9 points of intersection; or 2) $ X $ is a surface with $ p _ {g} = 0 $, $ q = 1 $, $ b _ {2} = 2 $, and the multiplicities $ m _ {i} $ are subject to the inequality
$$ \sum \left ( 1 - \frac{1}{m _ {i} } \right ) < 2 . $$
The formula for the canonical class and the classification of elliptic surfaces can also be generalized to the case of a field of finite characteristic [5], [6].
The classification of non-algebraic elliptic surfaces.
The classification of non-algebraic elliptic surfaces. For non-algebraic surfaces the algebraic dimension $ a ( X) = \mathop{\rm tr} \mathop{\rm deg} M ( X) $ is 1 or 0. If $ a ( X) = 0 $, then $ X $ is non-elliptic. All surfaces with $ a ( X) = 1 $ are elliptic. Here the structure of $ \pi : X \rightarrow B $ is determined almost canonically: Every such fibration $ \pi $ is necessarily elliptic. The classification by the canonical dimension is precisely the same as for algebraic elliptic surfaces: $ k ( X) = - 1 $ $ \iff $ $ | 12 K _ {X} | = \emptyset $; $ k ( X) = 0 $ $ \iff $ $ 12K _ {X} = 0 $; and $ k ( X) = 1 $ ($ X $ is of basic type) $ \iff $ $ | 12 K _ {X} | = \emptyset $, $ 12 K _ {X} \neq 0 $.
Non-algebraic elliptic surfaces with $ k ( X) = 0 $ belong to one of the following classes: 1) the $ K 3 $-surfaces ( $ \chi ( {\mathcal O} _ {X} )= 2 $, $ b _ {1} = 0 $, $ b _ {2} = 22 $, $ X $ is simply connected); 2) the complex tori ( $ K _ {X} = 0 $, $ \chi ( {\mathcal O} _ {X} ) = 0 $, $ b _ {1} = 4 $, $ b _ {2} = 6 $); 3) the Kodaira surfaces ( $ K _ {X} = 0 $, $ \chi ( {\mathcal O} _ {X} ) = 0 $, $ b _ {1} = 3 $, $ b _ {2} = 4 $). Primary Kodaira surfaces are holomorphically locally trivial fibrations over an elliptic curve with an elliptic curve as typical fibre, and from the point of view of differentiability, bundles over a $ 3 $-dimensional torus with a circle as fibre; or 4) the surfaces with $ \chi ( {\mathcal O} _ {X} ) = 0 $, $ p _ {g} = 0 $, $ b _ {1} = 1 $, $ b _ {2} = 0 $. For them $ m K _ {X} = 0 $ with $ m = 2 , 3 , 4 $, (analogous to hyper-elliptic surfaces). They have Kodaira surfaces as finite unramified coverings. In the cases 2), 3) and 4) $ \mathbf C ^ {2} $ is the universal covering of $ X $.
Non-algebraic elliptic surfaces with $ k ( X) = - 1 $ are Hopf surfaces, that is, their universal covering is $ \mathbf C ^ {2} \setminus 0 $. For them $ \chi ( {\mathcal O} _ {X} ) = 0 $, $ b _ {1} = 1 $, $ b _ {2} = 0 $. The proper Hopf surfaces are $ ( \mathbf C ^ {2} \setminus 0 ) / T $, where $ T ( z _ {1} , z _ {2} ) = ( \alpha _ {1} z _ {1} , \alpha _ {2} z _ {2} ) $ are real generators of $ T $. They are homeomorphic to $ S ^ {1} \times S ^ {2} $ and are characterized by this property. Arbitrary elliptic Hopf surfaces are quotients of proper Hopf surfaces .
References
| [1] | "Algebraic surfaces" Proc. Steklov Inst. Math. , 75 (1967) Trudy Mat. Inst. Steklov. , 75 (1965) Zbl 0172.37901 Zbl 0153.22401 |
| [2] | D. Husemoller, "Classification and embeddings of surfaces" R. Hartshorne (ed.) , Algebraic geometry (Arcata, 1974) , Proc. Symp. Pure Math. , 29 , Amer. Math. Soc. (1982) pp. 329–420 MR0506292 Zbl 0326.14009 |
| [3a] | K. Kodaira, "On compact complex analytic surfaces I" Ann. of Math. (2) , 71 (10) pp. 111–152 MR0132556 Zbl 0137.17501 Zbl 0098.13004 |
| [3b] | K. Kodaira, "On compact complex analytic surfaces II" Ann. of Math. (2) , 77 (1963) pp. 563–626 MR165541 Zbl 0193.37701 Zbl 0133.16505 |
| [3c] | K. Kodaira, "On compact complex analytic surfaces III" Ann. of Math. (2) , 78 (1963) pp. 1–40 MR165541 Zbl 0193.37701 |
| [4a] | K. Kodaira, "On the structure of compact complex analytic surfaces I" Amer. J. Math. , 86 (1964) pp. 751–798 MR0187255 Zbl 0137.17501 |
| [4b] | K. Kodaira, "On the structure of compact complex analytic surfaces II" Amer. J. Math. , 88 (1966) pp. 682–721 MR0205280 Zbl 0193.37701 |
| [4c] | K. Kodaira, "On the structure of compact complex analytic surfaces III" Amer. J. Math. , 90 (1968) pp. 55–83 MR0228019 Zbl 0193.37701 |
| [4d] | K. Kodaira, "On the structure of compact complex analytic surfaces IV" Amer. J. Math. , 90 (1968) pp. 1048–1066 MR239114 |
| [5] | D. Mumford, "Enriques' classification of surfaces in char 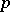 . I" D.C. Spencer (ed.) S. Iyanaga (ed.) , Global analysis (papers in honor of K. Kodaira) , Princeton Univ. Press (1969) pp. 325–339 MR0491719 MR0491720 . I" D.C. Spencer (ed.) S. Iyanaga (ed.) , Global analysis (papers in honor of K. Kodaira) , Princeton Univ. Press (1969) pp. 325–339 MR0491719 MR0491720 |
| [6] | E. Bombieri, D. Mumford, "Enriques' classification of surfaces in char 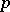 . II" W.L. Baily jr. (ed.) T. Shioda (ed.) , Complex Analysis and Algebraic geometry , Cambridge Univ. Press & Iwanami Shoten (1977) pp. 23–42 MR0491719 MR0491720 . II" W.L. Baily jr. (ed.) T. Shioda (ed.) , Complex Analysis and Algebraic geometry , Cambridge Univ. Press & Iwanami Shoten (1977) pp. 23–42 MR0491719 MR0491720 |
Comments
A secondary Kodaira surface is a surface other than a primary one, admitting a primary Kodaira surface as an unramified covering. They are elliptic fibrations over a rational curve. Their first Betti number is 1.
The canonical dimension $ k ( X) $ mentioned at the start of the section on classification of algebraic elliptic surfaces is the Kodaira dimension $ \mathop{\rm Kod} ( X) $ (with $ k ( X) = - 1 $ if $ \mathop{\rm Kod} ( X) = - \infty $).
References
| [a1] | W. Barth, C. Peters, A. van der Ven, "Compact complex surfaces" , Springer (1984) MR0749574 Zbl 0718.14023 |
Elliptic surface. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Elliptic_surface&oldid=46817