Isogonal

Literally "same angle" . There are several concepts in mathematics involving isogonality.

Isogonal trajectory.

A trajectory that meets a given family of curves at a constant angle. See Isogonal trajectory.

Isogonal mapping.

A (differentiable) mapping that preserves angles. For instance, the stereographic projection of cartography has this property [a2]. See also Conformal mapping; Anti-conformal mapping.

Isogonal circles.

A circle is said to be isogonal with respect to two other circles if it makes the same angle with these two, [a1].

Isogonal line.

Given a triangle 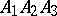and a line 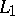from one of the vertices, say from 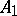, to the opposite side. The corresponding isogonal line 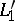is obtained by reflecting 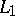with respect to the bisectrix in .

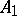If the lines 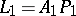, and 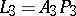are concurrent (i.e. pass through a single point 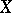, i.e. are Cevian lines), then so are the isogonal lines 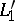, , 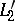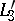. This follows fairly directly from the Ceva theorem. The point 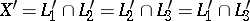is called the isogonal conjugate point. If the barycentric coordinates of 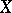(often called trilinear coordinates in this setting) are 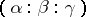, then those of 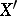are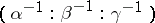

Figure: i130080a

Another notion in rather the same spirit is that of the isotomic line to 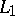, which is the line 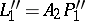such that 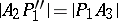. Again it is true that if 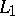, , 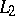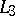are concurrent, then so are 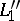, , 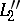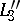. This follows directly from the Ceva theorem.

Figure: i130080b

The point 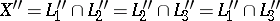is called the isotomic conjugate point. The barycentric coordinates of 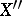are 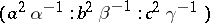, where , , 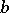are the lengths of the sides of the triangle. The Gergonne point is the isotomic conjugate of the Nagel point.

The involutions 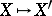and , i.e. isogonal conjugation and isotomic conjugation, are better regarded as involutions of the projective plane 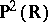, [a4].

References

[a1]	M. Berger, "Geometry" , I , Springer (1987) pp. 327
[a2]	D. Hilbert, S. Cohn-Vossen, "Geometry and the imagination" , Chelsea (1952) pp. 249
[a3]	R.A. Johnson, "Modern geometry" , Houghton–Mifflin (1929)
[a4]	R.H. Eddy, J.B. Wilker, "Plane mappings of isogonal-isotomic type" Soochow J. Math. , 18 : 2 (1992) pp. 135–158
[a5]	N. Altshiller–Court, "College geometry" , Barnes & Noble (1952)
[a6]	H.S.M. Coxeter, "The real projective plane" , Springer (1993) pp. 197–199 (Edition: Third)
[a7]	F. Bachmann, "Aufbau der Geometrie aus dem Spiegelungsbegriff" , Springer (1973) (Edition: Second)