Difference between revisions of "Tree"
(better) |
m (move comment around) |
||
| (11 intermediate revisions by the same user not shown) | |||
| Line 13: | Line 13: | ||
''in graph theory'' | ''in graph theory'' | ||
| − | A connected non-oriented [[Graph|graph]] | + | A connected non-oriented [[Graph|graph]] $G$ which does not contain cycles. A tree has no multiple edges and no loops. Since they are the simplest possible connected graphs, trees are suitable models for the study of various problems in graph theory. Any tree with $n$ |
| − | which does not contain cycles. A tree has no multiple edges and no loops. Since they are the simplest possible | + | vertices contains $n - 1$ |
| − | vertices contains | + | edges. The number of different trees which may be constructed on $n$ |
| − | edges. The number of different trees which may be constructed on $ | + | numbered vertices is $n^{n-2}$. |
| − | numbered vertices is | + | |
| − | A tree with one distinguished vertex is said to be a rooted tree. | + | A tree with one distinguished vertex is said to be a [[rooted tree]]. A '''forest''' is a graph without cycles: every connected component of a forest is a tree. |
| + | |||
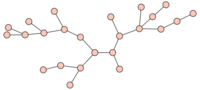
| + | [[File:Some_tree.svg|center|200px|Example of tree]] | ||
| + | |||
| + | == Enumeration == | ||
The enumerating series | The enumerating series | ||
| Line 48: | Line 52: | ||
$$ | $$ | ||
| − | t ( x) = T ( x) - | + | t ( x) = T ( x) - \frac{T ^ {2} ( x) - T ( x ^ {2} ) }{2}. |
| − | \frac{T ^ {2} ( x) - T ( x ^ {2} ) }{2} | ||
| − | |||
$$ | $$ | ||
| − | The functional equations for | + | The functional equations for $T(x)$ and $t(x)$ yield the values of $T_{n}$ |
| − | and | + | and $t_{n}$ for specific values of $n$, see {{Cite|R1}}. |
| − | yield the values of | ||
| − | and | ||
| − | for specific values of | ||
| − | see | ||
It has been shown that, as $ n \rightarrow \infty $, | It has been shown that, as $ n \rightarrow \infty $, | ||
| Line 69: | Line 67: | ||
where $ C = 0.534948 \dots $, | where $ C = 0.534948 \dots $, | ||
| − | $ \alpha = 2.95576 \dots $ | + | $ \alpha = 2.95576 \dots$ (see {{Cite|R2}}). |
| + | |||
| + | Problems of enumeration of trees of a specific kind arise, for example, in chemistry in the study of isomers. | ||
| + | |||
| + | == Encoding == | ||
Trees may be fairly simply coded by strings of zeros and ones. Consider, for example, some regular (without intersection of edges) imbedding of a tree $ D $ | Trees may be fairly simply coded by strings of zeros and ones. Consider, for example, some regular (without intersection of edges) imbedding of a tree $ D $ | ||
| Line 79: | Line 81: | ||
itself, but also its imbedding in the plane. Several different codes correspond to one specific tree. The following estimate follows from this mode of coding: $ t _ {n} < T _ {n} < 4 ^ {n} $. | itself, but also its imbedding in the plane. Several different codes correspond to one specific tree. The following estimate follows from this mode of coding: $ t _ {n} < T _ {n} < 4 ^ {n} $. | ||
| − | A tree | + | A tree $G$ with $n$ |
| − | with | ||
vertices can be uniquely retrieved (up to an isomorphism) from the set of all its $ ( n - 1 ) $- | vertices can be uniquely retrieved (up to an isomorphism) from the set of all its $ ( n - 1 ) $- | ||
vertex subgraphs $ G - v $, | vertex subgraphs $ G - v $, | ||
| Line 88: | Line 89: | ||
Any tree is also uniquely defined by the distances (length of the shortest path) between its terminal (valency 1) vertices. | Any tree is also uniquely defined by the distances (length of the shortest path) between its terminal (valency 1) vertices. | ||
| − | A spanning tree of a graph is a subgraph of the given graph which contains all its vertices and which is a tree. The number of spanning trees of any given connected graph $ | + | == Spanning trees == |
| + | |||
| + | A '''spanning tree''' of a graph is a subgraph of the given graph which contains all its vertices and which is a tree. The number of spanning trees of any given connected graph $G$ | ||
without loops and without multiple edges can be computed as follows. Let $ M $ | without loops and without multiple edges can be computed as follows. Let $ M $ | ||
| − | be the matrix obtained from the [[adjacency matrix]] of $ | + | be the matrix obtained from the [[adjacency matrix]] of $G$ |
by replacing all the signs of the elements by the opposite signs and by replacing the $ i $- | by replacing all the signs of the elements by the opposite signs and by replacing the $ i $- | ||
th entry on the principal diagonal by the valency of the vertex $ v _ {i} $. | th entry on the principal diagonal by the valency of the vertex $ v _ {i} $. | ||
| Line 97: | Line 100: | ||
Spanning trees are employed, for example, to find independent cycles in an electric circuit. | Spanning trees are employed, for example, to find independent cycles in an electric circuit. | ||
| − | Of importance in applications is the problem of finding the spanning tree with the smallest sum of the edge-weights in a connected graph in which weights are assigned to the edges. Such a problem arises, for example, in designing communication networks. An algorithm for the solution of this shortest spanning tree problem is known | + | Of importance in applications is the problem of finding the spanning tree with the smallest sum of the edge-weights in a connected graph in which weights are assigned to the edges. Such a problem arises, for example, in designing communication networks. An [[algorithm]] for the solution of this shortest spanning tree problem is known ({{Cite|R3}}, {{Cite|R4}}). |
| + | |||
| + | == Directed trees == | ||
| + | |||
| + | A tree growing (or issuing) from a vertex $ v _ {0} $ | ||
is the name given to an oriented graph which is (disregarding the orientation) a rooted tree with root $ v _ {0} $, | is the name given to an oriented graph which is (disregarding the orientation) a rooted tree with root $ v _ {0} $, | ||
and in which for any vertex $ v _ {1} $ | and in which for any vertex $ v _ {1} $ | ||
| Line 106: | Line 113: | ||
Such trees are employed, for example, in the description of deterministic functions, for the representation of information in information-searching systems, etc. | Such trees are employed, for example, in the description of deterministic functions, for the representation of information in information-searching systems, etc. | ||
| − | + | == Comments == | |
| − | + | A directed tree is a directed graph which is a tree with root $ r $ such that for each vertex $ v $ | |
| − | + | there is a directed path from $ r $ to $ v $. | |
| + | Thus, each vertex except $ r $ has incoming degree precisely $ 1 $ and $ r $ has incoming degree $ 0 $ | ||
| + | and is a source. Alternatively and equivalently (orientation reversal), a directed tree is a tree with root $ r $ | ||
| + | such that each vertex has outgoing degree $ 1 $ (and $ r $ | ||
| + | has outgoing degree $ 0 $ and is a sink). Both definitions occur in the literature. Sometimes the phrase rooted tree is used in the meaning of directed tree. | ||
| − | == | + | == References == |
| − | + | ||
| − | + | * {{Ref|R1}} F. Harary, "Graph theory", Addison-Wesley (1969) Chapt. 9 {{ZBL|0182.57702}} | |
| − | + | * {{Ref|R2}} R. Otter, "The number of trees", ''Ann. of Math.'', '''49''' : 3 (1948) pp. 583–599 {{ZBL|0032.12601}} | |
| − | + | * {{Ref|R3}} R.C. Prim, "Shortest connection networks and some generalizations", ''Bell Systems Techn. J.'', '''36''' : 6 (1957) pp. 1389–1401 | |
| − | + | * {{Ref|R4}} J.B. Kruskal, "On the shortest spanning subtree of a graph and the travelling salesman problem", ''Proc. Amer. Math. Soc.'', '''7''' (1956) pp. 48–50 | |
| − | + | * {{Ref|a1}} W.K. Chen, "Applied graph theory", North-Holland (1971) | |
| − | and | + | * {{Ref|a2}} L. Comtet, "Advanced combinatorics", Reidel (1974) (Translated from French) |
| − | + | * {{Ref|a3}} M. Goudran, M. Minoux, "Graphes et algorithmes", Eyrolles (1979) Chapt. 4 | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | [[Category:Graph theory]] | |
| − | |||
Latest revision as of 06:20, 30 March 2023
in graph theory
A connected non-oriented graph $G$ which does not contain cycles. A tree has no multiple edges and no loops. Since they are the simplest possible connected graphs, trees are suitable models for the study of various problems in graph theory. Any tree with $n$ vertices contains $n - 1$ edges. The number of different trees which may be constructed on $n$ numbered vertices is $n^{n-2}$.
A tree with one distinguished vertex is said to be a rooted tree. A forest is a graph without cycles: every connected component of a forest is a tree.
Enumeration
The enumerating series
$$ T ( x) = \sum _ {n = 1 } ^ \infty T _ {n} x ^ {n} $$
for the number $ T _ {n} $ of non-isomorphic rooted trees with $ n $ vertices satisfies the functional equation
$$ T ( x) = x \mathop{\rm exp} \sum _ {r = 1 } ^ \infty \frac{1}{r} T ( x ^ {r} ) . $$
The enumerating series
$$ t ( x) = \sum _ {n = 1 } ^ \infty t _ {n} x ^ {n} $$
for the number $ t _ {n} $ of non-isomorphic trees with $ n $ vertices can be represented using the enumerating series for rooted trees:
$$ t ( x) = T ( x) - \frac{T ^ {2} ( x) - T ( x ^ {2} ) }{2}. $$
The functional equations for $T(x)$ and $t(x)$ yield the values of $T_{n}$ and $t_{n}$ for specific values of $n$, see [R1].
It has been shown that, as $ n \rightarrow \infty $,
$$ t _ {n} \sim C \frac{\alpha ^ {n} }{n ^ {5/2} } , $$
where $ C = 0.534948 \dots $, $ \alpha = 2.95576 \dots$ (see [R2]).
Problems of enumeration of trees of a specific kind arise, for example, in chemistry in the study of isomers.
Encoding
Trees may be fairly simply coded by strings of zeros and ones. Consider, for example, some regular (without intersection of edges) imbedding of a tree $ D $ in the plane (cf. Graph imbedding). Starting from any vertex, one moves along the edges of $ D $, turning at each vertex towards the first edge on the right, and returning in the terminal vertices of the tree. While moving along some edge, one writes 0 if the edge is traversed for the first time, and writes 1 when the edge is traversed for the second time (in the opposite direction). If $ m $ is the number of tree edges, one returns to the starting vertex after $ 2m $ steps, having passed each edge twice. The sequence of 0's and 1's of length $ 2m $ thus obtained (the code of the tree) makes it possible to uniquely reconstruct not only the tree $ D $ itself, but also its imbedding in the plane. Several different codes correspond to one specific tree. The following estimate follows from this mode of coding: $ t _ {n} < T _ {n} < 4 ^ {n} $.
A tree $G$ with $n$ vertices can be uniquely retrieved (up to an isomorphism) from the set of all its $ ( n - 1 ) $- vertex subgraphs $ G - v $, which are obtained from $ G $ by elimination of one of its vertices $ v $.
Any tree is also uniquely defined by the distances (length of the shortest path) between its terminal (valency 1) vertices.
Spanning trees
A spanning tree of a graph is a subgraph of the given graph which contains all its vertices and which is a tree. The number of spanning trees of any given connected graph $G$ without loops and without multiple edges can be computed as follows. Let $ M $ be the matrix obtained from the adjacency matrix of $G$ by replacing all the signs of the elements by the opposite signs and by replacing the $ i $- th entry on the principal diagonal by the valency of the vertex $ v _ {i} $. The cofactors of all entries on the principal diagonal of $ M $ will then all be equal, and their common value is the number of spanning trees of $ G $. Spanning trees are employed, for example, to find independent cycles in an electric circuit.
Of importance in applications is the problem of finding the spanning tree with the smallest sum of the edge-weights in a connected graph in which weights are assigned to the edges. Such a problem arises, for example, in designing communication networks. An algorithm for the solution of this shortest spanning tree problem is known ([R3], [R4]).
Directed trees
A tree growing (or issuing) from a vertex $ v _ {0} $ is the name given to an oriented graph which is (disregarding the orientation) a rooted tree with root $ v _ {0} $, and in which for any vertex $ v _ {1} $ the (unique) chain connecting $ v _ {0} $ to $ v _ {1} $ is an oriented path from $ v _ {0} $ to $ v _ {1} $. Such trees are employed, for example, in the description of deterministic functions, for the representation of information in information-searching systems, etc.
Comments
A directed tree is a directed graph which is a tree with root $ r $ such that for each vertex $ v $ there is a directed path from $ r $ to $ v $. Thus, each vertex except $ r $ has incoming degree precisely $ 1 $ and $ r $ has incoming degree $ 0 $ and is a source. Alternatively and equivalently (orientation reversal), a directed tree is a tree with root $ r $ such that each vertex has outgoing degree $ 1 $ (and $ r $ has outgoing degree $ 0 $ and is a sink). Both definitions occur in the literature. Sometimes the phrase rooted tree is used in the meaning of directed tree.
References
- [R1] F. Harary, "Graph theory", Addison-Wesley (1969) Chapt. 9 Zbl 0182.57702
- [R2] R. Otter, "The number of trees", Ann. of Math., 49 : 3 (1948) pp. 583–599 Zbl 0032.12601
- [R3] R.C. Prim, "Shortest connection networks and some generalizations", Bell Systems Techn. J., 36 : 6 (1957) pp. 1389–1401
- [R4] J.B. Kruskal, "On the shortest spanning subtree of a graph and the travelling salesman problem", Proc. Amer. Math. Soc., 7 (1956) pp. 48–50
- [a1] W.K. Chen, "Applied graph theory", North-Holland (1971)
- [a2] L. Comtet, "Advanced combinatorics", Reidel (1974) (Translated from French)
- [a3] M. Goudran, M. Minoux, "Graphes et algorithmes", Eyrolles (1979) Chapt. 4
Tree. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Tree&oldid=51592