Difference between revisions of "Nehari extension problem"
Ulf Rehmann (talk | contribs) m (Undo revision 47954 by Ulf Rehmann (talk)) Tag: Undo |
Ulf Rehmann (talk | contribs) m (tex encoded by computer) |
||
| Line 1: | Line 1: | ||
| − | + | <!-- | |
| + | n1100101.png | ||
| + | $#A+1 = 54 n = 4 | ||
| + | $#C+1 = 54 : ~/encyclopedia/old_files/data/N110/N.1100010 Nehari extension problem | ||
| + | Automatically converted into TeX, above some diagnostics. | ||
| + | Please remove this comment and the {{TEX|auto}} line below, | ||
| + | if TeX found to be correct. | ||
| + | --> | ||
| − | + | {{TEX|auto}} | |
| + | {{TEX|done}} | ||
| − | ii) the norm constraint | + | Let $ \varphi _ {0} , \varphi _ {- 1 } , \varphi _ {- 2 } , \dots $ |
| + | be a given sequence of complex numbers. The Nehari extension problem is the problem to find (if possible) all $ f \in L _ \infty ( \mathbf T ) $ | ||
| + | satisfying the following conditions: | ||
| + | |||
| + | i) the $ n $ | ||
| + | th Fourier coefficient $ c _ {n} ( f ) $ | ||
| + | of $ f $ | ||
| + | is equal to $ \varphi _ {n} $ | ||
| + | for each $ n \leq 0 $; | ||
| + | |||
| + | ii) the norm constraint $ \| f \| _ \infty \leq 1 $ | ||
| + | holds true. Here, $ \| f \| _ \infty $ | ||
| + | is the norm of $ f $ | ||
| + | as an element of the Lebesgue function space $ L _ \infty ( \mathbf T ) $ | ||
| + | and $ \mathbf T $ | ||
| + | is the unit circle. Instead of condition ii) one may require $ \| f \| _ \infty < 1 $, | ||
| + | and in the latter case one calls the problem suboptimal. | ||
The Nehari extension problem is not always solvable. In fact (see [[#References|[a12]]]), the problem has a solution if and only if the infinite [[Hankel matrix]] | The Nehari extension problem is not always solvable. In fact (see [[#References|[a12]]]), the problem has a solution if and only if the infinite [[Hankel matrix]] | ||
| − | < | + | $$ |
| + | \left ( | ||
| + | |||
| + | \begin{array}{cccc} | ||
| + | \varphi _ {0} &\varphi _ {- 1 } &\varphi _ {- 1 } &\cdot \\ | ||
| + | \varphi _ {- 1 } &\varphi _ {- 2 } &\varphi _ {- 3 } &\cdot \\ | ||
| + | \varphi _ {- 2 } &\varphi _ {- 3 } &\varphi _ {- 4 } &\cdot \\ | ||
| + | \cdot &\cdot &\cdot &\cdot \\ | ||
| + | \end{array} | ||
| + | |||
| + | \right ) | ||
| + | $$ | ||
| + | |||
| + | induces a bounded [[Linear operator|linear operator]] $ \Phi $ | ||
| + | on $ {\mathcal l} ^ {2} $, | ||
| + | the [[Hilbert space|Hilbert space]] of all square-summable sequences, such that its operator norm is at most one, i.e., $ \| \Phi \| \leq 1 $. | ||
| + | The suboptimal version of the problem is solvable if and only if $ \| \Phi \| < 1 $. | ||
| + | If $ \| \Phi \| = 1 $, | ||
| + | either the solution of the Nehari extension problem is unique or there are infinitely many solutions. If $ \| \Phi \| < 1 $, | ||
| + | then the problem and its suboptimal version always have infinitely many solutions, which can be parametrized by a fractional-linear mapping. | ||
| + | |||
| + | For the suboptimal case, the set of all solutions $ f $ | ||
| + | in the Wiener algebra $ {\mathcal W} $, | ||
| + | i.e., when one requires additionally that $ \sum _ {n = - \infty } ^ \infty | {c _ {n} ( f ) } | < \infty $, | ||
| + | can be described as follows. In this case, it is assumed that the given sequence $ \varphi _ {0} , \varphi _ {- 1 } , \varphi _ {- 2 } , \dots $ | ||
| + | is absolutely summable. Let $ \| \Phi \| < 1 $. | ||
| + | Then the operators $ I - \Phi ^ {*} \Phi $ | ||
| + | and $ I - \Phi \Phi ^ {*} $ | ||
| + | are boundedly invertible on $ {\mathcal l} ^ {2} $, | ||
| + | and one can build the following infinite column vectors: | ||
| + | |||
| + | $$ | ||
| + | \left ( | ||
| + | |||
| + | \begin{array}{c} | ||
| + | a _ {0} \\ | ||
| + | a _ {- 1 } \\ | ||
| + | a _ {- 2 } \\ | ||
| + | \vdots \\ | ||
| + | \end{array} | ||
| + | |||
| + | \right ) = ( I - \Phi \Phi ^ {*} ) ^ {- 1 } \left ( | ||
| + | |||
| + | \begin{array}{c} | ||
| + | 1 \\ | ||
| + | 0 \\ | ||
| + | 0 \\ | ||
| + | \vdots \\ | ||
| + | \end{array} | ||
| + | |||
| + | \right ) , | ||
| + | $$ | ||
| + | |||
| + | $$ | ||
| + | \left ( | ||
| + | |||
| + | \begin{array}{c} | ||
| + | c _ {0} \\ | ||
| + | c _ {1} \\ | ||
| + | c _ {2} \\ | ||
| + | \vdots \\ | ||
| + | \end{array} | ||
| + | |||
| + | \right ) = \Phi ^ {*} \left ( | ||
| + | |||
| + | \begin{array}{c} | ||
| + | a _ {0} \\ | ||
| + | a _ {- 1 } \\ | ||
| + | a _ {- 2 } \\ | ||
| + | \vdots \\ | ||
| + | \end{array} | ||
| − | + | \right ) , \left ( | |
| − | + | \begin{array}{c} | |
| + | d _ {0} \\ | ||
| + | d _ {1} \\ | ||
| + | d _ {2} \\ | ||
| + | \vdots \\ | ||
| + | \end{array} | ||
| − | + | \right ) = ( I - \Phi ^ {*} \Phi ) ^ {- 1 } \left ( | |
| − | + | \begin{array}{c} | |
| + | 1 \\ | ||
| + | 0 \\ | ||
| + | 0 \\ | ||
| + | \vdots \\ | ||
| + | \end{array} | ||
| − | + | \right ) , | |
| + | $$ | ||
| + | |||
| + | $$ | ||
| + | \left ( | ||
| + | |||
| + | \begin{array}{c} | ||
| + | b _ {0} \\ | ||
| + | b _ {- 1 } \\ | ||
| + | b _ {- 2 } \\ | ||
| + | \vdots \\ | ||
| + | \end{array} | ||
| + | |||
| + | \right ) = \Phi \left ( | ||
| + | |||
| + | \begin{array}{c} | ||
| + | d _ {0} \\ | ||
| + | d _ {1} \\ | ||
| + | d _ {2} \\ | ||
| + | \vdots \\ | ||
| + | \end{array} | ||
| + | |||
| + | \right ) . | ||
| + | $$ | ||
Now, consider the functions | Now, consider the functions | ||
| − | + | $$ | |
| + | \alpha ( \lambda ) = \sum _ {j = - \infty } ^ { 0 } a _ {j} a _ {0} ^ {- {1 / 2 } } \lambda ^ {j} , | ||
| + | $$ | ||
| − | + | $$ | |
| + | \gamma ( \lambda ) = \sum _ {j = 0 } ^ \infty c _ {j} a _ {0} ^ {- {1 / 2 } } \lambda ^ {j} , \delta ( \lambda ) = \sum _ {j = 0 } ^ \infty d _ {j} d _ {0} ^ {- {1 / 2 } } \lambda ^ {j} , | ||
| + | $$ | ||
| − | + | $$ | |
| + | \beta ( \lambda ) = \sum _ {j = - \infty } ^ { 0 } b _ {j} b _ {0} ^ {- {1 / 2 } } \lambda ^ {j} . | ||
| + | $$ | ||
| − | Then, each solution | + | Then, each solution $ f \in {\mathcal W} $ |
| + | of the suboptimal Nehari extension problem for the sequence $ \varphi _ {0} , \varphi _ {- 1 } , \varphi _ {- 2 } , \dots $ | ||
| + | is of the form | ||
| − | + | $$ \tag{a1 } | |
| + | f ( \lambda ) = ( \alpha ( \lambda ) h ( \lambda ) + \beta ( \lambda ) ) ( \gamma ( \lambda ) h ( \lambda ) + \delta ( \lambda ) ) ^ {- 1 } , | ||
| + | $$ | ||
| − | where | + | where $ \lambda \in \mathbf T $ |
| + | and $ h $ | ||
| + | is an arbitrary element of the Wiener algebra $ {\mathcal W} $ | ||
| + | such that $ | {h ( \lambda ) } | < 1 $ | ||
| + | for $ \lambda \in \mathbf T $ | ||
| + | and the $ n $ | ||
| + | th Fourier coefficient of $ h $ | ||
| + | is zero for each $ n \leq 0 $. | ||
| + | Moreover, (a1) gives a one-to-one correspondence between all such $ h $ | ||
| + | and all solutions $ f $. | ||
| + | The central solution, i.e., the solution $ f _ {\textrm{ cen } } ( \lambda ) = \beta ( \lambda ) \delta ( \lambda ) ^ {- 1 } $, | ||
| + | which one obtains when the free parameter $ h $ | ||
| + | in (a1) is identically zero, has a maximum entropy characterization. In fact, it is the unique solution $ f \in {\mathcal W} $ | ||
| + | of the suboptimal Nehari extension problem that maximizes the entropy integral | ||
| − | + | $$ | |
| + | { | ||
| + | \frac{1}{2 \pi } | ||
| + | } \int\limits _ {- \pi } ^ \pi { { \mathop{\rm log} } ( 1 - \left | {f ( e ^ {it } ) } \right | ^ {2} ) } {dt } . | ||
| + | $$ | ||
| − | The Nehari extension problem has natural generalizations for matrix-valued and operator-valued functions, and it has two-block and four-block analogues. In the matrix-valued case, a superoptimal Nehari extension problem is studied also. In the latter problem the constraint is made not only for the norm, but also for a number of first singular values [[#References|[a13]]]. There exist many different approaches to treat the Nehari problem and its various generalizations. For instance, the method of one-step extensions (see [[#References|[a1]]]), the commutant-lifting approach (see [[#References|[a6]]] and [[Commutant lifting theorem|Commutant lifting theorem]]), the [[Band method|band method]] (see [[#References|[a10]]]), reproducing-kernel Hilbert space techniques (see [[#References|[a5]]]), and Beurling–Lax methods in Krein spaces (see [[#References|[a4]]] and [[Krein space|Krein space]]). The results are used in [[H^infinity-control-theory| | + | The Nehari extension problem has natural generalizations for matrix-valued and operator-valued functions, and it has two-block and four-block analogues. In the matrix-valued case, a superoptimal Nehari extension problem is studied also. In the latter problem the constraint is made not only for the norm, but also for a number of first singular values [[#References|[a13]]]. There exist many different approaches to treat the Nehari problem and its various generalizations. For instance, the method of one-step extensions (see [[#References|[a1]]]), the commutant-lifting approach (see [[#References|[a6]]] and [[Commutant lifting theorem|Commutant lifting theorem]]), the [[Band method|band method]] (see [[#References|[a10]]]), reproducing-kernel Hilbert space techniques (see [[#References|[a5]]]), and Beurling–Lax methods in Krein spaces (see [[#References|[a4]]] and [[Krein space|Krein space]]). The results are used in [[H^infinity-control-theory| $ H ^ \infty $ |
| + | control theory]] (see [[#References|[a8]]]), and when the data are Fourier coefficients of a rational matrix function, the formulas for the coefficients in the linear fractional representation (a1) can be represented explicitly in state-space form (see [[#References|[a9]]] and [[#References|[a3]]]). | ||
The Nehari extension problem also has non-stationary versions, in which the role of analytic functions is taken over by lower-triangular matrices. An example is the problem to complete a given lower-triangular array of numbers, | The Nehari extension problem also has non-stationary versions, in which the role of analytic functions is taken over by lower-triangular matrices. An example is the problem to complete a given lower-triangular array of numbers, | ||
| − | + | $$ | |
| + | \left ( | ||
| + | |||
| + | \begin{array}{cccc} | ||
| + | \varphi _ {00 } &{} &{} &{} \\ | ||
| + | \varphi _ {10 } &\varphi _ {11 } &{} &{} \\ | ||
| + | \varphi _ {20 } &\varphi _ {21 } &\varphi _ {22 } &{} \\ | ||
| + | \cdot &\cdot &\cdot &\cdot \\ | ||
| + | \end{array} | ||
| + | |||
| + | \right ) , | ||
| + | $$ | ||
| − | to a full infinite matrix such that the resulting operator on | + | to a full infinite matrix such that the resulting operator on $ {\mathcal l} ^ {2} $ |
| + | is bounded and has operator norm at most one. The non-stationary variants of the Nehari extension problem have been treated in terms of nest algebras [[#References|[a2]]]. The main results for the stationary case carry over to the non-stationary case [[#References|[a11]]], [[#References|[a7]]]. | ||
====References==== | ====References==== | ||
<table><TR><TD valign="top">[a1]</TD> <TD valign="top"> V.M. Adamjan, D.Z. Arov, M.G. Krein, "Infinite Hankel block matrices and related extension problems" ''Transl. Amer. Math. Soc.'' , '''111''' (1978) pp. 133–156 ''Izv. Akad. Nauk SSSR Ser. Mat.'' , '''6''' (1971) pp. 87–112</TD></TR><TR><TD valign="top">[a2]</TD> <TD valign="top"> W.B. Arveson, "Interpolation in nest algebras" ''J. Funct. Anal.'' , '''20''' (1975) pp. 208–233</TD></TR><TR><TD valign="top">[a3]</TD> <TD valign="top"> J. Ball, I. Gohberg, L. Rodman, "Interpolation of rational matrix functions" , ''Operator Theory: Advances and Applications'' , '''45''' , Birkhäuser (1990)</TD></TR><TR><TD valign="top">[a4]</TD> <TD valign="top"> J. Ball, J.W. Helton, "A Beurling–Lax theorem for Lie group <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/n/n110/n110010/n11001055.png" /> which contains classical interpolation theory" ''J. Operator Th.'' , '''9''' (1983) pp. 107–142</TD></TR><TR><TD valign="top">[a5]</TD> <TD valign="top"> H. Dym, "<img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/n/n110/n110010/n11001056.png" /> contractive matrix functions, reproducing kernel Hilbert spaces and interpolation" , ''CBMS'' , '''71''' , Amer. Math. Soc. (1989)</TD></TR><TR><TD valign="top">[a6]</TD> <TD valign="top"> C. Foias, A.E. Frazho, "The commutant lifting approach to interpolation problems" , ''Operator Theory: Advances and Applications'' , '''44''' , Birkhäuser (1990)</TD></TR><TR><TD valign="top">[a7]</TD> <TD valign="top"> C. Foias, A.E. Frazho, I. Gohberg, M.A. Kaashoek, "Discrete time-variant interpolation as classical interpolation with an operator argument" ''Integral Eq. Operator Th.'' , '''26''' (1996) pp. 371–403</TD></TR><TR><TD valign="top">[a8]</TD> <TD valign="top"> B.A. Francis, "A course in <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/n/n110/n110010/n11001057.png" /> control theory" , Springer (1987)</TD></TR><TR><TD valign="top">[a9]</TD> <TD valign="top"> K. Glover, "All optimal Hankel-norm approximations of linear multivariable systems and the <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/n/n110/n110010/n11001058.png" />-error bounds" ''Int. J. Control'' , '''39''' (1984) pp. 1115–1193</TD></TR><TR><TD valign="top">[a10]</TD> <TD valign="top"> I. Gohberg, S. Goldberg, M.A Kaashoek, "Classes of linear operators II" , ''Operator Theory: Advances and Applications'' , '''63''' , Birkhäuser (1993)</TD></TR><TR><TD valign="top">[a11]</TD> <TD valign="top"> I. Gohberg, M.A. Kaashoek, H.J. Woerdeman, "The band method for positive and contractive extension problems: An alternative version and new applications" ''Integral Eq. Operator Th.'' , '''12''' (1989) pp. 343–382</TD></TR><TR><TD valign="top">[a12]</TD> <TD valign="top"> Z. Nehari, "On bounded bilinear forms" ''Ann. of Math.'' , '''65''' (1957) pp. 153–162</TD></TR><TR><TD valign="top">[a13]</TD> <TD valign="top"> V.V. Peller, N.J. Young, "Superoptimal analytic approximations of matrix functions" ''J. Funct. Anal.'' , '''120''' (1994) pp. 300–343</TD></TR></table> | <table><TR><TD valign="top">[a1]</TD> <TD valign="top"> V.M. Adamjan, D.Z. Arov, M.G. Krein, "Infinite Hankel block matrices and related extension problems" ''Transl. Amer. Math. Soc.'' , '''111''' (1978) pp. 133–156 ''Izv. Akad. Nauk SSSR Ser. Mat.'' , '''6''' (1971) pp. 87–112</TD></TR><TR><TD valign="top">[a2]</TD> <TD valign="top"> W.B. Arveson, "Interpolation in nest algebras" ''J. Funct. Anal.'' , '''20''' (1975) pp. 208–233</TD></TR><TR><TD valign="top">[a3]</TD> <TD valign="top"> J. Ball, I. Gohberg, L. Rodman, "Interpolation of rational matrix functions" , ''Operator Theory: Advances and Applications'' , '''45''' , Birkhäuser (1990)</TD></TR><TR><TD valign="top">[a4]</TD> <TD valign="top"> J. Ball, J.W. Helton, "A Beurling–Lax theorem for Lie group <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/n/n110/n110010/n11001055.png" /> which contains classical interpolation theory" ''J. Operator Th.'' , '''9''' (1983) pp. 107–142</TD></TR><TR><TD valign="top">[a5]</TD> <TD valign="top"> H. Dym, "<img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/n/n110/n110010/n11001056.png" /> contractive matrix functions, reproducing kernel Hilbert spaces and interpolation" , ''CBMS'' , '''71''' , Amer. Math. Soc. (1989)</TD></TR><TR><TD valign="top">[a6]</TD> <TD valign="top"> C. Foias, A.E. Frazho, "The commutant lifting approach to interpolation problems" , ''Operator Theory: Advances and Applications'' , '''44''' , Birkhäuser (1990)</TD></TR><TR><TD valign="top">[a7]</TD> <TD valign="top"> C. Foias, A.E. Frazho, I. Gohberg, M.A. Kaashoek, "Discrete time-variant interpolation as classical interpolation with an operator argument" ''Integral Eq. Operator Th.'' , '''26''' (1996) pp. 371–403</TD></TR><TR><TD valign="top">[a8]</TD> <TD valign="top"> B.A. Francis, "A course in <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/n/n110/n110010/n11001057.png" /> control theory" , Springer (1987)</TD></TR><TR><TD valign="top">[a9]</TD> <TD valign="top"> K. Glover, "All optimal Hankel-norm approximations of linear multivariable systems and the <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/n/n110/n110010/n11001058.png" />-error bounds" ''Int. J. Control'' , '''39''' (1984) pp. 1115–1193</TD></TR><TR><TD valign="top">[a10]</TD> <TD valign="top"> I. Gohberg, S. Goldberg, M.A Kaashoek, "Classes of linear operators II" , ''Operator Theory: Advances and Applications'' , '''63''' , Birkhäuser (1993)</TD></TR><TR><TD valign="top">[a11]</TD> <TD valign="top"> I. Gohberg, M.A. Kaashoek, H.J. Woerdeman, "The band method for positive and contractive extension problems: An alternative version and new applications" ''Integral Eq. Operator Th.'' , '''12''' (1989) pp. 343–382</TD></TR><TR><TD valign="top">[a12]</TD> <TD valign="top"> Z. Nehari, "On bounded bilinear forms" ''Ann. of Math.'' , '''65''' (1957) pp. 153–162</TD></TR><TR><TD valign="top">[a13]</TD> <TD valign="top"> V.V. Peller, N.J. Young, "Superoptimal analytic approximations of matrix functions" ''J. Funct. Anal.'' , '''120''' (1994) pp. 300–343</TD></TR></table> | ||
Latest revision as of 14:32, 7 June 2020
Let $ \varphi _ {0} , \varphi _ {- 1 } , \varphi _ {- 2 } , \dots $
be a given sequence of complex numbers. The Nehari extension problem is the problem to find (if possible) all $ f \in L _ \infty ( \mathbf T ) $
satisfying the following conditions:
i) the $ n $ th Fourier coefficient $ c _ {n} ( f ) $ of $ f $ is equal to $ \varphi _ {n} $ for each $ n \leq 0 $;
ii) the norm constraint $ \| f \| _ \infty \leq 1 $ holds true. Here, $ \| f \| _ \infty $ is the norm of $ f $ as an element of the Lebesgue function space $ L _ \infty ( \mathbf T ) $ and $ \mathbf T $ is the unit circle. Instead of condition ii) one may require $ \| f \| _ \infty < 1 $, and in the latter case one calls the problem suboptimal.
The Nehari extension problem is not always solvable. In fact (see [a12]), the problem has a solution if and only if the infinite Hankel matrix
$$ \left ( \begin{array}{cccc} \varphi _ {0} &\varphi _ {- 1 } &\varphi _ {- 1 } &\cdot \\ \varphi _ {- 1 } &\varphi _ {- 2 } &\varphi _ {- 3 } &\cdot \\ \varphi _ {- 2 } &\varphi _ {- 3 } &\varphi _ {- 4 } &\cdot \\ \cdot &\cdot &\cdot &\cdot \\ \end{array} \right ) $$
induces a bounded linear operator $ \Phi $ on $ {\mathcal l} ^ {2} $, the Hilbert space of all square-summable sequences, such that its operator norm is at most one, i.e., $ \| \Phi \| \leq 1 $. The suboptimal version of the problem is solvable if and only if $ \| \Phi \| < 1 $. If $ \| \Phi \| = 1 $, either the solution of the Nehari extension problem is unique or there are infinitely many solutions. If $ \| \Phi \| < 1 $, then the problem and its suboptimal version always have infinitely many solutions, which can be parametrized by a fractional-linear mapping.
For the suboptimal case, the set of all solutions $ f $ in the Wiener algebra $ {\mathcal W} $, i.e., when one requires additionally that $ \sum _ {n = - \infty } ^ \infty | {c _ {n} ( f ) } | < \infty $, can be described as follows. In this case, it is assumed that the given sequence $ \varphi _ {0} , \varphi _ {- 1 } , \varphi _ {- 2 } , \dots $ is absolutely summable. Let $ \| \Phi \| < 1 $. Then the operators $ I - \Phi ^ {*} \Phi $ and $ I - \Phi \Phi ^ {*} $ are boundedly invertible on $ {\mathcal l} ^ {2} $, and one can build the following infinite column vectors:
$$ \left ( \begin{array}{c} a _ {0} \\ a _ {- 1 } \\ a _ {- 2 } \\ \vdots \\ \end{array} \right ) = ( I - \Phi \Phi ^ {*} ) ^ {- 1 } \left ( \begin{array}{c} 1 \\ 0 \\ 0 \\ \vdots \\ \end{array} \right ) , $$
$$ \left ( \begin{array}{c} c _ {0} \\ c _ {1} \\ c _ {2} \\ \vdots \\ \end{array} \right ) = \Phi ^ {*} \left ( \begin{array}{c} a _ {0} \\ a _ {- 1 } \\ a _ {- 2 } \\ \vdots \\ \end{array} \right ) , \left ( \begin{array}{c} d _ {0} \\ d _ {1} \\ d _ {2} \\ \vdots \\ \end{array} \right ) = ( I - \Phi ^ {*} \Phi ) ^ {- 1 } \left ( \begin{array}{c} 1 \\ 0 \\ 0 \\ \vdots \\ \end{array} \right ) , $$
$$ \left ( \begin{array}{c} b _ {0} \\ b _ {- 1 } \\ b _ {- 2 } \\ \vdots \\ \end{array} \right ) = \Phi \left ( \begin{array}{c} d _ {0} \\ d _ {1} \\ d _ {2} \\ \vdots \\ \end{array} \right ) . $$
Now, consider the functions
$$ \alpha ( \lambda ) = \sum _ {j = - \infty } ^ { 0 } a _ {j} a _ {0} ^ {- {1 / 2 } } \lambda ^ {j} , $$
$$ \gamma ( \lambda ) = \sum _ {j = 0 } ^ \infty c _ {j} a _ {0} ^ {- {1 / 2 } } \lambda ^ {j} , \delta ( \lambda ) = \sum _ {j = 0 } ^ \infty d _ {j} d _ {0} ^ {- {1 / 2 } } \lambda ^ {j} , $$
$$ \beta ( \lambda ) = \sum _ {j = - \infty } ^ { 0 } b _ {j} b _ {0} ^ {- {1 / 2 } } \lambda ^ {j} . $$
Then, each solution $ f \in {\mathcal W} $ of the suboptimal Nehari extension problem for the sequence $ \varphi _ {0} , \varphi _ {- 1 } , \varphi _ {- 2 } , \dots $ is of the form
$$ \tag{a1 } f ( \lambda ) = ( \alpha ( \lambda ) h ( \lambda ) + \beta ( \lambda ) ) ( \gamma ( \lambda ) h ( \lambda ) + \delta ( \lambda ) ) ^ {- 1 } , $$
where $ \lambda \in \mathbf T $ and $ h $ is an arbitrary element of the Wiener algebra $ {\mathcal W} $ such that $ | {h ( \lambda ) } | < 1 $ for $ \lambda \in \mathbf T $ and the $ n $ th Fourier coefficient of $ h $ is zero for each $ n \leq 0 $. Moreover, (a1) gives a one-to-one correspondence between all such $ h $ and all solutions $ f $. The central solution, i.e., the solution $ f _ {\textrm{ cen } } ( \lambda ) = \beta ( \lambda ) \delta ( \lambda ) ^ {- 1 } $, which one obtains when the free parameter $ h $ in (a1) is identically zero, has a maximum entropy characterization. In fact, it is the unique solution $ f \in {\mathcal W} $ of the suboptimal Nehari extension problem that maximizes the entropy integral
$$ { \frac{1}{2 \pi } } \int\limits _ {- \pi } ^ \pi { { \mathop{\rm log} } ( 1 - \left | {f ( e ^ {it } ) } \right | ^ {2} ) } {dt } . $$
The Nehari extension problem has natural generalizations for matrix-valued and operator-valued functions, and it has two-block and four-block analogues. In the matrix-valued case, a superoptimal Nehari extension problem is studied also. In the latter problem the constraint is made not only for the norm, but also for a number of first singular values [a13]. There exist many different approaches to treat the Nehari problem and its various generalizations. For instance, the method of one-step extensions (see [a1]), the commutant-lifting approach (see [a6] and Commutant lifting theorem), the band method (see [a10]), reproducing-kernel Hilbert space techniques (see [a5]), and Beurling–Lax methods in Krein spaces (see [a4] and Krein space). The results are used in $ H ^ \infty $ control theory (see [a8]), and when the data are Fourier coefficients of a rational matrix function, the formulas for the coefficients in the linear fractional representation (a1) can be represented explicitly in state-space form (see [a9] and [a3]).
The Nehari extension problem also has non-stationary versions, in which the role of analytic functions is taken over by lower-triangular matrices. An example is the problem to complete a given lower-triangular array of numbers,
$$ \left ( \begin{array}{cccc} \varphi _ {00 } &{} &{} &{} \\ \varphi _ {10 } &\varphi _ {11 } &{} &{} \\ \varphi _ {20 } &\varphi _ {21 } &\varphi _ {22 } &{} \\ \cdot &\cdot &\cdot &\cdot \\ \end{array} \right ) , $$
to a full infinite matrix such that the resulting operator on $ {\mathcal l} ^ {2} $ is bounded and has operator norm at most one. The non-stationary variants of the Nehari extension problem have been treated in terms of nest algebras [a2]. The main results for the stationary case carry over to the non-stationary case [a11], [a7].
References
| [a1] | V.M. Adamjan, D.Z. Arov, M.G. Krein, "Infinite Hankel block matrices and related extension problems" Transl. Amer. Math. Soc. , 111 (1978) pp. 133–156 Izv. Akad. Nauk SSSR Ser. Mat. , 6 (1971) pp. 87–112 |
| [a2] | W.B. Arveson, "Interpolation in nest algebras" J. Funct. Anal. , 20 (1975) pp. 208–233 |
| [a3] | J. Ball, I. Gohberg, L. Rodman, "Interpolation of rational matrix functions" , Operator Theory: Advances and Applications , 45 , Birkhäuser (1990) |
| [a4] | J. Ball, J.W. Helton, "A Beurling–Lax theorem for Lie group 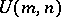 which contains classical interpolation theory" J. Operator Th. , 9 (1983) pp. 107–142 which contains classical interpolation theory" J. Operator Th. , 9 (1983) pp. 107–142 |
| [a5] | H. Dym, "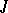 contractive matrix functions, reproducing kernel Hilbert spaces and interpolation" , CBMS , 71 , Amer. Math. Soc. (1989) contractive matrix functions, reproducing kernel Hilbert spaces and interpolation" , CBMS , 71 , Amer. Math. Soc. (1989) |
| [a6] | C. Foias, A.E. Frazho, "The commutant lifting approach to interpolation problems" , Operator Theory: Advances and Applications , 44 , Birkhäuser (1990) |
| [a7] | C. Foias, A.E. Frazho, I. Gohberg, M.A. Kaashoek, "Discrete time-variant interpolation as classical interpolation with an operator argument" Integral Eq. Operator Th. , 26 (1996) pp. 371–403 |
| [a8] | B.A. Francis, "A course in 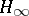 control theory" , Springer (1987) control theory" , Springer (1987) |
| [a9] | K. Glover, "All optimal Hankel-norm approximations of linear multivariable systems and the 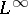 -error bounds" Int. J. Control , 39 (1984) pp. 1115–1193 -error bounds" Int. J. Control , 39 (1984) pp. 1115–1193 |
| [a10] | I. Gohberg, S. Goldberg, M.A Kaashoek, "Classes of linear operators II" , Operator Theory: Advances and Applications , 63 , Birkhäuser (1993) |
| [a11] | I. Gohberg, M.A. Kaashoek, H.J. Woerdeman, "The band method for positive and contractive extension problems: An alternative version and new applications" Integral Eq. Operator Th. , 12 (1989) pp. 343–382 |
| [a12] | Z. Nehari, "On bounded bilinear forms" Ann. of Math. , 65 (1957) pp. 153–162 |
| [a13] | V.V. Peller, N.J. Young, "Superoptimal analytic approximations of matrix functions" J. Funct. Anal. , 120 (1994) pp. 300–343 |
Nehari extension problem. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Nehari_extension_problem&oldid=49318