|
|
| (3 intermediate revisions by 2 users not shown) |
| Line 1: |
Line 1: |
| − | Let <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f130/f130100/f1301001.png" /> be a locally compact group, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f130/f130100/f1301002.png" /> and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f130/f130100/f1301003.png" />. Consider the set <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f130/f130100/f1301004.png" /> of all pairs <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f130/f130100/f1301005.png" />, with <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f130/f130100/f1301006.png" /> a sequence in <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f130/f130100/f1301007.png" /> and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f130/f130100/f1301008.png" /> a sequence in <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f130/f130100/f1301009.png" /> such that <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f130/f130100/f13010010.png" />. Here, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f130/f130100/f13010011.png" /> is defined by <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f130/f130100/f13010012.png" />, where <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f130/f130100/f13010013.png" /> is some left-invariant [[Haar measure|Haar measure]] on <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f130/f130100/f13010014.png" />. Let <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f130/f130100/f13010015.png" /> denote the set of all <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f130/f130100/f13010016.png" /> for which there is a pair <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f130/f130100/f13010017.png" /> such that <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f130/f130100/f13010018.png" />, where <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f130/f130100/f13010019.png" />. The set <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f130/f130100/f13010020.png" /> is a linear subspace of the <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f130/f130100/f13010021.png" />-vector space of all continuous complex-valued functions on <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f130/f130100/f13010022.png" /> vanishing at infinity. For <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f130/f130100/f13010023.png" /> one sets
| + | <!--This article has been texified automatically. Since there was no Nroff source code for this article, |
| | + | the semi-automatic procedure described at https://encyclopediaofmath.org/wiki/User:Maximilian_Janisch/latexlist |
| | + | was used. |
| | + | If the TeX and formula formatting is correct and if all png images have been replaced by TeX code, please remove this message and the {{TEX|semi-auto}} category. |
| | | | |
| − | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f130/f130100/f13010024.png" /></td> </tr></table>
| + | Out of 170 formulas, 166 were replaced by TEX code.--> |
| | | | |
| − | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f130/f130100/f13010025.png" /></td> </tr></table> | + | {{TEX|semi-auto}}{{TEX|part}} |
| | + | Let $G$ be a locally compact group, $1 < p < \infty$ and $p ^ { \prime } = p / p - 1$. Consider the set $\mathcal{A} _ { p } ( G )$ of all pairs $( ( k _ { n } ) _ { n = 1 } ^ { \infty } , ( l _ { n } ) _ { n = 1 } ^ { \infty } )$, with $( k _ { n } ) _ { n = 1 } ^ { \infty }$ a sequence in ${\cal L} _ {\bf C } ^ { p } ( G )$ and $( l _ { n } ) _ { n = 1 } ^ { \infty } $ a sequence in $\mathcal{L} _ { \text{C} } ^ { p ^ { \prime } } ( G )$ such that $\sum _ { n = 1 } ^ { \infty } N _ { p } ( k _ { n } ) N _ { p^{\prime} } ( l _ { n } ) < \infty$. Here, $N _ { p } ( f )$ is defined by $N _ { p } ( f ) = ( \int _ { G } | f ( x ) | ^ { p } d m ( x ) ) ^ { 1 / p }$, where $m$ is some left-invariant [[Haar measure|Haar measure]] on $G$. Let $A _ { p } ( G )$ denote the set of all $u \in {\bf C} ^ { G }$ for which there is a pair $( ( k _ { n } ) _ { n = 1 } ^ { \infty } , ( l _ { n } ) _ { n = 1 } ^ { \infty } ) \in \mathcal{A} _ { p } ( G )$ such that $u ( x ) = \sum _ { n = 1 } ^ { \infty } \overline { k _ { n } } * \check{l} _ { n } ( x )$, where $\check{\varphi} { P } ( x ) = \varphi ( x ^ { - 1 } )$. The set $A _ { p } ( G )$ is a linear subspace of the $\mathbf{C}$-vector space of all continuous complex-valued functions on $G$ vanishing at infinity. For $u \in A _ { p } ( G )$ one sets |
| | | | |
| − | 1) For the pointwise product on <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f130/f130100/f13010026.png" />, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f130/f130100/f13010027.png" /> is a [[Banach algebra|Banach algebra]]. This algebra is called the Figà-Talamanca algebra of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f130/f130100/f13010028.png" />. If <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f130/f130100/f13010029.png" /> is Abelian, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f130/f130100/f13010030.png" /> is isometrically isomorphic to <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f130/f130100/f13010031.png" />, where <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f130/f130100/f13010032.png" /> is the dual group of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f130/f130100/f13010033.png" />. For <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f130/f130100/f13010034.png" /> not necessarily Abelian, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f130/f130100/f13010035.png" /> is precisely the [[Fourier-algebra(2)|Fourier algebra]] of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f130/f130100/f13010036.png" />.
| + | <table class="eq" style="width:100%;"> <tr><td style="width:94%;text-align:center;" valign="top"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f130/f130100/f13010024.png"/></td> </tr></table> |
| | | | |
| − | 2) If <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f130/f130100/f13010037.png" /> is amenable, then <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f130/f130100/f13010038.png" />. The algebra <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f130/f130100/f13010039.png" /> is a useful tool for studying the <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f130/f130100/f13010040.png" />-convolution operators of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f130/f130100/f13010041.png" /> (see [[#References|[a2]]], [[#References|[a7]]], [[#References|[a8]]]). For a function <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f130/f130100/f13010042.png" /> on <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f130/f130100/f13010043.png" /> and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f130/f130100/f13010044.png" /> one sets <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f130/f130100/f13010045.png" />. A continuous [[Linear operator|linear operator]] <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f130/f130100/f13010046.png" /> on <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f130/f130100/f13010047.png" /> is said to be a <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f130/f130100/f13010049.png" />-convolution operator of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f130/f130100/f13010050.png" /> if <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f130/f130100/f13010051.png" /> for every <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f130/f130100/f13010052.png" /> and every <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f130/f130100/f13010053.png" />. Let <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f130/f130100/f13010054.png" /> be the set of all <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f130/f130100/f13010055.png" />-convolution operators of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f130/f130100/f13010056.png" />. It is a closed subalgebra of the Banach algebra <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f130/f130100/f13010057.png" /> of all continuous linear operators on <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f130/f130100/f13010058.png" />. For a complex bounded [[Measure|measure]] <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f130/f130100/f13010059.png" /> on <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f130/f130100/f13010060.png" /> (i.e. <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f130/f130100/f13010061.png" />) and a continuous complex-valued function <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f130/f130100/f13010062.png" /> with compact support on <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f130/f130100/f13010063.png" /> (<img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f130/f130100/f13010064.png" />), the rule <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f130/f130100/f13010065.png" /> defines a <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f130/f130100/f13010066.png" />-convolution operator <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f130/f130100/f13010067.png" />. Of course, for <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f130/f130100/f13010068.png" />, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f130/f130100/f13010069.png" /> denotes the set of all <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f130/f130100/f13010070.png" /> with <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f130/f130100/f13010071.png" /> <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f130/f130100/f13010072.png" />-almost everywhere.
| + | \begin{equation*} \left\{ \sum _ { n = 1 } ^ { \infty } N _ { p } ( k _ { n } ) N _ { p^{\prime} } ( l _ { n } ) : \begin{array} { c c } {((k_n)^{\infty}_{n=1} , (l_n)^{\infty}_{n=1}) \in \mathcal{A}_{p} (G) } \\ {\text { with } u = \sum _ { n = 1 } ^ { \infty } \overline { k _ { n } } * \check{l}_ { n }} \end{array} \right\}. \end{equation*} |
| | | | |
| − | Even for <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f130/f130100/f13010073.png" /> one has <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f130/f130100/f13010074.png" />. Let <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f130/f130100/f13010075.png" /> be the closure in <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f130/f130100/f13010076.png" /> of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f130/f130100/f13010077.png" /> with respect to the ultraweak operator topology on <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f130/f130100/f13010078.png" />.
| + | 1) For the pointwise product on $G$, $A _ { p } ( G )$ is a [[Banach algebra|Banach algebra]]. This algebra is called the Figà-Talamanca algebra of $G$. If $G$ is Abelian, $A _ { 2 } ( G )$ is isometrically isomorphic to $L _ { \text{C} } ^ { 1 } ( \hat { G } )$, where $\hat { C }$ is the dual group of $G$. For $G$ not necessarily Abelian, $A _ { 2 } ( G )$ is precisely the [[Fourier-algebra(2)|Fourier algebra]] of $G$. |
| | | | |
| − | 3) The dual <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f130/f130100/f13010079.png" /> of the Banach space <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f130/f130100/f13010080.png" /> is canonically isometrically isomorphic to <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f130/f130100/f13010081.png" />. Also, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f130/f130100/f13010082.png" /> with the topology <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f130/f130100/f13010083.png" /> is homeomorphic to <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f130/f130100/f13010084.png" /> with the ultraweak operator topology on <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f130/f130100/f13010085.png" />. As a consequence, for <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f130/f130100/f13010086.png" /> amenable or for <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f130/f130100/f13010087.png" /> arbitrary but with <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f130/f130100/f13010088.png" />, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f130/f130100/f13010089.png" />.
| + | 2) If $G$ is amenable, then $A _ { 2 } ( G ) \subset A _ { p } ( G )$. The algebra $A _ { p } ( G )$ is a useful tool for studying the $p$-convolution operators of $G$ (see [[#References|[a2]]], [[#References|[a7]]], [[#References|[a8]]]). For a function $\varphi$ on $G$ and $a , x \in G$ one sets $\square_{a} \varphi ( x ) = \varphi ( a x )$. A continuous [[Linear operator|linear operator]] $T$ on $L _ { \text{C} } ^ { p } ( G )$ is said to be a $p$-convolution operator of $G$ if $T ( \square _ { \alpha } \varphi ) = \square _ { \alpha } ( T ( \varphi ) )$ for every $a \in G$ and every $\varphi \in L _ { \text{C} } ^ { p } ( G )$. Let $C V _ { p } ( G )$ be the set of all $p$-convolution operators of $G$. It is a closed subalgebra of the Banach algebra $\mathcal{L} ( L _ { \text{C} } ^ { p } ( G ) )$ of all continuous linear operators on $L _ { \text{C} } ^ { p } ( G )$. For a complex bounded [[Measure|measure]] $\mu$ on $G$ (i.e. $\mu \in M _ { \text{C} } ^ {1} ( G )$) and a continuous complex-valued function $\varphi$ with compact support on $G$ ($\varphi \in C _ { 00 } ( G ; \mathbf C )$), the rule $\lambda ^ { p } ( \mu ) [ \varphi ] = [ \varphi * \Delta _ { G } ^ { 1 / p ^ { \prime } } \check{\mu} ]$ defines a $p$-convolution operator $\lambda ^ { p } ( \mu )$. Of course, for $f \in \mathbf{C} ^ { G }$, $[ f ]$ denotes the set of all $g \in \mathbf{C} ^ { G }$ with $g ( x ) = f ( x )$ $m$-almost everywhere. |
| | | | |
| − | This duality between <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f130/f130100/f13010090.png" /> and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f130/f130100/f13010091.png" /> also permits one to develop (see [[#References|[a1]]]) a kind of "non-commutative harmonic analysis on G" , where (for <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f130/f130100/f13010092.png" /> Abelian) <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f130/f130100/f13010093.png" /> replaces <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f130/f130100/f13010094.png" /> and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f130/f130100/f13010095.png" /> replaces <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f130/f130100/f13010096.png" />. (Cf. also [[Harmonic analysis, abstract|Harmonic analysis, abstract]].)
| + | Even for $G = \mathbf{R}$ one has $C V _ { p } ( G ) \neq \lambda ^ { p } ( M ^ { 1 } ( G ) )$. Let $P M _ { p } ( G )$ be the closure in $C V _ { p } ( G )$ of $\lambda ^ { p } ( M ^ { 1 } ( G ) )$ with respect to the ultraweak operator topology on $\mathcal{L} ( L _ { \text{C} } ^ { p } ( G ) )$. |
| | | | |
| − | Let <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f130/f130100/f13010097.png" />. Then the support of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f130/f130100/f13010098.png" />, denoted by <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f130/f130100/f13010099.png" />, is the set of all <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f130/f130100/f130100100.png" /> for which for all open subsets <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f130/f130100/f130100101.png" />, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f130/f130100/f130100102.png" />, of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f130/f130100/f130100103.png" /> with <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f130/f130100/f130100104.png" /> and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f130/f130100/f130100105.png" /> there are <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f130/f130100/f130100106.png" /> with <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f130/f130100/f130100107.png" />, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f130/f130100/f130100108.png" /> and
| + | 3) The dual $A _ { p } ( G ) ^ { \prime }$ of the Banach space $A _ { p } ( G )$ is canonically isometrically isomorphic to $P M _ { p } ( G )$. Also, $A _ { p } ( G ) ^ { \prime }$ with the topology $\sigma ( A _ { p } ( G ) ^ { \prime } , A _ { p } ( G ) )$ is homeomorphic to $P M _ { p } ( G )$ with the ultraweak operator topology on $\mathcal{L} ( L _ { \text{C} } ^ { p } ( G ) )$. As a consequence, for $G$ amenable or for $G$ arbitrary but with $p = 2$, $P M _ { p } ( G ) = C V _ { p } ( G )$. |
| | | | |
| − | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f130/f130100/f130100109.png" /></td> </tr></table>
| + | This duality between $A _ { p } ( G )$ and $P M _ { p } ( G )$ also permits one to develop (see [[#References|[a1]]]) a kind of "non-commutative harmonic analysis on G" , where (for $G$ Abelian) $A _ { p } ( G )$ replaces $L _ { \text{C} } ^ { 1 } ( \hat { G } )$ and $C V _ { p } ( G )$ replaces $L _ { C } ^ { \infty } ( \hat { G } )$. (Cf. also [[Harmonic analysis, abstract|Harmonic analysis, abstract]].) |
| | | | |
| − | If <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f130/f130100/f130100110.png" />, then <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f130/f130100/f130100111.png" />. For <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f130/f130100/f130100112.png" /> Abelian, let <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f130/f130100/f130100113.png" /> be the canonical mapping from <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f130/f130100/f130100114.png" /> onto <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f130/f130100/f130100115.png" />. Then <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f130/f130100/f130100116.png" />, where <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f130/f130100/f130100117.png" />, is an isometric isomorphism of the Banach algebra <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f130/f130100/f130100118.png" /> onto <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f130/f130100/f130100119.png" />. Let <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f130/f130100/f130100120.png" /> and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f130/f130100/f130100121.png" />. Then <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f130/f130100/f130100122.png" /> "belongs to the spectrum of u" (written as <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f130/f130100/f130100123.png" />) if <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f130/f130100/f130100124.png" /> lies in the closure of the linear span of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f130/f130100/f130100125.png" /> in <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f130/f130100/f130100126.png" />, for the [[Weak topology|weak topology]] <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f130/f130100/f130100127.png" />. Let <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f130/f130100/f130100128.png" />; then <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f130/f130100/f130100129.png" />. For <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f130/f130100/f130100130.png" /> not necessarily amenable and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f130/f130100/f130100131.png" />, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f130/f130100/f130100132.png" /> if and only <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f130/f130100/f130100133.png" /> is empty. This assertion is a non-commutative version of the Wiener theorem! Similarly, there is also a version of the Carleman–Kaplansky theorem: for <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f130/f130100/f130100134.png" />, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f130/f130100/f130100135.png" /> if and only there exist <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f130/f130100/f130100136.png" /> such that <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f130/f130100/f130100137.png" />, where <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f130/f130100/f130100138.png" /> denotes the Dirac measure in <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f130/f130100/f130100139.png" /> (cf. also [[Dirac distribution|Dirac distribution]]). In fact, even for <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f130/f130100/f130100140.png" /> or for <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f130/f130100/f130100141.png" /> (but <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f130/f130100/f130100142.png" />) the situation is not classical!
| + | Let $T \in C V _ { p } ( G )$. Then the support of $T$, denoted by <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f130/f130100/f13010099.png"/>, is the set of all $x \in G$ for which for all open subsets $U$, $V$, of $G$ with $e \in U$ and $x \in \mathbf{V}$ there are $\phi , \psi \in C _ { 00 } ( G ; \mathbf{C} )$ with $\text{supp}\, \phi \subset U$, $\operatorname{supp} \psi \subset V$ and |
| | | | |
| − | The Banach space <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f130/f130100/f130100143.png" /> has been first introduced by A. Figà-Talamanca in [[#References|[a3]]] for <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f130/f130100/f130100144.png" /> Abelian or <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f130/f130100/f130100145.png" /> non-Abelian but compact. For these classes of groups he obtained assertion 3) above. The statement for a general locally compact group is due to C.S. Herz [[#References|[a5]]]. Assertion 1) is also due to Herz [[#References|[a4]]].
| + | \begin{equation*} \langle T [ \phi ] , [ \psi ] \rangle _ { L _ { \text{C} } ^ { p } ( G ) , L _ { \text{C} } ^ { p^{\prime} } ( G ) } \neq 0. \end{equation*} |
| | | | |
| − | The Banach algebra <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f130/f130100/f130100146.png" /> also satisfies the following properties:
| + | If $\mu \in M _ { \text{C} } ^ {1} ( G )$, then $\operatorname {supp}\lambda _ { G } ^ { p } ( \mu ) = ( \operatorname { supp } \mu ) ^ { - 1 }$. For $G$ Abelian, let $\varepsilon$ be the canonical mapping from $G$ onto $\widehat {\widehat {G} }$. Then $f \mapsto ( \widehat { f } \circ \varepsilon )$, where $ \check{\varphi} ( \chi ) = \varphi ( \chi ^ { - 1 } )$, is an isometric isomorphism of the Banach algebra $L ^ { 1 } ( \hat { G } )$ onto $A _ { 2 } ( G )$. Let $u \in L _ { \text{C} } ^ { \infty } ( \hat { G } )$ and $x \in G$. Then $x$ "belongs to the spectrum of u" (written as $x \in \operatorname { sp } u$) if $[ \epsilon ( x ) ]$ lies in the [[linear closure]] of $\left\{ \square _ { \chi } u : \chi \in \widehat { G } \right\}$ in $L _ { C } ^ { \infty } ( \hat { G } )$, for the [[Weak topology|weak topology]] $\sigma ( L _ {\bf C } ^ { \infty } ( \hat { G } ) , L _ {\bf C } ^ { 1 } ( \hat { G } ) )$. Let $T \in C V _ { p } ( G )$; then $\operatorname {sp} \hat { T } = ( \operatorname { supp } T ) ^ { - 1 }$. For $G$ not necessarily amenable and $T \in C V _ { p } ( G )$, $T = 0$ if and only <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f130/f130100/f130100133.png"/> is empty. This assertion is a non-commutative version of the Wiener theorem! Similarly, there is also a version of the Carleman–Kaplansky theorem: for $T \in C V _ { p } ( G )$, $\operatorname { supp } T = \{ x _ { 1 } , \dots , x _ { n } \}$ if and only there exist $c_1 , \ldots , c_n \in \mathbf{C}$ such that $T = c _ { 1 } \lambda ^ { p } ( \delta _ { x _ { 1 } } ) + \ldots + c _ { n } \lambda ^ { p } ( \delta _ { x _ { n } } )$, where $\delta _ { x }$ denotes the Dirac measure in $x$ (cf. also [[Dirac distribution|Dirac distribution]]). In fact, even for $G = \mathbf{T}$ or for $G = \mathbf{R}$ (but $p \neq 2$) the situation is not classical! |
| | | | |
| − | a) Let <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f130/f130100/f130100147.png" /> be a closed subgroup of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f130/f130100/f130100148.png" />. Then <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f130/f130100/f130100149.png" />. More precisely, for every <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f130/f130100/f130100150.png" /> and for every <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f130/f130100/f130100151.png" /> there is a <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f130/f130100/f130100152.png" /> with <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f130/f130100/f130100153.png" /> and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f130/f130100/f130100154.png" /> (see [[#References|[a5]]]).
| + | The Banach space $A _ { p } ( G )$ has been first introduced by A. Figà-Talamanca in [[#References|[a3]]] for $G$ Abelian or $G$ non-Abelian but compact. For these classes of groups he obtained assertion 3) above. The statement for a general locally compact group is due to C.S. Herz [[#References|[a5]]]. Assertion 1) is also due to Herz [[#References|[a4]]]. |
| | | | |
| − | b) The Banach algebra <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f130/f130100/f130100155.png" /> has bounded approximate units (i.e. there is a <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f130/f130100/f130100156.png" /> such that for every <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f130/f130100/f130100157.png" /> and for every <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f130/f130100/f130100158.png" /> there is a <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f130/f130100/f130100159.png" /> with <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f130/f130100/f130100160.png" /> and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f130/f130100/f130100161.png" />) if and only if the locally compact group <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f130/f130100/f130100162.png" /> is amenable (see [[#References|[a5]]] and [[#References|[a6]]] for <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f130/f130100/f130100163.png" />). This algebra is often called the Figà-Talamanca–Herz algebra.
| + | The Banach algebra $A _ { p }$ also satisfies the following properties: |
| | + | |
| | + | a) Let $H$ be a closed subgroup of $G$. Then $\operatorname { Res } _ { H } A _ { p } ( G ) = A _ { p } ( H )$. More precisely, for every $u \in A _ { p } ( H )$ and for every $\epsilon > 0$ there is a $v \in A _ { p } ( G )$ with $\operatorname { Res } _ { H } v = u$ and $\|v\|_{A_p (G)} \leq \| u \| _ { A_p(H) } + \epsilon$ (see [[#References|[a5]]]). |
| | + | |
| | + | b) The Banach algebra $A _ { p } ( G )$ has bounded approximate units (i.e. there is a $C > 0$ such that for every $u \in A _ { p } ( G )$ and for every $\epsilon > 0$ there is a $v \in A _ { p } ( G )$ with $\|v \| _ { A _ { p } ( G ) } \leq C$ and $\| u - u v \| _ { A _ { p } ( G ) } < \epsilon$) if and only if the locally compact group $G$ is amenable (see [[#References|[a5]]] and [[#References|[a6]]] for $p = 2$). This algebra is often called the Figà-Talamanca–Herz algebra. |
| | | | |
| | See also [[Fourier-algebra(2)|Fourier algebra]]. | | See also [[Fourier-algebra(2)|Fourier algebra]]. |
| | | | |
| | ====References==== | | ====References==== |
| − | <table><TR><TD valign="top">[a1]</TD> <TD valign="top"> A. Derighetti, "Quelques observations concernant les ensembles de Ditkin d'un groupe localement compact" ''Monatsh. Math.'' , '''101''' (1986) pp. 95–113</TD></TR><TR><TD valign="top">[a2]</TD> <TD valign="top"> P. Eymard, "Algèbres <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f130/f130100/f130100164.png" /> et convoluteurs de <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f130/f130100/f130100165.png" />" , ''Sem. Bourbaki 1969/70, Exp. 367'' , ''Lecture Notes in Math.'' , '''180''' , Springer (1971) pp. 364–381</TD></TR><TR><TD valign="top">[a3]</TD> <TD valign="top"> A. Figà-Talamanca, "Translation invariant operators in <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f130/f130100/f130100166.png" />" ''Duke Math. J.'' , '''32''' (1965) pp. 495–501</TD></TR><TR><TD valign="top">[a4]</TD> <TD valign="top"> C. Herz, "The theory of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f130/f130100/f130100167.png" />-spaces" ''Trans. Amer. Math. Soc.'' , '''154''' (1971) pp. 69–82</TD></TR><TR><TD valign="top">[a5]</TD> <TD valign="top"> C. Herz, "Harmonic synthesis for subgroups" ''Ann. Inst. Fourier (Grenoble)'' , '''23''' : 3 (1973) pp. 91–123</TD></TR><TR><TD valign="top">[a6]</TD> <TD valign="top"> H. Leptin, "Sur l'algèbre de Fourier d'un groupe localement compact" ''C.R. Acad. Sci. Paris Sér. A'' , '''266''' (1968) pp. 1180–1182</TD></TR><TR><TD valign="top">[a7]</TD> <TD valign="top"> N. Lohoué, "Algèbres <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f130/f130100/f130100168.png" /> et convoluteurs de <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f130/f130100/f130100169.png" />" ''Thèse, Univ. Paris-Sud'' (1971)</TD></TR><TR><TD valign="top">[a8]</TD> <TD valign="top"> N. Lohoué, "Estimations <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f130/f130100/f130100170.png" /> des coefficients de représentations et opérateurs de convolution" ''Adv. Math.'' , '''38''' (1980) pp. 178–221</TD></TR><TR><TD valign="top">[a9]</TD> <TD valign="top"> J.R. McMullen, "Extensions of positive-definite functions" ''Memoirs Amer. Math. Soc.'' , '''117''' (1972)</TD></TR><TR><TD valign="top">[a10]</TD> <TD valign="top"> J.-P. Pier, "Amenable locally compact groups" , Wiley (1984)</TD></TR></table> | + | <table><tr><td valign="top">[a1]</td> <td valign="top"> A. Derighetti, "Quelques observations concernant les ensembles de Ditkin d'un groupe localement compact" ''Monatsh. Math.'' , '''101''' (1986) pp. 95–113</td></tr><tr><td valign="top">[a2]</td> <td valign="top"> P. Eymard, "Algèbres $A _ { p }$ et convoluteurs de $L ^ { p } ( G )$" , ''Sem. Bourbaki 1969/70, Exp. 367'' , ''Lecture Notes in Math.'' , '''180''' , Springer (1971) pp. 364–381</td></tr><tr><td valign="top">[a3]</td> <td valign="top"> A. Figà-Talamanca, "Translation invariant operators in $L ^ { p }$" ''Duke Math. J.'' , '''32''' (1965) pp. 495–501</td></tr><tr><td valign="top">[a4]</td> <td valign="top"> C. Herz, "The theory of $p$-spaces" ''Trans. Amer. Math. Soc.'' , '''154''' (1971) pp. 69–82</td></tr><tr><td valign="top">[a5]</td> <td valign="top"> C. Herz, "Harmonic synthesis for subgroups" ''Ann. Inst. Fourier (Grenoble)'' , '''23''' : 3 (1973) pp. 91–123</td></tr><tr><td valign="top">[a6]</td> <td valign="top"> H. Leptin, "Sur l'algèbre de Fourier d'un groupe localement compact" ''C.R. Acad. Sci. Paris Sér. A'' , '''266''' (1968) pp. 1180–1182</td></tr><tr><td valign="top">[a7]</td> <td valign="top"> N. Lohoué, "Algèbres $A _ { p }$ et convoluteurs de $L ^ { p } ( G )$" ''Thèse, Univ. Paris-Sud'' (1971)</td></tr><tr><td valign="top">[a8]</td> <td valign="top"> N. Lohoué, "Estimations $L ^ { p }$ des coefficients de représentations et opérateurs de convolution" ''Adv. Math.'' , '''38''' (1980) pp. 178–221</td></tr><tr><td valign="top">[a9]</td> <td valign="top"> J.R. McMullen, "Extensions of positive-definite functions" ''Memoirs Amer. Math. Soc.'' , '''117''' (1972)</td></tr><tr><td valign="top">[a10]</td> <td valign="top"> J.-P. Pier, "Amenable locally compact groups" , Wiley (1984)</td></tr></table> |
Let $G$ be a locally compact group, $1 < p < \infty$ and $p ^ { \prime } = p / p - 1$. Consider the set $\mathcal{A} _ { p } ( G )$ of all pairs $( ( k _ { n } ) _ { n = 1 } ^ { \infty } , ( l _ { n } ) _ { n = 1 } ^ { \infty } )$, with $( k _ { n } ) _ { n = 1 } ^ { \infty }$ a sequence in ${\cal L} _ {\bf C } ^ { p } ( G )$ and $( l _ { n } ) _ { n = 1 } ^ { \infty } $ a sequence in $\mathcal{L} _ { \text{C} } ^ { p ^ { \prime } } ( G )$ such that $\sum _ { n = 1 } ^ { \infty } N _ { p } ( k _ { n } ) N _ { p^{\prime} } ( l _ { n } ) < \infty$. Here, $N _ { p } ( f )$ is defined by $N _ { p } ( f ) = ( \int _ { G } | f ( x ) | ^ { p } d m ( x ) ) ^ { 1 / p }$, where $m$ is some left-invariant Haar measure on $G$. Let $A _ { p } ( G )$ denote the set of all $u \in {\bf C} ^ { G }$ for which there is a pair $( ( k _ { n } ) _ { n = 1 } ^ { \infty } , ( l _ { n } ) _ { n = 1 } ^ { \infty } ) \in \mathcal{A} _ { p } ( G )$ such that $u ( x ) = \sum _ { n = 1 } ^ { \infty } \overline { k _ { n } } * \check{l} _ { n } ( x )$, where $\check{\varphi} { P } ( x ) = \varphi ( x ^ { - 1 } )$. The set $A _ { p } ( G )$ is a linear subspace of the $\mathbf{C}$-vector space of all continuous complex-valued functions on $G$ vanishing at infinity. For $u \in A _ { p } ( G )$ one sets
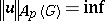 |
\begin{equation*} \left\{ \sum _ { n = 1 } ^ { \infty } N _ { p } ( k _ { n } ) N _ { p^{\prime} } ( l _ { n } ) : \begin{array} { c c } {((k_n)^{\infty}_{n=1} , (l_n)^{\infty}_{n=1}) \in \mathcal{A}_{p} (G) } \\ {\text { with } u = \sum _ { n = 1 } ^ { \infty } \overline { k _ { n } } * \check{l}_ { n }} \end{array} \right\}. \end{equation*}
1) For the pointwise product on $G$, $A _ { p } ( G )$ is a Banach algebra. This algebra is called the Figà-Talamanca algebra of $G$. If $G$ is Abelian, $A _ { 2 } ( G )$ is isometrically isomorphic to $L _ { \text{C} } ^ { 1 } ( \hat { G } )$, where $\hat { C }$ is the dual group of $G$. For $G$ not necessarily Abelian, $A _ { 2 } ( G )$ is precisely the Fourier algebra of $G$.
2) If $G$ is amenable, then $A _ { 2 } ( G ) \subset A _ { p } ( G )$. The algebra $A _ { p } ( G )$ is a useful tool for studying the $p$-convolution operators of $G$ (see [a2], [a7], [a8]). For a function $\varphi$ on $G$ and $a , x \in G$ one sets $\square_{a} \varphi ( x ) = \varphi ( a x )$. A continuous linear operator $T$ on $L _ { \text{C} } ^ { p } ( G )$ is said to be a $p$-convolution operator of $G$ if $T ( \square _ { \alpha } \varphi ) = \square _ { \alpha } ( T ( \varphi ) )$ for every $a \in G$ and every $\varphi \in L _ { \text{C} } ^ { p } ( G )$. Let $C V _ { p } ( G )$ be the set of all $p$-convolution operators of $G$. It is a closed subalgebra of the Banach algebra $\mathcal{L} ( L _ { \text{C} } ^ { p } ( G ) )$ of all continuous linear operators on $L _ { \text{C} } ^ { p } ( G )$. For a complex bounded measure $\mu$ on $G$ (i.e. $\mu \in M _ { \text{C} } ^ {1} ( G )$) and a continuous complex-valued function $\varphi$ with compact support on $G$ ($\varphi \in C _ { 00 } ( G ; \mathbf C )$), the rule $\lambda ^ { p } ( \mu ) [ \varphi ] = [ \varphi * \Delta _ { G } ^ { 1 / p ^ { \prime } } \check{\mu} ]$ defines a $p$-convolution operator $\lambda ^ { p } ( \mu )$. Of course, for $f \in \mathbf{C} ^ { G }$, $[ f ]$ denotes the set of all $g \in \mathbf{C} ^ { G }$ with $g ( x ) = f ( x )$ $m$-almost everywhere.
Even for $G = \mathbf{R}$ one has $C V _ { p } ( G ) \neq \lambda ^ { p } ( M ^ { 1 } ( G ) )$. Let $P M _ { p } ( G )$ be the closure in $C V _ { p } ( G )$ of $\lambda ^ { p } ( M ^ { 1 } ( G ) )$ with respect to the ultraweak operator topology on $\mathcal{L} ( L _ { \text{C} } ^ { p } ( G ) )$.
3) The dual $A _ { p } ( G ) ^ { \prime }$ of the Banach space $A _ { p } ( G )$ is canonically isometrically isomorphic to $P M _ { p } ( G )$. Also, $A _ { p } ( G ) ^ { \prime }$ with the topology $\sigma ( A _ { p } ( G ) ^ { \prime } , A _ { p } ( G ) )$ is homeomorphic to $P M _ { p } ( G )$ with the ultraweak operator topology on $\mathcal{L} ( L _ { \text{C} } ^ { p } ( G ) )$. As a consequence, for $G$ amenable or for $G$ arbitrary but with $p = 2$, $P M _ { p } ( G ) = C V _ { p } ( G )$.
This duality between $A _ { p } ( G )$ and $P M _ { p } ( G )$ also permits one to develop (see [a1]) a kind of "non-commutative harmonic analysis on G" , where (for $G$ Abelian) $A _ { p } ( G )$ replaces $L _ { \text{C} } ^ { 1 } ( \hat { G } )$ and $C V _ { p } ( G )$ replaces $L _ { C } ^ { \infty } ( \hat { G } )$. (Cf. also Harmonic analysis, abstract.)
Let $T \in C V _ { p } ( G )$. Then the support of $T$, denoted by 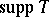 , is the set of all $x \in G$ for which for all open subsets $U$, $V$, of $G$ with $e \in U$ and $x \in \mathbf{V}$ there are $\phi , \psi \in C _ { 00 } ( G ; \mathbf{C} )$ with $\text{supp}\, \phi \subset U$, $\operatorname{supp} \psi \subset V$ and
, is the set of all $x \in G$ for which for all open subsets $U$, $V$, of $G$ with $e \in U$ and $x \in \mathbf{V}$ there are $\phi , \psi \in C _ { 00 } ( G ; \mathbf{C} )$ with $\text{supp}\, \phi \subset U$, $\operatorname{supp} \psi \subset V$ and
\begin{equation*} \langle T [ \phi ] , [ \psi ] \rangle _ { L _ { \text{C} } ^ { p } ( G ) , L _ { \text{C} } ^ { p^{\prime} } ( G ) } \neq 0. \end{equation*}
If $\mu \in M _ { \text{C} } ^ {1} ( G )$, then $\operatorname {supp}\lambda _ { G } ^ { p } ( \mu ) = ( \operatorname { supp } \mu ) ^ { - 1 }$. For $G$ Abelian, let $\varepsilon$ be the canonical mapping from $G$ onto $\widehat {\widehat {G} }$. Then $f \mapsto ( \widehat { f } \circ \varepsilon )$, where $ \check{\varphi} ( \chi ) = \varphi ( \chi ^ { - 1 } )$, is an isometric isomorphism of the Banach algebra $L ^ { 1 } ( \hat { G } )$ onto $A _ { 2 } ( G )$. Let $u \in L _ { \text{C} } ^ { \infty } ( \hat { G } )$ and $x \in G$. Then $x$ "belongs to the spectrum of u" (written as $x \in \operatorname { sp } u$) if $[ \epsilon ( x ) ]$ lies in the linear closure of $\left\{ \square _ { \chi } u : \chi \in \widehat { G } \right\}$ in $L _ { C } ^ { \infty } ( \hat { G } )$, for the weak topology $\sigma ( L _ {\bf C } ^ { \infty } ( \hat { G } ) , L _ {\bf C } ^ { 1 } ( \hat { G } ) )$. Let $T \in C V _ { p } ( G )$; then $\operatorname {sp} \hat { T } = ( \operatorname { supp } T ) ^ { - 1 }$. For $G$ not necessarily amenable and $T \in C V _ { p } ( G )$, $T = 0$ if and only 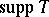 is empty. This assertion is a non-commutative version of the Wiener theorem! Similarly, there is also a version of the Carleman–Kaplansky theorem: for $T \in C V _ { p } ( G )$, $\operatorname { supp } T = \{ x _ { 1 } , \dots , x _ { n } \}$ if and only there exist $c_1 , \ldots , c_n \in \mathbf{C}$ such that $T = c _ { 1 } \lambda ^ { p } ( \delta _ { x _ { 1 } } ) + \ldots + c _ { n } \lambda ^ { p } ( \delta _ { x _ { n } } )$, where $\delta _ { x }$ denotes the Dirac measure in $x$ (cf. also Dirac distribution). In fact, even for $G = \mathbf{T}$ or for $G = \mathbf{R}$ (but $p \neq 2$) the situation is not classical!
is empty. This assertion is a non-commutative version of the Wiener theorem! Similarly, there is also a version of the Carleman–Kaplansky theorem: for $T \in C V _ { p } ( G )$, $\operatorname { supp } T = \{ x _ { 1 } , \dots , x _ { n } \}$ if and only there exist $c_1 , \ldots , c_n \in \mathbf{C}$ such that $T = c _ { 1 } \lambda ^ { p } ( \delta _ { x _ { 1 } } ) + \ldots + c _ { n } \lambda ^ { p } ( \delta _ { x _ { n } } )$, where $\delta _ { x }$ denotes the Dirac measure in $x$ (cf. also Dirac distribution). In fact, even for $G = \mathbf{T}$ or for $G = \mathbf{R}$ (but $p \neq 2$) the situation is not classical!
The Banach space $A _ { p } ( G )$ has been first introduced by A. Figà-Talamanca in [a3] for $G$ Abelian or $G$ non-Abelian but compact. For these classes of groups he obtained assertion 3) above. The statement for a general locally compact group is due to C.S. Herz [a5]. Assertion 1) is also due to Herz [a4].
The Banach algebra $A _ { p }$ also satisfies the following properties:
a) Let $H$ be a closed subgroup of $G$. Then $\operatorname { Res } _ { H } A _ { p } ( G ) = A _ { p } ( H )$. More precisely, for every $u \in A _ { p } ( H )$ and for every $\epsilon > 0$ there is a $v \in A _ { p } ( G )$ with $\operatorname { Res } _ { H } v = u$ and $\|v\|_{A_p (G)} \leq \| u \| _ { A_p(H) } + \epsilon$ (see [a5]).
b) The Banach algebra $A _ { p } ( G )$ has bounded approximate units (i.e. there is a $C > 0$ such that for every $u \in A _ { p } ( G )$ and for every $\epsilon > 0$ there is a $v \in A _ { p } ( G )$ with $\|v \| _ { A _ { p } ( G ) } \leq C$ and $\| u - u v \| _ { A _ { p } ( G ) } < \epsilon$) if and only if the locally compact group $G$ is amenable (see [a5] and [a6] for $p = 2$). This algebra is often called the Figà-Talamanca–Herz algebra.
See also Fourier algebra.
References
| [a1] | A. Derighetti, "Quelques observations concernant les ensembles de Ditkin d'un groupe localement compact" Monatsh. Math. , 101 (1986) pp. 95–113 |
| [a2] | P. Eymard, "Algèbres $A _ { p }$ et convoluteurs de $L ^ { p } ( G )$" , Sem. Bourbaki 1969/70, Exp. 367 , Lecture Notes in Math. , 180 , Springer (1971) pp. 364–381 |
| [a3] | A. Figà-Talamanca, "Translation invariant operators in $L ^ { p }$" Duke Math. J. , 32 (1965) pp. 495–501 |
| [a4] | C. Herz, "The theory of $p$-spaces" Trans. Amer. Math. Soc. , 154 (1971) pp. 69–82 |
| [a5] | C. Herz, "Harmonic synthesis for subgroups" Ann. Inst. Fourier (Grenoble) , 23 : 3 (1973) pp. 91–123 |
| [a6] | H. Leptin, "Sur l'algèbre de Fourier d'un groupe localement compact" C.R. Acad. Sci. Paris Sér. A , 266 (1968) pp. 1180–1182 |
| [a7] | N. Lohoué, "Algèbres $A _ { p }$ et convoluteurs de $L ^ { p } ( G )$" Thèse, Univ. Paris-Sud (1971) |
| [a8] | N. Lohoué, "Estimations $L ^ { p }$ des coefficients de représentations et opérateurs de convolution" Adv. Math. , 38 (1980) pp. 178–221 |
| [a9] | J.R. McMullen, "Extensions of positive-definite functions" Memoirs Amer. Math. Soc. , 117 (1972) |
| [a10] | J.-P. Pier, "Amenable locally compact groups" , Wiley (1984) |
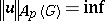
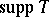 , is the set of all $x \in G$ for which for all open subsets $U$, $V$, of $G$ with $e \in U$ and $x \in \mathbf{V}$ there are $\phi , \psi \in C _ { 00 } ( G ; \mathbf{C} )$ with $\text{supp}\, \phi \subset U$, $\operatorname{supp} \psi \subset V$ and
, is the set of all $x \in G$ for which for all open subsets $U$, $V$, of $G$ with $e \in U$ and $x \in \mathbf{V}$ there are $\phi , \psi \in C _ { 00 } ( G ; \mathbf{C} )$ with $\text{supp}\, \phi \subset U$, $\operatorname{supp} \psi \subset V$ and
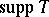 is empty. This assertion is a non-commutative version of the Wiener theorem! Similarly, there is also a version of the Carleman–Kaplansky theorem: for $T \in C V _ { p } ( G )$, $\operatorname { supp } T = \{ x _ { 1 } , \dots , x _ { n } \}$ if and only there exist $c_1 , \ldots , c_n \in \mathbf{C}$ such that $T = c _ { 1 } \lambda ^ { p } ( \delta _ { x _ { 1 } } ) + \ldots + c _ { n } \lambda ^ { p } ( \delta _ { x _ { n } } )$, where $\delta _ { x }$ denotes the Dirac measure in $x$ (cf. also Dirac distribution). In fact, even for $G = \mathbf{T}$ or for $G = \mathbf{R}$ (but $p \neq 2$) the situation is not classical!
is empty. This assertion is a non-commutative version of the Wiener theorem! Similarly, there is also a version of the Carleman–Kaplansky theorem: for $T \in C V _ { p } ( G )$, $\operatorname { supp } T = \{ x _ { 1 } , \dots , x _ { n } \}$ if and only there exist $c_1 , \ldots , c_n \in \mathbf{C}$ such that $T = c _ { 1 } \lambda ^ { p } ( \delta _ { x _ { 1 } } ) + \ldots + c _ { n } \lambda ^ { p } ( \delta _ { x _ { n } } )$, where $\delta _ { x }$ denotes the Dirac measure in $x$ (cf. also Dirac distribution). In fact, even for $G = \mathbf{T}$ or for $G = \mathbf{R}$ (but $p \neq 2$) the situation is not classical!