Harmonic analysis, abstract
The theory of abstract Fourier series and Fourier integrals (cf. Fourier integral). Classical harmonic analysis — the theory of Fourier series and Fourier integrals — underwent a rapid development, stimulated by physical problems, in the 18th century and 19th century; P. Dirichlet, B. Riemann, H. Lebesgue, M. Plancherel, L. Fejér, and F. Riesz formulated harmonic analysis as an independent mathematical discipline.
The further development of harmonic analysis resulted in the establishment of various relations between harmonic analysis and general problems in the theory of functions and functional analysis. The discovery of the Haar measure and the development of the theory of representations of infinite groups (cf. Representation of an infinite group), beginning with the work of H. Weyl and F. Peter [1] on the theory of representations of compact groups (cf. Representation of a compact group) and of L.S. Pontryagin [2] on the theory of characters of locally compact Abelian groups (cf. Character of a group), posed the problem of the natural limits of the main results of classical harmonic analysis. This problem is based on the following interpretation of an ordinary Fourier series in complex form. Let 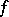 be a complex-valued square-summable function on a circle of unit length (or on the segment
be a complex-valued square-summable function on a circle of unit length (or on the segment 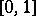 ), and let
), and let 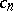 be its Fourier coefficients with respect to the system
be its Fourier coefficients with respect to the system 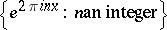 :
:
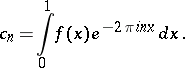 |
Then the Fourier series
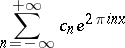 |
of  converges in the mean to
converges in the mean to  in
in 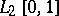 . The Lebesgue measure on
. The Lebesgue measure on 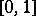 generates the Haar measure on the circle
generates the Haar measure on the circle 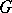 (of length one), regarded as the group of rotations of the plane, while the functions
(of length one), regarded as the group of rotations of the plane, while the functions 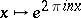 represent a complete collection of irreducible unitary representations (cf. Unitary representation) of the topological group
represent a complete collection of irreducible unitary representations (cf. Unitary representation) of the topological group 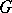 . For this reason all data involved in the definition of a Fourier series acquire a group-theoretic meaning, and it becomes possible to generalize the concept of a Fourier series on the basis of the theory of irreducible unitary representations of topological groups. Here, abstract harmonic analysis not only makes it possible to find a natural form for results of classical harmonic analysis on the real line or the circle, but also establishes new results regarding larger classes of topological groups.
. For this reason all data involved in the definition of a Fourier series acquire a group-theoretic meaning, and it becomes possible to generalize the concept of a Fourier series on the basis of the theory of irreducible unitary representations of topological groups. Here, abstract harmonic analysis not only makes it possible to find a natural form for results of classical harmonic analysis on the real line or the circle, but also establishes new results regarding larger classes of topological groups.
Abstract harmonic analysis as the harmonic analysis on groups was developed mainly on the basis of the theory of characters of locally compact Abelian groups established by Pontryagin ([2], see also [7], [8], [9]). Abstract harmonic analysis is one of the natural fields of application of methods of the theory of Banach algebras, and may be regarded as being, to some extent, a branch of this theory. On the other hand, the framework of abstract harmonic analysis is a natural one for a number of classical problems in the theory of functions and functional analysis.
The applications of abstract harmonic analysis are extremely varied. The results are used in the general theory of locally compact groups (e.g. in structure theorems), in the theory of dynamical systems, in the theory of representations of infinite groups (which in its turn is one of the principal tools of abstract harmonic analysis), and in many other mathematical theories.
The best developed branch of abstract harmonic analysis is the theory of Fourier integrals on a locally compact Abelian group. A special type of non-commutative groups are the compact groups, the theory of representations of which is especially simple and complete: solutions of many classical problems of harmonic analysis have been obtained for compact groups. In the case of non-compact non-commutative groups the general theory is still far from complete (1989). However, even in this case one knows the natural limits of a number of fundamental results of classical harmonic analysis.
The connection between the problems of abstract harmonic analysis and the theory of Banach algebras is based on the fact that it is possible to construct two Banach algebras on each locally compact topological group 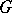 , which both play a major role in the theory of representations of
, which both play a major role in the theory of representations of 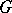 : the group algebra (cf. Group algebra of a locally compact group) and the measure algebra
: the group algebra (cf. Group algebra of a locally compact group) and the measure algebra 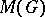 (cf. Algebra of measures), which is defined as follows. Let
(cf. Algebra of measures), which is defined as follows. Let 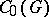 be the set of continuous functions
be the set of continuous functions 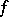 on
on 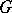 which vanish at infinity, and let
which vanish at infinity, and let 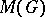 be its dual space, the Banach space of bounded regular measures (cf. Regular measure) on
be its dual space, the Banach space of bounded regular measures (cf. Regular measure) on 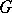 . If a multiplication — the convolution
. If a multiplication — the convolution 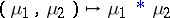 — and an involution
— and an involution 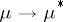 are introduced on
are introduced on 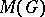 by means of the relations
by means of the relations
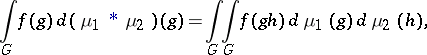 |
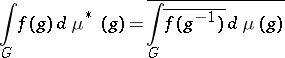 |
for all  , then
, then 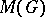 is converted into a Banach algebra with involution, which is called the measure algebra of the group
is converted into a Banach algebra with involution, which is called the measure algebra of the group 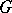 . If
. If 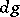 is the left-invariant Haar measure on
is the left-invariant Haar measure on 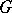 , the association to each element
, the association to each element 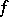 of the group algebra
of the group algebra 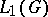 of the measure
of the measure 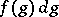 yields an isometric mapping of
yields an isometric mapping of 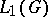 into a closed subalgebra of
into a closed subalgebra of  which preserves the involution. In this sense
which preserves the involution. In this sense 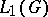 may be considered as a closed subalgebra of
may be considered as a closed subalgebra of 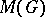 .
.
Abstract harmonic analysis on a locally compact Abelian group.
The following facts are required to construct a Fourier integral on a locally compact Abelian group 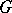 . Any irreducible unitary representation of
. Any irreducible unitary representation of 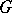 is one-dimensional and defines a continuous homomorphism from
is one-dimensional and defines a continuous homomorphism from 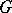 into the multiplicative group
into the multiplicative group 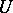 of complex numbers of modulus 1. Such a mapping
of complex numbers of modulus 1. Such a mapping 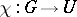 is called a unitary character of
is called a unitary character of 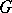 . Let
. Let 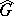 be the group of continuous characters of
be the group of continuous characters of 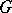 . Pontryagin's duality theorem states that the mapping
. Pontryagin's duality theorem states that the mapping
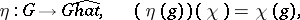 |
where 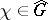 ,
, 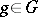 , is a topological isomorphism of
, is a topological isomorphism of  onto
onto 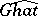 [2], [3], [4], [6]. The group
[2], [3], [4], [6]. The group 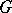 is compact if and only if the group
is compact if and only if the group 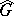 dual to it is discrete. The group of characters of the additive group
dual to it is discrete. The group of characters of the additive group 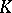 of a non-discrete locally compact field is isomorphic to
of a non-discrete locally compact field is isomorphic to 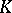 ; the group of characters of the group
; the group of characters of the group 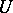 is isomorphic to the group
is isomorphic to the group 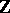 of integers. If
of integers. If 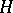 is a closed subgroup of
is a closed subgroup of 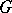 and
and 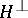 is the set of
is the set of 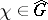 such that
such that  on
on 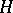 , then
, then 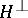 is a closed subgroup of
is a closed subgroup of 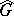 ,
,  ,
, 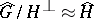 , and any unitary character of the subgroup
, and any unitary character of the subgroup 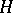 can be extended to a unitary character of the group
can be extended to a unitary character of the group 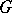 .
.
The Fourier integral on the group 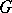 (or the Fourier transform on the group
(or the Fourier transform on the group 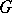 ) is the mapping
) is the mapping 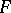 under which a measure
under which a measure  corresponds to the function
corresponds to the function 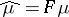 on
on 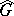 defined by the equation
defined by the equation
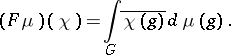 |
The Fourier cotransform is the mapping 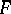 defined by the equation
defined by the equation
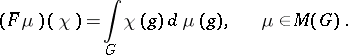 |
For 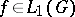 the function
the function 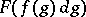 is denoted by
is denoted by 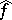 or
or 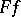 (or, correspondingly,
(or, correspondingly, 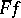 ). The mappings
). The mappings  and
and 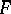 are monomorphisms (cf. Monomorphism) of
are monomorphisms (cf. Monomorphism) of 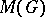 into
into 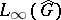 ; the image of
; the image of 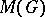 under these mappings is the algebra
under these mappings is the algebra 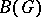 of linear combinations of continuous positive-definite functions on
of linear combinations of continuous positive-definite functions on 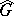 . The generalized Bochner theorem applies [4], [6]: The function
. The generalized Bochner theorem applies [4], [6]: The function 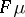 is a positive-definite function on
is a positive-definite function on 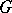 if and only if
if and only if 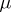 is a positive measure, and then
is a positive measure, and then
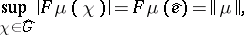 |
where 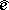 is the unit of
is the unit of  .
.
The topological space  is canonically homeomorphic to the spectrum of the ring
is canonically homeomorphic to the spectrum of the ring 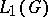 (i.e. to the space of maximal ideals of the algebra
(i.e. to the space of maximal ideals of the algebra 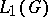 ). In fact, with a character
). In fact, with a character 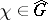 is associated the corresponding character of the commutative algebra
is associated the corresponding character of the commutative algebra  defined by the formula
defined by the formula
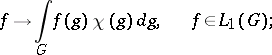 |
the Fourier cotransform 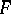 is identical on
is identical on 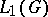 with the Gel'fand representation of the Banach algebra
with the Gel'fand representation of the Banach algebra 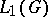 . The spectrum of
. The spectrum of 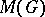 is usually not homeomorphic to
is usually not homeomorphic to 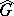 .
.
Let 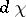 be the Haar measure on
be the Haar measure on 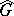 and let
and let 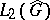 be the corresponding Hilbert space. The following Plancherel theorem [4], [16] is valid: If
be the corresponding Hilbert space. The following Plancherel theorem [4], [16] is valid: If 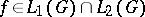 , then
, then 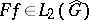 and, if the measures
and, if the measures 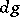 and
and 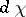 are normalized in a certain way, then the mapping
are normalized in a certain way, then the mapping 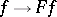 from the set
from the set 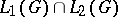 into
into 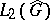 can be uniquely extended to a unitary operator
can be uniquely extended to a unitary operator 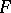 from
from 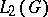 onto
onto 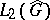 . This operator is known as the Fourier transform on
. This operator is known as the Fourier transform on 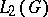 . In such a case the measures
. In such a case the measures 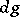 and
and 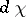 are called compatible. Let
are called compatible. Let 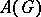 denote the linear subspace of
denote the linear subspace of 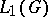 generated by the functions of the form
generated by the functions of the form  where
where 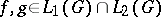 . The following Fourier inversion formula [4], [16] holds: If
. The following Fourier inversion formula [4], [16] holds: If 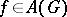 , then
, then 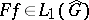 , and for all
, and for all 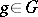 the equation
the equation
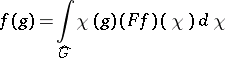 |
is valid, i.e. if 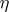 is the canonical mapping of
is the canonical mapping of 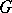 into
into 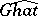 , then
, then 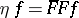 for all
for all 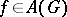 . Let
. Let 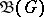 be the set of
be the set of 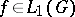 such that
such that 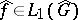 . Then the restriction of
. Then the restriction of 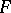 to
to 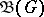 is a one-to-one mapping of
is a one-to-one mapping of 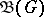 onto
onto 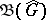 ; the inverse mapping is the restriction of
; the inverse mapping is the restriction of 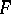 to
to 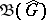 . If
. If 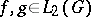 , then
, then 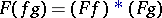 .
.
The classical Poisson summation formula is naturally interpreted in abstract harmonic analysis as follows. Let 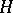 be a closed subgroup of the group
be a closed subgroup of the group 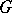 . Let
. Let 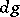 ,
, 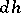 ,
, 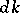 be the Haar measures on
be the Haar measures on 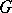 ,
, 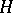 and
and 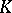 , respectively, normalized so that
, respectively, normalized so that 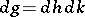 . Let
. Let 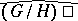 be identified with
be identified with 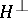 and let
and let 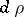 be the Haar measure on
be the Haar measure on 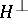 compatible with
compatible with 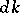 . Finally, let
. Finally, let 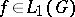 and let the restriction of the continuous function
and let the restriction of the continuous function 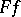 to
to 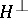 be integrable with respect to
be integrable with respect to 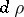 . Then the function
. Then the function 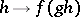 on
on 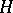 will be integrable with respect to the measure
will be integrable with respect to the measure 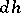 for almost-all
for almost-all 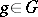 , and
, and
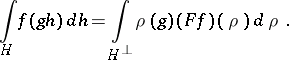 |
This formula is known as the generalized Poisson summation formula.
An important intrinsic problem in abstract harmonic analysis is the study of the Banach algebras 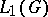 and
and 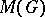 from the point of view of the Fourier transform on
from the point of view of the Fourier transform on 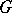 . The algebra
. The algebra 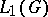 is completely symmetric. The equality
is completely symmetric. The equality 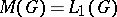 is valid if and only if
is valid if and only if 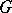 is discrete. If
is discrete. If 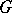 is not discrete,
is not discrete, 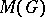 contains non-symmetric maximal ideals. Let
contains non-symmetric maximal ideals. Let 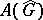 (respectively,
(respectively, 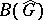 ) be the set of Fourier transforms of elements of
) be the set of Fourier transforms of elements of 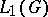 (respectively,
(respectively, 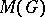 ).
). 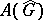 and
and 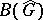 are function algebras on
are function algebras on 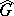 ; moreover,
; moreover, 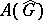 is a regular algebra, and
is a regular algebra, and 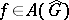 if and only if
if and only if 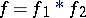 for certain
for certain 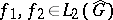 . The set of
. The set of 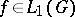 for which the support of the function
for which the support of the function 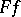 is compact is a dense subset in
is compact is a dense subset in 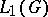 .
.
The following results describe the functional properties of the Fourier transform on 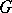 . Let
. Let 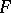 be a function defined on
be a function defined on 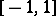 , and let
, and let 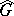 be non-discrete. Let
be non-discrete. Let 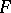 act on
act on 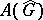 , i.e.
, i.e. 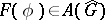 for any function
for any function 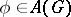 with range in
with range in 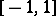 .
. 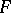 will then be analytic on
will then be analytic on 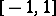 , and if
, and if 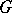 is non-discrete,
is non-discrete,  . Conversely, an analytic function
. Conversely, an analytic function 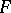 on
on  (
(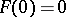 if
if 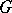 is non-discrete) acts on
is non-discrete) acts on 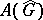 . The function
. The function 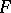 acts on
acts on 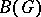 if and only if
if and only if 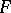 is the restriction to
is the restriction to 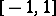 of an entire real-analytic function. Let
of an entire real-analytic function. Let 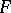 be defined on
be defined on 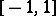 and let
and let 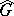 be an infinite discrete group.
be an infinite discrete group. 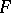 will act on
will act on  if and only if
if and only if 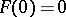 and if
and if 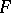 is analytic in a certain neighbourhood of the origin (see [12], [13] for a detailed list of references).
is analytic in a certain neighbourhood of the origin (see [12], [13] for a detailed list of references).
A traditional problem in the theory of Banach algebras is the structure and the properties of closed subalgebras. The following results concern closed subalgebras of the algebra 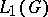 . Let
. Let 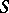 be a Borel semi-group in a locally compact Abelian group
be a Borel semi-group in a locally compact Abelian group 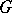 and let
and let 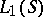 be the maximal subalgebra in
be the maximal subalgebra in  .
. 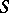 will then be contained in a closed semi-group
will then be contained in a closed semi-group 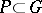 inducing an Archimedean order on
inducing an Archimedean order on 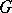 . A commutative Banach algebra
. A commutative Banach algebra 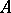 is called a Stone–Weierstrass algebra if any one of its symmetric subalgebras
is called a Stone–Weierstrass algebra if any one of its symmetric subalgebras 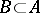 separating the points of the spectrum
separating the points of the spectrum 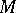 of the ring
of the ring 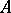 and not vanishing simultaneously at any point of
and not vanishing simultaneously at any point of 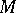 is dense in
is dense in 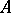 .
. 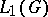 is a Stone–Weierstrass algebra if and only if
is a Stone–Weierstrass algebra if and only if  is totally disconnected.
is totally disconnected.
One field of modern research in abstract harmonic analysis is the theory of thin sets (cf. Thin set) in locally compact Abelian groups, which may be regarded as a generalization of special results of classical harmonic analysis (in particular, the theory of lacunary trigonometric series). Let 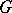 be a locally compact Abelian group and let
be a locally compact Abelian group and let  be its unit element. A set
be its unit element. A set  is called independent if, for any
is called independent if, for any 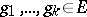 and integers
and integers  , either
, either 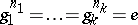 or
or 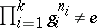 . Any non-discrete locally compact Abelian group contains an independent set homeomorphic to a Cantor set. The independent sets include two important classes of sets, viz. Kronecker sets and
. Any non-discrete locally compact Abelian group contains an independent set homeomorphic to a Cantor set. The independent sets include two important classes of sets, viz. Kronecker sets and 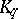 -sets in a
-sets in a 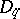 group. A set
group. A set 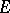 in a locally compact Abelian group is called a Kronecker set if for any continuous function
in a locally compact Abelian group is called a Kronecker set if for any continuous function 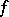 on
on 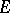 of modulus 1 and for any
of modulus 1 and for any 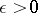 there exists a character
there exists a character 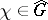 such that
such that
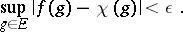 |
A Kronecker set is independent and contains no elements of finite order. Let 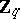 be the cyclic group of order
be the cyclic group of order 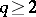 and let
and let  be the direct product of a countably-infinite number of groups isomorphic to
be the direct product of a countably-infinite number of groups isomorphic to 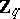 . A set
. A set 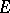 in
in 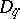 is called a
is called a 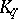 -set if any continuous function
-set if any continuous function  (
(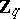 is considered to be a group of roots of unity) coincides on
is considered to be a group of roots of unity) coincides on 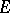 with some unitary character of the group
with some unitary character of the group 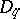 .
. 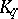 -sets are independent. If in each neighbourhood of the unit element of a locally compact group
-sets are independent. If in each neighbourhood of the unit element of a locally compact group 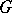 there is an element of infinite order,
there is an element of infinite order,  contains a Kronecker set which is homeomorphic to a Cantor set. If
contains a Kronecker set which is homeomorphic to a Cantor set. If 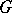 is a non-discrete locally compact Abelian group and if there exists a neighbourhood of the unit element without elements of infinite order,
is a non-discrete locally compact Abelian group and if there exists a neighbourhood of the unit element without elements of infinite order, 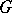 contains
contains  (for some
(for some 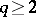 ) as a closed subgroup; any group
) as a closed subgroup; any group  contains a
contains a 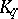 -set which is homeomorphic to a Cantor set.
-set which is homeomorphic to a Cantor set.
In finite-dimensional metrizable locally compact Abelian groups an independent set is a totally-disconnected set. An infinite-dimensional torus contains a Kronecker set homeomorphic to a segment. A union of two Kronecker sets on the circle may prove to be an independent set that is not a Kronecker set. By adding one point to some Kronecker set on an infinite-dimensional torus it is possible to obtain an independent set that is not a Kronecker set. If 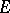 is a compact Kronecker set in
is a compact Kronecker set in 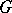 and
and 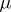 is a bounded measure concentrated on
is a bounded measure concentrated on 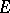 , then
, then
 |
Another important class of subsets of locally compact Abelian groups are Helson sets: Compact sets 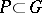 distinguished by the fact that every continuous function
distinguished by the fact that every continuous function 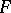 on
on 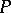 is the restriction to
is the restriction to  of some element of the algebra
of some element of the algebra  . Any compact Kronecker set and any compact
. Any compact Kronecker set and any compact  -set in
-set in 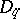 are Helson sets. Not every compact subset of a locally compact Abelian group
are Helson sets. Not every compact subset of a locally compact Abelian group 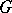 is a Helson set; there exist independent Cantor sets that are not Helson sets. A compact subset
is a Helson set; there exist independent Cantor sets that are not Helson sets. A compact subset  will be a Helson set if and only if
will be a Helson set if and only if  and
and 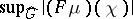 are equivalent norms on the Banach space
are equivalent norms on the Banach space 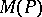 of bounded measures on
of bounded measures on 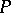 . Let
. Let 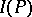 denote the set of all
denote the set of all 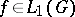 for which
for which 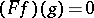 for all
for all 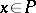 .
. 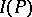 is then a closed ideal in
is then a closed ideal in 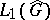 . The space dual to
. The space dual to 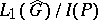 is isometric to the space
is isometric to the space 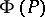 consisting of all
consisting of all 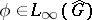 for which
for which
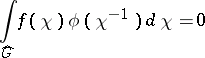 |
for any 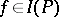 . A compact set
. A compact set  is a Helson set if and only if any function
is a Helson set if and only if any function 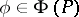 is almost-everywhere equal to the Fourier transform of some bounded measure concentrated on
is almost-everywhere equal to the Fourier transform of some bounded measure concentrated on 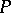 . If
. If 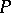 is a Helson set in
is a Helson set in 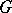 and if
and if 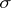 is a non-zero measure concentrated on
is a non-zero measure concentrated on  , then
, then 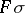 does not tend to zero at infinity.
does not tend to zero at infinity.
In the study of Fourier series on Abelian compact groups the concept of a Sidon set in discrete Abelian groups is very important. Let 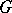 be a compact Abelian group and let
be a compact Abelian group and let  be a subset of
be a subset of  . A function
. A function  is called an
is called an 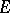 -function if
-function if 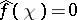 for all
for all 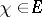 . A linear combination
. A linear combination 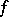 of unitary characters on
of unitary characters on  is called an
is called an  -polynomial if
-polynomial if 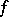 is an
is an 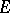 -function. A set
-function. A set 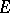 is called a Sidon set if there exists a constant
is called a Sidon set if there exists a constant 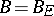 such that
such that
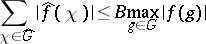 |
for any 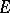 -polynomial on
-polynomial on 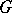 . The following assertions are equivalent:
. The following assertions are equivalent:
a) 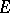 is a Sidon set in
is a Sidon set in 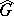 ;
;
b) for any bounded  -function
-function 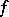 the series
the series 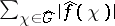 is convergent;
is convergent;
c) for any continuous 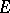 -function
-function 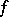 the series
the series 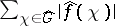 is convergent;
is convergent;
d) any bounded function 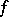 on
on  coincides with the restriction of some element
coincides with the restriction of some element  to
to  ;
;
e) any function on  which tends to zero at infinity coincides with the restriction of some function
which tends to zero at infinity coincides with the restriction of some function  to
to 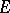 .
.
Any infinite set in  contains an infinite Sidon set. Any independent subset in
contains an infinite Sidon set. Any independent subset in  is a Sidon set.
is a Sidon set.
Another field of abstract harmonic analysis, which at the time of writing is undergoing intensive development, is the theory of closed ideals in  , in particular the theory of spectral synthesis. The problem of spectral synthesis may be posed in a general manner as follows. Let
, in particular the theory of spectral synthesis. The problem of spectral synthesis may be posed in a general manner as follows. Let 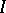 be a closed ideal in
be a closed ideal in  ; the problem is to clarify the conditions under which
; the problem is to clarify the conditions under which 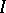 is the intersection of the maximal ideals in
is the intersection of the maximal ideals in 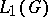 containing
containing 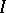 (it should be noted in this context that any maximal ideal in
(it should be noted in this context that any maximal ideal in 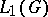 is regular, i.e. closed). One of the most important results of the theory of spectral synthesis is the Wiener Tauberian theorem: If
is regular, i.e. closed). One of the most important results of the theory of spectral synthesis is the Wiener Tauberian theorem: If 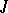 is a closed ideal in
is a closed ideal in 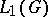 ,
, 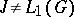 , then there exists a character
, then there exists a character 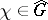 such that
such that 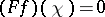 for all
for all  . This theorem may be regarded as a positive solution of the problem stated above for the case
. This theorem may be regarded as a positive solution of the problem stated above for the case 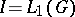 . If every closed ideal in
. If every closed ideal in 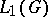 is the intersection of the maximal ideals in which it is contained, one says that
is the intersection of the maximal ideals in which it is contained, one says that 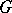 satisfies spectral synthesis. A compact group satisfies spectral synthesis. On the other hand, the following theorem [15] is valid: If the group
satisfies spectral synthesis. A compact group satisfies spectral synthesis. On the other hand, the following theorem [15] is valid: If the group 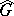 is non-discrete,
is non-discrete, 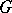 does not satisfy spectral synthesis. It follows that if
does not satisfy spectral synthesis. It follows that if 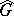 is non-discrete, then the algebra
is non-discrete, then the algebra 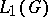 has non-symmetric closed ideals.
has non-symmetric closed ideals.
Abstract harmonic analysis on compact groups may be regarded as part of the theory of representations of compact groups; this theory is closely connected with the theory of almost-periodic functions on groups; see also Bohr compactification and the reviews in [11], [4]. The problems of abstract harmonic analysis on an arbitrary locally compact topological group are much more complicated, in view of the insufficient development and complexity of the general theory of infinite-dimensional representations (cf. Infinite-dimensional representation) of a locally compact group. However, even in such a case the Fourier integral can be defined on a locally compact group [5] and it is possible to obtain analogues of the generalized Bochner theorem, the Plancherel formula and a number of other general theorems [8], [11].
References
| [1] | F. Peter, H. Weyl, "Die Vollständigkeit der primitiven Darstellungen einer geschlossener kontinuierlichen Gruppe" Math. Ann. , 97 (1927) pp. 737–755 |
| [2] | L.S. Pontryagin, "The theory of commutative topological groups" Ann. of Math. (2) , 35 : 2 (1934) pp. 361–388 (In Russian) |
| [3] | E.R. van Kampen, Proc. Nat. Acad. Sci. USA , 20 (1934) pp. 434–436 |
| [4] | A. Weil, "l'Intégration dans les groupes topologiques et ses applications" , Hermann (1940) |
| [5] | I.M. Gel'fand, D.A. Raikov, "Nondegenerate unitary representations of locally (bi)compact groups" Mat. Sb. , 13 (55) (1943) pp. 301–316 (In Russian) (English abstract) |
| [6] | D.A. Raikov, "Harmonic analysis on commutative groups with the Haar measure and character theory" Trudy Mat. Inst. Steklov. , 14 (1945) pp. 1–86 (In Russian) (English abstract) |
| [7] | I.M. [I.M. Gel'fand] Gelfand, D.A. [D.A. Raikov] Raikov, G.E. [G.E. Shilov] Schilow, "Kommutative Normierte Ringe" , Deutsch. Verlag Wissenschaft. (1964) (Translated from Russian) |
| [8] | M.A. Naimark, "Normed rings" , Reidel (1984) (Translated from Russian) |
| [9] | L.S. Pontryagin, "Topological groups" , Princeton Univ. Press (1958) (Translated from Russian) |
| [10] | N. Bourbaki, "Elements of mathematics. Spectral theories" , Addison-Wesley (1977) (Translated from French) |
| [11] | J. Dixmier, " algebras" , North-Holland (1977) (Translated from French) algebras" , North-Holland (1977) (Translated from French) |
| [12] | H., et al. Helson, "The functions which operate on Fourier transforms" Acta Math. , 102 (1959) pp. 135–157 |
| [13] | E. Hewitt, K.A. Ross, "Abstract harmonic analysis" , 1–2 , Springer (1963–1970) |
| [14] | L.H. Loomis, "An introduction to abstract harmonic analysis" , v. Nostrand (1953) |
| [15] | P. Malliavin, "Impossibilité de la synthèse spectrale sur les groupes abéliens non compacts" Publ. Math. IHES , 2 (1959) pp. 61–68 |
| [16] | M.G. Krein, "Sur une généralisation du théorème de Plancherel au cas des intégrales de Fourier sur les groupes topologiques commutatifs" Dokl. Akad. Nauk SSSR , 30 (1941) pp. 484–488 |
Comments
In the theory of thin sets an important type of problem is the question whether the union of two (or, occasionally, of countably many) sets of a certain type is again a set of that type. S.W. Drury proved [a1] that the union of two Sidon sets is again a Sidon set, and N.Th. Varopoulos [a2], using Drury's technique, proved the analogous result for Helson sets. For sets of spectral synthesis the problem is still (1989) not solved.
References
| [a1] | S.W. Drury, "Sur les ensembles de Sidon" C.R. Acad. Sci. Paris , A271 (1970) pp. 162–163 |
| [a2] | N.Th. Varopoulos, "Sur la réunion de deux ensembles de Helson" C.R. Acad. Sci. Paris , A271 (1970) pp. 251–253 |
| [a3] | W. Rudin, "Fourier analysis on groups" , Wiley (1962) |
| [a4] | H. Reiter, "Classical harmonic analysis and locally compact groups" , Clarendon Press (1968) |
| [a5] | L.-Å. Lindahl, F. Poulsen, "Thin sets in harmonic analysis" , M. Dekker (1971) |
| [a6] | C.C. Graham, O.C. McGehee, "Essays in commutative harmonic analysis" , Springer (1979) pp. Chapt. 5 |
| [a7] | J. López, K. Ross, "Sidon sets" , M. Dekker (1975) |
Harmonic analysis, abstract. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Harmonic_analysis,_abstract&oldid=44959