Difference between revisions of "Colombeau generalized function algebras"
(Importing text file) |
m (latex details) |
||
| (3 intermediate revisions by one other user not shown) | |||
| Line 1: | Line 1: | ||
| − | + | <!--This article has been texified automatically. Since there was no Nroff source code for this article, | |
| + | the semi-automatic procedure described at https://encyclopediaofmath.org/wiki/User:Maximilian_Janisch/latexlist | ||
| + | was used. | ||
| + | If the TeX and formula formatting is correct and if all png images have been replaced by TeX code, please remove this message and the {{TEX|semi-auto}} category. | ||
| − | <table class="eq" style="width:100%;"> <tr><td | + | Out of 77 formulas, 75 were replaced by TEX code.--> |
| + | |||
| + | {{TEX|semi-auto}}{{TEX|part}} | ||
| + | Let $\Omega$ be an open subset of ${\bf R} ^ { n }$, and let $\mathcal{D} ( \Omega )$ be the algebra of compactly supported smooth functions. In the original definition, J.F. Colombeau [[#References|[a2]]] started from the space $\mathcal{C} ^ { \infty } ( \mathcal{D} ( \Omega ) )$ of infinitely Silva-differentiable mappings from $\mathcal{D} ( \Omega )$ into $\mathbf{C}$. The space of distributions $\mathcal{D} ^ { \prime } ( \Omega )$ is just the subspace of linear mappings $\mathcal{D} ( \Omega ) \rightarrow \mathbf{C}$. Let | ||
| + | |||
| + | <table class="eq" style="width:100%;"> <tr><td style="width:94%;text-align:center;" valign="top"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c130/c130150/c1301509.png"/></td> </tr></table> | ||
and let | and let | ||
| − | + | \begin{equation*} \varphi _ { \varepsilon , x } ( y ) = \varepsilon ^ { - n } \varphi \left( \frac { y - x } { \varepsilon } \right). \end{equation*} | |
| − | The subalgebra | + | The subalgebra $\mathcal{E} _ { M } ( \mathcal{D} ( \Omega ) )$ is defined by those members $R$ such that for all compact subsets $K \subset \Omega$ and for all multi-indices $\alpha \in {\bf N} _ { 0 } ^ { n }$ there is an $N \in \mathbf{N}$ such that for all $\varphi \in \mathcal{A} _ { N } ( \mathbf{R} ^ { n } )$, the supremum of $| \partial ^ { \alpha } R ( \varphi _ { \varepsilon , x } ) |$ over $x \in K$ is of order $O ( \varepsilon ^ { - N } )$ as $\varepsilon \rightarrow 0$. The ideal $\mathcal{N} ( \mathcal{D} ( \Omega ) )$ is defined by those members $R$ such that for all compact subsets $K \subset \Omega$ and all $\alpha \in {\bf N} _ { 0 } ^ { n }$ there is an $N \in \mathbf{N}$ such that for all $q \geq N$ and $\varphi \in \mathcal{A} _ { q } ( \mathbf{R} ^ { n } )$, the supremum of $| \partial ^ { \alpha } R ( \varphi _ { \varepsilon , x } ) |$ over $x \in K$ is of order $O ( \varepsilon ^ { q - N } )$ as $\varepsilon \rightarrow 0$. The Colombeau generalized function algebra is the factor algebra $\mathcal{E} _ { M } ( \mathcal{D} ( \Omega ) ) / \mathcal{N} ( \mathcal{D} ( \Omega ) )$. It contains the space of distributions $\mathcal{D} ^ { \prime } ( \Omega )$ with derivatives faithfully extended (cf. also [[Generalized function, derivative of a|Generalized function, derivative of a]]). The asymptotic decay property expressed in $\mathcal{N} ( \mathcal{D} ( \Omega ) )$ together with an argument using Taylor expansion shows that $\mathcal{C} ^ { \infty } ( \Omega )$ is a faithful subalgebra. |
| − | Later, Colombeau [[#References|[a3]]], [[#References|[a4]]] replaced the construction by a reduced power of | + | Later, Colombeau [[#References|[a3]]], [[#References|[a4]]] replaced the construction by a reduced power of $\mathcal{C} ^ { \infty } ( \Omega )$ with index set $\Lambda = ( 0 , \infty )$: Let ${ \cal E} _ { M } ( \Omega )$ be the algebra of all nets $( u _ { \varepsilon } ) _ { \varepsilon > 0 } \subset \mathcal{C} ^ { \infty } ( \Omega )$ such that for all compact subsets $K \subset \Omega$ and all multi-indices $\alpha \in {\bf N} _ { 0 } ^ { n }$ there is an $N > 0$ such that the supremum of $| \partial ^ { \alpha } u _ { \varepsilon } ( x ) |$ over $x \in K$ is of order $O ( \varepsilon ^ { - N } )$ as $\varepsilon \rightarrow 0$ (cf. also [[Net (directed set)|Net (directed set)]]). Let $\mathcal{N} ( \Omega )$ be the ideal therein given by those $( u _ { \varepsilon } ) _ { \varepsilon > 0 }$ such that for all compact subsets $K \subset \Omega$, all $\alpha \in {\bf N} _ { 0 } ^ { n }$ and all $q \geq 0$, the supremum of $| \partial ^ { \alpha } u _ { \varepsilon } ( x ) |$ over $x \in K$ is of order $O ( \varepsilon ^ { q } )$ as $\varepsilon \rightarrow 0$. Then set $\mathcal{G} ( \Omega ) = \mathcal{E} _ { M } ( \Omega ) / \mathcal{N} ( \Omega )$. There exist versions with the infinite-order [[Sobolev space|Sobolev space]] $W ^ { \infty , p } ( \Omega )$ in the place of $\mathcal{C} ^ { \infty } ( \Omega )$, $1 \leq p \leq \infty$, or with other topological algebras. |
| − | It is possible to enlarge the class of mollifiers (hence the index set | + | It is possible to enlarge the class of mollifiers (hence the index set $\Lambda$ in the reduced power construction) to produce a version for which smooth coordinate changes commute with the imbedding of distributions. This way Colombeau generalized functions can be defined intrinsically on manifolds. Generalized stochastic processes with paths in $\mathcal{G} ( \Omega )$ have been introduced as well. |
| − | The subalgebra | + | The subalgebra $\mathcal{G} ^ { \infty } ( \Omega )$ is defined by interchanging quantifiers: For all compact sets $K \subset \Omega$ there is an $N > 0$ such that for all $\alpha \in {\bf N} _ { 0 } ^ { n }$, the supremum of $| \partial ^ { \alpha } u _ { \varepsilon } ( x ) |$ on $K$ is of order $O ( \varepsilon ^ { - N } )$ as $\varepsilon \rightarrow 0$. One has that $\mathcal{G} ^ { \infty } ( \Omega ) \cap \mathcal{D} ^ { \prime } ( \Omega ) = \mathcal{C} ^ { \infty } ( \Omega )$, and $\mathcal{G} ^ { \infty } ( \Omega )$ plays the same role in regularity theory here as $C ^ { \infty } ( \Omega )$ does in distribution theory (for example, $u \in \mathcal{G} ( \Omega )$ and $\Delta u \in \mathcal{G} ^ { \infty } ( \Omega )$ implies $u \in \mathcal{G} ^ { \infty } ( \Omega )$, where $\Delta$ denotes the [[Laplace operator|Laplace operator]]). |
For applications in a variety of fields of non-linear analysis and physics, see [[#References|[a1]]], [[#References|[a4]]], [[#References|[a5]]], [[#References|[a6]]], [[#References|[a7]]]. | For applications in a variety of fields of non-linear analysis and physics, see [[#References|[a1]]], [[#References|[a4]]], [[#References|[a5]]], [[#References|[a6]]], [[#References|[a7]]]. | ||
| − | See also [[ | + | See also [[Generalized function algebras]]. |
====References==== | ====References==== | ||
| − | <table>< | + | <table> |
| + | <tr><td valign="top">[a1]</td> <td valign="top"> H.A. Biagioni, "A nonlinear theory of generalized functions" , Springer (1990)</td></tr><tr><td valign="top">[a2]</td> <td valign="top"> J.F. Colombeau, "New generalized functions and multiplication of distributions" , North-Holland (1984)</td></tr><tr><td valign="top">[a3]</td> <td valign="top"> J.F. Colombeau, "Elementary introduction to new generalized functions" , North-Holland (1985)</td></tr><tr><td valign="top">[a4]</td> <td valign="top"> J.F. Colombeau, "Multiplication of distributions. A tool in mathematics, numerical engineering and theoretical physics" , Springer (1992)</td></tr><tr><td valign="top">[a5]</td> <td valign="top"> "Nonlinear theory of generalized functions" M. Grosser (ed.) G. Hörmann (ed.) M. Kunzinger (ed.) M. Oberguggenberger (ed.) , Chapman and Hall/CRC (1999)</td></tr><tr><td valign="top">[a6]</td> <td valign="top"> M. Nedeljkov, S. Pilipović, D. Scarpalézos, "The linear theory of Colombeau generalized functions" , Longman (1998)</td></tr><tr><td valign="top">[a7]</td> <td valign="top"> M. Oberguggenberger, "Multiplication of distributions and applications to partial differential equations" , Longman (1992)</td></tr> | ||
| + | </table> | ||
Latest revision as of 20:13, 4 February 2024
Let $\Omega$ be an open subset of ${\bf R} ^ { n }$, and let $\mathcal{D} ( \Omega )$ be the algebra of compactly supported smooth functions. In the original definition, J.F. Colombeau [a2] started from the space $\mathcal{C} ^ { \infty } ( \mathcal{D} ( \Omega ) )$ of infinitely Silva-differentiable mappings from $\mathcal{D} ( \Omega )$ into $\mathbf{C}$. The space of distributions $\mathcal{D} ^ { \prime } ( \Omega )$ is just the subspace of linear mappings $\mathcal{D} ( \Omega ) \rightarrow \mathbf{C}$. Let
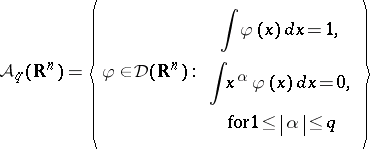 |
and let
\begin{equation*} \varphi _ { \varepsilon , x } ( y ) = \varepsilon ^ { - n } \varphi \left( \frac { y - x } { \varepsilon } \right). \end{equation*}
The subalgebra $\mathcal{E} _ { M } ( \mathcal{D} ( \Omega ) )$ is defined by those members $R$ such that for all compact subsets $K \subset \Omega$ and for all multi-indices $\alpha \in {\bf N} _ { 0 } ^ { n }$ there is an $N \in \mathbf{N}$ such that for all $\varphi \in \mathcal{A} _ { N } ( \mathbf{R} ^ { n } )$, the supremum of $| \partial ^ { \alpha } R ( \varphi _ { \varepsilon , x } ) |$ over $x \in K$ is of order $O ( \varepsilon ^ { - N } )$ as $\varepsilon \rightarrow 0$. The ideal $\mathcal{N} ( \mathcal{D} ( \Omega ) )$ is defined by those members $R$ such that for all compact subsets $K \subset \Omega$ and all $\alpha \in {\bf N} _ { 0 } ^ { n }$ there is an $N \in \mathbf{N}$ such that for all $q \geq N$ and $\varphi \in \mathcal{A} _ { q } ( \mathbf{R} ^ { n } )$, the supremum of $| \partial ^ { \alpha } R ( \varphi _ { \varepsilon , x } ) |$ over $x \in K$ is of order $O ( \varepsilon ^ { q - N } )$ as $\varepsilon \rightarrow 0$. The Colombeau generalized function algebra is the factor algebra $\mathcal{E} _ { M } ( \mathcal{D} ( \Omega ) ) / \mathcal{N} ( \mathcal{D} ( \Omega ) )$. It contains the space of distributions $\mathcal{D} ^ { \prime } ( \Omega )$ with derivatives faithfully extended (cf. also Generalized function, derivative of a). The asymptotic decay property expressed in $\mathcal{N} ( \mathcal{D} ( \Omega ) )$ together with an argument using Taylor expansion shows that $\mathcal{C} ^ { \infty } ( \Omega )$ is a faithful subalgebra.
Later, Colombeau [a3], [a4] replaced the construction by a reduced power of $\mathcal{C} ^ { \infty } ( \Omega )$ with index set $\Lambda = ( 0 , \infty )$: Let ${ \cal E} _ { M } ( \Omega )$ be the algebra of all nets $( u _ { \varepsilon } ) _ { \varepsilon > 0 } \subset \mathcal{C} ^ { \infty } ( \Omega )$ such that for all compact subsets $K \subset \Omega$ and all multi-indices $\alpha \in {\bf N} _ { 0 } ^ { n }$ there is an $N > 0$ such that the supremum of $| \partial ^ { \alpha } u _ { \varepsilon } ( x ) |$ over $x \in K$ is of order $O ( \varepsilon ^ { - N } )$ as $\varepsilon \rightarrow 0$ (cf. also Net (directed set)). Let $\mathcal{N} ( \Omega )$ be the ideal therein given by those $( u _ { \varepsilon } ) _ { \varepsilon > 0 }$ such that for all compact subsets $K \subset \Omega$, all $\alpha \in {\bf N} _ { 0 } ^ { n }$ and all $q \geq 0$, the supremum of $| \partial ^ { \alpha } u _ { \varepsilon } ( x ) |$ over $x \in K$ is of order $O ( \varepsilon ^ { q } )$ as $\varepsilon \rightarrow 0$. Then set $\mathcal{G} ( \Omega ) = \mathcal{E} _ { M } ( \Omega ) / \mathcal{N} ( \Omega )$. There exist versions with the infinite-order Sobolev space $W ^ { \infty , p } ( \Omega )$ in the place of $\mathcal{C} ^ { \infty } ( \Omega )$, $1 \leq p \leq \infty$, or with other topological algebras.
It is possible to enlarge the class of mollifiers (hence the index set $\Lambda$ in the reduced power construction) to produce a version for which smooth coordinate changes commute with the imbedding of distributions. This way Colombeau generalized functions can be defined intrinsically on manifolds. Generalized stochastic processes with paths in $\mathcal{G} ( \Omega )$ have been introduced as well.
The subalgebra $\mathcal{G} ^ { \infty } ( \Omega )$ is defined by interchanging quantifiers: For all compact sets $K \subset \Omega$ there is an $N > 0$ such that for all $\alpha \in {\bf N} _ { 0 } ^ { n }$, the supremum of $| \partial ^ { \alpha } u _ { \varepsilon } ( x ) |$ on $K$ is of order $O ( \varepsilon ^ { - N } )$ as $\varepsilon \rightarrow 0$. One has that $\mathcal{G} ^ { \infty } ( \Omega ) \cap \mathcal{D} ^ { \prime } ( \Omega ) = \mathcal{C} ^ { \infty } ( \Omega )$, and $\mathcal{G} ^ { \infty } ( \Omega )$ plays the same role in regularity theory here as $C ^ { \infty } ( \Omega )$ does in distribution theory (for example, $u \in \mathcal{G} ( \Omega )$ and $\Delta u \in \mathcal{G} ^ { \infty } ( \Omega )$ implies $u \in \mathcal{G} ^ { \infty } ( \Omega )$, where $\Delta$ denotes the Laplace operator).
For applications in a variety of fields of non-linear analysis and physics, see [a1], [a4], [a5], [a6], [a7].
See also Generalized function algebras.
References
| [a1] | H.A. Biagioni, "A nonlinear theory of generalized functions" , Springer (1990) |
| [a2] | J.F. Colombeau, "New generalized functions and multiplication of distributions" , North-Holland (1984) |
| [a3] | J.F. Colombeau, "Elementary introduction to new generalized functions" , North-Holland (1985) |
| [a4] | J.F. Colombeau, "Multiplication of distributions. A tool in mathematics, numerical engineering and theoretical physics" , Springer (1992) |
| [a5] | "Nonlinear theory of generalized functions" M. Grosser (ed.) G. Hörmann (ed.) M. Kunzinger (ed.) M. Oberguggenberger (ed.) , Chapman and Hall/CRC (1999) |
| [a6] | M. Nedeljkov, S. Pilipović, D. Scarpalézos, "The linear theory of Colombeau generalized functions" , Longman (1998) |
| [a7] | M. Oberguggenberger, "Multiplication of distributions and applications to partial differential equations" , Longman (1992) |
Colombeau generalized function algebras. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Colombeau_generalized_function_algebras&oldid=17873