Colombeau generalized function algebras

Let $\Omega$ be an open subset of ${\bf R} ^ { n }$, and let $\mathcal{D} ( \Omega )$ be the algebra of compactly supported smooth functions. In the original definition, J.F. Colombeau [a2] started from the space $\mathcal{C} ^ { \infty } ( \mathcal{D} ( \Omega ) )$ of infinitely Silva-differentiable mappings from $\mathcal{D} ( \Omega )$ into $\mathbf{C}$. The space of distributions $\mathcal{D} ^ { \prime } ( \Omega )$ is just the subspace of linear mappings $\mathcal{D} ( \Omega ) \rightarrow \mathbf{C}$. Let

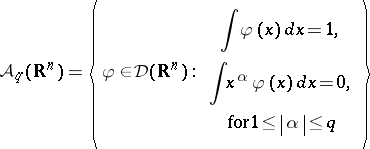and let

$$\begin{equation*} \varphi _ { \varepsilon , x } ( y ) = \varepsilon ^ { - n } \varphi \left( \frac { y - x } { \varepsilon } \right). \end{equation*}$$

The subalgebra $\mathcal{E} _ { M } ( \mathcal{D} ( \Omega ) )$ is defined by those members $R$ such that for all compact subsets $K \subset \Omega$ and for all multi-indices $\alpha \in {\bf N} _ { 0 } ^ { n }$ there is an $N \in \mathbf{N}$ such that for all $\varphi \in \mathcal{A} _ { N } ( \mathbf{R} ^ { n } )$, the supremum of $| \partial ^ { \alpha } R ( \varphi _ { \varepsilon , x } ) |$ over $x \in K$ is of order $O ( \varepsilon ^ { - N } )$ as $\varepsilon \rightarrow 0$. The ideal $\mathcal{N} ( \mathcal{D} ( \Omega ) )$ is defined by those members $R$ such that for all compact subsets $K \subset \Omega$ and all $\alpha \in {\bf N} _ { 0 } ^ { n }$ there is an $N \in \mathbf{N}$ such that for all $q \geq N$ and $\varphi \in \mathcal{A} _ { q } ( \mathbf{R} ^ { n } )$, the supremum of $| \partial ^ { \alpha } R ( \varphi _ { \varepsilon , x } ) |$ over $x \in K$ is of order $O ( \varepsilon ^ { q - N } )$ as $\varepsilon \rightarrow 0$. The Colombeau generalized function algebra is the factor algebra $\mathcal{E} _ { M } ( \mathcal{D} ( \Omega ) ) / \mathcal{N} ( \mathcal{D} ( \Omega ) )$. It contains the space of distributions $\mathcal{D} ^ { \prime } ( \Omega )$ with derivatives faithfully extended (cf. also Generalized function, derivative of a). The asymptotic decay property expressed in $\mathcal{N} ( \mathcal{D} ( \Omega ) )$ together with an argument using Taylor expansion shows that $\mathcal{C} ^ { \infty } ( \Omega )$ is a faithful subalgebra.

Later, Colombeau [a3], [a4] replaced the construction by a reduced power of $\mathcal{C} ^ { \infty } ( \Omega )$ with index set $\Lambda = ( 0 , \infty )$: Let ${ \cal E} _ { M } ( \Omega )$ be the algebra of all nets $( u _ { \varepsilon } ) _ { \varepsilon > 0 } \subset \mathcal{C} ^ { \infty } ( \Omega )$ such that for all compact subsets $K \subset \Omega$ and all multi-indices $\alpha \in {\bf N} _ { 0 } ^ { n }$ there is an $N > 0$ such that the supremum of $| \partial ^ { \alpha } u _ { \varepsilon } ( x ) |$ over $x \in K$ is of order $O ( \varepsilon ^ { - N } )$ as $\varepsilon \rightarrow 0$ (cf. also Net (directed set)). Let $\mathcal{N} ( \Omega )$ be the ideal therein given by those $( u _ { \varepsilon } ) _ { \varepsilon > 0 }$ such that for all compact subsets $K \subset \Omega$, all $\alpha \in {\bf N} _ { 0 } ^ { n }$ and all $q \geq 0$, the supremum of $| \partial ^ { \alpha } u _ { \varepsilon } ( x ) |$ over $x \in K$ is of order $O ( \varepsilon ^ { q } )$ as $\varepsilon \rightarrow 0$. Then set $\mathcal{G} ( \Omega ) = \mathcal{E} _ { M } ( \Omega ) / \mathcal{N} ( \Omega )$. There exist versions with the infinite-order Sobolev space $W ^ { \infty , p } ( \Omega )$ in the place of $\mathcal{C} ^ { \infty } ( \Omega )$, $1 \leq p \leq \infty$, or with other topological algebras.

It is possible to enlarge the class of mollifiers (hence the index set $\Lambda$ in the reduced power construction) to produce a version for which smooth coordinate changes commute with the imbedding of distributions. This way Colombeau generalized functions can be defined intrinsically on manifolds. Generalized stochastic processes with paths in $\mathcal{G} ( \Omega )$ have been introduced as well.

The subalgebra $\mathcal{G} ^ { \infty } ( \Omega )$ is defined by interchanging quantifiers: For all compact sets $K \subset \Omega$ there is an $N > 0$ such that for all $\alpha \in {\bf N} _ { 0 } ^ { n }$, the supremum of $| \partial ^ { \alpha } u _ { \varepsilon } ( x ) |$ on $K$ is of order $O ( \varepsilon ^ { - N } )$ as $\varepsilon \rightarrow 0$. One has that $\mathcal{G} ^ { \infty } ( \Omega ) \cap \mathcal{D} ^ { \prime } ( \Omega ) = \mathcal{C} ^ { \infty } ( \Omega )$, and $\mathcal{G} ^ { \infty } ( \Omega )$ plays the same role in regularity theory here as $C ^ { \infty } ( \Omega )$ does in distribution theory (for example, $u \in \mathcal{G} ( \Omega )$ and $\Delta u \in \mathcal{G} ^ { \infty } ( \Omega )$ implies $u \in \mathcal{G} ^ { \infty } ( \Omega )$, where $\Delta$ denotes the Laplace operator).

For applications in a variety of fields of non-linear analysis and physics, see [a1], [a4], [a5], [a6], [a7].

See also Generalized function algebras.

References

[a1]	H.A. Biagioni, "A nonlinear theory of generalized functions" , Springer (1990)
[a2]	J.F. Colombeau, "New generalized functions and multiplication of distributions" , North-Holland (1984)
[a3]	J.F. Colombeau, "Elementary introduction to new generalized functions" , North-Holland (1985)
[a4]	J.F. Colombeau, "Multiplication of distributions. A tool in mathematics, numerical engineering and theoretical physics" , Springer (1992)
[a5]	"Nonlinear theory of generalized functions" M. Grosser (ed.) G. Hörmann (ed.) M. Kunzinger (ed.) M. Oberguggenberger (ed.) , Chapman and Hall/CRC (1999)
[a6]	M. Nedeljkov, S. Pilipović, D. Scarpalézos, "The linear theory of Colombeau generalized functions" , Longman (1998)
[a7]	M. Oberguggenberger, "Multiplication of distributions and applications to partial differential equations" , Longman (1992)