Difference between revisions of "Wild sphere"
From Encyclopedia of Mathematics
(Importing text file) |
|||
| (One intermediate revision by one other user not shown) | |||
| Line 1: | Line 1: | ||
| − | A closed manifold in Euclidean three-space | + | {{TEX|done}} |
| + | A closed manifold in Euclidean three-space $E^3$ obtained by a [[wild imbedding]] of the sphere $S^2$ in $E^3$. Thus, a wild sphere is the sum of two discs with a common boundary, which is a [[wild knot]]. The first example of a wild sphere is the so-called "horned sphere of Alexander", horned sphere or Alexander sphere (Fig. a); it bounds a domain which is not homeomorphic to $E^3$ (in the figure this is the interior of the cylinder without any interlinking handles and points forming their boundary). Fig. b shows a wild sphere in which the exterior domain alone is not homeomorphic to $E^3$. | ||
<img style="border:1px solid;" src="https://www.encyclopediaofmath.org/legacyimages/common_img/w097990a.gif" /> | <img style="border:1px solid;" src="https://www.encyclopediaofmath.org/legacyimages/common_img/w097990a.gif" /> | ||
| Line 10: | Line 11: | ||
====References==== | ====References==== | ||
| − | <table><TR><TD valign="top">[1]</TD> <TD valign="top"> L.V. Keldysh, "Topological imbeddings in Euclidean space" ''Proc. Steklov Inst. Math.'' , '''81''' (1968) ''Trudy Mat. Inst. Akad. Nauk. SSSR'' , '''81''' (1966)</TD></TR></table> | + | <table> |
| + | <TR><TD valign="top">[1]</TD> <TD valign="top"> L.V. Keldysh, "Topological imbeddings in Euclidean space" ''Proc. Steklov Inst. Math.'' , '''81''' (1968) ''Trudy Mat. Inst. Akad. Nauk. SSSR'' , '''81''' (1966)</TD></TR> | ||
| + | <TR><TD valign="top">[a1]</TD> <TD valign="top"> R.H. Bing, "The geometric topology of $3$-manifolds" , Amer. Math. Soc. (1983)</TD></TR><TR><TD valign="top">[a2]</TD> <TD valign="top"> E.E. Moise, "Geometric topology in dimensions 2 and 3" , Springer (1977)</TD></TR> | ||
| + | </table> | ||
| − | + | {{OldImage}} | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
Latest revision as of 08:35, 1 May 2023
A closed manifold in Euclidean three-space $E^3$ obtained by a wild imbedding of the sphere $S^2$ in $E^3$. Thus, a wild sphere is the sum of two discs with a common boundary, which is a wild knot. The first example of a wild sphere is the so-called "horned sphere of Alexander", horned sphere or Alexander sphere (Fig. a); it bounds a domain which is not homeomorphic to $E^3$ (in the figure this is the interior of the cylinder without any interlinking handles and points forming their boundary). Fig. b shows a wild sphere in which the exterior domain alone is not homeomorphic to $E^3$.
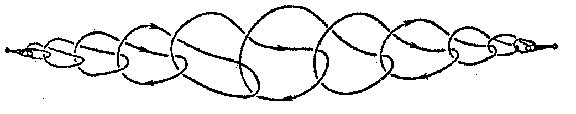
Figure: w097990a
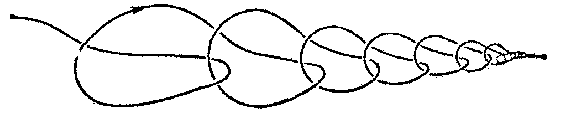
Figure: w097990b
References
| [1] | L.V. Keldysh, "Topological imbeddings in Euclidean space" Proc. Steklov Inst. Math. , 81 (1968) Trudy Mat. Inst. Akad. Nauk. SSSR , 81 (1966) |
| [a1] | R.H. Bing, "The geometric topology of $3$-manifolds" , Amer. Math. Soc. (1983) |
| [a2] | E.E. Moise, "Geometric topology in dimensions 2 and 3" , Springer (1977) |
🛠️ This page contains images that should be replaced by better images in the SVG file format. 🛠️
How to Cite This Entry:
Wild sphere. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Wild_sphere&oldid=16644
Wild sphere. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Wild_sphere&oldid=16644
This article was adapted from an original article by M.I. Voitsekhovskii (originator), which appeared in Encyclopedia of Mathematics - ISBN 1402006098. See original article