|
|
| (4 intermediate revisions by 3 users not shown) |
| Line 1: |
Line 1: |
| − | A [[Linear representation|linear representation]] of the group <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r081/r081470/r0814701.png" /> over a field <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r081/r081470/r0814702.png" />. If <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r081/r081470/r0814703.png" />, then all finite-dimensional representations of the symmetric groups are completely reducible (cf. [[Reducible representation|Reducible representation]]) and defined over <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r081/r081470/r0814704.png" /> (in other words, irreducible finite-dimensional representations over <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r081/r081470/r0814705.png" /> are absolutely irreducible).
| + | <!-- |
| | + | r0814701.png |
| | + | $#A+1 = 224 n = 2 |
| | + | $#C+1 = 224 : ~/encyclopedia/old_files/data/R081/R.0801470 Representation of the symmetric groups |
| | + | Automatically converted into TeX, above some diagnostics. |
| | + | Please remove this comment and the {{TEX|auto}} line below, |
| | + | if TeX found to be correct. |
| | + | --> |
| | | | |
| − | The irreducible finite-dimensional representations of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r081/r081470/r0814706.png" /> over <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r081/r081470/r0814707.png" /> are classified as follows. Let <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r081/r081470/r0814708.png" /> be a [[Young diagram|Young diagram]] corresponding to a partition <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r081/r081470/r0814709.png" /> of the number <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r081/r081470/r08147010.png" />, let <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r081/r081470/r08147011.png" /> (respectively, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r081/r081470/r08147012.png" />) be the subgroup of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r081/r081470/r08147013.png" /> consisting of all permutations mapping each of the numbers <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r081/r081470/r08147014.png" /> into a number in the same row (respectively, column) of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r081/r081470/r08147015.png" />. Then
| + | {{TEX|auto}} |
| | + | {{TEX|done}} |
| | | | |
| − | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r081/r081470/r08147016.png" /></td> </tr></table>
| + | A [[Linear representation|linear representation]] of the group $ S _ {m} $ |
| | + | over a field $ K $. |
| | + | If $ \mathop{\rm char} K = 0 $, |
| | + | then all finite-dimensional representations of the symmetric groups are completely reducible (cf. [[Reducible representation|Reducible representation]]) and defined over $ \mathbf Q $ (in other words, irreducible finite-dimensional representations over $ \mathbf Q $ |
| | + | are absolutely irreducible). |
| | + | |
| | + | The irreducible finite-dimensional representations of $ S _ {m} $ |
| | + | over $ \mathbf Q $ |
| | + | are classified as follows. Let $ d $ |
| | + | be a [[Young diagram|Young diagram]] corresponding to a partition $ \lambda = ( \lambda _ {1} \dots \lambda _ {r} ) $ |
| | + | of the number $ m $, |
| | + | let $ R _ {d} $ (respectively, $ C _ {d} $) |
| | + | be the subgroup of $ S _ {m} $ |
| | + | consisting of all permutations mapping each of the numbers $ 1 \dots m $ |
| | + | into a number in the same row (respectively, column) of $ d $. |
| | + | Then |
| | + | |
| | + | $$ |
| | + | R _ {d} \simeq \ |
| | + | S _ {\lambda _ {1} } |
| | + | \times \dots \times |
| | + | S _ {\lambda _ {r} } |
| | + | $$ |
| | | | |
| | and | | and |
| | | | |
| − | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r081/r081470/r08147017.png" /></td> </tr></table>
| + | $$ |
| | + | C _ {d} \simeq \ |
| | + | S _ {\lambda _ {1} ^ \prime } |
| | + | \times \dots \times |
| | + | S _ {\lambda _ {s} ^ \prime } , |
| | + | $$ |
| | + | |
| | + | where $ \lambda ^ \prime = ( \lambda _ {1} ^ \prime \dots \lambda _ {s} ^ \prime ) $ |
| | + | is the partition of $ m $ |
| | + | dual to $ \lambda $. |
| | + | There exists a unique irreducible representation $ T _ \lambda : S _ {m} \rightarrow \mathop{\rm GL} ( U _ \lambda ) $ |
| | + | of $ S _ {m} $ (depending on $ \lambda $ |
| | + | only) with the following properties: 1) in the space $ U _ \lambda $ |
| | + | there is a non-zero vector $ u _ {d} $ |
| | + | such that $ T _ \lambda ( g) u _ {d} = u _ {d} $ |
| | + | for any $ g \in R _ {d} $; |
| | + | and 2) in $ U _ \lambda $ |
| | + | there exists a non-zero vector $ u _ {d} ^ \prime $ |
| | + | such that $ T _ \lambda ( g) u _ {d} ^ \prime = \epsilon ( g) u _ {d} ^ \prime $ |
| | + | for any $ g \in C _ {d} $, |
| | + | where $ \epsilon ( g) = \pm 1 $ |
| | + | is the parity (sign) of $ g $. |
| | + | Representations corresponding to distinct partitions are not equivalent, and they exhaust all irreducible representations of $ S _ {m} $ |
| | + | over $ Q $. |
| | + | |
| | + | The vectors $ u _ {d} $ |
| | + | and $ u _ {d} ^ \prime $ |
| | + | are defined uniquely up to multiplication by a scalar. For all diagrams corresponding to a partition $ \lambda $ |
| | + | these vectors are normalized such that $ gu _ {d} = u _ {gd} $ |
| | + | and $ gu _ {d} ^ \prime = u _ {gd} ^ \prime $ |
| | + | for any $ g \in S _ {m} $. |
| | + | Here $ gd $ |
| | + | denotes the diagram obtained from $ d $ |
| | + | by applying to all numbers the permutation $ g $. |
| | + | The vectors $ u _ {d} $ (respectively, $ u _ {d} ^ \prime $) |
| | + | corresponding to standard diagrams $ d $ |
| | + | form a basis for $ U _ \lambda $. |
| | + | In this basis the operators of the representation $ T _ \lambda $ |
| | + | have the form of integral matrices. The dimension of $ T _ \lambda $ |
| | + | is |
| | + | |
| | + | $$ |
| | + | \mathop{\rm dim} T _ \lambda = \ |
| | + | |
| | + | \frac{m! \prod _ {i < j } |
| | + | ( l _ {i} - l _ {j} ) }{\prod _ {i} l _ {i} ! } |
| | + | = \ |
| | | | |
| − | where <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r081/r081470/r08147018.png" /> is the partition of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r081/r081470/r08147019.png" /> dual to <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r081/r081470/r08147020.png" />. There exists a unique irreducible representation <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r081/r081470/r08147021.png" /> of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r081/r081470/r08147022.png" /> (depending on <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r081/r081470/r08147023.png" /> only) with the following properties: 1) in the space <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r081/r081470/r08147024.png" /> there is a non-zero vector <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r081/r081470/r08147025.png" /> such that <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r081/r081470/r08147026.png" /> for any <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r081/r081470/r08147027.png" />; and 2) in <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r081/r081470/r08147028.png" /> there exists a non-zero vector <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r081/r081470/r08147029.png" /> such that <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r081/r081470/r08147030.png" /> for any <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r081/r081470/r08147031.png" />, where <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r081/r081470/r08147032.png" /> is the parity (sign) of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r081/r081470/r08147033.png" />. Representations corresponding to distinct partitions are not equivalent, and they exhaust all irreducible representations of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r081/r081470/r08147034.png" /> over <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r081/r081470/r08147035.png" />.
| + | \frac{m! }{\prod _ {( i, j) } \lambda _ {ij} } |
| | + | , |
| | + | $$ |
| | | | |
| − | The vectors <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r081/r081470/r08147036.png" /> and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r081/r081470/r08147037.png" /> are defined uniquely up to multiplication by a scalar. For all diagrams corresponding to a partition <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r081/r081470/r08147038.png" /> these vectors are normalized such that <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r081/r081470/r08147039.png" /> and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r081/r081470/r08147040.png" /> for any <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r081/r081470/r08147041.png" />. Here <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r081/r081470/r08147042.png" /> denotes the diagram obtained from <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r081/r081470/r08147043.png" /> by applying to all numbers the permutation <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r081/r081470/r08147044.png" />. The vectors <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r081/r081470/r08147045.png" /> (respectively, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r081/r081470/r08147046.png" />) corresponding to standard diagrams <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r081/r081470/r08147047.png" /> form a basis for <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r081/r081470/r08147048.png" />. In this basis the operators of the representation <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r081/r081470/r08147049.png" /> have the form of integral matrices. The dimension of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r081/r081470/r08147050.png" /> is
| + | where $ l _ {i} = \lambda _ {i} + r - i $, |
| | + | $ i = 1 \dots r $, |
| | + | and the product in the denominator of the last expression is taken over all cells $ c _ {ij} $ |
| | + | of the Young tableau $ t _ \lambda $; |
| | + | $ \lambda _ {ij} $ |
| | + | denotes the length of the corresponding hook. |
| | | | |
| − | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r081/r081470/r08147051.png" /></td> </tr></table>
| + | To the partition $ ( m) $ |
| | + | corresponds the trivial one-dimensional representation of $ S _ {m} $, |
| | + | while to the partition $ ( 1, \dots, 1) $ |
| | + | corresponds the non-trivial one-dimensional representation $ \epsilon $ (the [[Signature (permutation)|signature]] homomorphism, giving the parity or '''sign representation'''). To the partition $ \lambda ^ \prime $ |
| | + | dual to $ \lambda $ |
| | + | corresponds the representation $ \epsilon T _ \lambda $. |
| | + | The space $ U _ {\lambda ^ \prime } $ |
| | + | can be identified (in a canonical way, up to a [[Homothety|homothety]]) with $ U _ \lambda $, |
| | + | so that $ T _ {\lambda ^ \prime } ( g) = \epsilon ( g) T _ \lambda ( g) $ |
| | + | for any $ g \in S _ {m} $. |
| | + | Moreover, one may take $ u _ {d} ^ \prime = u _ {d ^ \prime } $, |
| | + | where $ d ^ \prime $ |
| | + | is the diagram obtained from $ d $ |
| | + | by transposition. |
| | | | |
| − | where <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r081/r081470/r08147052.png" />, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r081/r081470/r08147053.png" />, and the product in the denominator of the last expression is taken over all cells <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r081/r081470/r08147054.png" /> of the Young tableau <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r081/r081470/r08147055.png" />; <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r081/r081470/r08147056.png" /> denotes the length of the corresponding hook.
| + | The construction of a complete system of irreducible representations of a symmetric group invokes the use of the [[Young symmetrizer]], and allows one to obtain the decomposition of the [[regular representation]]. If $ d $ |
| | + | is the Young diagram corresponding to a partition $ \lambda $, |
| | + | then the representation $ T _ \lambda $ |
| | + | is equivalent to the representation of $ S _ {m} $ |
| | + | in the left ideal of the group algebra $ \mathbf Q S _ {m} $ |
| | + | generated by the Young symmetrizer $ e _ {d} $. |
| | + | An a posteriori description of $ e _ {d} $ |
| | + | is the following: $ T _ \mu ( e _ {d} ) = 0 $ |
| | + | for $ \lambda \neq \mu $, |
| | + | and $ T _ \lambda ( e _ {d} ) $ |
| | + | is the operator, of rank 1, acting by the formula $ T _ \lambda ( e _ {d} ) u = ( u _ {d} , u ) u _ {d} ^ \prime $ |
| | + | for any $ u \in U _ \lambda $. |
| | + | Here $ ( , ) $ |
| | + | denotes the invariant scalar product in $ U _ \lambda $, |
| | + | normalized in a suitable manner. Moreover, |
| | | | |
| − | To the partition <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r081/r081470/r08147057.png" /> corresponds the trivial one-dimensional representation of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r081/r081470/r08147058.png" />, while to the partition <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r081/r081470/r08147059.png" /> corresponds the non-trivial one-dimensional representation <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r081/r081470/r08147060.png" /> (the parity or sign representation). To the partition <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r081/r081470/r08147061.png" /> dual to <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r081/r081470/r08147062.png" /> corresponds the representation <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r081/r081470/r08147063.png" />. The space <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r081/r081470/r08147064.png" /> can be identified (in a canonical way, up to a [[Homothety|homothety]]) with <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r081/r081470/r08147065.png" />, so that <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r081/r081470/r08147066.png" /> for any <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r081/r081470/r08147067.png" />. Moreover, one may take <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r081/r081470/r08147068.png" />, where <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r081/r081470/r08147069.png" /> is the diagram obtained from <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r081/r081470/r08147070.png" /> by transposition.
| + | $$ |
| | + | ( u _ {d} , u _ {d} ^ \prime ) = \ |
| | | | |
| − | The construction of a complete system of irreducible representations of a symmetric group invokes the use of the [[Young symmetrizer|Young symmetrizer]], and allows one to obtain the decomposition of the [[Regular representation|regular representation]]. If <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r081/r081470/r08147071.png" /> is the Young diagram corresponding to a partition <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r081/r081470/r08147072.png" />, then the representation <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r081/r081470/r08147073.png" /> is equivalent to the representation of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r081/r081470/r08147074.png" /> in the left ideal of the group algebra <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r081/r081470/r08147075.png" /> generated by the Young symmetrizer <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r081/r081470/r08147076.png" />. An a posteriori description of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r081/r081470/r08147077.png" /> is the following: <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r081/r081470/r08147078.png" /> for <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r081/r081470/r08147079.png" />, and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r081/r081470/r08147080.png" /> is the operator, of rank 1, acting by the formula <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r081/r081470/r08147081.png" /> for any <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r081/r081470/r08147082.png" />. Here <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r081/r081470/r08147083.png" /> denotes the invariant scalar product in <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r081/r081470/r08147084.png" />, normalized in a suitable manner. Moreover,
| + | \frac{m! }{ \mathop{\rm dim} U _ \lambda } |
| | + | . |
| | + | $$ |
| | | | |
| − | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r081/r081470/r08147085.png" /></td> </tr></table>
| + | The [[Frobenius formula|Frobenius formula]] gives a generating function for the characters of $ T _ \lambda $. |
| | + | However, recurrence relations are more convenient to use when computing individual values of characters. The Murnagan–Nakayama rule is most effective: Let $ a _ {\lambda \mu } = a _ {\lambda \mu } ^ {(m)} $ |
| | + | be the value of a character of $ T _ \lambda $ |
| | + | on the class $ [ \mu ] $ |
| | + | of conjugate elements of $ S _ {m} $ |
| | + | defined by a partition $ \mu $ |
| | + | of $ m $, |
| | + | and suppose that $ \mu $ |
| | + | contains a number $ p $. |
| | + | Denote by $ \overline \mu $ |
| | + | the partition of $ m - p $ |
| | + | obtained from $ \mu $ |
| | + | by deleting $ p $. |
| | + | Then |
| | | | |
| − | The [[Frobenius formula|Frobenius formula]] gives a generating function for the characters of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r081/r081470/r08147086.png" />. However, recurrence relations are more convenient to use when computing individual values of characters. The Murnagan–Nakayama rule is most effective: Let <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r081/r081470/r08147087.png" /> be the value of a character of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r081/r081470/r08147088.png" /> on the class <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r081/r081470/r08147089.png" /> of conjugate elements of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r081/r081470/r08147090.png" /> defined by a partition <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r081/r081470/r08147091.png" /> of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r081/r081470/r08147092.png" />, and suppose that <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r081/r081470/r08147093.png" /> contains a number <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r081/r081470/r08147094.png" />. Denote by <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r081/r081470/r08147095.png" /> the partition of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r081/r081470/r08147096.png" /> obtained from <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r081/r081470/r08147097.png" /> by deleting <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r081/r081470/r08147098.png" />. Then
| + | $$ |
| | + | a _ {\lambda \mu } ^ {(m)} = \ |
| | + | \sum _ {\overline \lambda } |
| | + | (- 1) ^ {i ( \overline \lambda ) } |
| | + | a _ {\overline \lambda \overline \mu } ^ {( m - p) } , |
| | + | $$ |
| | | | |
| − | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r081/r081470/r08147099.png" /></td> </tr></table>
| + | where the sum is over all partitions $ \overline \lambda $ |
| | + | of $ m - p $ |
| | + | obtained by deleting a skew hook of length $ p $ |
| | + | from the [[Young tableau|Young tableau]] $ t _ \lambda $, |
| | + | and where $ i ( \overline \lambda ) $ |
| | + | denotes the height of the skew hook taken out. |
| | | | |
| − | where the sum is over all partitions <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r081/r081470/r081470100.png" /> of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r081/r081470/r081470101.png" /> obtained by deleting a skew hook of length <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r081/r081470/r081470102.png" /> from the [[Young tableau|Young tableau]] <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r081/r081470/r081470103.png" />, and where <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r081/r081470/r081470104.png" /> denotes the height of the skew hook taken out.
| + | There is also a method (cf. [[#References|[5]]]) by which one can find the entire table of characters of $ S _ {m} $, |
| | + | i.e. the matrix $ A = \| a _ {\lambda \mu } \| $. |
| | + | Let $ M _ \lambda $ |
| | + | be the representation of $ S _ {m} $ |
| | + | induced by the trivial one-dimensional representation of the subgroup $ R _ \lambda = R _ {d} $, |
| | + | where $ d $ |
| | + | is the Young diagram corresponding to the partition $ \lambda $. |
| | + | Let $ M _ \lambda = \sum _ \mu m _ {\lambda \mu } T _ \mu $ |
| | + | and $ M = \| m _ {\lambda \mu } \| $. |
| | + | If one assumes that the rows and columns of $ M $ |
| | + | are positioned in order of lexicographically decreasing indices (partitions), then $ M $ |
| | + | is a lower-triangular matrix with 1's on the diagonal. The value of a character of $ M _ \lambda $ |
| | + | on a class $ [ \mu ] $ |
| | + | is equal to |
| | | | |
| − | There is also a method (cf. [[#References|[5]]]) by which one can find the entire table of characters of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r081/r081470/r081470105.png" />, i.e. the matrix <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r081/r081470/r081470106.png" />. Let <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r081/r081470/r081470107.png" /> be the representation of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r081/r081470/r081470108.png" /> induced by the trivial one-dimensional representation of the subgroup <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r081/r081470/r081470109.png" />, where <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r081/r081470/r081470110.png" /> is the Young diagram corresponding to the partition <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r081/r081470/r081470111.png" />. Let <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r081/r081470/r081470112.png" /> and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r081/r081470/r081470113.png" />. If one assumes that the rows and columns of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r081/r081470/r081470114.png" /> are positioned in order of lexicographically decreasing indices (partitions), then <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r081/r081470/r081470115.png" /> is a lower-triangular matrix with 1's on the diagonal. The value of a character of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r081/r081470/r081470116.png" /> on a class <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r081/r081470/r081470117.png" /> is equal to
| + | $$ |
| | + | b _ {\lambda \mu } = \ |
| | | | |
| − | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r081/r081470/r081470118.png" /></td> </tr></table>
| + | \frac{c _ \mu | R _ \lambda \cap [ \mu ] | }{| R _ \lambda | } |
| | + | , |
| | + | $$ |
| | | | |
| − | where <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r081/r081470/r081470119.png" /> is the order of the centralizer of the permutations (a representative) from <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r081/r081470/r081470120.png" />. The matrix <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r081/r081470/r081470121.png" /> is upper triangular, and one has <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r081/r081470/r081470122.png" />, where <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r081/r081470/r081470123.png" />, from which <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r081/r081470/r081470124.png" /> can be uniquely found. Then the matrix <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r081/r081470/r081470125.png" /> is determined by | + | where $ c _ \mu $ |
| | + | is the order of the centralizer of the permutations (a representative) from $ [ \mu ] $. |
| | + | The matrix $ B = \| b _ {\lambda \mu } \| $ |
| | + | is upper triangular, and one has $ MM ^ {T} = BC ^ {-1} B ^ {T} $, |
| | + | where $ C = \mathop{\rm diag} ( c _ \mu ) $, |
| | + | from which $ M $ |
| | + | can be uniquely found. Then the matrix $ A $ |
| | + | is determined by |
| | | | |
| − | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r081/r081470/r081470126.png" /></td> </tr></table>
| + | $$ |
| | + | A = M ^ {-1} B. |
| | + | $$ |
| | | | |
| − | The restriction of a representation <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r081/r081470/r081470127.png" /> of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r081/r081470/r081470128.png" /> to the subgroup <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r081/r081470/r081470129.png" /> can be found by the ramification rule | + | The restriction of a representation $ T _ \lambda $ |
| | + | of $ S _ {m} $ |
| | + | to the subgroup $ S _ {m - 1 } $ |
| | + | can be found by the ramification rule |
| | | | |
| − | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r081/r081470/r081470130.png" /></td> </tr></table>
| + | $$ |
| | + | T _ \lambda \mid _ {S _ {m - 1 } } = \ |
| | + | \sum _ { i } T _ {( \lambda _ {1} \dots \lambda _ {i} - 1 \dots \lambda _ {r} ) } , |
| | + | $$ |
| | | | |
| − | where the summation extends over all <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r081/r081470/r081470131.png" /> for which <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r081/r081470/r081470132.png" /> (including <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r081/r081470/r081470133.png" />). The restriction of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r081/r081470/r081470134.png" /> to the subgroup <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r081/r081470/r081470135.png" /> is absolutely irreducible for <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r081/r081470/r081470136.png" /> and splits for <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r081/r081470/r081470137.png" /> over a quadratic extension of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r081/r081470/r081470138.png" /> into a sum of two non-equivalent absolutely-irreducible representations of equal dimension. The representations of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r081/r081470/r081470139.png" /> thus obtained exhaust all its irreducible representations over <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r081/r081470/r081470140.png" />. | + | where the summation extends over all $ i $ |
| | + | for which $ \lambda _ {i} > \lambda _ {i + 1 } $ (including $ r $). |
| | + | The restriction of $ T _ \lambda $ |
| | + | to the subgroup $ A _ {m} $ |
| | + | is absolutely irreducible for $ \lambda \neq \lambda ^ \prime $ |
| | + | and splits for $ \lambda = \lambda ^ \prime $ |
| | + | over a quadratic extension of $ \mathbf Q $ |
| | + | into a sum of two non-equivalent absolutely-irreducible representations of equal dimension. The representations of $ A _ {m} $ |
| | + | thus obtained exhaust all its irreducible representations over $ \mathbf C $. |
| | | | |
| − | For representations of the symmetric groups in tensors see [[Representation of the classical groups|Representation of the classical groups]]. | + | For representations of the symmetric groups in tensors see [[Representation of the classical groups]]. |
| | | | |
| | The theory of modular representations of the symmetric groups has also been developed (see, e.g. [[#References|[5]]]). | | The theory of modular representations of the symmetric groups has also been developed (see, e.g. [[#References|[5]]]). |
| | | | |
| | ====References==== | | ====References==== |
| − | <table><TR><TD valign="top">[1]</TD> <TD valign="top"> H. Weyl, "The classical groups, their invariants and representations" , Princeton Univ. Press (1946)</TD></TR><TR><TD valign="top">[2]</TD> <TD valign="top"> F.D. Murnagan, "The theory of group representations" , Johns Hopkins Univ. Press (1938)</TD></TR><TR><TD valign="top">[3]</TD> <TD valign="top"> M. Hamermesh, "Group theory and its application to physical problems" , Addison-Wesley (1962)</TD></TR><TR><TD valign="top">[4]</TD> <TD valign="top"> C.W. Curtis, I. Reiner, "Representation theory of finite groups and associative algebras" , Interscience (1962)</TD></TR><TR><TD valign="top">[5]</TD> <TD valign="top"> G.D. James, "The representation theory of the symmetric groups" , Springer (1978)</TD></TR></table> | + | <table><TR><TD valign="top">[1]</TD> <TD valign="top"> H. Weyl, "The classical groups, their invariants and representations" , Princeton Univ. Press (1946) {{MR|0000255}} {{ZBL|1024.20502}} </TD></TR><TR><TD valign="top">[2]</TD> <TD valign="top"> F.D. Murnagan, "The theory of group representations" , Johns Hopkins Univ. Press (1938)</TD></TR><TR><TD valign="top">[3]</TD> <TD valign="top"> M. Hamermesh, "Group theory and its application to physical problems" , Addison-Wesley (1962) {{MR|0136667}} {{ZBL|0100.36704}} </TD></TR><TR><TD valign="top">[4]</TD> <TD valign="top"> C.W. Curtis, I. Reiner, "Representation theory of finite groups and associative algebras" , Interscience (1962) {{MR|0144979}} {{ZBL|0131.25601}} </TD></TR><TR><TD valign="top">[5]</TD> <TD valign="top"> G.D. James, "The representation theory of the symmetric groups" , Springer (1978) {{MR|0513828}} {{ZBL|0393.20009}} </TD></TR></table> |
| − | | |
| − | | |
| | | | |
| | ====Comments==== | | ====Comments==== |
| − | Let <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r081/r081470/r081470141.png" /> be the free Abelian group generated by the complex irreducible representations of the symmetric group on <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r081/r081470/r081470142.png" /> letters, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r081/r081470/r081470143.png" />. Now consider the direct sum | + | Let $ R ( S _ {m} ) $ |
| | + | be the free Abelian group generated by the complex irreducible representations of the symmetric group on $ m $ |
| | + | letters, $ S _ {m} $. |
| | + | Now consider the direct sum |
| | | | |
| − | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r081/r081470/r081470144.png" /></td> </tr></table>
| + | $$ |
| | + | R = \oplus _ { m= 0} ^ \infty R( S _ {m} ) ,\ \ |
| | + | R ( S _ {0} ) = \mathbf Z . |
| | + | $$ |
| | | | |
| − | It is possible to define a [[Hopf algebra|Hopf algebra]] structure on <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r081/r081470/r081470145.png" />, as follows. First the multiplication. Let <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r081/r081470/r081470146.png" /> and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r081/r081470/r081470147.png" /> be, respectively, representations of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r081/r081470/r081470148.png" /> and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r081/r081470/r081470149.png" />. Taking the [[Tensor product|tensor product]] defines a representation <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r081/r081470/r081470150.png" /> of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r081/r081470/r081470151.png" />. Consider <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r081/r081470/r081470152.png" /> as a subgroup of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r081/r081470/r081470153.png" /> in the natural way. The product of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r081/r081470/r081470154.png" /> and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r081/r081470/r081470155.png" /> in <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r081/r081470/r081470156.png" /> is now defined by taking the [[Induced representation|induced representation]] to <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r081/r081470/r081470157.png" />: | + | It is possible to define a [[Hopf algebra|Hopf algebra]] structure on $ R $, |
| | + | as follows. First the multiplication. Let $ \rho $ |
| | + | and $ \tau $ |
| | + | be, respectively, representations of $ S _ {n} $ |
| | + | and $ S _ {m} $. |
| | + | Taking the [[Tensor product|tensor product]] defines a representation $ ( g, h) \mapsto \rho ( g) \otimes \sigma ( h) $ |
| | + | of $ S _ {n} \times S _ {m} $. |
| | + | Consider $ S _ {n} \times S _ {m} $ |
| | + | as a subgroup of $ S _ {n+m} $ |
| | + | in the natural way. The product of $ \rho $ |
| | + | and $ \tau $ |
| | + | in $ R $ |
| | + | is now defined by taking the [[Induced representation|induced representation]] to $ S _ {n+m} $: |
| | | | |
| − | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r081/r081470/r081470158.png" /></td> </tr></table>
| + | $$ |
| | + | \rho \sigma = \mathrm{Ind} _ {S _ {n} \times S _ {m} } ^ {S _ {n+m} } ( \rho \otimes \sigma ) . |
| | + | $$ |
| | | | |
| − | For the comultiplication restriction is used. Let <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r081/r081470/r081470159.png" /> be a representation of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r081/r081470/r081470160.png" />. For every <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r081/r081470/r081470161.png" />, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r081/r081470/r081470162.png" />, consider the restriction of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r081/r081470/r081470163.png" /> to <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r081/r081470/r081470164.png" /> to obtain an element of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r081/r081470/r081470165.png" />. The comultiplication of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r081/r081470/r081470166.png" /> is now defined by | + | For the comultiplication restriction is used. Let $ \rho $ |
| | + | be a representation of $ S _ {n} $. |
| | + | For every $ p, q \in \{ 0, 1 , \dots \} $, |
| | + | $ p+ q = n $, |
| | + | consider the restriction of $ \rho $ |
| | + | to $ S _ {p} \times S _ {q} $ |
| | + | to obtain an element of $ R ( S _ {p} \times S _ {q} ) = R ( S _ {p} ) \otimes R( S _ {q} ) $. |
| | + | The comultiplication of $ R $ |
| | + | is now defined by |
| | | | |
| − | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r081/r081470/r081470167.png" /></td> </tr></table>
| + | $$ |
| | + | \mu = \sum _ { p+ q= n} \mathrm{Res} _ {S _ {p} \times S _ {q} } ^ {S _ {n} } ( \rho ) . |
| | + | $$ |
| | | | |
| − | There is a unit mapping <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r081/r081470/r081470168.png" />, defined by identifying <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r081/r081470/r081470169.png" /> and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r081/r081470/r081470170.png" />, and an augmentation <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r081/r081470/r081470171.png" />, defined by <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r081/r081470/r081470172.png" /> identity on <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r081/r081470/r081470173.png" /> and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r081/r081470/r081470174.png" /> if <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r081/r081470/r081470175.png" />. It is a theorem that <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r081/r081470/r081470176.png" /> define a graded bi-algebra structure on <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r081/r081470/r081470177.png" />. There is also an antipode, making <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r081/r081470/r081470178.png" /> a graded Hopf algebra. | + | There is a unit mapping $ e : \mathbf Z \rightarrow R $, |
| | + | defined by identifying $ \mathbf Z $ |
| | + | and $ R( S _ {0} ) $, |
| | + | and an augmentation $ \epsilon : R \rightarrow \mathbf Z $, |
| | + | defined by $ \epsilon = $ |
| | + | identity on $ R( S _ {0} ) = \mathbf Z $ |
| | + | and $ \epsilon ( R( S _ {m} )) = 0 $ |
| | + | if $ m > 0 $. |
| | + | It is a theorem that $ ( m, \mu , e , \epsilon ) $ |
| | + | define a graded bi-algebra structure on $ R $. |
| | + | There is also an antipode, making $ R $ |
| | + | a graded Hopf algebra. |
| | | | |
| − | This Hopf algebra can be explicitly described as follows. Consider the commutative [[Ring of polynomials|ring of polynomials]] in infinitely many variables <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r081/r081470/r081470179.png" />, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r081/r081470/r081470180.png" />, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r081/r081470/r081470181.png" />, | + | This Hopf algebra can be explicitly described as follows. Consider the commutative [[Ring of polynomials|ring of polynomials]] in infinitely many variables $ c _ {i} $, |
| | + | $ i = 1, 2 , \dots $, |
| | + | $ c _ {0} = 1 $, |
| | | | |
| − | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r081/r081470/r081470182.png" /></td> </tr></table>
| + | $$ |
| | + | U = \mathbf Z [ c _ {1} , c _ {2} , \dots ] . |
| | + | $$ |
| | | | |
| | A [[Co-algebra|co-algebra]] structure is given by | | A [[Co-algebra|co-algebra]] structure is given by |
| | | | |
| − | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r081/r081470/r081470183.png" /></td> </tr></table>
| + | $$ |
| | + | c _ {n} \mapsto \sum _ { p+ q= n} c _ {p} \otimes c _ {q} , |
| | + | $$ |
| | | | |
| − | and a co-unit by <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r081/r081470/r081470184.png" />, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r081/r081470/r081470185.png" /> for <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r081/r081470/r081470186.png" />. There is also an antipode, making <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r081/r081470/r081470187.png" /> also a graded Hopf algebra. Perhaps the basic result in the representation theory of the symmetric groups is that <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r081/r081470/r081470188.png" /> and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r081/r081470/r081470189.png" /> are isomorphic as Hopf algebras. The isomorphism is very nearly unique because, [[#References|[a1]]], | + | and a co-unit by $ \epsilon ( c _ {0} ) = 1 $, |
| | + | $ \epsilon ( c _ {n} ) = 0 $ |
| | + | for $ n \geq 1 $. |
| | + | There is also an antipode, making $ U $ |
| | + | also a graded Hopf algebra. Perhaps the basic result in the representation theory of the symmetric groups is that $ R $ |
| | + | and $ U $ |
| | + | are isomorphic as Hopf algebras. The isomorphism is very nearly unique because, [[#References|[a1]]], |
| | | | |
| − | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r081/r081470/r081470190.png" /></td> </tr></table>
| + | $$ |
| | + | \mathrm{Aut} _ { {\rm Hopf} } ( U) = \ |
| | + | \mathbf Z /( 2) \times \mathbf Z / ( 2) . |
| | + | $$ |
| | | | |
| − | The individual components <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r081/r081470/r081470191.png" /> of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r081/r081470/r081470192.png" /> are also rings in themselves under the product of representations <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r081/r081470/r081470193.png" />, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r081/r081470/r081470194.png" />. This defines a second multiplication on <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r081/r081470/r081470195.png" />, which is distributive over the first, and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r081/r081470/r081470196.png" /> becomes a ring object in the category of co-algebras over <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r081/r081470/r081470197.png" />. Such objects have been called Hopf algebras, [[#References|[a6]]], and quite a few of them occur naturally in algebraic topology. The ring <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r081/r081470/r081470198.png" /> occurs in algebraic topology as <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r081/r081470/r081470199.png" />, the cohomology of the [[Classifying space|classifying space]] <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r081/r081470/r081470200.png" /> of complex <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r081/r081470/r081470201.png" />-theory, and there is a "natural direct isomorphism" <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r081/r081470/r081470202.png" />, [[#References|[a3]]]. (This explains the notation used above for <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r081/r081470/r081470203.png" />: the "ci" stand for Chern classes, cf. [[Chern class|Chern class]].) | + | The individual components $ R( S _ {m} ) $ |
| | + | of $ R $ |
| | + | are also rings in themselves under the product of representations $ \rho , \sigma \mapsto \rho \times \sigma $, |
| | + | $ ( \rho \times \sigma ) ( g) = \rho ( g) \otimes \sigma ( g) $. |
| | + | This defines a second multiplication on $ R $, |
| | + | which is distributive over the first, and $ R $ |
| | + | becomes a ring object in the category of co-algebras over $ \mathbf Z $. |
| | + | Such objects have been called Hopf algebras, [[#References|[a6]]], and quite a few of them occur naturally in algebraic topology. The ring $ U \simeq R $ |
| | + | occurs in algebraic topology as $ H ^ \star ( \mathbf{BU} ) $, |
| | + | the cohomology of the [[Classifying space|classifying space]] $ \mathbf{BU} $ |
| | + | of complex $ K $-theory, and there is a "natural direct isomorphism" $ R \simeq H ^ \star ( \mathbf{BU} ) $, |
| | + | [[#References|[a3]]]. (This explains the notation used above for $ U $: |
| | + | the "ci" stand for Chern classes, cf. [[Chern class|Chern class]].) |
| | | | |
| − | There is also an inner product on <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r081/r081470/r081470204.png" />: <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r081/r081470/r081470205.png" /> counts the number of irreducible representations that <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r081/r081470/r081470206.png" /> and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r081/r081470/r081470207.png" /> have in common, and with respect to this inner product <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r081/r081470/r081470208.png" /> is (graded) self-dual. In particular, the multiplication and comultiplication are adjoint to one another: | + | There is also an inner product on $ R = U $: |
| | + | $ \langle \rho , \sigma \rangle $ |
| | + | counts the number of irreducible representations that $ \rho $ |
| | + | and $ \sigma $ |
| | + | have in common, and with respect to this inner product $ R $ |
| | + | is (graded) self-dual. In particular, the multiplication and comultiplication are adjoint to one another: |
| | | | |
| − | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r081/r081470/r081470209.png" /></td> </tr></table>
| + | $$ |
| | + | \langle \rho , \sigma \tau \rangle = \ |
| | + | \langle \mu ( \rho ) , \sigma \otimes \tau \rangle , |
| | + | $$ |
| | | | |
| | which is the same as Frobenius reciprocity, cf. [[Induced representation|Induced representation]], in this case. | | which is the same as Frobenius reciprocity, cf. [[Induced representation|Induced representation]], in this case. |
| | | | |
| − | As a coring object in the category of algebras <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r081/r081470/r081470210.png" />, being the representing object <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r081/r081470/r081470211.png" /> of the functor of Witt vectors, [[#References|[a2]]], plays an important role in formal group theory. But, so far, no direct natural isomorphism has been found linking <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r081/r081470/r081470212.png" /> with <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r081/r081470/r081470213.png" /> in this manifestation. | + | As a coring object in the category of algebras $ U $, |
| | + | being the representing object $ R( W) $ |
| | + | of the functor of Witt vectors, [[#References|[a2]]], plays an important role in formal group theory. But, so far, no direct natural isomorphism has been found linking $ R $ |
| | + | with $ U = R( W) $ |
| | + | in this manifestation. |
| | | | |
| − | The ring <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r081/r081470/r081470214.png" /> also carries the structure of a [[Lambda-ring|<img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r081/r081470/r081470215.png" />-ring]] and it is in fact the universal <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r081/r081470/r081470217.png" />-ring on one generator, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r081/r081470/r081470218.png" />, [[#References|[a4]]], and this gives a natural isomorphism <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r081/r081470/r081470219.png" />, cf. [[Lambda-ring|<img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r081/r081470/r081470220.png" />-ring]] for some more details. | + | The ring $ U $ |
| | + | also carries the structure of a [[Lambda-ring| $ \lambda $-ring]] and it is in fact the universal $ \lambda $-ring on one generator, $ U( \Lambda ) $, |
| | + | [[#References|[a4]]], and this gives a natural isomorphism $ U( \Lambda ) \simeq R( W) $, |
| | + | cf. [[Lambda-ring| $ \lambda $-ring]] for some more details. |
| | | | |
| − | Finally there is a canonical notion of positivity on <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r081/r081470/r081470221.png" />: the actual (i.e. not virtual) representations are positive and the multiplication and comultiplication preserve positivity. This has led to the notion of a PSH-algebra, which stands for positive self-adjoint Hopf algebra, [[#References|[a5]]]. Essentially, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r081/r081470/r081470222.png" /> is the unique PSH-algebra on one generator and all other are tensor products of graded shifted copies of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r081/r081470/r081470223.png" />. This can be applied to other series of classical groups than the <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r081/r081470/r081470224.png" />, [[#References|[a5]]]. | + | Finally there is a canonical notion of positivity on $ \oplus R( S _ {n} ) $: |
| | + | the actual (i.e. not virtual) representations are positive and the multiplication and comultiplication preserve positivity. This has led to the notion of a PSH-algebra, which stands for positive self-adjoint Hopf algebra, [[#References|[a5]]]. Essentially, $ U $ |
| | + | is the unique PSH-algebra on one generator and all other are tensor products of graded shifted copies of $ U $. |
| | + | This can be applied to other series of classical groups than the $ S _ {m} $, |
| | + | [[#References|[a5]]]. |
| | | | |
| − | In combinatorics the algebra <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r081/r081470/r081470225.png" /> also has a long history. In modern terminology it is at the basis of the so-called umbral calculus, [[#References|[a7]]]. | + | In combinatorics the algebra $ U $ |
| | + | also has a long history. In modern terminology it is at the basis of the so-called umbral calculus, [[#References|[a7]]]. |
| | | | |
| | A modern reference to the representation theory of the symmetric groups, both ordinary and modular, is [[#References|[a8]]]. | | A modern reference to the representation theory of the symmetric groups, both ordinary and modular, is [[#References|[a8]]]. |
| | | | |
| | ====References==== | | ====References==== |
| − | <table><TR><TD valign="top">[a1]</TD> <TD valign="top"> A. Liulevicius, "Arrows, symmetries, and representation rings" ''J. Pure Appl. Algebra'' , '''19''' (1980) pp. 259–273</TD></TR><TR><TD valign="top">[a2]</TD> <TD valign="top"> M. Hazewinkel, "Formal rings and applications" , Acad. Press (1978)</TD></TR><TR><TD valign="top">[a3]</TD> <TD valign="top"> M.F. Atiyah, "Power operations in K-theory" ''Quarterly J. Math. (2)'' , '''17''' (1966) pp. 165–193</TD></TR><TR><TD valign="top">[a4]</TD> <TD valign="top"> D. Knutson, "<img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r081/r081470/r081470226.png" />-rings and the representation theory of the symmetric group" , Springer (1973)</TD></TR><TR><TD valign="top">[a5]</TD> <TD valign="top"> A.V. Zelevinsky, "Representations of finite classical groups" , Springer (1981)</TD></TR><TR><TD valign="top">[a6]</TD> <TD valign="top"> D.C. Ravenel, "The Hopf ring for complex cobordism" ''J. Pure Appl. Algebra'' , '''9''' (1977) pp. 241–280</TD></TR><TR><TD valign="top">[a7]</TD> <TD valign="top"> S. Roman, "The umbral calculus" , Acad. Press (1984)</TD></TR><TR><TD valign="top">[a8]</TD> <TD valign="top"> G. James, A. Kerber, "The representation theory of the symmetric group" , Addison-Wesley (1981)</TD></TR><TR><TD valign="top">[a9]</TD> <TD valign="top"> G. de B. Robinson, "Representation theory of the symmetric group" , Univ. Toronto Press (1961)</TD></TR><TR><TD valign="top">[a10]</TD> <TD valign="top"> J.A. Green, "Polynomial representations of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r081/r081470/r081470227.png" />" , ''Lect. notes in math.'' , '''830''' , Springer (1980)</TD></TR></table> | + | <table><TR><TD valign="top">[a1]</TD> <TD valign="top"> A. Liulevicius, "Arrows, symmetries, and representation rings" ''J. Pure Appl. Algebra'' , '''19''' (1980) pp. 259–273 {{MR|0593256}} {{ZBL|0448.55013}} </TD></TR><TR><TD valign="top">[a2]</TD> <TD valign="top"> M. Hazewinkel, "Formal rings and applications" , Acad. Press (1978)</TD></TR><TR><TD valign="top">[a3]</TD> <TD valign="top"> M.F. Atiyah, "Power operations in K-theory" ''Quarterly J. Math. (2)'' , '''17''' (1966) pp. 165–193 {{MR|0202130}} {{ZBL|0144.44901}} </TD></TR><TR><TD valign="top">[a4]</TD> <TD valign="top"> D. Knutson, "<img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r081/r081470/r081470226.png" />-rings and the representation theory of the symmetric group" , Springer (1973) {{MR|0364425}} {{ZBL|0272.20008}} </TD></TR><TR><TD valign="top">[a5]</TD> <TD valign="top"> A.V. Zelevinsky, "Representations of finite classical groups" , Springer (1981) {{MR|0643482}} {{ZBL|0465.20009}} </TD></TR><TR><TD valign="top">[a6]</TD> <TD valign="top"> D.C. Ravenel, "The Hopf ring for complex cobordism" ''J. Pure Appl. Algebra'' , '''9''' (1977) pp. 241–280 {{MR|0448337}} {{ZBL|0373.57020}} </TD></TR><TR><TD valign="top">[a7]</TD> <TD valign="top"> S. Roman, "The umbral calculus" , Acad. Press (1984) {{MR|0741185}} {{ZBL|0536.33001}} </TD></TR><TR><TD valign="top">[a8]</TD> <TD valign="top"> G. James, A. Kerber, "The representation theory of the symmetric group" , Addison-Wesley (1981) {{MR|0644144}} {{ZBL|0491.20010}} </TD></TR><TR><TD valign="top">[a9]</TD> <TD valign="top"> G. de B. Robinson, "Representation theory of the symmetric group" , Univ. Toronto Press (1961) {{MR|1531490}} {{MR|0125885}} {{ZBL|0102.02002}} </TD></TR><TR><TD valign="top">[a10]</TD> <TD valign="top"> J.A. Green, "Polynomial representations of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r081/r081470/r081470227.png" />" , ''Lect. notes in math.'' , '''830''' , Springer (1980) {{MR|0606556}} {{ZBL|0451.20037}} </TD></TR></table> |
A linear representation of the group $ S _ {m} $
over a field $ K $.
If $ \mathop{\rm char} K = 0 $,
then all finite-dimensional representations of the symmetric groups are completely reducible (cf. Reducible representation) and defined over $ \mathbf Q $ (in other words, irreducible finite-dimensional representations over $ \mathbf Q $
are absolutely irreducible).
The irreducible finite-dimensional representations of $ S _ {m} $
over $ \mathbf Q $
are classified as follows. Let $ d $
be a Young diagram corresponding to a partition $ \lambda = ( \lambda _ {1} \dots \lambda _ {r} ) $
of the number $ m $,
let $ R _ {d} $ (respectively, $ C _ {d} $)
be the subgroup of $ S _ {m} $
consisting of all permutations mapping each of the numbers $ 1 \dots m $
into a number in the same row (respectively, column) of $ d $.
Then
$$
R _ {d} \simeq \
S _ {\lambda _ {1} }
\times \dots \times
S _ {\lambda _ {r} }
$$
and
$$
C _ {d} \simeq \
S _ {\lambda _ {1} ^ \prime }
\times \dots \times
S _ {\lambda _ {s} ^ \prime } ,
$$
where $ \lambda ^ \prime = ( \lambda _ {1} ^ \prime \dots \lambda _ {s} ^ \prime ) $
is the partition of $ m $
dual to $ \lambda $.
There exists a unique irreducible representation $ T _ \lambda : S _ {m} \rightarrow \mathop{\rm GL} ( U _ \lambda ) $
of $ S _ {m} $ (depending on $ \lambda $
only) with the following properties: 1) in the space $ U _ \lambda $
there is a non-zero vector $ u _ {d} $
such that $ T _ \lambda ( g) u _ {d} = u _ {d} $
for any $ g \in R _ {d} $;
and 2) in $ U _ \lambda $
there exists a non-zero vector $ u _ {d} ^ \prime $
such that $ T _ \lambda ( g) u _ {d} ^ \prime = \epsilon ( g) u _ {d} ^ \prime $
for any $ g \in C _ {d} $,
where $ \epsilon ( g) = \pm 1 $
is the parity (sign) of $ g $.
Representations corresponding to distinct partitions are not equivalent, and they exhaust all irreducible representations of $ S _ {m} $
over $ Q $.
The vectors $ u _ {d} $
and $ u _ {d} ^ \prime $
are defined uniquely up to multiplication by a scalar. For all diagrams corresponding to a partition $ \lambda $
these vectors are normalized such that $ gu _ {d} = u _ {gd} $
and $ gu _ {d} ^ \prime = u _ {gd} ^ \prime $
for any $ g \in S _ {m} $.
Here $ gd $
denotes the diagram obtained from $ d $
by applying to all numbers the permutation $ g $.
The vectors $ u _ {d} $ (respectively, $ u _ {d} ^ \prime $)
corresponding to standard diagrams $ d $
form a basis for $ U _ \lambda $.
In this basis the operators of the representation $ T _ \lambda $
have the form of integral matrices. The dimension of $ T _ \lambda $
is
$$
\mathop{\rm dim} T _ \lambda = \
\frac{m! \prod _ {i < j }
( l _ {i} - l _ {j} ) }{\prod _ {i} l _ {i} ! }
= \
\frac{m! }{\prod _ {( i, j) } \lambda _ {ij} }
,
$$
where $ l _ {i} = \lambda _ {i} + r - i $,
$ i = 1 \dots r $,
and the product in the denominator of the last expression is taken over all cells $ c _ {ij} $
of the Young tableau $ t _ \lambda $;
$ \lambda _ {ij} $
denotes the length of the corresponding hook.
To the partition $ ( m) $
corresponds the trivial one-dimensional representation of $ S _ {m} $,
while to the partition $ ( 1, \dots, 1) $
corresponds the non-trivial one-dimensional representation $ \epsilon $ (the signature homomorphism, giving the parity or sign representation). To the partition $ \lambda ^ \prime $
dual to $ \lambda $
corresponds the representation $ \epsilon T _ \lambda $.
The space $ U _ {\lambda ^ \prime } $
can be identified (in a canonical way, up to a homothety) with $ U _ \lambda $,
so that $ T _ {\lambda ^ \prime } ( g) = \epsilon ( g) T _ \lambda ( g) $
for any $ g \in S _ {m} $.
Moreover, one may take $ u _ {d} ^ \prime = u _ {d ^ \prime } $,
where $ d ^ \prime $
is the diagram obtained from $ d $
by transposition.
The construction of a complete system of irreducible representations of a symmetric group invokes the use of the Young symmetrizer, and allows one to obtain the decomposition of the regular representation. If $ d $
is the Young diagram corresponding to a partition $ \lambda $,
then the representation $ T _ \lambda $
is equivalent to the representation of $ S _ {m} $
in the left ideal of the group algebra $ \mathbf Q S _ {m} $
generated by the Young symmetrizer $ e _ {d} $.
An a posteriori description of $ e _ {d} $
is the following: $ T _ \mu ( e _ {d} ) = 0 $
for $ \lambda \neq \mu $,
and $ T _ \lambda ( e _ {d} ) $
is the operator, of rank 1, acting by the formula $ T _ \lambda ( e _ {d} ) u = ( u _ {d} , u ) u _ {d} ^ \prime $
for any $ u \in U _ \lambda $.
Here $ ( , ) $
denotes the invariant scalar product in $ U _ \lambda $,
normalized in a suitable manner. Moreover,
$$
( u _ {d} , u _ {d} ^ \prime ) = \
\frac{m! }{ \mathop{\rm dim} U _ \lambda }
.
$$
The Frobenius formula gives a generating function for the characters of $ T _ \lambda $.
However, recurrence relations are more convenient to use when computing individual values of characters. The Murnagan–Nakayama rule is most effective: Let $ a _ {\lambda \mu } = a _ {\lambda \mu } ^ {(m)} $
be the value of a character of $ T _ \lambda $
on the class $ [ \mu ] $
of conjugate elements of $ S _ {m} $
defined by a partition $ \mu $
of $ m $,
and suppose that $ \mu $
contains a number $ p $.
Denote by $ \overline \mu $
the partition of $ m - p $
obtained from $ \mu $
by deleting $ p $.
Then
$$
a _ {\lambda \mu } ^ {(m)} = \
\sum _ {\overline \lambda }
(- 1) ^ {i ( \overline \lambda ) }
a _ {\overline \lambda \overline \mu } ^ {( m - p) } ,
$$
where the sum is over all partitions $ \overline \lambda $
of $ m - p $
obtained by deleting a skew hook of length $ p $
from the Young tableau $ t _ \lambda $,
and where $ i ( \overline \lambda ) $
denotes the height of the skew hook taken out.
There is also a method (cf. [5]) by which one can find the entire table of characters of $ S _ {m} $,
i.e. the matrix $ A = \| a _ {\lambda \mu } \| $.
Let $ M _ \lambda $
be the representation of $ S _ {m} $
induced by the trivial one-dimensional representation of the subgroup $ R _ \lambda = R _ {d} $,
where $ d $
is the Young diagram corresponding to the partition $ \lambda $.
Let $ M _ \lambda = \sum _ \mu m _ {\lambda \mu } T _ \mu $
and $ M = \| m _ {\lambda \mu } \| $.
If one assumes that the rows and columns of $ M $
are positioned in order of lexicographically decreasing indices (partitions), then $ M $
is a lower-triangular matrix with 1's on the diagonal. The value of a character of $ M _ \lambda $
on a class $ [ \mu ] $
is equal to
$$
b _ {\lambda \mu } = \
\frac{c _ \mu | R _ \lambda \cap [ \mu ] | }{| R _ \lambda | }
,
$$
where $ c _ \mu $
is the order of the centralizer of the permutations (a representative) from $ [ \mu ] $.
The matrix $ B = \| b _ {\lambda \mu } \| $
is upper triangular, and one has $ MM ^ {T} = BC ^ {-1} B ^ {T} $,
where $ C = \mathop{\rm diag} ( c _ \mu ) $,
from which $ M $
can be uniquely found. Then the matrix $ A $
is determined by
$$
A = M ^ {-1} B.
$$
The restriction of a representation $ T _ \lambda $
of $ S _ {m} $
to the subgroup $ S _ {m - 1 } $
can be found by the ramification rule
$$
T _ \lambda \mid _ {S _ {m - 1 } } = \
\sum _ { i } T _ {( \lambda _ {1} \dots \lambda _ {i} - 1 \dots \lambda _ {r} ) } ,
$$
where the summation extends over all $ i $
for which $ \lambda _ {i} > \lambda _ {i + 1 } $ (including $ r $).
The restriction of $ T _ \lambda $
to the subgroup $ A _ {m} $
is absolutely irreducible for $ \lambda \neq \lambda ^ \prime $
and splits for $ \lambda = \lambda ^ \prime $
over a quadratic extension of $ \mathbf Q $
into a sum of two non-equivalent absolutely-irreducible representations of equal dimension. The representations of $ A _ {m} $
thus obtained exhaust all its irreducible representations over $ \mathbf C $.
For representations of the symmetric groups in tensors see Representation of the classical groups.
The theory of modular representations of the symmetric groups has also been developed (see, e.g. [5]).
References
| [1] | H. Weyl, "The classical groups, their invariants and representations" , Princeton Univ. Press (1946) MR0000255 Zbl 1024.20502 |
| [2] | F.D. Murnagan, "The theory of group representations" , Johns Hopkins Univ. Press (1938) |
| [3] | M. Hamermesh, "Group theory and its application to physical problems" , Addison-Wesley (1962) MR0136667 Zbl 0100.36704 |
| [4] | C.W. Curtis, I. Reiner, "Representation theory of finite groups and associative algebras" , Interscience (1962) MR0144979 Zbl 0131.25601 |
| [5] | G.D. James, "The representation theory of the symmetric groups" , Springer (1978) MR0513828 Zbl 0393.20009 |
Let $ R ( S _ {m} ) $
be the free Abelian group generated by the complex irreducible representations of the symmetric group on $ m $
letters, $ S _ {m} $.
Now consider the direct sum
$$
R = \oplus _ { m= 0} ^ \infty R( S _ {m} ) ,\ \
R ( S _ {0} ) = \mathbf Z .
$$
It is possible to define a Hopf algebra structure on $ R $,
as follows. First the multiplication. Let $ \rho $
and $ \tau $
be, respectively, representations of $ S _ {n} $
and $ S _ {m} $.
Taking the tensor product defines a representation $ ( g, h) \mapsto \rho ( g) \otimes \sigma ( h) $
of $ S _ {n} \times S _ {m} $.
Consider $ S _ {n} \times S _ {m} $
as a subgroup of $ S _ {n+m} $
in the natural way. The product of $ \rho $
and $ \tau $
in $ R $
is now defined by taking the induced representation to $ S _ {n+m} $:
$$
\rho \sigma = \mathrm{Ind} _ {S _ {n} \times S _ {m} } ^ {S _ {n+m} } ( \rho \otimes \sigma ) .
$$
For the comultiplication restriction is used. Let $ \rho $
be a representation of $ S _ {n} $.
For every $ p, q \in \{ 0, 1 , \dots \} $,
$ p+ q = n $,
consider the restriction of $ \rho $
to $ S _ {p} \times S _ {q} $
to obtain an element of $ R ( S _ {p} \times S _ {q} ) = R ( S _ {p} ) \otimes R( S _ {q} ) $.
The comultiplication of $ R $
is now defined by
$$
\mu = \sum _ { p+ q= n} \mathrm{Res} _ {S _ {p} \times S _ {q} } ^ {S _ {n} } ( \rho ) .
$$
There is a unit mapping $ e : \mathbf Z \rightarrow R $,
defined by identifying $ \mathbf Z $
and $ R( S _ {0} ) $,
and an augmentation $ \epsilon : R \rightarrow \mathbf Z $,
defined by $ \epsilon = $
identity on $ R( S _ {0} ) = \mathbf Z $
and $ \epsilon ( R( S _ {m} )) = 0 $
if $ m > 0 $.
It is a theorem that $ ( m, \mu , e , \epsilon ) $
define a graded bi-algebra structure on $ R $.
There is also an antipode, making $ R $
a graded Hopf algebra.
This Hopf algebra can be explicitly described as follows. Consider the commutative ring of polynomials in infinitely many variables $ c _ {i} $,
$ i = 1, 2 , \dots $,
$ c _ {0} = 1 $,
$$
U = \mathbf Z [ c _ {1} , c _ {2} , \dots ] .
$$
A co-algebra structure is given by
$$
c _ {n} \mapsto \sum _ { p+ q= n} c _ {p} \otimes c _ {q} ,
$$
and a co-unit by $ \epsilon ( c _ {0} ) = 1 $,
$ \epsilon ( c _ {n} ) = 0 $
for $ n \geq 1 $.
There is also an antipode, making $ U $
also a graded Hopf algebra. Perhaps the basic result in the representation theory of the symmetric groups is that $ R $
and $ U $
are isomorphic as Hopf algebras. The isomorphism is very nearly unique because, [a1],
$$
\mathrm{Aut} _ { {\rm Hopf} } ( U) = \
\mathbf Z /( 2) \times \mathbf Z / ( 2) .
$$
The individual components $ R( S _ {m} ) $
of $ R $
are also rings in themselves under the product of representations $ \rho , \sigma \mapsto \rho \times \sigma $,
$ ( \rho \times \sigma ) ( g) = \rho ( g) \otimes \sigma ( g) $.
This defines a second multiplication on $ R $,
which is distributive over the first, and $ R $
becomes a ring object in the category of co-algebras over $ \mathbf Z $.
Such objects have been called Hopf algebras, [a6], and quite a few of them occur naturally in algebraic topology. The ring $ U \simeq R $
occurs in algebraic topology as $ H ^ \star ( \mathbf{BU} ) $,
the cohomology of the classifying space $ \mathbf{BU} $
of complex $ K $-theory, and there is a "natural direct isomorphism" $ R \simeq H ^ \star ( \mathbf{BU} ) $,
[a3]. (This explains the notation used above for $ U $:
the "ci" stand for Chern classes, cf. Chern class.)
There is also an inner product on $ R = U $:
$ \langle \rho , \sigma \rangle $
counts the number of irreducible representations that $ \rho $
and $ \sigma $
have in common, and with respect to this inner product $ R $
is (graded) self-dual. In particular, the multiplication and comultiplication are adjoint to one another:
$$
\langle \rho , \sigma \tau \rangle = \
\langle \mu ( \rho ) , \sigma \otimes \tau \rangle ,
$$
which is the same as Frobenius reciprocity, cf. Induced representation, in this case.
As a coring object in the category of algebras $ U $,
being the representing object $ R( W) $
of the functor of Witt vectors, [a2], plays an important role in formal group theory. But, so far, no direct natural isomorphism has been found linking $ R $
with $ U = R( W) $
in this manifestation.
The ring $ U $
also carries the structure of a $ \lambda $-ring and it is in fact the universal $ \lambda $-ring on one generator, $ U( \Lambda ) $,
[a4], and this gives a natural isomorphism $ U( \Lambda ) \simeq R( W) $,
cf. $ \lambda $-ring for some more details.
Finally there is a canonical notion of positivity on $ \oplus R( S _ {n} ) $:
the actual (i.e. not virtual) representations are positive and the multiplication and comultiplication preserve positivity. This has led to the notion of a PSH-algebra, which stands for positive self-adjoint Hopf algebra, [a5]. Essentially, $ U $
is the unique PSH-algebra on one generator and all other are tensor products of graded shifted copies of $ U $.
This can be applied to other series of classical groups than the $ S _ {m} $,
[a5].
In combinatorics the algebra $ U $
also has a long history. In modern terminology it is at the basis of the so-called umbral calculus, [a7].
A modern reference to the representation theory of the symmetric groups, both ordinary and modular, is [a8].
References
| [a1] | A. Liulevicius, "Arrows, symmetries, and representation rings" J. Pure Appl. Algebra , 19 (1980) pp. 259–273 MR0593256 Zbl 0448.55013 |
| [a2] | M. Hazewinkel, "Formal rings and applications" , Acad. Press (1978) |
| [a3] | M.F. Atiyah, "Power operations in K-theory" Quarterly J. Math. (2) , 17 (1966) pp. 165–193 MR0202130 Zbl 0144.44901 |
| [a4] | D. Knutson, "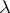 -rings and the representation theory of the symmetric group" , Springer (1973) MR0364425 Zbl 0272.20008 -rings and the representation theory of the symmetric group" , Springer (1973) MR0364425 Zbl 0272.20008 |
| [a5] | A.V. Zelevinsky, "Representations of finite classical groups" , Springer (1981) MR0643482 Zbl 0465.20009 |
| [a6] | D.C. Ravenel, "The Hopf ring for complex cobordism" J. Pure Appl. Algebra , 9 (1977) pp. 241–280 MR0448337 Zbl 0373.57020 |
| [a7] | S. Roman, "The umbral calculus" , Acad. Press (1984) MR0741185 Zbl 0536.33001 |
| [a8] | G. James, A. Kerber, "The representation theory of the symmetric group" , Addison-Wesley (1981) MR0644144 Zbl 0491.20010 |
| [a9] | G. de B. Robinson, "Representation theory of the symmetric group" , Univ. Toronto Press (1961) MR1531490 MR0125885 Zbl 0102.02002 |
| [a10] | J.A. Green, "Polynomial representations of 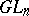 " , Lect. notes in math. , 830 , Springer (1980) MR0606556 Zbl 0451.20037 " , Lect. notes in math. , 830 , Springer (1980) MR0606556 Zbl 0451.20037 |
 -rings and the representation theory of the symmetric group" , Springer (1973) MR0364425 Zbl 0272.20008
-rings and the representation theory of the symmetric group" , Springer (1973) MR0364425 Zbl 0272.20008  " , Lect. notes in math. , 830 , Springer (1980) MR0606556 Zbl 0451.20037
" , Lect. notes in math. , 830 , Springer (1980) MR0606556 Zbl 0451.20037