Induced representation
A representation $ \pi $
of a locally compact group $ G $
induced by a representation $ \rho $
of a closed subgroup $ H $(
cf. Representation of a group). More precisely, it is a representation $ \pi $
of $ G $
in some space $ E $
of functions $ f $
on $ G $
taking values in the space $ V $
of the representation $ \rho $
and satisfying the condition $ f ( hg ) = \rho ( h) f ( g ) $
for all $ g \in G $,
$ h \in H $,
where $ [ \pi ( g _ {1} ) f ] ( g ) = f ( g g _ {1} ) $
for all $ f \in E $,
$ g , g _ {1} \in G $.
The induced representation $ \pi $
is usually denoted by $ \mathop{\rm Ind} \rho $,
$ \mathop{\rm Ind} _ {H} ^ {G} \rho $,
$ U ^ \rho $,
$ {} _ {H} U ^ \rho $,
or $ {} _ {H} U _ {G} ^ \rho $.
The operation of constructing an induced representation is the simplest and most important stage in the construction of representations of more complicated groups by starting from representations of simpler groups, and for a wide class of groups a complete description of the irreducible representations can be given in terms of induced representations or their generalizations.
If $ G $ is a finite group, then the inducing representation $ \rho $ is assumed to be finite-dimensional, while the space $ E $ is considered to be the space of all functions $ f $ on $ G $ taking values in $ V $ and satisfying the condition $ f ( hg ) = \rho ( h) f ( g) $. The representation $ {} _ {\{ e \} } U _ {G} ^ \rho $, where $ \rho $ is the identity representation of the identity subgroup $ \{ e \} $, is the right regular representation of $ G $; the representation $ {} _ {G} U _ {G} ^ \rho $ is equivalent to $ \rho $. The representation $ {} _ {H} U _ {G} ^ \rho $ is equivalent to the representation $ \sigma $ in the space $ W $ of all functions on the homogeneous space $ X = G / H $ with values in $ V $, defined by formulas of the form $ [ \sigma ( g) f ] ( x) = a ( g , x ) f ( xg ) $, where the function $ a $ is defined as follows: If $ s : X \rightarrow G $ is some mapping satisfying the condition $ s ( x) \in x $ for all $ x \in X $, then $ a ( g , x ) = \rho ( h ) $, where $ s ( x) g = hs ( xg ) $ for all $ x \in X $, $ g \in G $. The function $ a $ is a one-dimensional cocycle of the group $ G $ with coefficients in the group of functions on $ X $ with values in the invertible operators in $ V $. If $ \rho _ {1} $ is equivalent to a representation $ \rho _ {2} $, then $ \mathop{\rm Ind} \rho _ {1} $ is equivalent to $ \mathop{\rm Ind} \rho _ {2} $; the representation $ \mathop{\rm Ind} ( \rho \oplus \sigma ) $ is equivalent to $ \mathop{\rm Ind} \rho \oplus \mathop{\rm Ind} \sigma $. If $ K , H $ are subgroups of $ G $, $ K \subset H $ and if $ \rho $ is a representation of $ K $, then the representation of $ G $ induced by the representation $ {} _ {K} U _ {H} ^ \rho $ of $ H $ is equivalent to $ {} _ {K} U _ {G} ^ \rho $( the theorem on the composition of induced representations). If $ \pi , \rho $ are representations of the group $ G $ and the subgroup $ H $, respectively, then the spaces of intertwining operators (cf. Intertwining operator) $ \mathop{\rm Hom} ( \pi , {} _ {H} U _ {G} ^ \rho ) $ and $ \mathop{\rm Hom} ( \pi \mid _ {H} , \rho ) $ are isomorphic, where $ \pi \mid _ {H} $ is the restriction of $ \pi $ to $ H $( Frobenius' reciprocity theorem). In particular, if $ \pi $ and $ \rho $ are irreducible, then $ \pi $ occurs in $ U ^ \rho $ with the same multiplicity as that with which $ \rho $ occurs in $ \pi \mid _ {H} $. The character $ \chi _ \pi $ of the induced representation $ \pi = U ^ \rho $ of the group $ G $ is defined by the formula:
$$ \chi _ \pi ( g) = \ \sum _ {\{ \delta : {\delta y \in H \delta } \} } \chi _ \rho ( \delta g \delta ^ {-} 1 ) , $$
where $ \chi _ \rho $ is the character of the representation $ \rho $ of $ H $ extended by zero to the entire group $ G $ and $ \delta $ runs through the set of representatives of the right cosets of $ G $ by $ H $. Let $ H , K $ be subgroups of $ G $, let $ \rho $ be a representation of $ H $, let $ G _ {g} = K \cap g ^ {-} 1 H g $ for all $ g \in G $ and let $ \pi ^ {g} $ be the representation of $ K $ induced by the representation $ \rho ^ {g} $ of $ G _ {g} $ defined by the formula $ \rho ^ {g} ( x) = \rho ( g x g ^ {-} 1 ) $, $ x \in G _ {g} $. Then $ \pi ^ {g} $ is uniquely determined by the double coset $ H g K $ containing the element $ g $, and the restriction of the induced representation $ {} _ {H} U _ {G} ^ \rho $ to $ K $ is equivalent to the direct sum of the representations $ \pi ^ {g} $, where the sum is taken over a set of representatives of all possible double cosets $ H g K $, $ g \in G $( the theorem on the restriction of an induced representation to a subgroup). This theorem can be applied, in particular, to the decomposition of a tensor product of induced representations. The space of operators intertwining a given induced representation admits an explicit description. A representation $ \pi $ of a group $ G $ is equivalent to an induced representation of the type $ {} _ {H} U _ {G} ^ \rho $ for some $ H $ and $ \rho $ if and only if there exists a mapping from the set of subsets of $ H \setminus G $ to the set of projections in the space $ E $ of the representation $ \pi $, such that 1) $ P (\emptyset) = 0 $, $ P ( H \setminus G ) = 1 $; 2) if $ M , N \subset H \setminus G $ and $ M \cap N = \emptyset $, then $ P ( M \cup N ) = P ( M) + P ( N) $; 3) $ P ( M \cap N ) = P ( M) P ( N) $ for all $ M , N \subset H \setminus G $; and 4) $ P ( M g ) = \pi ^ {-} 1 ( g) P ( M) \pi ( g) $ for all $ M \subset H \setminus G $, $ g \in G $( such a mapping $ P $ is called a system of imprimitivity for the representation $ \pi $ with basis $ H \setminus G $). An induced representation of a finite group can be described directly in terms of moduli over group algebras and can also be defined in categorical terms. A finite group is called monomial if each of its irreducible representations is induced by a one-dimensional representation of some subgroup. Every monomial group is solvable (cf. Solvable group); every nilpotent group is monomial.
The definition of an induced representation of a locally compact group $ G $ depends essentially on the choice of the space $ E $; for example, one often takes $ E $ to be the space of all continuous functions on $ G $ satisfying the condition $ f ( h g ) = \rho ( h) f ( g) $, or (if $ G $ is a Lie group) the space of all differentiable functions on $ G $ satisfying the same condition. On the other hand, let $ \rho $ be a continuous unitary representation of a closed subgroup $ H \subset G $ in a Hilbert space $ V $ and let $ s $ be a measurable mapping of the locally compact space $ X = H \setminus G $ into $ G $ satisfying the condition $ s ( x) \in x $ for $ x \in X $; let $ \Delta _ {G} $ and $ \Delta _ {H} $ be the moduli of the groups $ G $ and $ H $, respectively (see Haar measure), and let $ \nu _ {s} $ be a $ G $- quasi-invariant measure on $ X $ such that
$$ \frac{d \nu _ {s} ( x g ) }{d \nu _ {s} ( x) } = \ \Delta _ {H} ( h ^ {x,g} ) \Delta _ {G} ^ {-} 1 ( h ^ {x,g} ) , $$
where $ s ( x) g = h ^ {x,g} s ( x g ) $ for all $ x \in X $, $ g \in G $; let $ L _ {2} ( G , H , \rho ) $ be the Hilbert space of measurable vector functions $ F $ on $ G $ with values in $ V $ satisfying the condition
$$ F ( h g ) = \ \left [ \frac{\Delta _ {H} ( h) }{\Delta _ {G} ( h) } \right ] ^ {1/2} \cdot \rho ( h) F ( g) $$
for all $ h \in H $, $ g \in G $, and such that the integral
$$ \int\limits _ { X } \| F ( s ( x) ) \| _ {V} ^ {2} d \nu _ {s} ( x) $$
converges; then the continuous unitary representation $ \pi $ of $ G $ in $ L _ {2} ( G , H , \rho ) $ defined by the formula
$$ [ \pi ( g _ {1} ) F ] ( g) = F ( g g _ {1} ) $$
for all $ g , g _ {1} \in G $, $ F \in L _ {2} ( G , H , \rho ) $, is called the unitary induced representation of the locally compact group $ G $. The majority of results on induced representations of finite groups admit a generalization to the case of unitary induced representations of locally compact groups. Among them are the properties of the representations $ \mathop{\rm Ind} ( \rho _ {1} \oplus \rho _ {2} ) $ and $ \mathop{\rm Ind} ( \rho _ {1} \otimes \rho _ {2} ) $, the connection between induced representations and cocycles on $ G $, the theorem on composition of induced representations, the theorem on the restriction of an induced representation to a subgroup, the formula for the character of an induced representation, the inducibility criterion of a representation, properties of monomial groups, and the Frobenius reciprocity theorem. These admit more or less direct generalizations to the case of unitary induced representations. Induced representations of a locally compact group $ G $ are related to representations of certain generalized group algebras of this group. If $ G $ is a Lie group, then the notion of an induced representation of $ G $ admits various generalizations, including that of a holomorphically-induced representation, whose representation space $ E $ is the space of functions on $ G $ that are analytic in some of the variables, and the notion of a representation in vector bundle cohomology over the homogeneous space of $ G $( representations in zero cohomology are the induced representations). The notion of an induced representation and its generalizations play a fruitful role in representation theory. In particular, the representations of group extensions can be described in terms of unitary induced representations; the fundamental series of continuous unitary representations of a connected real semi-simple Lie group $ G $ is formed by induced representations, namely, the induced finite-dimensional unitary representations of the Borel subgroup of $ G $; the discrete series of representations of a linear real semi-simple Lie group is realized in certain vector bundle cohomology over the homogeneous spaces of this group; irreducible continuous unitary representations of solvable connected Lie groups of type $ I $ can be described in terms of holomorphically-induced representations [7]. The operation of forming an induced representation can be generalized to the case of non-unitary representations of locally compact groups, as well as to topological groups that are not locally compact. The analogue of induced representations for $ C ^ {*} $- algebras has been studied [6].
References
| [1] | A.A. Kirillov, "Elements of the theory of representations" , Springer (1976) (Translated from Russian) |
| [2] | M.A. Naimark, "Theory of group representations" , Springer (1982) (Translated from Russian) |
| [3] | J.-P. Serre, "Linear representations of finite groups" , Springer (1977) (Translated from French) |
| [4] | G.W. Mackey, "Infinite-dimensional group representations" Bull. Amer. Math. Soc. , 69 (1963) pp. 628–686 |
| [5] | W. Schmid, "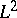 cohomology and the discrete series" Ann. of Math. , 103 (1976) pp. 375–394 cohomology and the discrete series" Ann. of Math. , 103 (1976) pp. 375–394 |
| [6] | M. Rieffel, "Induced representations of 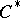 -algebras" Adv. in Math. , 13 : 2 (1974) pp. 176–257 -algebras" Adv. in Math. , 13 : 2 (1974) pp. 176–257 |
| [7] | L. Auslander, B. Konstant, "Polarization and unitary representations of solvable Lie groups" Invent. Math. , 14 : 4 (1971) pp. 255–354 |
| [8] | A.M. Vershik, I.M. Gel'fand, M.I. Graev, "Representations of the group of diffeomorphisms" Russian Math. Surveys , 30 : 6 (1975) pp. 1–50 Uspekhi Mat. Nauk , 30 : 6 (1975) pp. 3–50 |
| [9] | M.B. Menskii, "The method of induced representations. Space-time and the concept of a particle" , Moscow (1976) (In Russian) |
Comments
The "theorem on composition of induced representations" is also called the theorem on induction by stages.
Induced representation. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Induced_representation&oldid=47334