Difference between revisions of "Fundamental forms of a surface"
(Importing text file) |
Ulf Rehmann (talk | contribs) m (tex encoded by computer) |
||
| Line 1: | Line 1: | ||
| + | <!-- | ||
| + | f0422001.png | ||
| + | $#A+1 = 37 n = 0 | ||
| + | $#C+1 = 37 : ~/encyclopedia/old_files/data/F042/F.0402200 Fundamental forms of a surface | ||
| + | Automatically converted into TeX, above some diagnostics. | ||
| + | Please remove this comment and the {{TEX|auto}} line below, | ||
| + | if TeX found to be correct. | ||
| + | --> | ||
| + | |||
| + | {{TEX|auto}} | ||
| + | {{TEX|done}} | ||
| + | |||
The general name for the quadratic differential forms of the surface given in coordinates on the surface and satisfying the usual transformation laws under transformations of these coordinates. The fundamental forms of a surface characterize the basic intrinsic properties of the surface and the way it is located in space in a neighbourhood of a given point; one usually singles out the so-called first, second and third fundamental forms. | The general name for the quadratic differential forms of the surface given in coordinates on the surface and satisfying the usual transformation laws under transformations of these coordinates. The fundamental forms of a surface characterize the basic intrinsic properties of the surface and the way it is located in space in a neighbourhood of a given point; one usually singles out the so-called first, second and third fundamental forms. | ||
The first fundamental form characterizes the [[Interior geometry|interior geometry]] of the surface in a neighbourhood of a given point. This means that measurements on the surface can be carried out by means of it. Suppose that the surface is given by the equation | The first fundamental form characterizes the [[Interior geometry|interior geometry]] of the surface in a neighbourhood of a given point. This means that measurements on the surface can be carried out by means of it. Suppose that the surface is given by the equation | ||
| − | + | $$ | |
| + | \mathbf r = \mathbf r ( u , v ) , | ||
| + | $$ | ||
| − | where | + | where $ u $ |
| + | and $ v $ | ||
| + | are coordinates on the surface; and | ||
| − | + | $$ | |
| + | d \mathbf r = \mathbf r _ {u} d u + \mathbf r _ {v} d v | ||
| + | $$ | ||
| − | is the differential of the radius vector | + | is the differential of the radius vector $ \mathbf r ( u , v ) $ |
| + | along a chosen direction from a point $ M $ | ||
| + | to an infinitesimally close point $ M ^ { \prime } $( | ||
| + | see Fig. a). | ||
<img style="border:1px solid;" src="https://www.encyclopediaofmath.org/legacyimages/common_img/f042200a.gif" /> | <img style="border:1px solid;" src="https://www.encyclopediaofmath.org/legacyimages/common_img/f042200a.gif" /> | ||
| Line 15: | Line 36: | ||
Figure: f042200a | Figure: f042200a | ||
| − | The principal linear part of growth of the arc length | + | The principal linear part of growth of the arc length $ M M ^ { \prime } $ |
| + | is expressed by the square of $ d \mathbf r $: | ||
| − | + | $$ | |
| + | \textrm{ I } = d s ^ {2} = d | ||
| + | \mathbf r ^ {2} = E ( u , v ) d u ^ {2} + 2 F ( u , v ) \ | ||
| + | d u d v + G ( u , v ) d v ^ {2} , | ||
| + | $$ | ||
where | where | ||
| − | + | $$ | |
| + | E ( u , v ) = \mathbf r _ {u} ^ {2} ,\ F ( u , v ) = \ | ||
| + | ( \mathbf r _ {u} , \mathbf r _ {v} ) ,\ \ | ||
| + | G ( u , v ) = \mathbf r _ {v} ^ {2} . | ||
| + | $$ | ||
| − | The form | + | The form $ \textrm{ I } $ |
| + | is the first fundamental form of the surface. See also [[First fundamental form|first fundamental form]] of a surface. | ||
The second fundamental form characterizes the local structure of the surface in a neighbourhood of a regular point. Thus, choose | The second fundamental form characterizes the local structure of the surface in a neighbourhood of a regular point. Thus, choose | ||
| − | + | $$ | |
| + | \mathbf n = \ | ||
| + | |||
| + | \frac{\epsilon [ \mathbf r _ {u} , \mathbf r _ {v} ] }{| [ \mathbf r _ {u} , \mathbf r _ {v} ] | } | ||
| + | , | ||
| + | $$ | ||
| − | a unit normal vector to the surface at | + | a unit normal vector to the surface at $ M $, |
| + | where $ \epsilon = + 1 $ | ||
| + | if the triple of vectors $ \{ \mathbf r _ {u} , \mathbf r _ {v} , \mathbf n \} $ | ||
| + | has a right-hand orientation and $ \epsilon = - 1 $ | ||
| + | in the opposite case. The doubled principal linear part $ 2 \delta $ | ||
| + | of the deviation of the point $ M ^ { \prime } $ | ||
| + | on the surface (see Fig. b) from the tangent plane at the point $ M $ | ||
| + | is given by | ||
| − | + | $$ | |
| + | \textrm{ II } = 2 \delta = ( - d \mathbf r , d \mathbf n ) = | ||
| + | $$ | ||
| − | + | $$ | |
| + | = \ | ||
| + | L ( u , v ) d u ^ {2} + 2 M ( u , v ) d u d v + N ( u , v ) d v ^ {2} , | ||
| + | $$ | ||
where | where | ||
| − | + | $$ | |
| + | L = ( \mathbf r _ {uu} , \mathbf n ) ,\ \ | ||
| + | M = ( \mathbf r _ {uv} , \mathbf n ) ,\ \ | ||
| + | N = ( \mathbf r _ {vv} , \mathbf n ) . | ||
| + | $$ | ||
<img style="border:1px solid;" src="https://www.encyclopediaofmath.org/legacyimages/common_img/f042200b.gif" /> | <img style="border:1px solid;" src="https://www.encyclopediaofmath.org/legacyimages/common_img/f042200b.gif" /> | ||
| Line 43: | Line 95: | ||
Figure: f042200b | Figure: f042200b | ||
| − | The form | + | The form $ \textrm{ II } $ |
| + | is called the second fundamental form of the surface. See also [[Second fundamental form|Second fundamental form]]. | ||
The first and second fundamental forms define two important common scalar quantities which are invariant under a transformation of the coordinates on the surface. Namely, the determinant of the ratio of the second with respect to the first one is the [[Gaussian curvature|Gaussian curvature]] of the surface at the point: | The first and second fundamental forms define two important common scalar quantities which are invariant under a transformation of the coordinates on the surface. Namely, the determinant of the ratio of the second with respect to the first one is the [[Gaussian curvature|Gaussian curvature]] of the surface at the point: | ||
| − | + | $$ | |
| + | K = \ | ||
| + | |||
| + | \frac{L N - M ^ {2} }{E G - F ^ {2} } | ||
| + | , | ||
| + | $$ | ||
while the trace of this ratio, | while the trace of this ratio, | ||
| − | + | $$ | |
| + | H = | ||
| + | \frac{1}{2} | ||
| + | |||
| + | \frac{E N - 2 F M + G L }{E G - F ^ {2} } | ||
| + | , | ||
| + | $$ | ||
defines the [[Mean curvature|mean curvature]] of the surface at the point. | defines the [[Mean curvature|mean curvature]] of the surface at the point. | ||
| Line 57: | Line 121: | ||
Specifying the first (positive definite) and second fundamental forms defines the surface up to a motion (the [[Bonnet theorem|Bonnet theorem]]). | Specifying the first (positive definite) and second fundamental forms defines the surface up to a motion (the [[Bonnet theorem|Bonnet theorem]]). | ||
| − | The third fundamental form of the surface is the square of the differential of the unit normal vector | + | The third fundamental form of the surface is the square of the differential of the unit normal vector $ \mathbf n $ |
| + | to the surface at the point $ M $( | ||
| + | see Fig. c): | ||
| − | + | $$ | |
| + | \textrm{ III } = d \mathbf n ^ {2} = \ | ||
| + | \mathbf n _ {u} ^ {2} d u ^ {2} + | ||
| + | 2 \mathbf n _ {u} \mathbf n _ {v} \ | ||
| + | d u dv + \mathbf n _ {v} ^ {2} d v ^ {2} . | ||
| + | $$ | ||
<img style="border:1px solid;" src="https://www.encyclopediaofmath.org/legacyimages/common_img/f042200c.gif" /> | <img style="border:1px solid;" src="https://www.encyclopediaofmath.org/legacyimages/common_img/f042200c.gif" /> | ||
| Line 65: | Line 136: | ||
Figure: f042200c | Figure: f042200c | ||
| − | The third fundamental form of a surface is equal to the principal linear part of growth of the angle between the vectors | + | The third fundamental form of a surface is equal to the principal linear part of growth of the angle between the vectors $ \mathbf n $ |
| + | and $ \mathbf n ^ \prime $ | ||
| + | under displacement along the surface from $ M $ | ||
| + | to $ M ^ { \prime } $; | ||
| + | it is the first fundamental form of the spherical image of the surface (cf. [[Spherical map|Spherical map]]). | ||
The three fundamental forms are related by the linear dependence | The three fundamental forms are related by the linear dependence | ||
| − | + | $$ | |
| + | \textrm{ I } \cdot K - \textrm{ II } \cdot 2 H + \textrm{ III } = 0 . | ||
| + | $$ | ||
In addition to the fundamental forms listed above, other fundamental forms are sometimes encountered (see, for example, [[#References|[3]]]). | In addition to the fundamental forms listed above, other fundamental forms are sometimes encountered (see, for example, [[#References|[3]]]). | ||
| Line 75: | Line 152: | ||
====References==== | ====References==== | ||
<table><TR><TD valign="top">[1]</TD> <TD valign="top"> V.F. Kagan, "Foundations of the theory of surfaces in a tensor setting" , '''1''' , Moscow-Leningrad (1947) (In Russian)</TD></TR><TR><TD valign="top">[2]</TD> <TD valign="top"> P.K. Rashevskii, "A course of differential geometry" , Moscow (1956) (In Russian)</TD></TR><TR><TD valign="top">[3]</TD> <TD valign="top"> V.I. Shulikovskii, "Classical differential geometry in a tensor setting" , Moscow (1963) (In Russian)</TD></TR></table> | <table><TR><TD valign="top">[1]</TD> <TD valign="top"> V.F. Kagan, "Foundations of the theory of surfaces in a tensor setting" , '''1''' , Moscow-Leningrad (1947) (In Russian)</TD></TR><TR><TD valign="top">[2]</TD> <TD valign="top"> P.K. Rashevskii, "A course of differential geometry" , Moscow (1956) (In Russian)</TD></TR><TR><TD valign="top">[3]</TD> <TD valign="top"> V.I. Shulikovskii, "Classical differential geometry in a tensor setting" , Moscow (1963) (In Russian)</TD></TR></table> | ||
| − | |||
| − | |||
====Comments==== | ====Comments==== | ||
| − | See also [[Quadratic surface forms|Quadratic surface forms]]; | + | See also [[Quadratic surface forms|Quadratic surface forms]]; $ [ \mathbf r _ {u} , \mathbf r _ {v} ] $ |
| + | denotes the [[Vector product|vector product]] of the vectors $ \mathbf r _ {u} $ | ||
| + | and $ \mathbf r _ {v} $. | ||
====References==== | ====References==== | ||
<table><TR><TD valign="top">[a1]</TD> <TD valign="top"> W. Klingenberg, "A course in differential geometry" , Springer (1978) (Translated from German)</TD></TR><TR><TD valign="top">[a2]</TD> <TD valign="top"> M. Spivak, "A comprehensive introduction to differential geometry" , '''1979''' , Publish or Perish pp. 1–5</TD></TR><TR><TD valign="top">[a3]</TD> <TD valign="top"> W. Blaschke, K. Leichtweiss, "Elementare Differentialgeometrie" , Springer (1975)</TD></TR><TR><TD valign="top">[a4]</TD> <TD valign="top"> N.J. Hicks, "Notes on differential geometry" , v. Nostrand (1965)</TD></TR></table> | <table><TR><TD valign="top">[a1]</TD> <TD valign="top"> W. Klingenberg, "A course in differential geometry" , Springer (1978) (Translated from German)</TD></TR><TR><TD valign="top">[a2]</TD> <TD valign="top"> M. Spivak, "A comprehensive introduction to differential geometry" , '''1979''' , Publish or Perish pp. 1–5</TD></TR><TR><TD valign="top">[a3]</TD> <TD valign="top"> W. Blaschke, K. Leichtweiss, "Elementare Differentialgeometrie" , Springer (1975)</TD></TR><TR><TD valign="top">[a4]</TD> <TD valign="top"> N.J. Hicks, "Notes on differential geometry" , v. Nostrand (1965)</TD></TR></table> | ||
Latest revision as of 19:40, 5 June 2020
The general name for the quadratic differential forms of the surface given in coordinates on the surface and satisfying the usual transformation laws under transformations of these coordinates. The fundamental forms of a surface characterize the basic intrinsic properties of the surface and the way it is located in space in a neighbourhood of a given point; one usually singles out the so-called first, second and third fundamental forms.
The first fundamental form characterizes the interior geometry of the surface in a neighbourhood of a given point. This means that measurements on the surface can be carried out by means of it. Suppose that the surface is given by the equation
$$ \mathbf r = \mathbf r ( u , v ) , $$
where $ u $ and $ v $ are coordinates on the surface; and
$$ d \mathbf r = \mathbf r _ {u} d u + \mathbf r _ {v} d v $$
is the differential of the radius vector $ \mathbf r ( u , v ) $ along a chosen direction from a point $ M $ to an infinitesimally close point $ M ^ { \prime } $( see Fig. a).
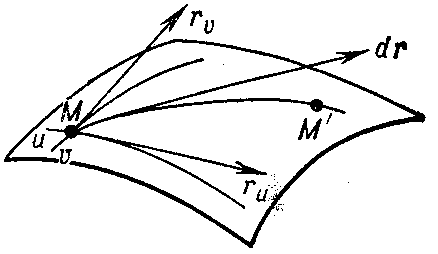
Figure: f042200a
The principal linear part of growth of the arc length $ M M ^ { \prime } $ is expressed by the square of $ d \mathbf r $:
$$ \textrm{ I } = d s ^ {2} = d \mathbf r ^ {2} = E ( u , v ) d u ^ {2} + 2 F ( u , v ) \ d u d v + G ( u , v ) d v ^ {2} , $$
where
$$ E ( u , v ) = \mathbf r _ {u} ^ {2} ,\ F ( u , v ) = \ ( \mathbf r _ {u} , \mathbf r _ {v} ) ,\ \ G ( u , v ) = \mathbf r _ {v} ^ {2} . $$
The form $ \textrm{ I } $ is the first fundamental form of the surface. See also first fundamental form of a surface.
The second fundamental form characterizes the local structure of the surface in a neighbourhood of a regular point. Thus, choose
$$ \mathbf n = \ \frac{\epsilon [ \mathbf r _ {u} , \mathbf r _ {v} ] }{| [ \mathbf r _ {u} , \mathbf r _ {v} ] | } , $$
a unit normal vector to the surface at $ M $, where $ \epsilon = + 1 $ if the triple of vectors $ \{ \mathbf r _ {u} , \mathbf r _ {v} , \mathbf n \} $ has a right-hand orientation and $ \epsilon = - 1 $ in the opposite case. The doubled principal linear part $ 2 \delta $ of the deviation of the point $ M ^ { \prime } $ on the surface (see Fig. b) from the tangent plane at the point $ M $ is given by
$$ \textrm{ II } = 2 \delta = ( - d \mathbf r , d \mathbf n ) = $$
$$ = \ L ( u , v ) d u ^ {2} + 2 M ( u , v ) d u d v + N ( u , v ) d v ^ {2} , $$
where
$$ L = ( \mathbf r _ {uu} , \mathbf n ) ,\ \ M = ( \mathbf r _ {uv} , \mathbf n ) ,\ \ N = ( \mathbf r _ {vv} , \mathbf n ) . $$
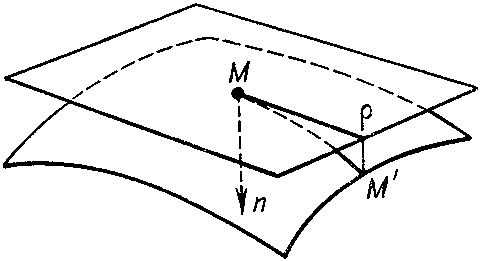
Figure: f042200b
The form $ \textrm{ II } $ is called the second fundamental form of the surface. See also Second fundamental form.
The first and second fundamental forms define two important common scalar quantities which are invariant under a transformation of the coordinates on the surface. Namely, the determinant of the ratio of the second with respect to the first one is the Gaussian curvature of the surface at the point:
$$ K = \ \frac{L N - M ^ {2} }{E G - F ^ {2} } , $$
while the trace of this ratio,
$$ H = \frac{1}{2} \frac{E N - 2 F M + G L }{E G - F ^ {2} } , $$
defines the mean curvature of the surface at the point.
Specifying the first (positive definite) and second fundamental forms defines the surface up to a motion (the Bonnet theorem).
The third fundamental form of the surface is the square of the differential of the unit normal vector $ \mathbf n $ to the surface at the point $ M $( see Fig. c):
$$ \textrm{ III } = d \mathbf n ^ {2} = \ \mathbf n _ {u} ^ {2} d u ^ {2} + 2 \mathbf n _ {u} \mathbf n _ {v} \ d u dv + \mathbf n _ {v} ^ {2} d v ^ {2} . $$
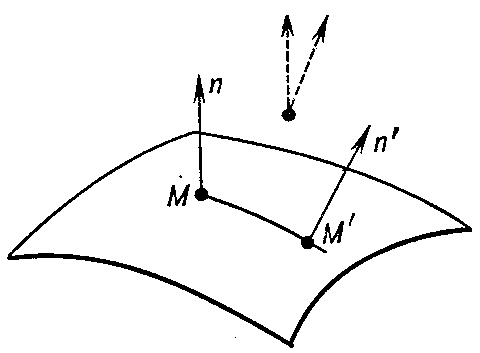
Figure: f042200c
The third fundamental form of a surface is equal to the principal linear part of growth of the angle between the vectors $ \mathbf n $ and $ \mathbf n ^ \prime $ under displacement along the surface from $ M $ to $ M ^ { \prime } $; it is the first fundamental form of the spherical image of the surface (cf. Spherical map).
The three fundamental forms are related by the linear dependence
$$ \textrm{ I } \cdot K - \textrm{ II } \cdot 2 H + \textrm{ III } = 0 . $$
In addition to the fundamental forms listed above, other fundamental forms are sometimes encountered (see, for example, [3]).
References
| [1] | V.F. Kagan, "Foundations of the theory of surfaces in a tensor setting" , 1 , Moscow-Leningrad (1947) (In Russian) |
| [2] | P.K. Rashevskii, "A course of differential geometry" , Moscow (1956) (In Russian) |
| [3] | V.I. Shulikovskii, "Classical differential geometry in a tensor setting" , Moscow (1963) (In Russian) |
Comments
See also Quadratic surface forms; $ [ \mathbf r _ {u} , \mathbf r _ {v} ] $ denotes the vector product of the vectors $ \mathbf r _ {u} $ and $ \mathbf r _ {v} $.
References
| [a1] | W. Klingenberg, "A course in differential geometry" , Springer (1978) (Translated from German) |
| [a2] | M. Spivak, "A comprehensive introduction to differential geometry" , 1979 , Publish or Perish pp. 1–5 |
| [a3] | W. Blaschke, K. Leichtweiss, "Elementare Differentialgeometrie" , Springer (1975) |
| [a4] | N.J. Hicks, "Notes on differential geometry" , v. Nostrand (1965) |
Fundamental forms of a surface. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Fundamental_forms_of_a_surface&oldid=13236