|
|
| (2 intermediate revisions by one other user not shown) |
| Line 1: |
Line 1: |
| − | A [[Hilbert space|Hilbert space]] <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/h/h047/h047390/h0473901.png" /> over the field of complex numbers endowed with a continuous bilinear (more exactly, sesquilinear) form <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/h/h047/h047390/h0473902.png" /> that is not, generally speaking, positive definite. The form <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/h/h047/h047390/h0473903.png" /> is often referred to as the <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/h/h047/h047390/h0473905.png" />-metric. The most important example of a Hilbert space with an indefinite metric is a so-called <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/h/h047/h047390/h0473907.png" />-space — a Hilbert space with an indefinite metric in which <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/h/h047/h047390/h0473908.png" /> is defined by a certain Hermitian involution <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/h/h047/h047390/h0473909.png" /> in <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/h/h047/h047390/h04739010.png" /> by the formula <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/h/h047/h047390/h04739011.png" />. The form <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/h/h047/h047390/h04739012.png" /> is then also denoted by the letter <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/h/h047/h047390/h04739013.png" /> and is called a <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/h/h047/h047390/h04739015.png" />-metric. The involution <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/h/h047/h047390/h04739016.png" /> may be represented as <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/h/h047/h047390/h04739017.png" />, where <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/h/h047/h047390/h04739018.png" /> and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/h/h047/h047390/h04739019.png" /> are orthogonal projections in <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/h/h047/h047390/h04739020.png" />, and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/h/h047/h047390/h04739021.png" />; the number <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/h/h047/h047390/h04739022.png" /> is called the rank of indefiniteness of the <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/h/h047/h047390/h04739025.png" />-metric or of the <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/h/h047/h047390/h04739026.png" />-space. If <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/h/h047/h047390/h04739027.png" />, the Hilbert space with the indefinite metric <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/h/h047/h047390/h04739028.png" /> is called a [[Pontryagin space|Pontryagin space]] <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/h/h047/h047390/h04739029.png" />; see also [[Space with an indefinite metric|Space with an indefinite metric]].
| + | <!-- |
| | + | h0473901.png |
| | + | $#A+1 = 203 n = 1 |
| | + | $#C+1 = 203 : ~/encyclopedia/old_files/data/H047/H.0407390 Hilbert space with an indefinite metric |
| | + | Automatically converted into TeX, above some diagnostics. |
| | + | Please remove this comment and the {{TEX|auto}} line below, |
| | + | if TeX found to be correct. |
| | + | --> |
| | | | |
| − | Two Hilbert spaces <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/h/h047/h047390/h04739030.png" /> and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/h/h047/h047390/h04739031.png" /> with indefinite metrics are said to be metrically equivalent if there exists a linear homeomorphism <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/h/h047/h047390/h04739032.png" /> of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/h/h047/h047390/h04739033.png" /> onto <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/h/h047/h047390/h04739034.png" /> which transforms <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/h/h047/h047390/h04739035.png" /> to <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/h/h047/h047390/h04739036.png" />. A <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/h/h047/h047390/h04739037.png" />-metric generated by an invertible Hermitian operator <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/h/h047/h047390/h04739038.png" /> by the formula <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/h/h047/h047390/h04739039.png" /> is said to be regular; after the introduction of a new scalar product that is metrically equivalent to the old one a regular <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/h/h047/h047390/h04739041.png" />-metric becomes a <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/h/h047/h047390/h04739042.png" />-metric. Any Hilbert space with an indefinite metric with a Hermitian form <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/h/h047/h047390/h04739043.png" /> may be <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/h/h047/h047390/h04739044.png" />-isometrically (i.e. with preservation of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/h/h047/h047390/h04739045.png" />) imbedded in some <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/h/h047/h047390/h04739046.png" />-space [[#References|[2]]], [[#References|[3]]].
| + | {{TEX|auto}} |
| | + | {{TEX|done}} |
| | | | |
| − | The principal trends in the theory of Hilbert spaces with an indefinite metric are the same as those in general spaces with an indefinite metric, but with a considerable stress on the spectral theory. The geometry of Hilbert spaces with an indefinite metric is much richer than that of ordinary spaces with an indefinite metric. Thus, in the case of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/h/h047/h047390/h04739047.png" />-spaces there is an effective description of the maximal subspaces <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/h/h047/h047390/h04739048.png" /> among all the non-negative (non-positive, neutral) ones: these are the <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/h/h047/h047390/h04739049.png" />'s for which <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/h/h047/h047390/h04739050.png" /> (or, correspondingly, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/h/h047/h047390/h04739051.png" />; at least one of these equalities must be valid). Hence the analogue of the law of inertia of quadratic forms: If <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/h/h047/h047390/h04739052.png" /> is the canonical decomposition of the <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/h/h047/h047390/h04739053.png" />-space into a sum of semi-definite subspaces, then <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/h/h047/h047390/h04739054.png" />. The subspace <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/h/h047/h047390/h04739055.png" /> is maximal and non-negative if and only if <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/h/h047/h047390/h04739056.png" /> has an angular operator <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/h/h047/h047390/h04739057.png" /> with respect to <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/h/h047/h047390/h04739058.png" />, i.e. if <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/h/h047/h047390/h04739059.png" /> and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/h/h047/h047390/h04739060.png" />.
| + | A [[Hilbert space|Hilbert space]] $ E $ |
| | + | over the field of complex numbers endowed with a continuous bilinear (more exactly, sesquilinear) form $ G $ |
| | + | that is not, generally speaking, positive definite. The form $ G $ |
| | + | is often referred to as the $ G $- |
| | + | metric. The most important example of a Hilbert space with an indefinite metric is a so-called $ J $- |
| | + | space — a Hilbert space with an indefinite metric in which $ G $ |
| | + | is defined by a certain Hermitian involution $ J $ |
| | + | in $ E $ |
| | + | by the formula $ G( x, y) = ( Jx, y) $. |
| | + | The form $ G $ |
| | + | is then also denoted by the letter $ J $ |
| | + | and is called a $ J $- |
| | + | metric. The involution $ J $ |
| | + | may be represented as $ J = P _ {+} - P _ {-} $, |
| | + | where $ P _ {+} $ |
| | + | and $ P _ {-} $ |
| | + | are orthogonal projections in $ E $, |
| | + | and $ P _ {+} + P _ {-} = I $; |
| | + | the number $ \kappa = \min ( \mathop{\rm dim} P _ {+} , \mathop{\rm dim} P _ {-} ) $ |
| | + | is called the rank of indefiniteness of the $ J $- |
| | + | metric or of the $ J $- |
| | + | space. If $ \kappa < + \infty $, |
| | + | the Hilbert space with the indefinite metric $ ( E, J) $ |
| | + | is called a [[Pontryagin space|Pontryagin space]] $ \Pi _ \kappa $; |
| | + | see also [[Space with an indefinite metric|Space with an indefinite metric]]. |
| | | | |
| − | A theory of bases has been developed in <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/h/h047/h047390/h04739061.png" />-spaces; this theory helps in the study of the geometry of Hilbert spaces with an indefinite metric as well as of the operators on them. A <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/h/h047/h047390/h04739064.png" />-orthonormal basis of a <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/h/h047/h047390/h04739065.png" />-space <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/h/h047/h047390/h04739066.png" /> is a basis in the Hilbert space <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/h/h047/h047390/h04739067.png" /> satisfying the conditions <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/h/h047/h047390/h04739068.png" />; <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/h/h047/h047390/h04739069.png" />, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/h/h047/h047390/h04739070.png" />. For a <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/h/h047/h047390/h04739071.png" />-orthonormal sequence <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/h/h047/h047390/h04739072.png" /> to be a Riesz basis of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/h/h047/h047390/h04739073.png" /> it is necessary and sufficient that <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/h/h047/h047390/h04739074.png" />, where <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/h/h047/h047390/h04739075.png" /> is the closed linear hull of the vectors <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/h/h047/h047390/h04739076.png" />. If <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/h/h047/h047390/h04739077.png" /> is a <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/h/h047/h047390/h04739078.png" />-orthonormal basis in <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/h/h047/h047390/h04739079.png" />, then the decomposition <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/h/h047/h047390/h04739080.png" /> is the canonical decomposition of the <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/h/h047/h047390/h04739081.png" />-space <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/h/h047/h047390/h04739082.png" />. A large group of geometrical problems in Hilbert spaces with an indefinite metric are connected with the structure and properties of so-called dual pairs of subspaces of a Hilbert space with an indefinite metric <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/h/h047/h047390/h04739083.png" />, i.e. with pairs <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/h/h047/h047390/h04739084.png" /> of subspaces in <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/h/h047/h047390/h04739085.png" /> such that <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/h/h047/h047390/h04739086.png" /> and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/h/h047/h047390/h04739087.png" /> are mutually orthogonal, while <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/h/h047/h047390/h04739088.png" /> is a non-positive and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/h/h047/h047390/h04739089.png" /> is a non-negative space. A dual pair is said to be maximal if <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/h/h047/h047390/h04739090.png" /> and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/h/h047/h047390/h04739091.png" /> are maximal semi-definite subspaces. | + | Two Hilbert spaces $ ( E, G) $ |
| | + | and $ ( E _ {1} , G _ {1} ) $ |
| | + | with indefinite metrics are said to be metrically equivalent if there exists a linear homeomorphism $ U $ |
| | + | of $ E $ |
| | + | onto $ E _ {1} $ |
| | + | which transforms $ G $ |
| | + | to $ G _ {1} $. |
| | + | A $ G $- |
| | + | metric generated by an invertible Hermitian operator $ G $ |
| | + | by the formula $ G( x, y) = ( Gx, y) $ |
| | + | is said to be regular; after the introduction of a new scalar product that is metrically equivalent to the old one a regular $ G $- |
| | + | metric becomes a $ J $- |
| | + | metric. Any Hilbert space with an indefinite metric with a Hermitian form $ G $ |
| | + | may be $ G $- |
| | + | isometrically (i.e. with preservation of $ G $) |
| | + | imbedded in some $ J $- |
| | + | space [[#References|[2]]], [[#References|[3]]]. |
| | + | |
| | + | The principal trends in the theory of Hilbert spaces with an indefinite metric are the same as those in general spaces with an indefinite metric, but with a considerable stress on the spectral theory. The geometry of Hilbert spaces with an indefinite metric is much richer than that of ordinary spaces with an indefinite metric. Thus, in the case of $ J $- |
| | + | spaces there is an effective description of the maximal subspaces $ L $ |
| | + | among all the non-negative (non-positive, neutral) ones: these are the $ L $' |
| | + | s for which $ P _ {+} L = P _ {+} E $( |
| | + | or, correspondingly, $ P _ {-} L = P _ {-} E $; |
| | + | at least one of these equalities must be valid). Hence the analogue of the law of inertia of quadratic forms: If $ E = L _ {+} \dot{+} L _ {-} $ |
| | + | is the canonical decomposition of the $ J $- |
| | + | space into a sum of semi-definite subspaces, then $ \mathop{\rm dim} L _ \pm = \mathop{\rm dim} P _ \pm E $. |
| | + | The subspace $ L $ |
| | + | is maximal and non-negative if and only if $ L $ |
| | + | has an angular operator $ K $ |
| | + | with respect to $ E _ {+} $, |
| | + | i.e. if $ L = \{ {x + Kx } : {x \in E _ {+} } \} $ |
| | + | and $ \| K \| \leq 1 $. |
| | + | |
| | + | A theory of bases has been developed in $ J $- |
| | + | spaces; this theory helps in the study of the geometry of Hilbert spaces with an indefinite metric as well as of the operators on them. A $ J $- |
| | + | orthonormal basis of a $ J $- |
| | + | space $ ( E, J) $ |
| | + | is a basis in the Hilbert space $ E $ |
| | + | satisfying the conditions $ ( Je _ {k} , e _ {n} ) = \delta _ {kn} $; |
| | + | $ k $, |
| | + | $ n = 1, 2 ,\dots $. |
| | + | For a $ J $- |
| | + | orthonormal sequence $ {\mathcal E} $ |
| | + | to be a Riesz basis of $ E $ |
| | + | it is necessary and sufficient that $ E = M _ {+} \dot{+} M _ {-} $, |
| | + | where $ M _ \pm $ |
| | + | is the closed linear hull of the vectors $ \{ {e _ {k} } : {( Je _ {k} , e _ {k} ) = \pm 1 } \} $. |
| | + | If $ {\mathcal E} $ |
| | + | is a $ J $- |
| | + | orthonormal basis in $ E $, |
| | + | then the decomposition $ E = M _ {+} \dot{+} M _ {-} $ |
| | + | is the canonical decomposition of the $ J $- |
| | + | space $ E $. |
| | + | A large group of geometrical problems in Hilbert spaces with an indefinite metric are connected with the structure and properties of so-called dual pairs of subspaces of a Hilbert space with an indefinite metric $ ( E, J) $, |
| | + | i.e. with pairs $ N, P $ |
| | + | of subspaces in $ E $ |
| | + | such that $ N $ |
| | + | and $ P $ |
| | + | are mutually orthogonal, while $ N $ |
| | + | is a non-positive and $ P $ |
| | + | is a non-negative space. A dual pair is said to be maximal if $ N $ |
| | + | and $ P $ |
| | + | are maximal semi-definite subspaces. |
| | | | |
| | ==Theory of operators in a Hilbert space with an indefinite metric.== | | ==Theory of operators in a Hilbert space with an indefinite metric.== |
| − | The metric <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/h/h047/h047390/h04739092.png" /> is considered to be Hermitian and non-degenerate, while the operators that are considered are densely defined. For an operator <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/h/h047/h047390/h04739093.png" /> with domain of definition <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/h/h047/h047390/h04739094.png" /> let there be defined a <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/h/h047/h047390/h04739095.png" />-adjoint operator <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/h/h047/h047390/h04739096.png" /> by the equation | + | The metric $ G $ |
| | + | is considered to be Hermitian and non-degenerate, while the operators that are considered are densely defined. For an operator $ T $ |
| | + | with domain of definition $ D _ {T} $ |
| | + | let there be defined a $ G $- |
| | + | adjoint operator $ T ^ {c} $ |
| | + | by the equation |
| | | | |
| − | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/h/h047/h047390/h04739097.png" /></td> </tr></table>
| + | $$ |
| | + | G ( Tx, y) = \ |
| | + | G ( x, T ^ {c} y),\ \ |
| | + | y \in D _ {T} ,\ \ |
| | + | y \in D _ {T ^ {c} } . |
| | + | $$ |
| | | | |
| − | where <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/h/h047/h047390/h04739098.png" /> and | + | where $ T ^ {c} = G ^ {-1} T ^ {*} G $ |
| | + | and |
| | | | |
| − | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/h/h047/h047390/h04739099.png" /></td> </tr></table>
| + | $$ |
| | + | D _ {T ^ {c} } = G ^ {-1} \{ GE \cap T ^ {*- 1 } ( TE \cap GE) \} . |
| | + | $$ |
| | | | |
| − | An operator <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/h/h047/h047390/h047390100.png" /> is said to be <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/h/h047/h047390/h047390102.png" />-self-adjoint if <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/h/h047/h047390/h047390103.png" />, and is said to be <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/h/h047/h047390/h047390105.png" />-symmetric if <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/h/h047/h047390/h047390106.png" />, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/h/h047/h047390/h047390107.png" />. Root subspaces <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/h/h047/h047390/h047390108.png" /> and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/h/h047/h047390/h047390109.png" />, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/h/h047/h047390/h047390110.png" />, of a <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/h/h047/h047390/h047390111.png" />-symmetric operator <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/h/h047/h047390/h047390112.png" /> are <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/h/h047/h047390/h047390113.png" />-orthogonal; in particular, if <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/h/h047/h047390/h047390114.png" />, then <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/h/h047/h047390/h047390115.png" /> is a neutral subspace. | + | An operator $ T $ |
| | + | is said to be $ G $- |
| | + | self-adjoint if $ T = T ^ {c} $, |
| | + | and is said to be $ G $- |
| | + | symmetric if $ G( Tx, y) = G( x, Ty) $, |
| | + | $ x, y \in D _ {T} $. |
| | + | Root subspaces $ L _ \lambda ( T) $ |
| | + | and $ L _ \mu ( T) $, |
| | + | $ \lambda \neq \overline \mu \; $, |
| | + | of a $ G $- |
| | + | symmetric operator $ T $ |
| | + | are $ G $- |
| | + | orthogonal; in particular, if $ \lambda \neq \overline \lambda \; $, |
| | + | then $ L _ \lambda ( T) $ |
| | + | is a neutral subspace. |
| | | | |
| − | If <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/h/h047/h047390/h047390116.png" /> is a regular metric, then the spectrum <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/h/h047/h047390/h047390117.png" /> of the <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/h/h047/h047390/h047390118.png" />-self-adjoint operator <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/h/h047/h047390/h047390119.png" /> is symmetric with respect to the real axis; if it is not regular, this is usually not the case. The <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/h/h047/h047390/h047390120.png" />-self-adjointness of an operator <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/h/h047/h047390/h047390121.png" /> is equivalent to the self-adjointness of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/h/h047/h047390/h047390122.png" />. If <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/h/h047/h047390/h047390123.png" />, then the [[Cayley transform|Cayley transform]] <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/h/h047/h047390/h047390124.png" /> is a <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/h/h047/h047390/h047390126.png" />-unitary operator, i.e. is such that <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/h/h047/h047390/h047390127.png" />. The spectrum of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/h/h047/h047390/h047390128.png" /> is symmetric with respect to the circle <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/h/h047/h047390/h047390129.png" />. | + | If $ G $ |
| | + | is a regular metric, then the spectrum $ \sigma ( T) $ |
| | + | of the $ G $- |
| | + | self-adjoint operator $ T $ |
| | + | is symmetric with respect to the real axis; if it is not regular, this is usually not the case. The $ J $- |
| | + | self-adjointness of an operator $ T $ |
| | + | is equivalent to the self-adjointness of $ JT $. |
| | + | If $ \zeta , \overline \zeta \; \in \sigma ( T) $, |
| | + | then the [[Cayley transform]] $ U = ( T - \overline \zeta \; I) ( T - \zeta I ) ^ {-1} $ |
| | + | is a $ J $- |
| | + | unitary operator, i.e. is such that $ UJU ^ {*} = U ^ {*} JU = J $. |
| | + | The spectrum of $ U $ |
| | + | is symmetric with respect to the circle $ S = \{ {\lambda \in \mathbf C } : {| \lambda | = 1 } \} $. |
| | | | |
| − | Beginning with the study of L.S. Pontryagin [[#References|[1]]], the principal problem of the theory is the existence of semi-definite invariant subspaces. Let <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/h/h047/h047390/h047390130.png" /> be a bounded operator in a <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/h/h047/h047390/h047390131.png" />-space <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/h/h047/h047390/h047390132.png" /> and let <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/h/h047/h047390/h047390133.png" /> for <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/h/h047/h047390/h047390134.png" />, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/h/h047/h047390/h047390135.png" /> (the so-called plus-operator); if <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/h/h047/h047390/h047390136.png" /> is a [[Completely-continuous operator|completely-continuous operator]], then there exists a maximal non-negative <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/h/h047/h047390/h047390137.png" />-invariant subspace <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/h/h047/h047390/h047390138.png" />. This result is applicable, in particular, to <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/h/h047/h047390/h047390139.png" />-unitary operators <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/h/h047/h047390/h047390140.png" /> on the spaces <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/h/h047/h047390/h047390141.png" />, in which it is the base of the so-called definization method — a construction of an operator polynomial <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/h/h047/h047390/h047390142.png" /> that maps <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/h/h047/h047390/h047390143.png" /> into a semi-definite subspace. This method makes it possible to obtain, e.g., analogues of the ordinary spectral expansion for <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/h/h047/h047390/h047390144.png" />-unitary and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/h/h047/h047390/h047390145.png" />-self-adjoint operators on <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/h/h047/h047390/h047390146.png" />. | + | Beginning with the study of L.S. Pontryagin [[#References|[1]]], the principal problem of the theory is the existence of semi-definite invariant subspaces. Let $ T $ |
| | + | be a bounded operator in a $ J $- |
| | + | space $ E $ |
| | + | and let $ ( JTx, Tx) \geq 0 $ |
| | + | for $ ( Jx, x) \geq 0 $, |
| | + | $ x \in E $( |
| | + | the so-called plus-operator); if $ P _ {+} TP _ {-} $ |
| | + | is a [[Completely-continuous operator|completely-continuous operator]], then there exists a maximal non-negative $ T $- |
| | + | invariant subspace $ L $. |
| | + | This result is applicable, in particular, to $ J $- |
| | + | unitary operators $ U $ |
| | + | on the spaces $ \Pi _ \kappa $, |
| | + | in which it is the base of the so-called definization method — a construction of an operator polynomial $ p( U) $ |
| | + | that maps $ E $ |
| | + | into a semi-definite subspace. This method makes it possible to obtain, e.g., analogues of the ordinary spectral expansion for $ J $- |
| | + | unitary and $ J $- |
| | + | self-adjoint operators on $ \Pi _ \kappa $. |
| | | | |
| − | The theory of operators in Hilbert spaces with an indefinite metric is used in an essential way in the theory of canonical systems of ordinary differential equations; for example, the criterion of stability for such equations may be written as follows in terms of the [[Monodromy operator|monodromy operator]] <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/h/h047/h047390/h047390147.png" />: Stability holds if and only if a maximal <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/h/h047/h047390/h047390148.png" />-invariant dual pair of subspaces exists. Another important use of this theory is in the spectral theory of quadratic operator pencils, which is important in many problems of mathematical physics. | + | The theory of operators in Hilbert spaces with an indefinite metric is used in an essential way in the theory of canonical systems of ordinary differential equations; for example, the criterion of stability for such equations may be written as follows in terms of the [[Monodromy operator|monodromy operator]] $ U $: |
| | + | Stability holds if and only if a maximal $ U $- |
| | + | invariant dual pair of subspaces exists. Another important use of this theory is in the spectral theory of quadratic operator pencils, which is important in many problems of mathematical physics. |
| | | | |
| | For the theory of representations in Hilbert spaces with an indefinite metric see [[#References|[4]]]. | | For the theory of representations in Hilbert spaces with an indefinite metric see [[#References|[4]]]. |
| | | | |
| | ====References==== | | ====References==== |
| − | <table><TR><TD valign="top">[1]</TD> <TD valign="top"> L.S. Pontragin, "Hermitian operators in spaces with an indefinite metric" ''Izv. Akad. Nauk SSR Ser. Mat.'' , '''8''' (1944) pp. 243–280 (In Russian) (English abstract)</TD></TR><TR><TD valign="top">[2]</TD> <TD valign="top"> Yu.P. Ginzburg, I.S. Iokhvidov, "Investigations in the geometry of infinite-dimensional spaces with a bilinear metric" ''Russian Math. Surveys'' , '''17''' : 4 (1962) pp. 1–51 ''Uspekhi Mat. Nauk'' , '''17''' : 4 (1962) pp. 3–56</TD></TR><TR><TD valign="top">[3]</TD> <TD valign="top"> T.Ya. Azizov, I.S. Iokhvidov, "Linear operators in Hilbert spaces with a <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/h/h047/h047390/h047390149.png" />-metric" ''Russian Math. Surveys'' , '''26''' : 4 (1971) pp. 45–97 ''Uspekhi Mat. Nauk'' , '''26''' : 4 (1971) pp. 43–92</TD></TR><TR><TD valign="top">[4]</TD> <TD valign="top"> M.A. Naimark, R.S. Ismagilov, "Representations of groups and algebras in spaces with an indefinite metric" ''Itogi Nauk. Mat. Anal.'' (1969) pp. 73–105 (In Russian)</TD></TR><TR><TD valign="top">[5]</TD> <TD valign="top"> , ''Functional analysis'' , Moscow (1964) (In Russian)</TD></TR></table> | + | <table><TR><TD valign="top">[1]</TD> <TD valign="top"> L.S. Pontragin, "Hermitian operators in spaces with an indefinite metric" ''Izv. Akad. Nauk SSR Ser. Mat.'' , '''8''' (1944) pp. 243–280 (In Russian) (English abstract)</TD></TR><TR><TD valign="top">[2]</TD> <TD valign="top"> Yu.P. Ginzburg, I.S. Iokhvidov, "Investigations in the geometry of infinite-dimensional spaces with a bilinear metric" ''Russian Math. Surveys'' , '''17''' : 4 (1962) pp. 1–51 ''Uspekhi Mat. Nauk'' , '''17''' : 4 (1962) pp. 3–56</TD></TR><TR><TD valign="top">[3]</TD> <TD valign="top"> T.Ya. Azizov, I.S. Iokhvidov, "Linear operators in Hilbert spaces with a <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/h/h047/h047390/h047390149.png" />-metric" ''Russian Math. Surveys'' , '''26''' : 4 (1971) pp. 45–97 ''Uspekhi Mat. Nauk'' , '''26''' : 4 (1971) pp. 43–92 {{MR|288613}} {{ZBL|}} </TD></TR><TR><TD valign="top">[4]</TD> <TD valign="top"> M.A. Naimark, R.S. Ismagilov, "Representations of groups and algebras in spaces with an indefinite metric" ''Itogi Nauk. Mat. Anal.'' (1969) pp. 73–105 (In Russian) {{MR|415335}} {{ZBL|}} </TD></TR><TR><TD valign="top">[5]</TD> <TD valign="top"> , ''Functional analysis'' , Moscow (1964) (In Russian)</TD></TR></table> |
| − | | |
| − | | |
| | | | |
| | ====Comments==== | | ====Comments==== |
| − | Let <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/h/h047/h047390/h047390150.png" /> be a vector space over the complex numbers <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/h/h047/h047390/h047390151.png" />. A sesquilinear form on <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/h/h047/h047390/h047390152.png" /> is a complex-valued function <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/h/h047/h047390/h047390153.png" /> such that | + | Let $ V $ |
| | + | be a vector space over the complex numbers $ \mathbf C $. |
| | + | A sesquilinear form on $ V $ |
| | + | is a complex-valued function $ ( , ): V \times V \rightarrow \mathbf C $ |
| | + | such that |
| | | | |
| − | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/h/h047/h047390/h047390154.png" /></td> <td valign="top" style="width:5%;text-align:right;">(a1)</td></tr></table>
| + | $$ \tag{a1 } |
| | + | ( \alpha _ {1} x _ {1} + |
| | + | \alpha _ {2} x _ {2} , y) = \ |
| | + | \alpha _ {1} ( x _ {1} , y) + |
| | + | \alpha _ {2} ( x _ {2} , y) , |
| | + | $$ |
| | | | |
| − | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/h/h047/h047390/h047390155.png" /></td> <td valign="top" style="width:5%;text-align:right;">(a2)</td></tr></table>
| + | $$ \tag{a2 } |
| | + | \overline{ {( x, y ) }}\; = ( y, x) , |
| | + | $$ |
| | | | |
| − | for all <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/h/h047/h047390/h047390156.png" />; <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/h/h047/h047390/h047390157.png" />. Here the bar denotes complex conjugation. A vector space <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/h/h047/h047390/h047390158.png" /> provided with such a form is called an inner product space. In an inner product space one distinguishes positive, negative and neutral elements, defined, respectively, by the conditions <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/h/h047/h047390/h047390159.png" />, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/h/h047/h047390/h047390160.png" />, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/h/h047/h047390/h047390161.png" />. An indefinite inner product space is one which has both positive and negative elements. | + | for all $ x _ {1} , x _ {2} , x, y \in V $; |
| | + | $ \alpha _ {1} , \alpha _ {2} \in \mathbf C $. |
| | + | Here the bar denotes complex conjugation. A vector space $ V $ |
| | + | provided with such a form is called an inner product space. In an inner product space one distinguishes positive, negative and neutral elements, defined, respectively, by the conditions $ ( x, x) > 0 $, |
| | + | $ ( x, x) < 0 $, |
| | + | $ ( x, x) = 0 $. |
| | + | An indefinite inner product space is one which has both positive and negative elements. |
| | | | |
| − | The isotropic vectors of an inner product space <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/h/h047/h047390/h047390162.png" /> are the elements of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/h/h047/h047390/h047390163.png" />. The subspace <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/h/h047/h047390/h047390164.png" /> is called the isotropic part of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/h/h047/h047390/h047390165.png" />. An inner product space is non-degenerate if its isotropic part is zero. | + | The isotropic vectors of an inner product space $ V $ |
| | + | are the elements of $ V ^ \perp = \{ {x \in V } : {( x, y) = 0 \textrm{ for all } y \in V } \} $. |
| | + | The subspace $ V ^ \perp $ |
| | + | is called the isotropic part of $ V $. |
| | + | An inner product space is non-degenerate if its isotropic part is zero. |
| | | | |
| | An inner product space is decomposable if it can be represented as an orthogonal direct sum | | An inner product space is decomposable if it can be represented as an orthogonal direct sum |
| | | | |
| − | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/h/h047/h047390/h047390166.png" /></td> <td valign="top" style="width:5%;text-align:right;">(a3)</td></tr></table>
| + | $$ \tag{a3 } |
| | + | V = V ^ {+} \oplus V ^ {0} \oplus V ^ {-} |
| | + | $$ |
| | | | |
| − | with <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/h/h047/h047390/h047390167.png" /> consisting of neutral elements; <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/h/h047/h047390/h047390168.png" /> or <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/h/h047/h047390/h047390169.png" />; <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/h/h047/h047390/h047390170.png" /> or <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/h/h047/h047390/h047390171.png" />. The space <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/h/h047/h047390/h047390172.png" /> is then necessarily the isotropic part of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/h/h047/h047390/h047390173.png" />. Not every inner product space is decomposable, but every finite-dimensional one is decomposable. Every decomposition such as (a3) is called a fundamental decomposition. | + | with $ V ^ {0} $ |
| | + | consisting of neutral elements; $ x \in V ^ {+} \Rightarrow ( x, x) > 0 $ |
| | + | or $ x = 0 $; |
| | + | $ x \in V ^ {-} \Rightarrow ( x, x) < 0 $ |
| | + | or $ x = 0 $. |
| | + | The space $ V ^ {0} $ |
| | + | is then necessarily the isotropic part of $ V $. |
| | + | Not every inner product space is decomposable, but every finite-dimensional one is decomposable. Every decomposition such as (a3) is called a fundamental decomposition. |
| | | | |
| − | A definite subspace of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/h/h047/h047390/h047390174.png" /> is a subspace <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/h/h047/h047390/h047390175.png" /> such that the restriction of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/h/h047/h047390/h047390176.png" /> to <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/h/h047/h047390/h047390177.png" /> is either positive definite or negative definite. On such a subspace <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/h/h047/h047390/h047390178.png" />, the function <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/h/h047/h047390/h047390179.png" /> defines a norm. A definite subspace <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/h/h047/h047390/h047390180.png" /> is called intrinsically complete if it is complete in the topology defined by this norm. | + | A definite subspace of $ V $ |
| | + | is a subspace $ U $ |
| | + | such that the restriction of $ ( , ) $ |
| | + | to $ U $ |
| | + | is either positive definite or negative definite. On such a subspace $ U $, |
| | + | the function $ | x | _ {U} = | ( x, x) | ^ {1/2} $ |
| | + | defines a norm. A definite subspace $ U $ |
| | + | is called intrinsically complete if it is complete in the topology defined by this norm. |
| | | | |
| | A Krein space is a non-degenerate inner product space that admits a fundamental decomposition | | A Krein space is a non-degenerate inner product space that admits a fundamental decomposition |
| | | | |
| − | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/h/h047/h047390/h047390181.png" /></td> <td valign="top" style="width:5%;text-align:right;">(a4)</td></tr></table>
| + | $$ \tag{a4 } |
| | + | V = V ^ {+} \oplus V ^ {-} |
| | + | $$ |
| | | | |
| − | such that both <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/h/h047/h047390/h047390182.png" /> and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/h/h047/h047390/h047390183.png" /> are intrinsically complete (and then that is the case for every fundamental decomposition). | + | such that both $ V ^ {+} $ |
| | + | and $ V ^ {-} $ |
| | + | are intrinsically complete (and then that is the case for every fundamental decomposition). |
| | | | |
| − | These are the most important types of inner product spaces. A Pontryagin space is a special kind of Krein space, viz. a Krein space for which the dimension of one of the two components in a fundamental decomposition (a4) is equal to <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/h/h047/h047390/h047390184.png" /> (and then that is the case for every fundamental decomposition). | + | These are the most important types of inner product spaces. A Pontryagin space is a special kind of Krein space, viz. a Krein space for which the dimension of one of the two components in a fundamental decomposition (a4) is equal to $ n < \infty $( |
| | + | and then that is the case for every fundamental decomposition). |
| | | | |
| | For the geometry and operator theory of Krein spaces cf. [[Krein space|Krein space]] and [[#References|[a1]]]–[[#References|[a5]]]. For applications cf., e.g., [[#References|[a6]]]–[[#References|[a8]]]. | | For the geometry and operator theory of Krein spaces cf. [[Krein space|Krein space]] and [[#References|[a1]]]–[[#References|[a5]]]. For applications cf., e.g., [[#References|[a6]]]–[[#References|[a8]]]. |
| | | | |
| − | The phrase "inner product space" is also used in the more restricted sense of a vector space <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/h/h047/h047390/h047390185.png" /> equipped with a sesquilinear form such that besides (a1) and (a2) also the conditions (a5) and (a6) below hold. | + | The phrase "inner product space" is also used in the more restricted sense of a vector space $ V $ |
| | + | equipped with a sesquilinear form such that besides (a1) and (a2) also the conditions (a5) and (a6) below hold. |
| | | | |
| − | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/h/h047/h047390/h047390186.png" /></td> <td valign="top" style="width:5%;text-align:right;">(a5)</td></tr></table>
| + | $$ \tag{a5 } |
| | + | ( x, x) \geq 0 \ \ |
| | + | \textrm{ for } \textrm{ all } x \in V , |
| | + | $$ |
| | | | |
| − | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/h/h047/h047390/h047390187.png" /></td> <td valign="top" style="width:5%;text-align:right;">(a6)</td></tr></table>
| + | $$ \tag{a6 } |
| | + | ( x, x) = 0 \iff x = 0 . |
| | + | $$ |
| | | | |
| − | I.e. in the sense of a pre-Hilbert space. In case the sesquilinear form only satisfies (a1), (a2), (a5) the phrase "pre-inner product" is used. A space with a sesquilinear form such that (a1) and (a2) hold is then called an indefinite inner product space [[#References|[a8]]]. Thus, a partial dictionary between [[#References|[a1]]] and [[#References|[a8]]] is: inner product — indefinite inner product; positive semi-definite inner product — pre-inner product; positive definite inner product — inner product. | + | I.e. in the sense of a pre-Hilbert space. In case the sesquilinear form only satisfies (a1), (a2), (a5) the phrase "pre-inner product" is used. A space with a sesquilinear form such that (a1) and (a2) hold is then called an indefinite inner product space [[#References|[a8]]]. Thus, a partial dictionary between [[#References|[a1]]] and [[#References|[a8]]] is: inner product — indefinite inner product; positive semi-definite inner product — pre-inner product; positive definite inner product — inner product. |
| | | | |
| − | Finally, the phrases "inner product" and "inner product space" are used in still another different meaning in the theory of quadratic forms in algebra and number theory, [[#References|[a9]]]. In that setting an inner product on a module <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/h/h047/h047390/h047390188.png" /> over a commutative ring <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/h/h047/h047390/h047390189.png" /> with unit is a bilinear mapping | + | Finally, the phrases "inner product" and "inner product space" are used in still another different meaning in the theory of quadratic forms in algebra and number theory, [[#References|[a9]]]. In that setting an inner product on a module $ M $ |
| | + | over a commutative ring $ R $ |
| | + | with unit is a bilinear mapping |
| | | | |
| − | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/h/h047/h047390/h047390190.png" /></td> </tr></table>
| + | $$ |
| | + | \beta : M \times M \rightarrow R |
| | + | $$ |
| | | | |
| − | such that the following strong non-degeneracy conditions are satisfied: the two homomorphisms <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/h/h047/h047390/h047390191.png" /> given by <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/h/h047/h047390/h047390192.png" />, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/h/h047/h047390/h047390193.png" />, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/h/h047/h047390/h047390194.png" />, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/h/h047/h047390/h047390195.png" /> are bijective. An inner product module is then a module provided with an inner product, and an inner product space is an inner product module <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/h/h047/h047390/h047390196.png" /> such that <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/h/h047/h047390/h047390197.png" /> is a [[Projective module|projective module]]. | + | such that the following strong non-degeneracy conditions are satisfied: the two homomorphisms $ M \rightarrow \mathop{\rm Hom} _ {R} ( M, R) $ |
| | + | given by $ x \mapsto \phi _ {x} $, |
| | + | $ \phi _ {x} ( y) = \beta ( x, y) $, |
| | + | $ y \mapsto \psi _ {y} $, |
| | + | $ \psi _ {y} ( x) = \beta ( x, y) $ |
| | + | are bijective. An inner product module is then a module provided with an inner product, and an inner product space is an inner product module $ ( M, \beta ) $ |
| | + | such that $ M $ |
| | + | is a [[Projective module|projective module]]. |
| | | | |
| − | In turn, [[#References|[a8]]], in the theory of Banach algebras an inner product module refers to a module <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/h/h047/h047390/h047390198.png" /> over a [[C*-algebra|<img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/h/h047/h047390/h047390199.png" />-algebra]] <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/h/h047/h047390/h047390200.png" />, provided with a mapping <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/h/h047/h047390/h047390201.png" /> such that | + | In turn, [[#References|[a8]]], in the theory of Banach algebras an inner product module refers to a module $ X $ |
| | + | over a [[C*-algebra| $ C ^ {*} $- |
| | + | algebra]] $ B $, |
| | + | provided with a mapping $ \langle , \rangle: X \times X \rightarrow B $ |
| | + | such that |
| | | | |
| − | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/h/h047/h047390/h047390202.png" /></td> <td valign="top" style="width:5%;text-align:right;">(a7)</td></tr></table>
| + | $$ \tag{a7 } |
| | + | \langle x, x\rangle \geq 0 , |
| | + | $$ |
| | | | |
| − | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/h/h047/h047390/h047390203.png" /></td> <td valign="top" style="width:5%;text-align:right;">(a8)</td></tr></table>
| + | $$ \tag{a8 } |
| | + | \langle x, x\rangle = 0 \iff x = 0 , |
| | + | $$ |
| | | | |
| − | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/h/h047/h047390/h047390204.png" /></td> <td valign="top" style="width:5%;text-align:right;">(a9)</td></tr></table>
| + | $$ \tag{a9 } |
| | + | \langle x, y\rangle = \langle y, x\rangle ^ {*} , |
| | + | $$ |
| | | | |
| − | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/h/h047/h047390/h047390205.png" /></td> <td valign="top" style="width:5%;text-align:right;">(a10)</td></tr></table>
| + | $$ \tag{a10 } |
| | + | \langle x _ {1} b _ {1} + x _ {2} b _ {2} , y\rangle = < x _ {1} , y> b _ {1} + \langle x _ {2} , y\rangle b _ {2} , |
| | + | $$ |
| | | | |
| − | for all <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/h/h047/h047390/h047390206.png" />; <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/h/h047/h047390/h047390207.png" />. Here <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/h/h047/h047390/h047390208.png" /> in the <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/h/h047/h047390/h047390209.png" />-algebra <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/h/h047/h047390/h047390210.png" /> is defined as usual: An element <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/h/h047/h047390/h047390212.png" /> is <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/h/h047/h047390/h047390213.png" /> if it is Hermitian (i.e. <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/h/h047/h047390/h047390215.png" />) and of the form <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/h/h047/h047390/h047390216.png" /> for some <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/h/h047/h047390/h047390217.png" />. | + | for all $ x, x _ {1} , x _ {2} , y \in X $; |
| | + | $ b _ {1} , b _ {2} \in B $. |
| | + | Here $ \geq 0 $ |
| | + | in the $ C ^ {*} $- |
| | + | algebra $ B $ |
| | + | is defined as usual: An element $ b \in B $ |
| | + | is $ \geq 0 $ |
| | + | if it is Hermitian (i.e. $ b ^ {*} = b $) |
| | + | and of the form $ b = aa ^ {*} $ |
| | + | for some $ a \in B $. |
| | | | |
| | ====References==== | | ====References==== |
| − | <table><TR><TD valign="top">[a1]</TD> <TD valign="top"> J. Bognár, "Indefinite inner product spaces" , Springer (1974)</TD></TR><TR><TD valign="top">[a2]</TD> <TD valign="top"> I.S. [I.S. Iokhvidov] Iohidov, M.G. Krein, H. Langer, "Introduction to the spectral theory of operators in spaces with an indefinite metric" , Akademie Verlag (1982)</TD></TR><TR><TD valign="top">[a3]</TD> <TD valign="top"> I. [I. Gokhberg] Gohberg, P. Lancaster, L. Rodman, "Matrices and indefinite scalar products" , Birkhäuser (1983)</TD></TR><TR><TD valign="top">[a4]</TD> <TD valign="top"> I.S. Iokhvidov, M.G. Krein, "Spectral theory of operators in spaces with an indefinite metric I" ''Transl. Amer. Math. Soc. (2)'' , '''13''' (1960) pp. 105–176 ''Trudy Moskov. Mat. Obshch.'' , '''5''' (1956) pp. 367–432</TD></TR><TR><TD valign="top">[a5]</TD> <TD valign="top"> I.S. Iokhvidov, M.G. Krein, "Spectral theory of operators in spaces with an indefinite metric II" ''Transl. Amer. Math. Soc. (2)'' , '''34''' (1963) pp. 283–374 ''Trudy Moskov. Mat. Obshch.'' , '''8''' (1959) pp. 413–496</TD></TR><TR><TD valign="top">[a6]</TD> <TD valign="top"> Yu.L. Daletskii, M.G. Krein, "Stability of solutions of differential equations in Banach space" , Amer. Math. Soc. (1974) (Translated from Russian)</TD></TR><TR><TD valign="top">[a7]</TD> <TD valign="top"> L. Bracci, G. Morchio, F. Strocchi, "Wigner's theorem on symmetries in indefinite metric spaces" ''Comm. Math. Phys.'' , '''41''' (1975) pp. 289–299</TD></TR><TR><TD valign="top">[a8]</TD> <TD valign="top"> V.I. Istrăţescu, "Inner product structures" , Reidel (1987)</TD></TR><TR><TD valign="top">[a9]</TD> <TD valign="top"> J. Milnor, D. Husemoller, "Symmetric bilinear forms" , Springer (1973) pp. 16</TD></TR><TR><TD valign="top">[a10]</TD> <TD valign="top"> T.Ya. Azizov, I.S. Iokhvidov, "Linear operators in spaces with indefinite metric and their applications" ''J. Soviet Math.'' , '''15''' (1981) pp. 438–490 ''Itogi Nauk. i Tekhn. Mat. Anal.'' , '''17''' : 4 (1979) pp. 113–205</TD></TR></table> | + | <table><TR><TD valign="top">[a1]</TD> <TD valign="top"> J. Bognár, "Indefinite inner product spaces" , Springer (1974) {{MR|0467261}} {{ZBL|0286.46028}} {{ZBL|0277.47024}} </TD></TR><TR><TD valign="top">[a2]</TD> <TD valign="top"> I.S. [I.S. Iokhvidov] Iohidov, M.G. Krein, H. Langer, "Introduction to the spectral theory of operators in spaces with an indefinite metric" , Akademie Verlag (1982) {{MR|691137}} {{ZBL|}} </TD></TR><TR><TD valign="top">[a3]</TD> <TD valign="top"> I. [I. Gokhberg] Gohberg, P. Lancaster, L. Rodman, "Matrices and indefinite scalar products" , Birkhäuser (1983) {{MR|0859708}} {{ZBL|0513.15006}} </TD></TR><TR><TD valign="top">[a4]</TD> <TD valign="top"> I.S. Iokhvidov, M.G. Krein, "Spectral theory of operators in spaces with an indefinite metric I" ''Transl. Amer. Math. Soc. (2)'' , '''13''' (1960) pp. 105–176 ''Trudy Moskov. Mat. Obshch.'' , '''5''' (1956) pp. 367–432 {{MR|113145}} {{ZBL|0089.10803}} </TD></TR><TR><TD valign="top">[a5]</TD> <TD valign="top"> I.S. Iokhvidov, M.G. Krein, "Spectral theory of operators in spaces with an indefinite metric II" ''Transl. Amer. Math. Soc. (2)'' , '''34''' (1963) pp. 283–374 ''Trudy Moskov. Mat. Obshch.'' , '''8''' (1959) pp. 413–496 {{MR|}} {{ZBL|0132.35602}} </TD></TR><TR><TD valign="top">[a6]</TD> <TD valign="top"> Yu.L. Daletskii, M.G. Krein, "Stability of solutions of differential equations in Banach space" , Amer. Math. Soc. (1974) (Translated from Russian) {{MR|0352638}} {{ZBL|}} </TD></TR><TR><TD valign="top">[a7]</TD> <TD valign="top"> L. Bracci, G. Morchio, F. Strocchi, "Wigner's theorem on symmetries in indefinite metric spaces" ''Comm. Math. Phys.'' , '''41''' (1975) pp. 289–299 {{MR|368648}} {{ZBL|}} </TD></TR><TR><TD valign="top">[a8]</TD> <TD valign="top"> V.I. Istrăţescu, "Inner product structures" , Reidel (1987) {{MR|0903846}} {{ZBL|0629.46027}} </TD></TR><TR><TD valign="top">[a9]</TD> <TD valign="top"> J. Milnor, D. Husemoller, "Symmetric bilinear forms" , Springer (1973) pp. 16 {{MR|0506372}} {{ZBL|0292.10016}} </TD></TR><TR><TD valign="top">[a10]</TD> <TD valign="top"> T.Ya. Azizov, I.S. Iokhvidov, "Linear operators in spaces with indefinite metric and their applications" ''J. Soviet Math.'' , '''15''' (1981) pp. 438–490 ''Itogi Nauk. i Tekhn. Mat. Anal.'' , '''17''' : 4 (1979) pp. 113–205 {{MR|}} {{ZBL|0478.47019}} </TD></TR></table> |
A Hilbert space $ E $
over the field of complex numbers endowed with a continuous bilinear (more exactly, sesquilinear) form $ G $
that is not, generally speaking, positive definite. The form $ G $
is often referred to as the $ G $-
metric. The most important example of a Hilbert space with an indefinite metric is a so-called $ J $-
space — a Hilbert space with an indefinite metric in which $ G $
is defined by a certain Hermitian involution $ J $
in $ E $
by the formula $ G( x, y) = ( Jx, y) $.
The form $ G $
is then also denoted by the letter $ J $
and is called a $ J $-
metric. The involution $ J $
may be represented as $ J = P _ {+} - P _ {-} $,
where $ P _ {+} $
and $ P _ {-} $
are orthogonal projections in $ E $,
and $ P _ {+} + P _ {-} = I $;
the number $ \kappa = \min ( \mathop{\rm dim} P _ {+} , \mathop{\rm dim} P _ {-} ) $
is called the rank of indefiniteness of the $ J $-
metric or of the $ J $-
space. If $ \kappa < + \infty $,
the Hilbert space with the indefinite metric $ ( E, J) $
is called a Pontryagin space $ \Pi _ \kappa $;
see also Space with an indefinite metric.
Two Hilbert spaces $ ( E, G) $
and $ ( E _ {1} , G _ {1} ) $
with indefinite metrics are said to be metrically equivalent if there exists a linear homeomorphism $ U $
of $ E $
onto $ E _ {1} $
which transforms $ G $
to $ G _ {1} $.
A $ G $-
metric generated by an invertible Hermitian operator $ G $
by the formula $ G( x, y) = ( Gx, y) $
is said to be regular; after the introduction of a new scalar product that is metrically equivalent to the old one a regular $ G $-
metric becomes a $ J $-
metric. Any Hilbert space with an indefinite metric with a Hermitian form $ G $
may be $ G $-
isometrically (i.e. with preservation of $ G $)
imbedded in some $ J $-
space [2], [3].
The principal trends in the theory of Hilbert spaces with an indefinite metric are the same as those in general spaces with an indefinite metric, but with a considerable stress on the spectral theory. The geometry of Hilbert spaces with an indefinite metric is much richer than that of ordinary spaces with an indefinite metric. Thus, in the case of $ J $-
spaces there is an effective description of the maximal subspaces $ L $
among all the non-negative (non-positive, neutral) ones: these are the $ L $'
s for which $ P _ {+} L = P _ {+} E $(
or, correspondingly, $ P _ {-} L = P _ {-} E $;
at least one of these equalities must be valid). Hence the analogue of the law of inertia of quadratic forms: If $ E = L _ {+} \dot{+} L _ {-} $
is the canonical decomposition of the $ J $-
space into a sum of semi-definite subspaces, then $ \mathop{\rm dim} L _ \pm = \mathop{\rm dim} P _ \pm E $.
The subspace $ L $
is maximal and non-negative if and only if $ L $
has an angular operator $ K $
with respect to $ E _ {+} $,
i.e. if $ L = \{ {x + Kx } : {x \in E _ {+} } \} $
and $ \| K \| \leq 1 $.
A theory of bases has been developed in $ J $-
spaces; this theory helps in the study of the geometry of Hilbert spaces with an indefinite metric as well as of the operators on them. A $ J $-
orthonormal basis of a $ J $-
space $ ( E, J) $
is a basis in the Hilbert space $ E $
satisfying the conditions $ ( Je _ {k} , e _ {n} ) = \delta _ {kn} $;
$ k $,
$ n = 1, 2 ,\dots $.
For a $ J $-
orthonormal sequence $ {\mathcal E} $
to be a Riesz basis of $ E $
it is necessary and sufficient that $ E = M _ {+} \dot{+} M _ {-} $,
where $ M _ \pm $
is the closed linear hull of the vectors $ \{ {e _ {k} } : {( Je _ {k} , e _ {k} ) = \pm 1 } \} $.
If $ {\mathcal E} $
is a $ J $-
orthonormal basis in $ E $,
then the decomposition $ E = M _ {+} \dot{+} M _ {-} $
is the canonical decomposition of the $ J $-
space $ E $.
A large group of geometrical problems in Hilbert spaces with an indefinite metric are connected with the structure and properties of so-called dual pairs of subspaces of a Hilbert space with an indefinite metric $ ( E, J) $,
i.e. with pairs $ N, P $
of subspaces in $ E $
such that $ N $
and $ P $
are mutually orthogonal, while $ N $
is a non-positive and $ P $
is a non-negative space. A dual pair is said to be maximal if $ N $
and $ P $
are maximal semi-definite subspaces.
Theory of operators in a Hilbert space with an indefinite metric.
The metric $ G $
is considered to be Hermitian and non-degenerate, while the operators that are considered are densely defined. For an operator $ T $
with domain of definition $ D _ {T} $
let there be defined a $ G $-
adjoint operator $ T ^ {c} $
by the equation
$$
G ( Tx, y) = \
G ( x, T ^ {c} y),\ \
y \in D _ {T} ,\ \
y \in D _ {T ^ {c} } .
$$
where $ T ^ {c} = G ^ {-1} T ^ {*} G $
and
$$
D _ {T ^ {c} } = G ^ {-1} \{ GE \cap T ^ {*- 1 } ( TE \cap GE) \} .
$$
An operator $ T $
is said to be $ G $-
self-adjoint if $ T = T ^ {c} $,
and is said to be $ G $-
symmetric if $ G( Tx, y) = G( x, Ty) $,
$ x, y \in D _ {T} $.
Root subspaces $ L _ \lambda ( T) $
and $ L _ \mu ( T) $,
$ \lambda \neq \overline \mu \; $,
of a $ G $-
symmetric operator $ T $
are $ G $-
orthogonal; in particular, if $ \lambda \neq \overline \lambda \; $,
then $ L _ \lambda ( T) $
is a neutral subspace.
If $ G $
is a regular metric, then the spectrum $ \sigma ( T) $
of the $ G $-
self-adjoint operator $ T $
is symmetric with respect to the real axis; if it is not regular, this is usually not the case. The $ J $-
self-adjointness of an operator $ T $
is equivalent to the self-adjointness of $ JT $.
If $ \zeta , \overline \zeta \; \in \sigma ( T) $,
then the Cayley transform $ U = ( T - \overline \zeta \; I) ( T - \zeta I ) ^ {-1} $
is a $ J $-
unitary operator, i.e. is such that $ UJU ^ {*} = U ^ {*} JU = J $.
The spectrum of $ U $
is symmetric with respect to the circle $ S = \{ {\lambda \in \mathbf C } : {| \lambda | = 1 } \} $.
Beginning with the study of L.S. Pontryagin [1], the principal problem of the theory is the existence of semi-definite invariant subspaces. Let $ T $
be a bounded operator in a $ J $-
space $ E $
and let $ ( JTx, Tx) \geq 0 $
for $ ( Jx, x) \geq 0 $,
$ x \in E $(
the so-called plus-operator); if $ P _ {+} TP _ {-} $
is a completely-continuous operator, then there exists a maximal non-negative $ T $-
invariant subspace $ L $.
This result is applicable, in particular, to $ J $-
unitary operators $ U $
on the spaces $ \Pi _ \kappa $,
in which it is the base of the so-called definization method — a construction of an operator polynomial $ p( U) $
that maps $ E $
into a semi-definite subspace. This method makes it possible to obtain, e.g., analogues of the ordinary spectral expansion for $ J $-
unitary and $ J $-
self-adjoint operators on $ \Pi _ \kappa $.
The theory of operators in Hilbert spaces with an indefinite metric is used in an essential way in the theory of canonical systems of ordinary differential equations; for example, the criterion of stability for such equations may be written as follows in terms of the monodromy operator $ U $:
Stability holds if and only if a maximal $ U $-
invariant dual pair of subspaces exists. Another important use of this theory is in the spectral theory of quadratic operator pencils, which is important in many problems of mathematical physics.
For the theory of representations in Hilbert spaces with an indefinite metric see [4].
References
| [1] | L.S. Pontragin, "Hermitian operators in spaces with an indefinite metric" Izv. Akad. Nauk SSR Ser. Mat. , 8 (1944) pp. 243–280 (In Russian) (English abstract) |
| [2] | Yu.P. Ginzburg, I.S. Iokhvidov, "Investigations in the geometry of infinite-dimensional spaces with a bilinear metric" Russian Math. Surveys , 17 : 4 (1962) pp. 1–51 Uspekhi Mat. Nauk , 17 : 4 (1962) pp. 3–56 |
| [3] | T.Ya. Azizov, I.S. Iokhvidov, "Linear operators in Hilbert spaces with a 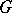 -metric" Russian Math. Surveys , 26 : 4 (1971) pp. 45–97 Uspekhi Mat. Nauk , 26 : 4 (1971) pp. 43–92 MR288613 -metric" Russian Math. Surveys , 26 : 4 (1971) pp. 45–97 Uspekhi Mat. Nauk , 26 : 4 (1971) pp. 43–92 MR288613 |
| [4] | M.A. Naimark, R.S. Ismagilov, "Representations of groups and algebras in spaces with an indefinite metric" Itogi Nauk. Mat. Anal. (1969) pp. 73–105 (In Russian) MR415335 |
| [5] | , Functional analysis , Moscow (1964) (In Russian) |
Let $ V $
be a vector space over the complex numbers $ \mathbf C $.
A sesquilinear form on $ V $
is a complex-valued function $ ( , ): V \times V \rightarrow \mathbf C $
such that
$$ \tag{a1 }
( \alpha _ {1} x _ {1} +
\alpha _ {2} x _ {2} , y) = \
\alpha _ {1} ( x _ {1} , y) +
\alpha _ {2} ( x _ {2} , y) ,
$$
$$ \tag{a2 }
\overline{ {( x, y ) }}\; = ( y, x) ,
$$
for all $ x _ {1} , x _ {2} , x, y \in V $;
$ \alpha _ {1} , \alpha _ {2} \in \mathbf C $.
Here the bar denotes complex conjugation. A vector space $ V $
provided with such a form is called an inner product space. In an inner product space one distinguishes positive, negative and neutral elements, defined, respectively, by the conditions $ ( x, x) > 0 $,
$ ( x, x) < 0 $,
$ ( x, x) = 0 $.
An indefinite inner product space is one which has both positive and negative elements.
The isotropic vectors of an inner product space $ V $
are the elements of $ V ^ \perp = \{ {x \in V } : {( x, y) = 0 \textrm{ for all } y \in V } \} $.
The subspace $ V ^ \perp $
is called the isotropic part of $ V $.
An inner product space is non-degenerate if its isotropic part is zero.
An inner product space is decomposable if it can be represented as an orthogonal direct sum
$$ \tag{a3 }
V = V ^ {+} \oplus V ^ {0} \oplus V ^ {-}
$$
with $ V ^ {0} $
consisting of neutral elements; $ x \in V ^ {+} \Rightarrow ( x, x) > 0 $
or $ x = 0 $;
$ x \in V ^ {-} \Rightarrow ( x, x) < 0 $
or $ x = 0 $.
The space $ V ^ {0} $
is then necessarily the isotropic part of $ V $.
Not every inner product space is decomposable, but every finite-dimensional one is decomposable. Every decomposition such as (a3) is called a fundamental decomposition.
A definite subspace of $ V $
is a subspace $ U $
such that the restriction of $ ( , ) $
to $ U $
is either positive definite or negative definite. On such a subspace $ U $,
the function $ | x | _ {U} = | ( x, x) | ^ {1/2} $
defines a norm. A definite subspace $ U $
is called intrinsically complete if it is complete in the topology defined by this norm.
A Krein space is a non-degenerate inner product space that admits a fundamental decomposition
$$ \tag{a4 }
V = V ^ {+} \oplus V ^ {-}
$$
such that both $ V ^ {+} $
and $ V ^ {-} $
are intrinsically complete (and then that is the case for every fundamental decomposition).
These are the most important types of inner product spaces. A Pontryagin space is a special kind of Krein space, viz. a Krein space for which the dimension of one of the two components in a fundamental decomposition (a4) is equal to $ n < \infty $(
and then that is the case for every fundamental decomposition).
For the geometry and operator theory of Krein spaces cf. Krein space and [a1]–[a5]. For applications cf., e.g., [a6]–[a8].
The phrase "inner product space" is also used in the more restricted sense of a vector space $ V $
equipped with a sesquilinear form such that besides (a1) and (a2) also the conditions (a5) and (a6) below hold.
$$ \tag{a5 }
( x, x) \geq 0 \ \
\textrm{ for } \textrm{ all } x \in V ,
$$
$$ \tag{a6 }
( x, x) = 0 \iff x = 0 .
$$
I.e. in the sense of a pre-Hilbert space. In case the sesquilinear form only satisfies (a1), (a2), (a5) the phrase "pre-inner product" is used. A space with a sesquilinear form such that (a1) and (a2) hold is then called an indefinite inner product space [a8]. Thus, a partial dictionary between [a1] and [a8] is: inner product — indefinite inner product; positive semi-definite inner product — pre-inner product; positive definite inner product — inner product.
Finally, the phrases "inner product" and "inner product space" are used in still another different meaning in the theory of quadratic forms in algebra and number theory, [a9]. In that setting an inner product on a module $ M $
over a commutative ring $ R $
with unit is a bilinear mapping
$$
\beta : M \times M \rightarrow R
$$
such that the following strong non-degeneracy conditions are satisfied: the two homomorphisms $ M \rightarrow \mathop{\rm Hom} _ {R} ( M, R) $
given by $ x \mapsto \phi _ {x} $,
$ \phi _ {x} ( y) = \beta ( x, y) $,
$ y \mapsto \psi _ {y} $,
$ \psi _ {y} ( x) = \beta ( x, y) $
are bijective. An inner product module is then a module provided with an inner product, and an inner product space is an inner product module $ ( M, \beta ) $
such that $ M $
is a projective module.
In turn, [a8], in the theory of Banach algebras an inner product module refers to a module $ X $
over a $ C ^ {*} $-
algebra $ B $,
provided with a mapping $ \langle , \rangle: X \times X \rightarrow B $
such that
$$ \tag{a7 }
\langle x, x\rangle \geq 0 ,
$$
$$ \tag{a8 }
\langle x, x\rangle = 0 \iff x = 0 ,
$$
$$ \tag{a9 }
\langle x, y\rangle = \langle y, x\rangle ^ {*} ,
$$
$$ \tag{a10 }
\langle x _ {1} b _ {1} + x _ {2} b _ {2} , y\rangle = < x _ {1} , y> b _ {1} + \langle x _ {2} , y\rangle b _ {2} ,
$$
for all $ x, x _ {1} , x _ {2} , y \in X $;
$ b _ {1} , b _ {2} \in B $.
Here $ \geq 0 $
in the $ C ^ {*} $-
algebra $ B $
is defined as usual: An element $ b \in B $
is $ \geq 0 $
if it is Hermitian (i.e. $ b ^ {*} = b $)
and of the form $ b = aa ^ {*} $
for some $ a \in B $.
References
| [a1] | J. Bognár, "Indefinite inner product spaces" , Springer (1974) MR0467261 Zbl 0286.46028 Zbl 0277.47024 |
| [a2] | I.S. [I.S. Iokhvidov] Iohidov, M.G. Krein, H. Langer, "Introduction to the spectral theory of operators in spaces with an indefinite metric" , Akademie Verlag (1982) MR691137 |
| [a3] | I. [I. Gokhberg] Gohberg, P. Lancaster, L. Rodman, "Matrices and indefinite scalar products" , Birkhäuser (1983) MR0859708 Zbl 0513.15006 |
| [a4] | I.S. Iokhvidov, M.G. Krein, "Spectral theory of operators in spaces with an indefinite metric I" Transl. Amer. Math. Soc. (2) , 13 (1960) pp. 105–176 Trudy Moskov. Mat. Obshch. , 5 (1956) pp. 367–432 MR113145 Zbl 0089.10803 |
| [a5] | I.S. Iokhvidov, M.G. Krein, "Spectral theory of operators in spaces with an indefinite metric II" Transl. Amer. Math. Soc. (2) , 34 (1963) pp. 283–374 Trudy Moskov. Mat. Obshch. , 8 (1959) pp. 413–496 Zbl 0132.35602 |
| [a6] | Yu.L. Daletskii, M.G. Krein, "Stability of solutions of differential equations in Banach space" , Amer. Math. Soc. (1974) (Translated from Russian) MR0352638 |
| [a7] | L. Bracci, G. Morchio, F. Strocchi, "Wigner's theorem on symmetries in indefinite metric spaces" Comm. Math. Phys. , 41 (1975) pp. 289–299 MR368648 |
| [a8] | V.I. Istrăţescu, "Inner product structures" , Reidel (1987) MR0903846 Zbl 0629.46027 |
| [a9] | J. Milnor, D. Husemoller, "Symmetric bilinear forms" , Springer (1973) pp. 16 MR0506372 Zbl 0292.10016 |
| [a10] | T.Ya. Azizov, I.S. Iokhvidov, "Linear operators in spaces with indefinite metric and their applications" J. Soviet Math. , 15 (1981) pp. 438–490 Itogi Nauk. i Tekhn. Mat. Anal. , 17 : 4 (1979) pp. 113–205 Zbl 0478.47019 |
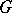 -metric" Russian Math. Surveys , 26 : 4 (1971) pp. 45–97 Uspekhi Mat. Nauk , 26 : 4 (1971) pp. 43–92 MR288613
-metric" Russian Math. Surveys , 26 : 4 (1971) pp. 45–97 Uspekhi Mat. Nauk , 26 : 4 (1971) pp. 43–92 MR288613