Difference between revisions of "BCI-algebra"
(Importing text file) |
m |
||
| Line 1: | Line 1: | ||
| − | Algebras introduced by K. Iséki in [[#References|[a4]]] as a generalized version of BCK-algebras (cf. [[BCK-algebra|BCK-algebra]]). The latter were developed by Iséki and S. Tannaka in [[#References|[a6]]] to generalize the set difference in set theory, and by Y. Imai and Iséki in [[#References|[a3]]] as the algebras of certain propositional calculi. It turns out that Abelian groups (cf. [[Abelian group|Abelian group]]) are a special case of BCI-algebras. One may take different axiom systems for BCI-algebras, and one such system says that a BCI-algebra is a non-empty set | + | Algebras introduced by K. Iséki in [[#References|[a4]]] as a generalized version of BCK-algebras (cf. [[BCK-algebra|BCK-algebra]]). The latter were developed by Iséki and S. Tannaka in [[#References|[a6]]] to generalize the set difference in set theory, and by Y. Imai and Iséki in [[#References|[a3]]] as the algebras of certain propositional calculi. It turns out that Abelian groups (cf. [[Abelian group|Abelian group]]) are a special case of BCI-algebras. One may take different axiom systems for BCI-algebras, and one such system says that a BCI-algebra is a non-empty set $X$ with a [[binary relation]] $\star$ and a constant $0$ satisfying |
i) <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b110/b110180/b1101804.png" />; | i) <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b110/b110180/b1101804.png" />; | ||
| Line 5: | Line 5: | ||
ii) <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b110/b110180/b1101805.png" />; | ii) <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b110/b110180/b1101805.png" />; | ||
| − | iii) | + | iii) $x \star x = 0$; |
iv) <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b110/b110180/b1101807.png" /> and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b110/b110180/b1101808.png" /> imply that <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b110/b110180/b1101809.png" />; | iv) <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b110/b110180/b1101807.png" /> and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b110/b110180/b1101808.png" /> imply that <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b110/b110180/b1101809.png" />; | ||
| Line 19: | Line 19: | ||
====References==== | ====References==== | ||
<table><TR><TD valign="top">[a1]</TD> <TD valign="top"> C.S. Hoo, "Fuzzy ideals of BCI and MV-algebras" ''Fuzzy Sets and Systems'' , '''62''' (1994) pp. 111–114</TD></TR><TR><TD valign="top">[a2]</TD> <TD valign="top"> C.S. Hoo, "Fuzzy implicative and Boolean ideals of MV-algebras" ''Fuzzy Sets and Systems'' , '''66''' (1994) pp. 315–327</TD></TR><TR><TD valign="top">[a3]</TD> <TD valign="top"> Y. Imai, K. Iséki, "On axiom systems of propositional calculi, XIV" ''Proc. Japan Acad. Ser. A, Math. Sci.'' , '''42''' (1966) pp. 19–22</TD></TR><TR><TD valign="top">[a4]</TD> <TD valign="top"> K. Iséki, "An algebra related with a propositional calculus" ''Proc. Japan Acad. Ser. A, Math. Sci.'' , '''42''' (1966) pp. 26–29</TD></TR><TR><TD valign="top">[a5]</TD> <TD valign="top"> K. Iséki, "On BCI-algebras" ''Math. Seminar Notes (Kobe University)'' , '''8''' (1980) pp. 125–130</TD></TR><TR><TD valign="top">[a6]</TD> <TD valign="top"> K. Iséki, S. Tanaka, "An introduction to the theory of BCK-algebras" ''Math. Japon.'' , '''23''' (1978) pp. 1–26</TD></TR></table> | <table><TR><TD valign="top">[a1]</TD> <TD valign="top"> C.S. Hoo, "Fuzzy ideals of BCI and MV-algebras" ''Fuzzy Sets and Systems'' , '''62''' (1994) pp. 111–114</TD></TR><TR><TD valign="top">[a2]</TD> <TD valign="top"> C.S. Hoo, "Fuzzy implicative and Boolean ideals of MV-algebras" ''Fuzzy Sets and Systems'' , '''66''' (1994) pp. 315–327</TD></TR><TR><TD valign="top">[a3]</TD> <TD valign="top"> Y. Imai, K. Iséki, "On axiom systems of propositional calculi, XIV" ''Proc. Japan Acad. Ser. A, Math. Sci.'' , '''42''' (1966) pp. 19–22</TD></TR><TR><TD valign="top">[a4]</TD> <TD valign="top"> K. Iséki, "An algebra related with a propositional calculus" ''Proc. Japan Acad. Ser. A, Math. Sci.'' , '''42''' (1966) pp. 26–29</TD></TR><TR><TD valign="top">[a5]</TD> <TD valign="top"> K. Iséki, "On BCI-algebras" ''Math. Seminar Notes (Kobe University)'' , '''8''' (1980) pp. 125–130</TD></TR><TR><TD valign="top">[a6]</TD> <TD valign="top"> K. Iséki, S. Tanaka, "An introduction to the theory of BCK-algebras" ''Math. Japon.'' , '''23''' (1978) pp. 1–26</TD></TR></table> | ||
| + | |||
| + | {{TEX|want}} | ||
Revision as of 20:25, 13 December 2023
Algebras introduced by K. Iséki in [a4] as a generalized version of BCK-algebras (cf. BCK-algebra). The latter were developed by Iséki and S. Tannaka in [a6] to generalize the set difference in set theory, and by Y. Imai and Iséki in [a3] as the algebras of certain propositional calculi. It turns out that Abelian groups (cf. Abelian group) are a special case of BCI-algebras. One may take different axiom systems for BCI-algebras, and one such system says that a BCI-algebra is a non-empty set $X$ with a binary relation $\star$ and a constant $0$ satisfying
i) 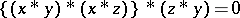 ;
;
ii) 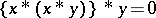 ;
;
iii) $x \star x = 0$;
iv) 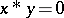 and
and 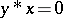 imply that
imply that  ;
;
v) 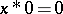 implies that
implies that 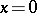 . A partial order
. A partial order 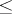 may be defined by
may be defined by 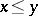 if and only if
if and only if  . A very useful identity satisfied by
. A very useful identity satisfied by 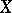 is
is 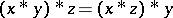 . One can then develop many of the usual algebraic concepts. An ideal is a set
. One can then develop many of the usual algebraic concepts. An ideal is a set 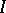 with the properties that
with the properties that 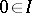 and that whenever
and that whenever 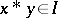 and
and 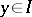 , then
, then  . The ideal is implicative if
. The ideal is implicative if 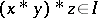 and
and 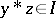 imply that
imply that 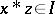 . It is known that one always has
. It is known that one always has 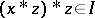 . An ideal
. An ideal 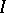 is closed if whenever
is closed if whenever 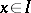 then
then 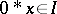 . While ideals in general are not subalgebras, closed ideals are. A subalgebra simply means a subset containing
. While ideals in general are not subalgebras, closed ideals are. A subalgebra simply means a subset containing  and closed under
and closed under  that is itself a BCI-algebra under
that is itself a BCI-algebra under  .
.
The subset 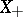 of all elements
of all elements 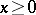 forms an ideal, called the
forms an ideal, called the 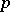 -radical of
-radical of 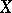 . The algebra
. The algebra 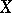 is a BCK-algebra if and only if
is a BCK-algebra if and only if 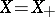 , and
, and 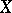 is
is 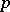 -semi-simple if and only if
-semi-simple if and only if 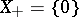 . In the latter case,
. In the latter case, 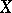 satisfies the identity
satisfies the identity 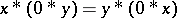 for all
for all  and
and  . It then follows that one can define an operation
. It then follows that one can define an operation 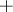 on
on 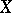 by
by 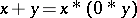 , and
, and 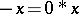 . This makes
. This makes 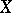 into an Abelian group with
into an Abelian group with  as the identity. Conversely, every Abelian group
as the identity. Conversely, every Abelian group 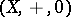 can be given a BCI-algebra structure by
can be given a BCI-algebra structure by  . It follows that the category of Abelian groups is equivalent to the subcategory of the category of BCI-algebras formed by the
. It follows that the category of Abelian groups is equivalent to the subcategory of the category of BCI-algebras formed by the 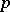 -semi-simple BCI-algebras. Here, a homomorphism
-semi-simple BCI-algebras. Here, a homomorphism 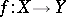 from one BCI-algebra to another is a function satisfying
from one BCI-algebra to another is a function satisfying 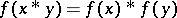 . In general,
. In general, 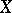 always contains a
always contains a 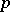 -semi-simple BCI-subalgebra, namely its
-semi-simple BCI-subalgebra, namely its 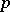 -semi-simple part
-semi-simple part 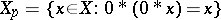 . Of course, also
. Of course, also 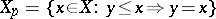 , since it can be verified easily that the induced partial order in a
, since it can be verified easily that the induced partial order in a 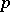 -semi-simple BCI-algebra is always trivial. Clearly,
-semi-simple BCI-algebra is always trivial. Clearly, 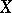 is
is 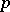 -semi-simple if
-semi-simple if 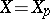 , and
, and 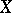 is a BCK-algebra if
is a BCK-algebra if 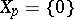 . Note that for a
. Note that for a 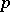 -semi-simple BCI-algebra, the closed ideals are precisely the subgroups of the associated Abelian group structure.
-semi-simple BCI-algebra, the closed ideals are precisely the subgroups of the associated Abelian group structure.
Some of the homological algebra properties of BCI-algebras are known. For example, it is known that a BCI-algebra is injective if and only if it is 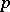 -semi-simple and its associated Abelian group structure is divisible (cf, also Divisible group).
-semi-simple and its associated Abelian group structure is divisible (cf, also Divisible group).
Fuzzy ideals of BCI-algebras are described in [a1] and [a2].
References
| [a1] | C.S. Hoo, "Fuzzy ideals of BCI and MV-algebras" Fuzzy Sets and Systems , 62 (1994) pp. 111–114 |
| [a2] | C.S. Hoo, "Fuzzy implicative and Boolean ideals of MV-algebras" Fuzzy Sets and Systems , 66 (1994) pp. 315–327 |
| [a3] | Y. Imai, K. Iséki, "On axiom systems of propositional calculi, XIV" Proc. Japan Acad. Ser. A, Math. Sci. , 42 (1966) pp. 19–22 |
| [a4] | K. Iséki, "An algebra related with a propositional calculus" Proc. Japan Acad. Ser. A, Math. Sci. , 42 (1966) pp. 26–29 |
| [a5] | K. Iséki, "On BCI-algebras" Math. Seminar Notes (Kobe University) , 8 (1980) pp. 125–130 |
| [a6] | K. Iséki, S. Tanaka, "An introduction to the theory of BCK-algebras" Math. Japon. , 23 (1978) pp. 1–26 |
BCI-algebra. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=BCI-algebra&oldid=12055