Difference between revisions of "Helicoid"
(Importing text file) |
(image) |
||
| (3 intermediate revisions by 2 users not shown) | |||
| Line 1: | Line 1: | ||
| − | + | {{TEX|done}} | |
| + | {{MSC|53A10|49Q05}} | ||
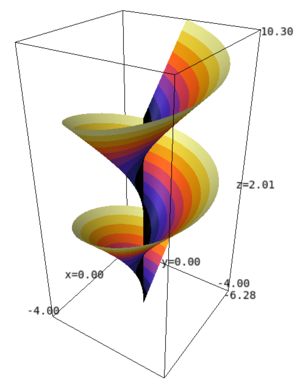
| − | + | A [[Ruled surface|ruled surface]] described by a straight line that rotates at a constant angular rate around a fixed axis, intersects the axis at a constant angle $\alpha$, and at the same time becomes gradually displaced at a constant rate $k$ along this axis. The equation of a helicoid in parametric form is | |
| + | \[ | ||
| + | x = \rho \cos t \quad y = \rho \sin t \quad z = \rho \arctan \alpha + kt\, . | ||
| + | \] | ||
| + | If $\alpha = \pi/2$ the helicoid is called straight or right (cf. Fig. 1), otherwise it is called oblique. However, it is common to use the word "helicoid" without specification for the straight helicoid. Every straight helicoid is a [[Minimal surface|minimal surface]], i.e. it has mean curvature zero. In fact the straight helicoid can be characterized by the property of being the only minimal ruled suface. More precisely we have the following | ||
| − | + | '''Theorem''' | |
| + | If $\Sigma\subset \mathbb R^3$ is a connected $2$-dimensional ruled minimal surface, then it is a subset of a straight helicoid or a subset of a plane. | ||
| − | + | Locally the helicoid is isometric to the [[Catenoid|catenoid]]. In fact such local isometry can be achieved as endpoint of a continuous one-parameter family of isometric deformations which are all minimal surfaces. | |
| − | + | [[File:Helicoide.png|center|300px|Straight helicoid]] | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
====References==== | ====References==== | ||
| − | + | {| | |
| + | |- | ||
| + | |valign="top"|{{Ref|BG}}|| M. Berger, B. Gostiaux, "Differential geometry: manifolds, curves, and surfaces" , Springer (1988) {{MR|0917479}} {{ZBL|0629.53001}} | ||
| + | |- | ||
| + | |valign="top"|{{Ref|Doc}}|| M.P. Do Carmo, "Differential geometry of curves and surfaces" , Prentice-Hall (1975) pp. 214 {{MR|}} {{ZBL|0733.53001}} {{ZBL|0606.53002}} {{ZBL|0326.53001}} | ||
| + | |- | ||
| + | |valign="top"|{{Ref|ON}}|| B. O'Neill, "Elementary differential geometry" , Acad. Press (1966) {{MR|}} {{ZBL|0971.53500}} {{ZBL|0974.53001}} | ||
| + | |- | ||
| + | |valign="top"|{{Ref|Sp}}|| M. Spivak, "A comprehensive introduction to differential geometry" , '''1979''' , Publish or Perish pp. 218–219 {{MR|0532834}} {{MR|0532833}} {{MR|0532832}} {{MR|0532831}} {{MR|0532830}} {{MR|0394453}} {{MR|0394452}} {{MR|0372756}} {{MR|1537051}} {{MR|0271845}} {{MR|0267467}} {{ZBL|1213.53001}} {{ZBL|0439.53005}} {{ZBL|0439.53004}} {{ZBL|0439.53003}} {{ZBL|0439.53002}} {{ZBL|0439.53001}} {{ZBL|0306.53003}} {{ZBL|0306.53002}} {{ZBL|0306.53001}} {{ZBL|0202.52201}} {{ZBL|0202.52001}} | ||
| + | |- | ||
| + | |} | ||
Latest revision as of 19:56, 12 November 2023
2020 Mathematics Subject Classification: Primary: 53A10 Secondary: 49Q05 [MSN][ZBL]
A ruled surface described by a straight line that rotates at a constant angular rate around a fixed axis, intersects the axis at a constant angle $\alpha$, and at the same time becomes gradually displaced at a constant rate $k$ along this axis. The equation of a helicoid in parametric form is \[ x = \rho \cos t \quad y = \rho \sin t \quad z = \rho \arctan \alpha + kt\, . \] If $\alpha = \pi/2$ the helicoid is called straight or right (cf. Fig. 1), otherwise it is called oblique. However, it is common to use the word "helicoid" without specification for the straight helicoid. Every straight helicoid is a minimal surface, i.e. it has mean curvature zero. In fact the straight helicoid can be characterized by the property of being the only minimal ruled suface. More precisely we have the following
Theorem If $\Sigma\subset \mathbb R^3$ is a connected $2$-dimensional ruled minimal surface, then it is a subset of a straight helicoid or a subset of a plane.
Locally the helicoid is isometric to the catenoid. In fact such local isometry can be achieved as endpoint of a continuous one-parameter family of isometric deformations which are all minimal surfaces.
References
| [BG] | M. Berger, B. Gostiaux, "Differential geometry: manifolds, curves, and surfaces" , Springer (1988) MR0917479 Zbl 0629.53001 |
| [Doc] | M.P. Do Carmo, "Differential geometry of curves and surfaces" , Prentice-Hall (1975) pp. 214 Zbl 0733.53001 Zbl 0606.53002 Zbl 0326.53001 |
| [ON] | B. O'Neill, "Elementary differential geometry" , Acad. Press (1966) Zbl 0971.53500 Zbl 0974.53001 |
| [Sp] | M. Spivak, "A comprehensive introduction to differential geometry" , 1979 , Publish or Perish pp. 218–219 MR0532834 MR0532833 MR0532832 MR0532831 MR0532830 MR0394453 MR0394452 MR0372756 MR1537051 MR0271845 MR0267467 Zbl 1213.53001 Zbl 0439.53005 Zbl 0439.53004 Zbl 0439.53003 Zbl 0439.53002 Zbl 0439.53001 Zbl 0306.53003 Zbl 0306.53002 Zbl 0306.53001 Zbl 0202.52201 Zbl 0202.52001 |
Helicoid. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Helicoid&oldid=17660