Tangle move

For given $n$-tangles $T_1$ and $T_2$ (cf. also Tangle), the tangle move, or more specifically the $(T_1,T_2)$-move, is substitution of the tangle $T_2$ in the place of the tangle $T_1$ in a link (or tangle). The simplest tangle $2$-move is a crossing change. This can be generalized to $n$-moves (cf. Montesinos–Nakanishi conjecture or [a5]), $(m,q)$-moves (cf. Fig.a1), and $(p/q)$-rational moves, where a rational $(p/q)$-tangle is substituted in place of the identity tangle [a6] (Fig.a2 illustrates a $(13/5)$-rational move).

A $(p/q)$-rational move preserves the space of Fox $p$-colourings of a link or tangle (cf. Fox $n$-colouring). For a fixed prime number $p$, there is a conjecture that any link can be reduced to a trivial link by $(p/q)$-rational moves ($|q| \le p/2$).

Kirby moves (cf. Kirby calculus) can be interpreted as tangle moves on framed links.

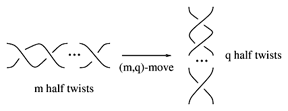
Figure: t130020a

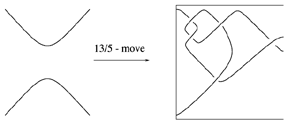
Figure: t130020b

Habiro $C_n$-moves [a2] are prominent in the theory of Vassiliev–Gusarov invariants of links and $3$-manifolds. The simplest and most extensively studied Habiro move (beyond the crossing change) is the $\Delta$-move on a $3$-tangle (cf. Fig.a3). One can reduce every knot into the trivial knot by $\Delta$-moves [a4].

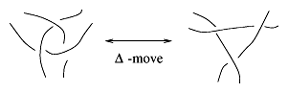
Figure: t130020c

References

[a1]	T. Harikae, Y. Uchida, "Irregular dihedral branched coverings of knots" M. Bozhüyük (ed.) , Topics in Knot Theory , NATO ASI Ser. C , 399 , Kluwer Acad. Publ. (1993) pp. 269–276
[a2]	K. Habiro, "Claspers and finite type invariants of links" Geometry and Topology , 4 (2000) pp. 1–83 Zbl 0941.57015
[a3]	R. Kirby, "Problems in low-dimensional topology" W. Kazez (ed.) , Geometric Topology (Proc. Georgia Internat. Topology Conf., 1993) , Studies in Adv. Math. , 2 , Amer. Math. Soc. /IP (1997) pp. 35–473
[a4]	H. Murakami, Y. Nakanishi, "On a certain move generating link homology" Math. Ann. , 284 (1989) pp. 75–89
[a5]	J.H. Przytycki, "$3$-coloring and other elementary invariants of knots" , Knot Theory , 42 , Banach Center Publ. (1998) pp. 275–295
[a6]	Y. Uchida, S. Suzuki (ed.) , Knots '96, Proc. Fifth Internat. Research Inst. of MSJ , World Sci. (1997) pp. 109–113