Difference between revisions of "Listing knot"
From Encyclopedia of Mathematics
(TeX) |
(svg picture) |
||
| (One intermediate revision by the same user not shown) | |||
| Line 5: | Line 5: | ||
Figure: l059730a | Figure: l059730a | ||
| + | |||
| + | [[File:Listing knot.svg|center|100px|Listing knot projection]] | ||
====References==== | ====References==== | ||
| − | <table><TR><TD valign="top">[1]</TD> <TD valign="top"> | + | <table> |
| − | + | <TR><TD valign="top">[1]</TD> <TD valign="top"> I.B. Listing, "Vorstudien zur Topologie", Göttingen (1847)</TD></TR> | |
| − | + | <TR><TD valign="top">[a1]</TD> <TD valign="top"> R.H. Crowell, R.H. Fox, "Introduction to knot theory", Ginn (1963)</TD></TR> | |
| − | + | <TR><TD valign="top">[a2]</TD> <TD valign="top"> L.H. Kauffman, "On knots", Princeton Univ. Press (1987)</TD></TR> | |
| − | + | </table> | |
| − | + | {{OldImage}} | |
| − | |||
| − | |||
Latest revision as of 18:02, 22 April 2023
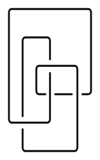
One of the simplest non-trivial knots (see Fig. and Knot theory). A Listing knot is denoted by the symbol $4_1$ (see Knot table) and is sometimes called a figure 8 or fourfold knot. The group of the Listing knot (cf. Knot and link groups) has the presentation $|x,y\colon yx^{-1}yxy^{-1}=x^{-1}yxy^{-1}x|$, and the Alexander polynomial is $\Delta_1=t^2-3t+1$. It was considered by I.B. Listing [1].

Figure: l059730a
References
| [1] | I.B. Listing, "Vorstudien zur Topologie", Göttingen (1847) |
| [a1] | R.H. Crowell, R.H. Fox, "Introduction to knot theory", Ginn (1963) |
| [a2] | L.H. Kauffman, "On knots", Princeton Univ. Press (1987) |
🛠️ This page contains images that should be replaced by better images in the SVG file format. 🛠️
How to Cite This Entry:
Listing knot. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Listing_knot&oldid=31597
Listing knot. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Listing_knot&oldid=31597
This article was adapted from an original article by M.Sh. Farber (originator), which appeared in Encyclopedia of Mathematics - ISBN 1402006098. See original article