Difference between revisions of "Riemann surface"
Ulf Rehmann (talk | contribs) m (MR/ZBL numbers added) |
m (fixing superscripts) |
||
| (3 intermediate revisions by 2 users not shown) | |||
| Line 1: | Line 1: | ||
| − | + | <!-- | |
| + | r0820401.png | ||
| + | $#A+1 = 321 n = 0 | ||
| + | $#C+1 = 321 : ~/encyclopedia/old_files/data/R082/R.0802040 Riemann surface | ||
| + | Automatically converted into TeX, above some diagnostics. | ||
| + | Please remove this comment and the {{TEX|auto}} line below, | ||
| + | if TeX found to be correct. | ||
| + | --> | ||
| − | + | {{TEX|auto}} | |
| + | {{TEX|done}} | ||
| − | + | ''of an analytic function $ w = f( z) $ of a complex variable $ z $'' | |
| − | + | A surface $ R $ | |
| + | such that the [[Complete analytic function|complete analytic function]] $ w = f( z) $, | ||
| + | which is, in general, multiple-valued, can be considered as a single-valued analytic function $ w = F( p) $ | ||
| + | of a point $ p $ | ||
| + | on $ R $. | ||
| − | + | The concept of a Riemann surface arose in connection with the studies of algebraic functions $ w = f( z) $ | |
| + | defined by an algebraic equation | ||
| − | + | $$ \tag{1 } | |
| + | a _ {0} ( z) w ^ {m} + a _ {1} ( z) w ^ {m- 1} + \dots + a _ {m} ( z) = 0, | ||
| + | $$ | ||
| − | + | where $ a _ {j} ( z) $, | |
| + | $ j = 0 \dots m $, | ||
| + | are polynomials with constant coefficients, $ a _ {0} ( z) \neq 0 $, | ||
| + | $ a _ {m} ( z) \neq 0 $. | ||
| + | In the works of V. Puiseux (1850–1851) one discovers a clear understanding of multiple-valuedness, characteristic of these functions $ w = f( z) $, | ||
| + | when to each value of the variable $ z $, | ||
| + | $ m $ | ||
| + | values of the variable $ w $ | ||
| + | correspond. B. Riemann (1851–1857, see [[#References|[1]]]) was the first to show how for any algebraic function one can construct a surface on which this function can be considered as a single-valued rational function of the point. The obtained Riemann surface can be identified with the [[Algebraic curve|algebraic curve]] defined by equation (1). In general, a mutual penetration (sometimes more intensive, sometimes less intensive) of ideas and methods of the theory of functions of a complex variable on the one hand and of algebra and algebraic geometry on the other hand is characteristic of the whole period of further development of the theory of Riemann surfaces, associated with the names of F. Klein, H. Poincaré, P. Koebe, and others. The landmark of this development was the first edition of the book of H. Weyl [[#References|[18]]], in which the general concept of an abstract Riemann surface was formulated. | ||
| − | + | Definition A: A connected topological [[Hausdorff space|Hausdorff space]] $ R $ | |
| + | is called an abstract Riemann surface or, simply, a Riemann surface, if it admits a covering by open sets $ U $ | ||
| + | together with a [[Homeomorphism|homeomorphism]] $ \alpha : U \rightarrow D $ | ||
| + | corresponding to each set $ U $, | ||
| + | where $ D = \{ {z \in \mathbf C } : {| z | < 1 } \} $ | ||
| + | is the unit disc in the complex $ z $-plane $ \mathbf C $; | ||
| + | moreover, if a point $ p \in R $ | ||
| + | belongs to $ U $ | ||
| + | and $ U ^ \prime $, | ||
| + | then the one-to-one correspondence $ z ^ \prime = \alpha ^ \prime \alpha ^ {- 1} ( z) $ | ||
| + | should be a [[Conformal mapping|conformal mapping]] of the first kind in a neighbourhood of the point $ \alpha ( p) \in D $, | ||
| + | that is, $ z ^ \prime = \alpha ^ \prime \alpha ^ {- 1} ( z) $ | ||
| + | is a univalent analytic function in a neighbourhood of the point $ \alpha ( p) \in D $. | ||
| + | In other words, an abstract Riemann surface is a two-dimensional complex-analytic manifold. | ||
| − | + | The definition of a Riemann surface with boundary $ \overline{R} $ | |
| + | differs from definition $ A $ | ||
| + | by the fact that together with the homeomorphisms $ \alpha : U \rightarrow D $, | ||
| + | homeomorphisms $ \alpha : U \rightarrow D _ {0} ^ {+} $ | ||
| + | are admitted, where $ D _ {0} ^ {+} = \{ {z \in \mathbf C } : {| z | < 1, \mathop{\rm Im} z \geq 0 } \} $ | ||
| + | is the unit upper half-disc in $ \mathbf C $; | ||
| + | moreover, it is usually assumed that $ \overline{R} $ | ||
| + | is not already a Riemann surface in the sense of definition $ A $. | ||
| + | The points of a Riemann surface with boundary $ \overline{R} $ | ||
| + | that have neighbourhoods homeomorphic to $ D $ | ||
| + | are called interior and the other points, that are mapped to the points of the segment | ||
| − | + | $$ | |
| + | \{ {z = x + iy \in \mathbf C } : {- 1 < x < 1, y = 0 } \} | ||
| + | , | ||
| + | $$ | ||
| − | + | form the boundary $ \partial \overline{R} $. | |
| + | The set of interior points of $ \overline{R} $ (the interior of $ \overline{R} $) | ||
| + | is a Riemann surface in the sense of definition $ A $. | ||
| + | Thus, in the case of a Riemann surface with boundary, the boundary is usually considered to be a non-empty set. | ||
| − | + | A Riemann surface (with boundary) is a triangulable and orientable manifold with a countable base and, hence, it is separable and metrizable. A compact Riemann surface (without boundary) is called a closed Riemann surface; the wider class of finite Riemann surfaces includes the closed Riemann surfaces and the compact Riemann surfaces with a boundary consisting of a finite number of connected components. Non-compact Riemann surfaces with boundary or without it are called open Riemann surfaces. In certain cases it is more convenient to admit in definition $ A $ | |
| + | not only conformal mappings of the first kind but also conformal mappings of the second kind. A Riemann surface with boundary $ \overline{R}\; $( | ||
| + | or without it) obtained using such an approach is, generally speaking, not orientable any more, but under the assumption that it be finite it can be conformally imbedded in an orientable closed Riemann surface: the double of $ \overline{R} $ (see [[#References|[8]]], cf. [[Double of a Riemann surface|Double of a Riemann surface]]). | ||
| − | + | Let an analytic function $ w = f( z) $ | |
| + | be given by one of its regular elements $ ( a, P) = ( a, P( z- a)) $, | ||
| + | i.e. by a pair consisting of a point $ a \in \mathbf C $ | ||
| + | and a power series | ||
| − | + | $$ | |
| + | P( z- a) = \sum _ {\nu = 0 } ^ \infty a _ \nu ( z- a) ^ \nu | ||
| + | $$ | ||
| − | + | with centre $ a $ | |
| + | and radius of convergence $ r( a) $, | ||
| + | $ 0 < r( a) \leq \infty $. | ||
| + | [[Analytic continuation|Analytic continuation]] of the element $ ( a, P) $ | ||
| + | along all possible paths in the extended plane $ \overline{\mathbf C} $ | ||
| + | allows one to obtain all regular elements $ ( b, Q) $ | ||
| + | of the same type; in their totality they form the complete analytic function, which is also denoted by $ w = f( z) $. | ||
| + | Moreover, under analytic continuation elements of a more general nature arise: | ||
| − | + | $$ | |
| + | ( b, S) = ( b, S(( z- b) ^ {1/n} )), | ||
| + | $$ | ||
| − | + | i.e. pairs consisting of a point $ b \in \overline{\mathbf C} $ | |
| + | and a generalized power series (a Puiseux series): | ||
| − | + | $$ | |
| + | S(( z- b) ^ {1/n} ) = \sum _ {\nu = m } ^ \infty b _ {n} ( z- b) ^ {\nu /n } | ||
| + | $$ | ||
| − | + | or (in the case when $ b = \infty $ | |
| + | is the point at infinity): | ||
| − | + | $$ | |
| + | S( z ^ {- 1/n} ) = \sum _ {\nu = m } ^ \infty b _ \nu z ^ {- \nu /n } , | ||
| + | $$ | ||
| − | where < | + | where $ m $ |
| + | is an integer and $ n $ | ||
| + | is a positive integer. Moreover, these series converge when $ | z- b | < r( b) $ | ||
| + | or $ | z | > r( \infty ) > 0 $, | ||
| + | respectively. The generalized elements $ ( b, S) $ | ||
| + | or, more precisely, their equivalence classes, form in their totality the [[Analytic image|analytic image]] $ A _ {f} $ | ||
| + | corresponding to the given analytic function $ w = f( z) $. | ||
| + | Among the equivalence classes of elements $ ( b, S) $ | ||
| + | that form the analytic image one can distinguish regular ones, when $ n= 1 $, | ||
| + | and ramified ones, when $ n> 1 $. | ||
| + | The introduction of an appropriate topology on the analytic image $ A _ {f} $ | ||
| + | will turn it into the Riemann surface $ R _ {f} $ | ||
| + | of the analytic function $ w = f( z) $. | ||
| + | This can be achieved, for example, by defining the neighbourhood of an element $ ( b, S) $, | ||
| + | $ b \neq \infty $, | ||
| + | as the set consisting of the element $ ( b, S) $ | ||
| + | itself and all the regular elements $ ( a, P) $ | ||
| + | of $ A _ {f} $ | ||
| + | for which $ | b- a | < \rho ^ {n} $, | ||
| + | $ \rho < r( b) $, | ||
| + | and the series $ P( z- a) $ | ||
| + | converges to one of the $ n $ | ||
| + | determinations of the series $ S(( z- b) ^ {1/n} ) $ | ||
| + | in their common domain of definition, i.e. | ||
| − | + | $$ | |
| + | P( z- a) \equiv S( \epsilon ( z- b) ^ {1/n} ), | ||
| + | $$ | ||
| − | + | where $ \epsilon $ | |
| + | is one of the $ n $-th order roots of unity, $ \epsilon ^ {n} = 1 $. | ||
| + | The neighbourhood of the element $ ( \infty , S) $ | ||
| + | consists of the element $ ( \infty , S) $ | ||
| + | itself and all those regular elements $ ( a, P) $ | ||
| + | of $ A _ {f} $ | ||
| + | for which $ | a | > \rho ^ {- 1} $, | ||
| + | $ \rho < r( b) $, | ||
| + | and the series $ P( z- a) $ | ||
| + | converges to one of the $ n $ | ||
| + | determinations of the series $ S( z ^ {- 1/n} ) $. | ||
| + | The space $ R _ {f} $ | ||
| + | satisfies all the conditions of definition $ A $. | ||
| − | + | Thus, to any analytic function $ w = f( z) $ | |
| + | corresponds a Riemann surface $ R _ {f} $ | ||
| + | on which this function is a single-valued analytic function $ w = F( p) $ | ||
| + | of a point $ p = ( b, S) \in R _ {f} $. | ||
| + | This means that in a neighbourhood of any point $ p _ {0} = ( b, S) $ | ||
| + | there exists a [[Local uniformizing parameter|local uniformizing parameter]] $ t = ( z- b) ^ {1/n} $ | ||
| + | in which $ w $ | ||
| + | is represented as a single-valued analytic function $ w = P( t) = F( p) $. | ||
| + | In other words, the Riemann surface $ R _ {f} $ | ||
| + | of an analytic function is a geometric construct that is used for the global [[Uniformization|uniformization]] of a, generally speaking, multiple-valued relation $ w = f( z) $. | ||
| + | In a neighbourhood of each point $ p _ {0} = ( b, S) \in R _ {f} $ | ||
| + | this relation is uniformized by the two single-valued analytic functions $ z = b+ t ^ {n} $ | ||
| + | and $ w = S( t) $. | ||
| + | On the other hand, the projection $ \pi : ( b, S) \rightarrow b $ | ||
| + | that takes each element $ p _ {0} = ( b, S) \in R _ {f} $ | ||
| + | to its centre $ b $ | ||
| + | shows that the Riemann surface $ R _ {f} $ | ||
| + | of an analytic function is a (ramified) [[Covering surface|covering surface]] over the extended complex plane $ \overline{\mathbf C}\; $ | ||
| + | or, which is the same, over the [[Riemann sphere|Riemann sphere]]. The projections of the ramified elements $ ( b, S) $ | ||
| + | with $ n > 1 $ | ||
| + | are branch points of this covering. | ||
| + | |||
| + | At the same time, to each a priori given Riemann surface $ R $ | ||
| + | correspond infinitely-many analytic functions $ w = f( z) $ | ||
| + | with precisely $ R $ | ||
| + | as Riemann surface, $ R _ {f} = R $. | ||
| + | For the case of closed Riemann surfaces this statement was formulated and proved already by Riemann in 1851. The central point of the corresponding proof is the construction on $ R $ | ||
| + | of harmonic functions with given singularities. The proof given by Riemann was based on an uncritical application of the so-called [[Dirichlet principle|Dirichlet principle]]; Koebe (1909) was the first to give a rigorous proof; later there appeared simpler proofs of this fundamental statement, among them those based on the properly applied Dirichlet principle (see, e.g. [[#References|[3]]], [[#References|[4]]], [[#References|[17]]], [[#References|[18]]]). | ||
| + | |||
| + | Whatever the orientable topological surface $ S $ | ||
| + | may be, one can construct a Riemann surface $ R $ | ||
| + | homeomorphic to $ S $, | ||
| + | i.e. a Riemann surface of the same topological type as $ S $. | ||
| + | Closed Riemann surfaces are topologically completely determined by one number — the genus $ g $, | ||
| + | $ 0 \leq g < + \infty $( | ||
| + | cf. [[Genus of a surface|Genus of a surface]]). The topological type of such a Riemann surface $ R $ | ||
| + | for $ g = 0 $ | ||
| + | is a sphere, for $ g = 1 $— | ||
| + | a torus, for $ g > 1 $— | ||
| + | a generalized torus, or a sphere with $ g $ | ||
| + | handles. By cutting a Riemann surface $ R $ | ||
| + | of genus $ g = 0 $ | ||
| + | along some arc one obtains a digon with the symbol $ s = aa ^ {- 1} $ | ||
| + | as its topological model or normal form, indicating that the points of the sides $ a $ | ||
| + | and $ a ^ {- 1} $ | ||
| + | are identified; when $ g \geq 1 $ | ||
| + | one has to carry out $ 2g $ [[Canonical sections|canonical sections]] $ a _ {1} , b _ {1} \dots a _ {g} , b _ {g} $, | ||
| + | after which one obtains the normal form of a closed Riemann surface $ R $— | ||
| + | a polygon with $ 4g $ | ||
| + | pairwise-identified sides; the symbol $ s = a _ {1} \dots $ | ||
| + | should indicate the order of appearance of the sides. For instance, in Fig. athe normal forms of a sphere for $ g= 0 $ | ||
| + | and a torus for $ g= 1 $ | ||
| + | are shown together with their symbols. | ||
<img style="border:1px solid;" src="https://www.encyclopediaofmath.org/legacyimages/common_img/r082040a.gif" /> | <img style="border:1px solid;" src="https://www.encyclopediaofmath.org/legacyimages/common_img/r082040a.gif" /> | ||
| Line 51: | Line 214: | ||
Figure: r082040a | Figure: r082040a | ||
| − | From the analytic point of view a closed Riemann surface | + | From the analytic point of view a closed Riemann surface $ R $ |
| + | is characterized by the fact that it is the Riemann surface of some algebraic function $ w = f( z) $ | ||
| + | defined by an algebraic equation (1) of degree $ m $. | ||
| + | This Riemann surface $ R $ | ||
| + | can be imagined as $ m $ | ||
| + | sheets extending over the Riemann sphere and mutually connected in a certain manner at the branch points and along some lines connecting these points (the manner of connecting is determined by the specific form of equation (1)). The genus $ g $ | ||
| + | of the Riemann surface $ R $ | ||
| + | can in this case be expressed as a function of the number of sheets $ m $ | ||
| + | and the orders $ k _ {1} \dots k _ {s} $ | ||
| + | of the branch points by the [[Riemann–Hurwitz formula|Riemann–Hurwitz formula]] | ||
| − | + | $$ | |
| + | g = \sum _ {\nu = 1 } ^ { s } | ||
| + | \frac{k _ \nu - 1 }{2} | ||
| + | - m + 1. | ||
| + | $$ | ||
| − | Finite Riemann surfaces | + | Finite Riemann surfaces $ \overline{R}\; $ |
| + | are topologically completely characterized by the genus $ g $, | ||
| + | $ 0 \leq g < \infty $, | ||
| + | and the number $ l $ | ||
| + | of connected components of the boundary; their topological type is a sphere with $ g $ | ||
| + | handles and $ l $ | ||
| + | holes. In the normal form of a finite Riemann surface, the number of sides is not necessarily even, some sides corresponding to components of the boundary that remain free are not identified. The notion of the genus can also be generalized to open Riemann surfaces $ R $, | ||
| + | for example by exhausting $ R $ | ||
| + | by a sequence $ \{ \overline{R} _ \nu \} _ {\nu = 1 } ^ \infty $ | ||
| + | of compact Riemann surfaces with boundary $ \overline{R} _ \nu $, | ||
| + | belonging to $ R $, | ||
| + | and such that $ \overline{R} _ \nu $ | ||
| + | is contained in $ \overline{R} _ {\nu + 1 } $, | ||
| + | $ \cup _ {\nu = 1 } ^ \infty \overline{R} _ \nu = R $. | ||
| + | The genus $ g $ | ||
| + | of $ R $ | ||
| + | is set equal to $ g = \lim\limits _ {\nu \rightarrow \infty } g _ \nu $, | ||
| + | where $ g _ \nu $ | ||
| + | is the genus of $ \overline{R} _ \nu $. | ||
| + | This limit exists and is independent of the choice of the exhaustion $ \{ \overline{R} _ \nu \} $, | ||
| + | $ 0 \leq g \leq + \infty $. | ||
| + | However, the genus does not completely define the topological type of an open Riemann surface; the topological types of open Riemann surfaces can be rather diverse. Thus, in Fig.2a, Fig.2b two models with $ g= 0 $ | ||
| + | and $ g= 2 $, | ||
| + | respectively, are shown. | ||
| − | An important topological characteristic of a Riemann surface | + | An important topological characteristic of a Riemann surface $ R $ |
| + | is the order of connectivity: $ R $ | ||
| + | is called simply connected if any simple closed curve in $ R $ | ||
| + | can be deformed continuously into a point without getting out of $ R $, | ||
| + | i.e. in other words, if the [[Fundamental group|fundamental group]] of $ R $ | ||
| + | is trivial. Otherwise the Riemann surface $ R $ | ||
| + | is called multiply connected. The schlichtartig Riemann surfaces form an important class of Riemann surfaces; they are the Riemann surfaces (with boundary or without) that are split by any simple closed curve into non-intersecting parts. For example, in Fig.2a a topological model of a multiply-connected schlichtartig Riemann surface is shown. A schlichtartig Riemann surface necessarily has genus zero. A schlichtartig Riemann surface $ R $ | ||
| + | is called $ n $-connected if the minimum number of sections necessary to convert $ R $ | ||
| + | to a simply-connected Riemann surface is equal to $ n- 1 $, | ||
| + | $ n \geq 1 $ (see Fig.2b). | ||
<img style="border:1px solid;" src="https://www.encyclopediaofmath.org/legacyimages/common_img/r082040b.gif" /> | <img style="border:1px solid;" src="https://www.encyclopediaofmath.org/legacyimages/common_img/r082040b.gif" /> | ||
| Line 67: | Line 275: | ||
Figure: r082040c | Figure: r082040c | ||
| − | The topological properties of a Riemann surface | + | The topological properties of a Riemann surface $ R $ |
| + | do not completely characterize the analytic properties of $ R $, | ||
| + | i.e. the topological properties of $ R $ | ||
| + | do not completely characterize the behaviour of functions of different classes on $ R $. | ||
| + | In particular, let $ f: R _ {1} \rightarrow R _ {2} $ | ||
| + | be a function on the Riemann surface $ R _ {1} $ | ||
| + | with values on another Riemann surface $ R _ {2} $. | ||
| + | The function $ f $ | ||
| + | is called analytic on $ R _ {1} $ | ||
| + | if for any point $ p _ {0} \in R _ {1} $, | ||
| + | $ f( p _ {0} ) = q _ {0} $, | ||
| + | one can find local uniformizing parameters $ t = \phi ( p) $ | ||
| + | in a neighbourhood of $ p _ {0} $ | ||
| + | on $ R _ {1} $ | ||
| + | and $ \tau = \psi ( q) $ | ||
| + | in a neighbourhood of $ q _ {0} $ | ||
| + | on $ R _ {2} $, | ||
| + | respectively, such that the composite function | ||
| − | + | $$ | |
| + | \tau = \psi \{ f[ \phi ^ {- 1} ( t)] \} = g( t) | ||
| + | $$ | ||
| − | is an analytic function of the complex variable | + | is an analytic function of the complex variable $ t $ |
| + | in a neighbourhood of the value $ t _ {0} = \phi ( p _ {0} ) $. | ||
| + | Two Riemann surfaces $ R _ {1} $ | ||
| + | and $ R _ {2} $ | ||
| + | are called conformally equivalent, or are said to belong to the same conformal class (cf. [[Riemann surfaces, conformal classes of|Riemann surfaces, conformal classes of]]), if there exists an analytic function $ f: R _ {1} \rightarrow R _ {2} $ | ||
| + | that gives a one-to-one mapping from $ R _ {1} $ | ||
| + | onto $ R _ {2} $. | ||
| + | From the point of view of the behaviour of analytic functions on Riemann surfaces, conformally-equivalent Riemann surfaces are considered as one and the same Riemann surface, but topologically-equivalent Riemann surfaces are not always conformally equivalent. | ||
| − | In terms of Riemann surfaces, the Riemann mapping theorem can be formulated as follows: Any simply-connected Riemann surface is conformally equivalent to one of the following three domains: 1) the extended complex plane | + | In terms of Riemann surfaces, the Riemann mapping theorem can be formulated as follows: Any simply-connected Riemann surface is conformally equivalent to one of the following three domains: 1) the extended complex plane $ \overline{\mathbf C} = \mathbf C \cup \{ \infty \} $, |
| + | i.e. the Riemann sphere (the elliptic case); 2) the finite complex plane $ \mathbf C $, | ||
| + | i.e. the punctured Riemann sphere (the parabolic case); or 3) the unit disc $ D = \{ {z \in \mathbf C } : {| z | < 1 } \} $ | ||
| + | in $ \mathbf C $, | ||
| + | i.e. the Riemann sphere with a section of positive length (the hyperbolic case). An important result is that any schlichtartig Riemann surface is conformally equivalent to some canonical domain in the extended complex plane. As such a canonical domain one may take the entire extended plane with a finite or infinite number of sections parallel to the real axis; moreover, some of these sections may degenerate into points. As mentioned above, in the case of a simply-connected Riemann surface the canonical domain either has no sections (elliptic type), or the section degenerates into a point (parabolic type), or the section has a positive length (hyperbolic type). All three types of simply-connected Riemann surfaces are conformally different, although the last two of them are topologically equivalent. The problem of types, which has not yet (1991) been solved completely, consists in finding additional conditions under which a simply-connected Riemann surface will be of hyperbolic or parabolic type (see [[#References|[6]]], [[#References|[7]]], [[#References|[10]]], [[#References|[11]]], and [[Riemann surfaces, classification of|Riemann surfaces, classification of]]). | ||
| − | In the case of an arbitrary Riemann surface | + | In the case of an arbitrary Riemann surface $ R $, |
| + | its [[Universal covering|universal covering]] surface $ \widehat{R} $ | ||
| + | will always be a simply-connected Riemann surface, and thus belongs to one of the three types above. The Riemann surface $ R $ | ||
| + | itself is considered to be of elliptic, parabolic or hyperbolic type, according to the type of its universal covering $ \widehat{R} $. | ||
| + | This classification of Riemann surfaces is justified by the following considerations. Let $ D $ | ||
| + | be one of three domains: the extended complex plane, the finite complex plane or the open unit disc, and let $ \Lambda $ | ||
| + | be some group of Möbius transformations of $ D $ | ||
| + | onto itself (automorphisms) without fixed points in $ D $. | ||
| + | A conformal mapping $ w = W( q) $ | ||
| + | of the universal covering $ \widehat{R} $ | ||
| + | onto $ D $ | ||
| + | carries the group $ \widehat \Lambda $ | ||
| + | of transformations of the covering $ \widehat{R} $, | ||
| + | which is isomorphic to the fundamental group $ \pi _ {1} ( R) $, | ||
| + | onto some group $ \Lambda $ | ||
| + | of automorphisms of $ D $. | ||
| + | Moreover, $ w = W( q) $ | ||
| + | can be considered as a conformal mapping from the quotient space $ \widehat{R} / \widehat \Lambda $ | ||
| + | onto the quotient space $ D/ \Lambda $, | ||
| + | and $ \widehat{R} / \widehat \Lambda $ | ||
| + | can be identified with $ R $. | ||
| + | Thus, $ w = W( q) $ | ||
| + | can be considered as a conformal mapping from the Riemann surface $ R $ | ||
| + | onto the quotient space $ D/ \Lambda $ | ||
| + | with some group of automorphisms $ \Lambda $ | ||
| + | isomorphic to the fundamental group $ \pi _ {1} ( R) $. | ||
| − | Since a Riemann surface | + | Since a Riemann surface $ R $ |
| + | of elliptic type is necessarily simply-connected, the group $ \Lambda $ | ||
| + | is trivial and thus such a Riemann surface is necessarily the Riemann surface of the function inverse to a rational function. A simply-connected Riemann surface of parabolic type is necessarily the Riemann surface of the function inverse to a meromorphic function in the finite plane. A compact Riemann surface of genus $ g= 0 $, | ||
| + | $ g= 1 $ | ||
| + | or $ g > 1 $ | ||
| + | is a Riemann surface of elliptic, parabolic or hyperbolic type, respectively. | ||
| − | In connection with the conformal equivalence of Riemann surfaces there arises the question of the structure of the group | + | In connection with the conformal equivalence of Riemann surfaces there arises the question of the structure of the group $ \Sigma $ |
| + | of conformal automorphisms of a Riemann surface $ R $. | ||
| + | Except for certain simple cases, this group $ \Sigma $ | ||
| + | is discrete and for compact Riemann surfaces of genus $ g > 1 $ | ||
| + | it is finite (Schwarz' theorem). There are only seven exceptional cases in which the group $ \Sigma $ | ||
| + | is continuous, namely (representatives of the corresponding conformal classes are given): the sphere in the elliptic case; the sphere with one or two punctures and the torus in the parabolic case; the open disc, the punctured open disc and an annulus in the hyperbolic case. | ||
| − | Of great importance also is the moduli problem for Riemann surfaces in its different versions (cf. [[Moduli of a Riemann surface|Moduli of a Riemann surface]]; [[Moduli problem|Moduli problem]]). It is the problem of the possible description of the diversity of conformally-inequivalent Riemann surfaces of different types. For example, it is easy to establish the following facts. The set of types of conformally-inequivalent doubly-connected schlichtartig Riemann surfaces (annuli) depends on one real parameter (the modulus) < | + | Of great importance also is the moduli problem for Riemann surfaces in its different versions (cf. [[Moduli of a Riemann surface|Moduli of a Riemann surface]]; [[Moduli problem|Moduli problem]]). It is the problem of the possible description of the diversity of conformally-inequivalent Riemann surfaces of different types. For example, it is easy to establish the following facts. The set of types of conformally-inequivalent doubly-connected schlichtartig Riemann surfaces (annuli) depends on one real parameter (the modulus) $ k $, |
| + | $ 0 < k < 1 $; | ||
| + | i.e. two annuli $ 0 < r _ \nu < | z | < R _ \nu $, | ||
| + | $ \nu = 1, 2 $, | ||
| + | are conformally equivalent if and only if the ratios of their radii $ k = ( r _ {1} /R _ {1} ) = ( r _ {2} / R _ {2} ) $ | ||
| + | coincide. The set of types of conformally-inequivalent $ n $-connected schlichtartig Riemann surfaces for $ n > 2 $ | ||
| + | depends on $ 3n- 6 $ | ||
| + | real parameters. The set of types of conformally-inequivalent closed Riemann surfaces of genus $ g \geq 1 $ | ||
| + | for $ g= 1 $ | ||
| + | depends on two real parameters and for $ g > 1 $ | ||
| + | on $ 6g- 6 $ | ||
| + | real parameters (see [[Riemann surfaces, conformal classes of|Riemann surfaces, conformal classes of]], and also [[#References|[3]]], [[#References|[12]]], [[#References|[13]]], , ; concerning the behaviour of functions of other classes on Riemann surfaces see [[Riemann surfaces, classification of|Riemann surfaces, classification of]]). | ||
An important aspect of the theory of Riemann surfaces is its connection with the concept of uniformization. In general, for a multiple-valued analytic function | An important aspect of the theory of Riemann surfaces is its connection with the concept of uniformization. In general, for a multiple-valued analytic function | ||
| − | + | $$ \tag{2 } | |
| + | w = f( z), | ||
| + | $$ | ||
| − | its Riemann surface | + | its Riemann surface $ R _ {f} $ |
| + | provides a geometrical means of uniformization: The multiple-valued relation (2) is replaced by two single-valued relations | ||
| − | + | $$ \tag{3 } | |
| + | w = F( p),\ \ | ||
| + | z = g( p),\ \ | ||
| + | p \in R _ {f} , | ||
| + | $$ | ||
| − | which give a single-valued expression of | + | which give a single-valued expression of $ z $ |
| + | and $ w $ | ||
| + | in the entire domain of definition of the function (2) as a complete analytic function. On the other hand, the approach of K. Weierstrass to the construction of the notion of the complete analytic function of (2) is based on the use of a local uniformizing parameter $ t $ | ||
| + | that allows one to express the variables $ z $ | ||
| + | and $ w $ | ||
| + | analytically as single-valued analytic functions $ z = z( t) $ | ||
| + | and $ w = w( t) $, | ||
| + | locally in a neighbourhood of some point $ ( z _ {0} , w _ {0} ) $, | ||
| + | $ w _ {0} = f( z _ {0} ) $. | ||
| + | The uniformization problem in its simplest classical form is the problem of synthesis of these two ideas. One has to replace the relation (2) in its entire domain of definition by two analytic representations $ z = z( t) $, | ||
| + | $ w = w( t) $, | ||
| + | where $ t $ | ||
| + | is a uniformizing complex variable with values in some domain of the plane. | ||
| − | The above-mentioned statement of the possibility of uniformization was established by Koebe and, independently, by Poincaré almost simultaneously in 1907. If the Riemann surface | + | The above-mentioned statement of the possibility of uniformization was established by Koebe and, independently, by Poincaré almost simultaneously in 1907. If the Riemann surface $ R _ {f} $ |
| + | of the function (2) is simply connected or schlichtartig, then the uniformization problem is reduced to constructing a conformal mapping $ \phi : R _ {f} \rightarrow D $ | ||
| + | from $ R _ {f} $ | ||
| + | onto the planar domain $ D $. | ||
| + | The representations (3) then provide the sought uniformization: | ||
| − | + | $$ | |
| + | z = g[ \phi ^ {- 1} ( t)],\ \ | ||
| + | w = F[ \phi ^ {- 1} ( t)],\ \ | ||
| + | t \in D. | ||
| + | $$ | ||
| − | A conformal mapping | + | A conformal mapping $ f $ |
| + | onto a planar domain exists only for the schlichtartig Riemann surfaces $ R _ {f} $ (the general uniformization theorem). | ||
| − | In the general case of an arbitrary analytic relation (2), the Riemann surface | + | In the general case of an arbitrary analytic relation (2), the Riemann surface $ R _ {f} $ |
| + | is not schlichtartig but its universal covering surface $ \widehat{R} _ {f} $ | ||
| + | is simply connected and, hence, there exists a conformal mapping | ||
| − | + | $$ | |
| + | \psi : \widehat{R} _ {f} \rightarrow D, | ||
| + | $$ | ||
| − | where | + | where $ D $ |
| + | is one of the already-mentioned domains: $ \overline{\mathbf C} $, | ||
| + | $ \mathbf C $ | ||
| + | or the open unit disc. The function $ w = f( z) $ | ||
| + | is meromorphic on the Riemann surface $ \widehat{R} _ {f} $ | ||
| + | and, hence, it is also meromorphic on $ R _ {f} $; | ||
| + | moreover, it depends only on the projection $ p = p( q) $, | ||
| + | $ p \in R _ {f} $, | ||
| + | of a point $ q \in \widehat{R} _ {f} $. | ||
| + | Thus one obtains a geometrical uniformization in the form | ||
| − | + | $$ | |
| + | z = g[ p( q)],\ \ | ||
| + | w = F[ p( q)], | ||
| + | $$ | ||
and from it the analytic uniformization | and from it the analytic uniformization | ||
| − | + | $$ | |
| + | z = g \{ p[ \psi ^ {- 1} ( t) ] \} = \Psi ( t), | ||
| + | $$ | ||
| − | + | $$ | |
| + | w = F \{ p[ \psi ^ {- 1} ( t) ] \} = \Phi ( t),\ t \in D, | ||
| + | $$ | ||
| − | where | + | where $ z $ |
| + | and $ w $ | ||
| + | are expressed as meromorphic functions $ \Phi ( t) $ | ||
| + | and $ \Psi ( t) $ | ||
| + | of a variable $ t \in D $. | ||
| + | These functions $ \Phi ( t) $ | ||
| + | and $ \Psi ( t) $ | ||
| + | are automorphic functions (cf. [[Automorphic function|Automorphic function]]) in $ D $ | ||
| + | relative to the group of automorphisms $ \Lambda $ | ||
| + | isomorphic to the fundamental group $ \pi _ {1} ( R _ {f} ) $ | ||
| + | of the Riemann surface $ R _ {f} $ | ||
| + | of the uniformizing function (see [[#References|[3]]], [[#References|[7]]], , ). | ||
====References==== | ====References==== | ||
<table><TR><TD valign="top">[1]</TD> <TD valign="top"> B. Riemann, "Collected works" , Dover, reprint (1953) {{MR|}} {{ZBL|0703.01020}} {{ZBL|08.0231.03}} </TD></TR><TR><TD valign="top">[2]</TD> <TD valign="top"> A.I. Markushevich, "Theory of functions of a complex variable" , '''1–2''' , Chelsea (1977) (Translated from Russian) {{MR|0444912}} {{ZBL|0357.30002}} </TD></TR><TR><TD valign="top">[3]</TD> <TD valign="top"> A. Hurwitz, R. Courant, "Vorlesungen über allgemeine Funktionentheorie und elliptische Funktionen" , Springer (1964) {{MR|0173749}} {{ZBL|0135.12101}} </TD></TR><TR><TD valign="top">[4]</TD> <TD valign="top"> S. Stoilov, "The theory of functions of a complex variable" , '''1–2''' , Moscow (1962) (In Russian; translated from Rumanian)</TD></TR><TR><TD valign="top">[5]</TD> <TD valign="top"> S. [S. Stoilov] Stoilow, "Leçons sur les principes topologiques de la théorie des fonctions analytiques" , Gauthier-Villars (1938) {{MR|0082545}} {{ZBL|0121.06103}} {{ZBL|0072.07604}} {{ZBL|0017.37802}} </TD></TR><TR><TD valign="top">[6]</TD> <TD valign="top"> G. Springer, "Introduction to Riemann surfaces" , Chelsea, reprint (1981) {{MR|0122987}} {{MR|1530201}} {{MR|0092855}} {{ZBL|0501.30039}} </TD></TR><TR><TD valign="top">[7]</TD> <TD valign="top"> R. Nevanlinna, "Uniformisierung" , Springer (1967) {{MR|0228671}} {{ZBL|0152.27401}} </TD></TR><TR><TD valign="top">[8]</TD> <TD valign="top"> M. Schiffer, D.C. Spencer, "Functionals of finite Riemann surfaces" , Princeton Univ. Press (1954) {{MR|0065652}} {{ZBL|0059.06901}} </TD></TR><TR><TD valign="top">[9]</TD> <TD valign="top"> N.G. Chebotarev, "The theory of algebraic functions" , Moscow-Leningrad (1948) (In Russian)</TD></TR><TR><TD valign="top">[10]</TD> <TD valign="top"> L.I. Volkovyskii, "Investigation of the type problem for a simply-connected Riemann surface" ''Trudy Mat. Inst. Steklov.'' , '''34''' (1950) pp. 3–171 (In Russian) {{MR|0049330}} {{ZBL|}} </TD></TR><TR><TD valign="top">[11]</TD> <TD valign="top"> L.I. Volkovyskii, "Contempory studies on Riemann surfaces" ''Uspekhi Mat. Nauk'' , '''11''' : 5 (1956) pp. 77–84 (In Russian)</TD></TR><TR><TD valign="top">[12]</TD> <TD valign="top"> S.L. Krushkal', "Quasi-conformal mappings and Riemann surfaces" , Winston & Wiley (1979) (Translated from Russian) {{MR|536488}} {{ZBL|}} </TD></TR><TR><TD valign="top">[13]</TD> <TD valign="top"> S.L. Krushkal', B.N. Apanasov, N.A. Gusevskii, "Kleinian groups and uniformization in examples and problems" , Amer. Math. Soc. (1986) (Translated from Russian) {{MR|0835439}} {{ZBL|0579.30001}} </TD></TR><TR><TD valign="top">[14]</TD> <TD valign="top"> E.B. Vinberg, O.V. Shvartsman, "Riemann surfaces" ''J. Soviet Math.'' , '''14''' : 1 (1980) pp. 985–1020 ''Itogi Nauk. i Tekhn. Algebra. Topol. Geom.'' , '''16''' (1978) pp. 191–245 {{MR|0538254}} {{ZBL|0445.30032}} </TD></TR><TR><TD valign="top">[15a]</TD> <TD valign="top"> L. Bers, "Quasi-conformal mappings and Teichmüller's theorem" R. Nevanlinna (ed.) et al. (ed.) , ''Analytic functions'' , Princeton Univ. Press (1960) pp. 89–119 {{MR|114898}} {{ZBL|}} </TD></TR><TR><TD valign="top">[15b]</TD> <TD valign="top"> L.V. Ahlfors, "The complex analytic structure of the space of closed Riemann surfaces" R. Nevanlinna (ed.) et al. (ed.) , ''Analytic functions'' , Princeton Univ. Press (1960) pp. 45–66 {{MR|0124486}} {{ZBL|0100.28903}} </TD></TR><TR><TD valign="top">[15c]</TD> <TD valign="top"> L. Bers, "Spaces of Riemann surfaces" J.A. Todd (ed.) , ''Proc. Internat. Congress Mathematicians (Edinburgh, 1958)'' , Cambridge Univ. Press (1960) pp. 349–361 {{MR|0124484}} {{MR|0111835}} {{ZBL|0116.28803}} {{ZBL|0106.28501}} </TD></TR><TR><TD valign="top">[15d]</TD> <TD valign="top"> L. Bers, "Simultaneous uniformization" ''Bull. Amer. Math. Soc.'' , '''66''' (1960) pp. 94–97 {{MR|0111834}} {{ZBL|0090.05101}} </TD></TR><TR><TD valign="top">[15e]</TD> <TD valign="top"> L. Bers, "Holomorphic differentials as functions of moduli" ''Bull. Amer. Math. Soc.'' , '''67''' (1961) pp. 206–210 {{MR|0122989}} {{ZBL|0102.06702}} </TD></TR><TR><TD valign="top">[15f]</TD> <TD valign="top"> L. Ahlfors, "On quasiconformal mappings" ''J. d'Anal. Math.'' , '''3''' (1954) pp. 1–58; 207–208 {{MR|0064875}} {{ZBL|0057.06506}} </TD></TR><TR><TD valign="top">[16a]</TD> <TD valign="top"> L. Bers, "Uniformization, moduli, and Kleinian groups" ''Bull. London Math. Soc.'' , '''4''' (1972) pp. 257–300 {{MR|0348097}} {{ZBL|0257.32012}} </TD></TR><TR><TD valign="top">[16b]</TD> <TD valign="top"> L. Bers, "The moduli of Kleinian groups" ''Russian Math. Surveys'' , '''29''' : 2 (1974) pp. 88–102 ''Uspekhi Mat. Nauk'' , '''29''' : 2 (1974) pp. 86–102 {{MR|0422691}} {{ZBL|}} </TD></TR><TR><TD valign="top">[17]</TD> <TD valign="top"> F. Klein, "Riemannschen Flächen" , Springer, reprint (1986)</TD></TR><TR><TD valign="top">[18]</TD> <TD valign="top"> H. Weyl, "The concept of a Riemann surface" , Addison-Wesley (1955) (Translated from German) {{MR|1440406}} {{MR|0166351}} {{ZBL|}} </TD></TR><TR><TD valign="top">[19]</TD> <TD valign="top"> L.V. Ahlfors, L. Sario, "Riemann surfaces" , Princeton Univ. Press (1974) {{MR|0667739}} {{MR|0712145}} {{MR|0279300}} {{MR|0204641}} {{MR|0130368}} {{MR|0124486}} {{MR|0114911}} {{MR|0093583}} {{MR|0083561}} {{MR|1565732}} {{MR|0090649}} {{MR|0055250}} {{MR|0054729}} {{MR|0054055}} {{MR|0043912}} {{MR|0036318}} {{ZBL|0508.01017}} {{ZBL|0445.30001}} {{ZBL|0213.35602}} {{ZBL|0146.30602}} {{ZBL|0196.33801}} {{ZBL|0100.28903}} {{ZBL|0178.08201}} {{ZBL|0114.28101}} {{ZBL|0071.07502}} {{ZBL|0066.32801}} {{ZBL|0052.30503}} {{ZBL|0050.08403}} {{ZBL|0048.05905}} {{ZBL|0048.05904}} {{ZBL|0042.31603}} {{ZBL|0041.41102}} {{ZBL|0029.25802}} {{ZBL|0018.26202}} {{ZBL|0015.36001}} {{ZBL|0006.26204}} </TD></TR><TR><TD valign="top">[20]</TD> <TD valign="top"> A. Pfluger, "Theorie der Riemannschen Flächen" , Springer (1957) {{MR|0084031}} {{ZBL|0077.07803}} </TD></TR><TR><TD valign="top">[21]</TD> <TD valign="top"> L. Sario, M. Nakai, "Classification theory of Riemann surfaces" , Springer (1970) {{MR|0264064}} {{ZBL|0199.40603}} </TD></TR><TR><TD valign="top">[22]</TD> <TD valign="top"> M. Heins, "Hardy classes on Riemann surfaces" , Springer (1969) {{MR|0247069}} {{ZBL|0176.03001}} </TD></TR><TR><TD valign="top">[23]</TD> <TD valign="top"> R.C. Gunning, "Lectures on Riemann surfaces" , Princeton Univ. Press (1966) {{MR|0207977}} {{ZBL|0175.36801}} </TD></TR><TR><TD valign="top">[24]</TD> <TD valign="top"> R.C. Gunning, "Lectures on Riemann surfaces: Jacobi varieties" , Princeton Univ. Press (1972) {{MR|0357407}} {{ZBL|0387.32008}} </TD></TR><TR><TD valign="top">[25]</TD> <TD valign="top"> O. Forster, "Lectures on Riemann surfaces" , Springer (1981) (Translated from German) {{MR|0648106}} {{ZBL|0475.30002}} </TD></TR></table> | <table><TR><TD valign="top">[1]</TD> <TD valign="top"> B. Riemann, "Collected works" , Dover, reprint (1953) {{MR|}} {{ZBL|0703.01020}} {{ZBL|08.0231.03}} </TD></TR><TR><TD valign="top">[2]</TD> <TD valign="top"> A.I. Markushevich, "Theory of functions of a complex variable" , '''1–2''' , Chelsea (1977) (Translated from Russian) {{MR|0444912}} {{ZBL|0357.30002}} </TD></TR><TR><TD valign="top">[3]</TD> <TD valign="top"> A. Hurwitz, R. Courant, "Vorlesungen über allgemeine Funktionentheorie und elliptische Funktionen" , Springer (1964) {{MR|0173749}} {{ZBL|0135.12101}} </TD></TR><TR><TD valign="top">[4]</TD> <TD valign="top"> S. Stoilov, "The theory of functions of a complex variable" , '''1–2''' , Moscow (1962) (In Russian; translated from Rumanian)</TD></TR><TR><TD valign="top">[5]</TD> <TD valign="top"> S. [S. Stoilov] Stoilow, "Leçons sur les principes topologiques de la théorie des fonctions analytiques" , Gauthier-Villars (1938) {{MR|0082545}} {{ZBL|0121.06103}} {{ZBL|0072.07604}} {{ZBL|0017.37802}} </TD></TR><TR><TD valign="top">[6]</TD> <TD valign="top"> G. Springer, "Introduction to Riemann surfaces" , Chelsea, reprint (1981) {{MR|0122987}} {{MR|1530201}} {{MR|0092855}} {{ZBL|0501.30039}} </TD></TR><TR><TD valign="top">[7]</TD> <TD valign="top"> R. Nevanlinna, "Uniformisierung" , Springer (1967) {{MR|0228671}} {{ZBL|0152.27401}} </TD></TR><TR><TD valign="top">[8]</TD> <TD valign="top"> M. Schiffer, D.C. Spencer, "Functionals of finite Riemann surfaces" , Princeton Univ. Press (1954) {{MR|0065652}} {{ZBL|0059.06901}} </TD></TR><TR><TD valign="top">[9]</TD> <TD valign="top"> N.G. Chebotarev, "The theory of algebraic functions" , Moscow-Leningrad (1948) (In Russian)</TD></TR><TR><TD valign="top">[10]</TD> <TD valign="top"> L.I. Volkovyskii, "Investigation of the type problem for a simply-connected Riemann surface" ''Trudy Mat. Inst. Steklov.'' , '''34''' (1950) pp. 3–171 (In Russian) {{MR|0049330}} {{ZBL|}} </TD></TR><TR><TD valign="top">[11]</TD> <TD valign="top"> L.I. Volkovyskii, "Contempory studies on Riemann surfaces" ''Uspekhi Mat. Nauk'' , '''11''' : 5 (1956) pp. 77–84 (In Russian)</TD></TR><TR><TD valign="top">[12]</TD> <TD valign="top"> S.L. Krushkal', "Quasi-conformal mappings and Riemann surfaces" , Winston & Wiley (1979) (Translated from Russian) {{MR|536488}} {{ZBL|}} </TD></TR><TR><TD valign="top">[13]</TD> <TD valign="top"> S.L. Krushkal', B.N. Apanasov, N.A. Gusevskii, "Kleinian groups and uniformization in examples and problems" , Amer. Math. Soc. (1986) (Translated from Russian) {{MR|0835439}} {{ZBL|0579.30001}} </TD></TR><TR><TD valign="top">[14]</TD> <TD valign="top"> E.B. Vinberg, O.V. Shvartsman, "Riemann surfaces" ''J. Soviet Math.'' , '''14''' : 1 (1980) pp. 985–1020 ''Itogi Nauk. i Tekhn. Algebra. Topol. Geom.'' , '''16''' (1978) pp. 191–245 {{MR|0538254}} {{ZBL|0445.30032}} </TD></TR><TR><TD valign="top">[15a]</TD> <TD valign="top"> L. Bers, "Quasi-conformal mappings and Teichmüller's theorem" R. Nevanlinna (ed.) et al. (ed.) , ''Analytic functions'' , Princeton Univ. Press (1960) pp. 89–119 {{MR|114898}} {{ZBL|}} </TD></TR><TR><TD valign="top">[15b]</TD> <TD valign="top"> L.V. Ahlfors, "The complex analytic structure of the space of closed Riemann surfaces" R. Nevanlinna (ed.) et al. (ed.) , ''Analytic functions'' , Princeton Univ. Press (1960) pp. 45–66 {{MR|0124486}} {{ZBL|0100.28903}} </TD></TR><TR><TD valign="top">[15c]</TD> <TD valign="top"> L. Bers, "Spaces of Riemann surfaces" J.A. Todd (ed.) , ''Proc. Internat. Congress Mathematicians (Edinburgh, 1958)'' , Cambridge Univ. Press (1960) pp. 349–361 {{MR|0124484}} {{MR|0111835}} {{ZBL|0116.28803}} {{ZBL|0106.28501}} </TD></TR><TR><TD valign="top">[15d]</TD> <TD valign="top"> L. Bers, "Simultaneous uniformization" ''Bull. Amer. Math. Soc.'' , '''66''' (1960) pp. 94–97 {{MR|0111834}} {{ZBL|0090.05101}} </TD></TR><TR><TD valign="top">[15e]</TD> <TD valign="top"> L. Bers, "Holomorphic differentials as functions of moduli" ''Bull. Amer. Math. Soc.'' , '''67''' (1961) pp. 206–210 {{MR|0122989}} {{ZBL|0102.06702}} </TD></TR><TR><TD valign="top">[15f]</TD> <TD valign="top"> L. Ahlfors, "On quasiconformal mappings" ''J. d'Anal. Math.'' , '''3''' (1954) pp. 1–58; 207–208 {{MR|0064875}} {{ZBL|0057.06506}} </TD></TR><TR><TD valign="top">[16a]</TD> <TD valign="top"> L. Bers, "Uniformization, moduli, and Kleinian groups" ''Bull. London Math. Soc.'' , '''4''' (1972) pp. 257–300 {{MR|0348097}} {{ZBL|0257.32012}} </TD></TR><TR><TD valign="top">[16b]</TD> <TD valign="top"> L. Bers, "The moduli of Kleinian groups" ''Russian Math. Surveys'' , '''29''' : 2 (1974) pp. 88–102 ''Uspekhi Mat. Nauk'' , '''29''' : 2 (1974) pp. 86–102 {{MR|0422691}} {{ZBL|}} </TD></TR><TR><TD valign="top">[17]</TD> <TD valign="top"> F. Klein, "Riemannschen Flächen" , Springer, reprint (1986)</TD></TR><TR><TD valign="top">[18]</TD> <TD valign="top"> H. Weyl, "The concept of a Riemann surface" , Addison-Wesley (1955) (Translated from German) {{MR|1440406}} {{MR|0166351}} {{ZBL|}} </TD></TR><TR><TD valign="top">[19]</TD> <TD valign="top"> L.V. Ahlfors, L. Sario, "Riemann surfaces" , Princeton Univ. Press (1974) {{MR|0667739}} {{MR|0712145}} {{MR|0279300}} {{MR|0204641}} {{MR|0130368}} {{MR|0124486}} {{MR|0114911}} {{MR|0093583}} {{MR|0083561}} {{MR|1565732}} {{MR|0090649}} {{MR|0055250}} {{MR|0054729}} {{MR|0054055}} {{MR|0043912}} {{MR|0036318}} {{ZBL|0508.01017}} {{ZBL|0445.30001}} {{ZBL|0213.35602}} {{ZBL|0146.30602}} {{ZBL|0196.33801}} {{ZBL|0100.28903}} {{ZBL|0178.08201}} {{ZBL|0114.28101}} {{ZBL|0071.07502}} {{ZBL|0066.32801}} {{ZBL|0052.30503}} {{ZBL|0050.08403}} {{ZBL|0048.05905}} {{ZBL|0048.05904}} {{ZBL|0042.31603}} {{ZBL|0041.41102}} {{ZBL|0029.25802}} {{ZBL|0018.26202}} {{ZBL|0015.36001}} {{ZBL|0006.26204}} </TD></TR><TR><TD valign="top">[20]</TD> <TD valign="top"> A. Pfluger, "Theorie der Riemannschen Flächen" , Springer (1957) {{MR|0084031}} {{ZBL|0077.07803}} </TD></TR><TR><TD valign="top">[21]</TD> <TD valign="top"> L. Sario, M. Nakai, "Classification theory of Riemann surfaces" , Springer (1970) {{MR|0264064}} {{ZBL|0199.40603}} </TD></TR><TR><TD valign="top">[22]</TD> <TD valign="top"> M. Heins, "Hardy classes on Riemann surfaces" , Springer (1969) {{MR|0247069}} {{ZBL|0176.03001}} </TD></TR><TR><TD valign="top">[23]</TD> <TD valign="top"> R.C. Gunning, "Lectures on Riemann surfaces" , Princeton Univ. Press (1966) {{MR|0207977}} {{ZBL|0175.36801}} </TD></TR><TR><TD valign="top">[24]</TD> <TD valign="top"> R.C. Gunning, "Lectures on Riemann surfaces: Jacobi varieties" , Princeton Univ. Press (1972) {{MR|0357407}} {{ZBL|0387.32008}} </TD></TR><TR><TD valign="top">[25]</TD> <TD valign="top"> O. Forster, "Lectures on Riemann surfaces" , Springer (1981) (Translated from German) {{MR|0648106}} {{ZBL|0475.30002}} </TD></TR></table> | ||
| − | |||
| − | |||
====Comments==== | ====Comments==== | ||
| − | For the generalization to "Riemann surfaces over | + | For the generalization to "Riemann surfaces over $\mathbf C^n$" see, e.g., [[#References|[a6]]] and [[Riemannian domain|Riemannian domain]]. |
====References==== | ====References==== | ||
<table><TR><TD valign="top">[a1]</TD> <TD valign="top"> P.A. Griffiths, J.E. Harris, "Principles of algebraic geometry" , Wiley (Interscience) (1978) {{MR|0507725}} {{ZBL|0408.14001}} </TD></TR><TR><TD valign="top">[a2]</TD> <TD valign="top"> P. Griffiths, "Introduction to algebraic curves" , Amer. Math. Soc. (1989) {{MR|1013999}} {{ZBL|0696.14012}} </TD></TR><TR><TD valign="top">[a3]</TD> <TD valign="top"> H.M. Farkas, I. Kra, "Riemann surfaces" , Springer (1980) pp. Sect. III.6 {{MR|0583745}} {{ZBL|0475.30001}} </TD></TR><TR><TD valign="top">[a4]</TD> <TD valign="top"> H. Behnke, F. Sommer, "Theorie der analytischen Funktionen einer komplexen Veränderlichen" , Springer (1955) {{MR|0073682}} {{ZBL|0065.06102}} </TD></TR><TR><TD valign="top">[a5]</TD> <TD valign="top"> H. Cohn, "Conformal mapping on Riemann surfaces" , Dover, reprint (1980) {{MR|0594937}} {{ZBL|0493.30001}} </TD></TR><TR><TD valign="top">[a6]</TD> <TD valign="top"> H. Behnke, P. Thullen, "Theorie der Funktionen meherer komplexer Veränderlichen" , Springer (1970) pp. Chapt. VI (Elraged & Revised Edition. Original: 1934)</TD></TR><TR><TD valign="top">[a7]</TD> <TD valign="top"> W. Osgood, "Lehrbuch der Funktionentheorie" , '''1–2''' , Chelsea, reprint (1965) {{MR|0196039}} {{MR|0196038}} {{ZBL|0005.29904}} {{ZBL|58.0390.04}} {{ZBL|54.0326.10}} {{ZBL|55.0171.02}} {{ZBL|50.0209.04}} {{ZBL|43.0476.02}} {{ZBL|37.0409.02}} {{ZBL|38.0412.01}} </TD></TR></table> | <table><TR><TD valign="top">[a1]</TD> <TD valign="top"> P.A. Griffiths, J.E. Harris, "Principles of algebraic geometry" , Wiley (Interscience) (1978) {{MR|0507725}} {{ZBL|0408.14001}} </TD></TR><TR><TD valign="top">[a2]</TD> <TD valign="top"> P. Griffiths, "Introduction to algebraic curves" , Amer. Math. Soc. (1989) {{MR|1013999}} {{ZBL|0696.14012}} </TD></TR><TR><TD valign="top">[a3]</TD> <TD valign="top"> H.M. Farkas, I. Kra, "Riemann surfaces" , Springer (1980) pp. Sect. III.6 {{MR|0583745}} {{ZBL|0475.30001}} </TD></TR><TR><TD valign="top">[a4]</TD> <TD valign="top"> H. Behnke, F. Sommer, "Theorie der analytischen Funktionen einer komplexen Veränderlichen" , Springer (1955) {{MR|0073682}} {{ZBL|0065.06102}} </TD></TR><TR><TD valign="top">[a5]</TD> <TD valign="top"> H. Cohn, "Conformal mapping on Riemann surfaces" , Dover, reprint (1980) {{MR|0594937}} {{ZBL|0493.30001}} </TD></TR><TR><TD valign="top">[a6]</TD> <TD valign="top"> H. Behnke, P. Thullen, "Theorie der Funktionen meherer komplexer Veränderlichen" , Springer (1970) pp. Chapt. VI (Elraged & Revised Edition. Original: 1934)</TD></TR><TR><TD valign="top">[a7]</TD> <TD valign="top"> W. Osgood, "Lehrbuch der Funktionentheorie" , '''1–2''' , Chelsea, reprint (1965) {{MR|0196039}} {{MR|0196038}} {{ZBL|0005.29904}} {{ZBL|58.0390.04}} {{ZBL|54.0326.10}} {{ZBL|55.0171.02}} {{ZBL|50.0209.04}} {{ZBL|43.0476.02}} {{ZBL|37.0409.02}} {{ZBL|38.0412.01}} </TD></TR></table> | ||
Latest revision as of 13:13, 6 January 2022
of an analytic function $ w = f( z) $ of a complex variable $ z $
A surface $ R $ such that the complete analytic function $ w = f( z) $, which is, in general, multiple-valued, can be considered as a single-valued analytic function $ w = F( p) $ of a point $ p $ on $ R $.
The concept of a Riemann surface arose in connection with the studies of algebraic functions $ w = f( z) $ defined by an algebraic equation
$$ \tag{1 } a _ {0} ( z) w ^ {m} + a _ {1} ( z) w ^ {m- 1} + \dots + a _ {m} ( z) = 0, $$
where $ a _ {j} ( z) $, $ j = 0 \dots m $, are polynomials with constant coefficients, $ a _ {0} ( z) \neq 0 $, $ a _ {m} ( z) \neq 0 $. In the works of V. Puiseux (1850–1851) one discovers a clear understanding of multiple-valuedness, characteristic of these functions $ w = f( z) $, when to each value of the variable $ z $, $ m $ values of the variable $ w $ correspond. B. Riemann (1851–1857, see [1]) was the first to show how for any algebraic function one can construct a surface on which this function can be considered as a single-valued rational function of the point. The obtained Riemann surface can be identified with the algebraic curve defined by equation (1). In general, a mutual penetration (sometimes more intensive, sometimes less intensive) of ideas and methods of the theory of functions of a complex variable on the one hand and of algebra and algebraic geometry on the other hand is characteristic of the whole period of further development of the theory of Riemann surfaces, associated with the names of F. Klein, H. Poincaré, P. Koebe, and others. The landmark of this development was the first edition of the book of H. Weyl [18], in which the general concept of an abstract Riemann surface was formulated.
Definition A: A connected topological Hausdorff space $ R $ is called an abstract Riemann surface or, simply, a Riemann surface, if it admits a covering by open sets $ U $ together with a homeomorphism $ \alpha : U \rightarrow D $ corresponding to each set $ U $, where $ D = \{ {z \in \mathbf C } : {| z | < 1 } \} $ is the unit disc in the complex $ z $-plane $ \mathbf C $; moreover, if a point $ p \in R $ belongs to $ U $ and $ U ^ \prime $, then the one-to-one correspondence $ z ^ \prime = \alpha ^ \prime \alpha ^ {- 1} ( z) $ should be a conformal mapping of the first kind in a neighbourhood of the point $ \alpha ( p) \in D $, that is, $ z ^ \prime = \alpha ^ \prime \alpha ^ {- 1} ( z) $ is a univalent analytic function in a neighbourhood of the point $ \alpha ( p) \in D $. In other words, an abstract Riemann surface is a two-dimensional complex-analytic manifold.
The definition of a Riemann surface with boundary $ \overline{R} $ differs from definition $ A $ by the fact that together with the homeomorphisms $ \alpha : U \rightarrow D $, homeomorphisms $ \alpha : U \rightarrow D _ {0} ^ {+} $ are admitted, where $ D _ {0} ^ {+} = \{ {z \in \mathbf C } : {| z | < 1, \mathop{\rm Im} z \geq 0 } \} $ is the unit upper half-disc in $ \mathbf C $; moreover, it is usually assumed that $ \overline{R} $ is not already a Riemann surface in the sense of definition $ A $. The points of a Riemann surface with boundary $ \overline{R} $ that have neighbourhoods homeomorphic to $ D $ are called interior and the other points, that are mapped to the points of the segment
$$ \{ {z = x + iy \in \mathbf C } : {- 1 < x < 1, y = 0 } \} , $$
form the boundary $ \partial \overline{R} $. The set of interior points of $ \overline{R} $ (the interior of $ \overline{R} $) is a Riemann surface in the sense of definition $ A $. Thus, in the case of a Riemann surface with boundary, the boundary is usually considered to be a non-empty set.
A Riemann surface (with boundary) is a triangulable and orientable manifold with a countable base and, hence, it is separable and metrizable. A compact Riemann surface (without boundary) is called a closed Riemann surface; the wider class of finite Riemann surfaces includes the closed Riemann surfaces and the compact Riemann surfaces with a boundary consisting of a finite number of connected components. Non-compact Riemann surfaces with boundary or without it are called open Riemann surfaces. In certain cases it is more convenient to admit in definition $ A $ not only conformal mappings of the first kind but also conformal mappings of the second kind. A Riemann surface with boundary $ \overline{R}\; $( or without it) obtained using such an approach is, generally speaking, not orientable any more, but under the assumption that it be finite it can be conformally imbedded in an orientable closed Riemann surface: the double of $ \overline{R} $ (see [8], cf. Double of a Riemann surface).
Let an analytic function $ w = f( z) $ be given by one of its regular elements $ ( a, P) = ( a, P( z- a)) $, i.e. by a pair consisting of a point $ a \in \mathbf C $ and a power series
$$ P( z- a) = \sum _ {\nu = 0 } ^ \infty a _ \nu ( z- a) ^ \nu $$
with centre $ a $ and radius of convergence $ r( a) $, $ 0 < r( a) \leq \infty $. Analytic continuation of the element $ ( a, P) $ along all possible paths in the extended plane $ \overline{\mathbf C} $ allows one to obtain all regular elements $ ( b, Q) $ of the same type; in their totality they form the complete analytic function, which is also denoted by $ w = f( z) $. Moreover, under analytic continuation elements of a more general nature arise:
$$ ( b, S) = ( b, S(( z- b) ^ {1/n} )), $$
i.e. pairs consisting of a point $ b \in \overline{\mathbf C} $ and a generalized power series (a Puiseux series):
$$ S(( z- b) ^ {1/n} ) = \sum _ {\nu = m } ^ \infty b _ {n} ( z- b) ^ {\nu /n } $$
or (in the case when $ b = \infty $ is the point at infinity):
$$ S( z ^ {- 1/n} ) = \sum _ {\nu = m } ^ \infty b _ \nu z ^ {- \nu /n } , $$
where $ m $ is an integer and $ n $ is a positive integer. Moreover, these series converge when $ | z- b | < r( b) $ or $ | z | > r( \infty ) > 0 $, respectively. The generalized elements $ ( b, S) $ or, more precisely, their equivalence classes, form in their totality the analytic image $ A _ {f} $ corresponding to the given analytic function $ w = f( z) $. Among the equivalence classes of elements $ ( b, S) $ that form the analytic image one can distinguish regular ones, when $ n= 1 $, and ramified ones, when $ n> 1 $. The introduction of an appropriate topology on the analytic image $ A _ {f} $ will turn it into the Riemann surface $ R _ {f} $ of the analytic function $ w = f( z) $. This can be achieved, for example, by defining the neighbourhood of an element $ ( b, S) $, $ b \neq \infty $, as the set consisting of the element $ ( b, S) $ itself and all the regular elements $ ( a, P) $ of $ A _ {f} $ for which $ | b- a | < \rho ^ {n} $, $ \rho < r( b) $, and the series $ P( z- a) $ converges to one of the $ n $ determinations of the series $ S(( z- b) ^ {1/n} ) $ in their common domain of definition, i.e.
$$ P( z- a) \equiv S( \epsilon ( z- b) ^ {1/n} ), $$
where $ \epsilon $ is one of the $ n $-th order roots of unity, $ \epsilon ^ {n} = 1 $. The neighbourhood of the element $ ( \infty , S) $ consists of the element $ ( \infty , S) $ itself and all those regular elements $ ( a, P) $ of $ A _ {f} $ for which $ | a | > \rho ^ {- 1} $, $ \rho < r( b) $, and the series $ P( z- a) $ converges to one of the $ n $ determinations of the series $ S( z ^ {- 1/n} ) $. The space $ R _ {f} $ satisfies all the conditions of definition $ A $.
Thus, to any analytic function $ w = f( z) $ corresponds a Riemann surface $ R _ {f} $ on which this function is a single-valued analytic function $ w = F( p) $ of a point $ p = ( b, S) \in R _ {f} $. This means that in a neighbourhood of any point $ p _ {0} = ( b, S) $ there exists a local uniformizing parameter $ t = ( z- b) ^ {1/n} $ in which $ w $ is represented as a single-valued analytic function $ w = P( t) = F( p) $. In other words, the Riemann surface $ R _ {f} $ of an analytic function is a geometric construct that is used for the global uniformization of a, generally speaking, multiple-valued relation $ w = f( z) $. In a neighbourhood of each point $ p _ {0} = ( b, S) \in R _ {f} $ this relation is uniformized by the two single-valued analytic functions $ z = b+ t ^ {n} $ and $ w = S( t) $. On the other hand, the projection $ \pi : ( b, S) \rightarrow b $ that takes each element $ p _ {0} = ( b, S) \in R _ {f} $ to its centre $ b $ shows that the Riemann surface $ R _ {f} $ of an analytic function is a (ramified) covering surface over the extended complex plane $ \overline{\mathbf C}\; $ or, which is the same, over the Riemann sphere. The projections of the ramified elements $ ( b, S) $ with $ n > 1 $ are branch points of this covering.
At the same time, to each a priori given Riemann surface $ R $ correspond infinitely-many analytic functions $ w = f( z) $ with precisely $ R $ as Riemann surface, $ R _ {f} = R $. For the case of closed Riemann surfaces this statement was formulated and proved already by Riemann in 1851. The central point of the corresponding proof is the construction on $ R $ of harmonic functions with given singularities. The proof given by Riemann was based on an uncritical application of the so-called Dirichlet principle; Koebe (1909) was the first to give a rigorous proof; later there appeared simpler proofs of this fundamental statement, among them those based on the properly applied Dirichlet principle (see, e.g. [3], [4], [17], [18]).
Whatever the orientable topological surface $ S $ may be, one can construct a Riemann surface $ R $ homeomorphic to $ S $, i.e. a Riemann surface of the same topological type as $ S $. Closed Riemann surfaces are topologically completely determined by one number — the genus $ g $, $ 0 \leq g < + \infty $( cf. Genus of a surface). The topological type of such a Riemann surface $ R $ for $ g = 0 $ is a sphere, for $ g = 1 $— a torus, for $ g > 1 $— a generalized torus, or a sphere with $ g $ handles. By cutting a Riemann surface $ R $ of genus $ g = 0 $ along some arc one obtains a digon with the symbol $ s = aa ^ {- 1} $ as its topological model or normal form, indicating that the points of the sides $ a $ and $ a ^ {- 1} $ are identified; when $ g \geq 1 $ one has to carry out $ 2g $ canonical sections $ a _ {1} , b _ {1} \dots a _ {g} , b _ {g} $, after which one obtains the normal form of a closed Riemann surface $ R $— a polygon with $ 4g $ pairwise-identified sides; the symbol $ s = a _ {1} \dots $ should indicate the order of appearance of the sides. For instance, in Fig. athe normal forms of a sphere for $ g= 0 $ and a torus for $ g= 1 $ are shown together with their symbols.
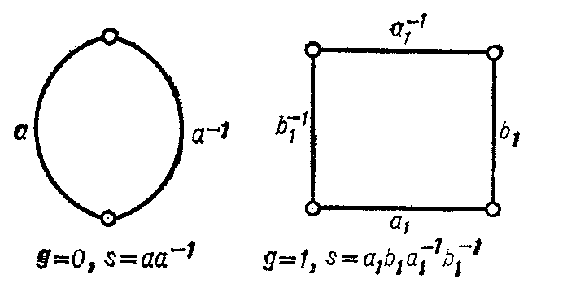
Figure: r082040a
From the analytic point of view a closed Riemann surface $ R $ is characterized by the fact that it is the Riemann surface of some algebraic function $ w = f( z) $ defined by an algebraic equation (1) of degree $ m $. This Riemann surface $ R $ can be imagined as $ m $ sheets extending over the Riemann sphere and mutually connected in a certain manner at the branch points and along some lines connecting these points (the manner of connecting is determined by the specific form of equation (1)). The genus $ g $ of the Riemann surface $ R $ can in this case be expressed as a function of the number of sheets $ m $ and the orders $ k _ {1} \dots k _ {s} $ of the branch points by the Riemann–Hurwitz formula
$$ g = \sum _ {\nu = 1 } ^ { s } \frac{k _ \nu - 1 }{2} - m + 1. $$
Finite Riemann surfaces $ \overline{R}\; $ are topologically completely characterized by the genus $ g $, $ 0 \leq g < \infty $, and the number $ l $ of connected components of the boundary; their topological type is a sphere with $ g $ handles and $ l $ holes. In the normal form of a finite Riemann surface, the number of sides is not necessarily even, some sides corresponding to components of the boundary that remain free are not identified. The notion of the genus can also be generalized to open Riemann surfaces $ R $, for example by exhausting $ R $ by a sequence $ \{ \overline{R} _ \nu \} _ {\nu = 1 } ^ \infty $ of compact Riemann surfaces with boundary $ \overline{R} _ \nu $, belonging to $ R $, and such that $ \overline{R} _ \nu $ is contained in $ \overline{R} _ {\nu + 1 } $, $ \cup _ {\nu = 1 } ^ \infty \overline{R} _ \nu = R $. The genus $ g $ of $ R $ is set equal to $ g = \lim\limits _ {\nu \rightarrow \infty } g _ \nu $, where $ g _ \nu $ is the genus of $ \overline{R} _ \nu $. This limit exists and is independent of the choice of the exhaustion $ \{ \overline{R} _ \nu \} $, $ 0 \leq g \leq + \infty $. However, the genus does not completely define the topological type of an open Riemann surface; the topological types of open Riemann surfaces can be rather diverse. Thus, in Fig.2a, Fig.2b two models with $ g= 0 $ and $ g= 2 $, respectively, are shown.
An important topological characteristic of a Riemann surface $ R $ is the order of connectivity: $ R $ is called simply connected if any simple closed curve in $ R $ can be deformed continuously into a point without getting out of $ R $, i.e. in other words, if the fundamental group of $ R $ is trivial. Otherwise the Riemann surface $ R $ is called multiply connected. The schlichtartig Riemann surfaces form an important class of Riemann surfaces; they are the Riemann surfaces (with boundary or without) that are split by any simple closed curve into non-intersecting parts. For example, in Fig.2a a topological model of a multiply-connected schlichtartig Riemann surface is shown. A schlichtartig Riemann surface necessarily has genus zero. A schlichtartig Riemann surface $ R $ is called $ n $-connected if the minimum number of sections necessary to convert $ R $ to a simply-connected Riemann surface is equal to $ n- 1 $, $ n \geq 1 $ (see Fig.2b).
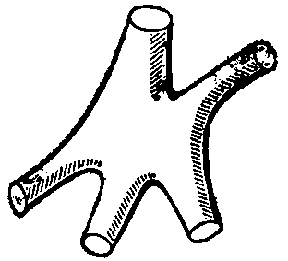
Figure: r082040b
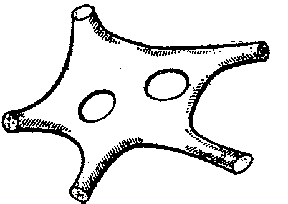
Figure: r082040c
The topological properties of a Riemann surface $ R $ do not completely characterize the analytic properties of $ R $, i.e. the topological properties of $ R $ do not completely characterize the behaviour of functions of different classes on $ R $. In particular, let $ f: R _ {1} \rightarrow R _ {2} $ be a function on the Riemann surface $ R _ {1} $ with values on another Riemann surface $ R _ {2} $. The function $ f $ is called analytic on $ R _ {1} $ if for any point $ p _ {0} \in R _ {1} $, $ f( p _ {0} ) = q _ {0} $, one can find local uniformizing parameters $ t = \phi ( p) $ in a neighbourhood of $ p _ {0} $ on $ R _ {1} $ and $ \tau = \psi ( q) $ in a neighbourhood of $ q _ {0} $ on $ R _ {2} $, respectively, such that the composite function
$$ \tau = \psi \{ f[ \phi ^ {- 1} ( t)] \} = g( t) $$
is an analytic function of the complex variable $ t $ in a neighbourhood of the value $ t _ {0} = \phi ( p _ {0} ) $. Two Riemann surfaces $ R _ {1} $ and $ R _ {2} $ are called conformally equivalent, or are said to belong to the same conformal class (cf. Riemann surfaces, conformal classes of), if there exists an analytic function $ f: R _ {1} \rightarrow R _ {2} $ that gives a one-to-one mapping from $ R _ {1} $ onto $ R _ {2} $. From the point of view of the behaviour of analytic functions on Riemann surfaces, conformally-equivalent Riemann surfaces are considered as one and the same Riemann surface, but topologically-equivalent Riemann surfaces are not always conformally equivalent.
In terms of Riemann surfaces, the Riemann mapping theorem can be formulated as follows: Any simply-connected Riemann surface is conformally equivalent to one of the following three domains: 1) the extended complex plane $ \overline{\mathbf C} = \mathbf C \cup \{ \infty \} $, i.e. the Riemann sphere (the elliptic case); 2) the finite complex plane $ \mathbf C $, i.e. the punctured Riemann sphere (the parabolic case); or 3) the unit disc $ D = \{ {z \in \mathbf C } : {| z | < 1 } \} $ in $ \mathbf C $, i.e. the Riemann sphere with a section of positive length (the hyperbolic case). An important result is that any schlichtartig Riemann surface is conformally equivalent to some canonical domain in the extended complex plane. As such a canonical domain one may take the entire extended plane with a finite or infinite number of sections parallel to the real axis; moreover, some of these sections may degenerate into points. As mentioned above, in the case of a simply-connected Riemann surface the canonical domain either has no sections (elliptic type), or the section degenerates into a point (parabolic type), or the section has a positive length (hyperbolic type). All three types of simply-connected Riemann surfaces are conformally different, although the last two of them are topologically equivalent. The problem of types, which has not yet (1991) been solved completely, consists in finding additional conditions under which a simply-connected Riemann surface will be of hyperbolic or parabolic type (see [6], [7], [10], [11], and Riemann surfaces, classification of).
In the case of an arbitrary Riemann surface $ R $, its universal covering surface $ \widehat{R} $ will always be a simply-connected Riemann surface, and thus belongs to one of the three types above. The Riemann surface $ R $ itself is considered to be of elliptic, parabolic or hyperbolic type, according to the type of its universal covering $ \widehat{R} $. This classification of Riemann surfaces is justified by the following considerations. Let $ D $ be one of three domains: the extended complex plane, the finite complex plane or the open unit disc, and let $ \Lambda $ be some group of Möbius transformations of $ D $ onto itself (automorphisms) without fixed points in $ D $. A conformal mapping $ w = W( q) $ of the universal covering $ \widehat{R} $ onto $ D $ carries the group $ \widehat \Lambda $ of transformations of the covering $ \widehat{R} $, which is isomorphic to the fundamental group $ \pi _ {1} ( R) $, onto some group $ \Lambda $ of automorphisms of $ D $. Moreover, $ w = W( q) $ can be considered as a conformal mapping from the quotient space $ \widehat{R} / \widehat \Lambda $ onto the quotient space $ D/ \Lambda $, and $ \widehat{R} / \widehat \Lambda $ can be identified with $ R $. Thus, $ w = W( q) $ can be considered as a conformal mapping from the Riemann surface $ R $ onto the quotient space $ D/ \Lambda $ with some group of automorphisms $ \Lambda $ isomorphic to the fundamental group $ \pi _ {1} ( R) $.
Since a Riemann surface $ R $ of elliptic type is necessarily simply-connected, the group $ \Lambda $ is trivial and thus such a Riemann surface is necessarily the Riemann surface of the function inverse to a rational function. A simply-connected Riemann surface of parabolic type is necessarily the Riemann surface of the function inverse to a meromorphic function in the finite plane. A compact Riemann surface of genus $ g= 0 $, $ g= 1 $ or $ g > 1 $ is a Riemann surface of elliptic, parabolic or hyperbolic type, respectively.
In connection with the conformal equivalence of Riemann surfaces there arises the question of the structure of the group $ \Sigma $ of conformal automorphisms of a Riemann surface $ R $. Except for certain simple cases, this group $ \Sigma $ is discrete and for compact Riemann surfaces of genus $ g > 1 $ it is finite (Schwarz' theorem). There are only seven exceptional cases in which the group $ \Sigma $ is continuous, namely (representatives of the corresponding conformal classes are given): the sphere in the elliptic case; the sphere with one or two punctures and the torus in the parabolic case; the open disc, the punctured open disc and an annulus in the hyperbolic case.
Of great importance also is the moduli problem for Riemann surfaces in its different versions (cf. Moduli of a Riemann surface; Moduli problem). It is the problem of the possible description of the diversity of conformally-inequivalent Riemann surfaces of different types. For example, it is easy to establish the following facts. The set of types of conformally-inequivalent doubly-connected schlichtartig Riemann surfaces (annuli) depends on one real parameter (the modulus) $ k $, $ 0 < k < 1 $; i.e. two annuli $ 0 < r _ \nu < | z | < R _ \nu $, $ \nu = 1, 2 $, are conformally equivalent if and only if the ratios of their radii $ k = ( r _ {1} /R _ {1} ) = ( r _ {2} / R _ {2} ) $ coincide. The set of types of conformally-inequivalent $ n $-connected schlichtartig Riemann surfaces for $ n > 2 $ depends on $ 3n- 6 $ real parameters. The set of types of conformally-inequivalent closed Riemann surfaces of genus $ g \geq 1 $ for $ g= 1 $ depends on two real parameters and for $ g > 1 $ on $ 6g- 6 $ real parameters (see Riemann surfaces, conformal classes of, and also [3], [12], [13], , ; concerning the behaviour of functions of other classes on Riemann surfaces see Riemann surfaces, classification of).
An important aspect of the theory of Riemann surfaces is its connection with the concept of uniformization. In general, for a multiple-valued analytic function
$$ \tag{2 } w = f( z), $$
its Riemann surface $ R _ {f} $ provides a geometrical means of uniformization: The multiple-valued relation (2) is replaced by two single-valued relations
$$ \tag{3 } w = F( p),\ \ z = g( p),\ \ p \in R _ {f} , $$
which give a single-valued expression of $ z $ and $ w $ in the entire domain of definition of the function (2) as a complete analytic function. On the other hand, the approach of K. Weierstrass to the construction of the notion of the complete analytic function of (2) is based on the use of a local uniformizing parameter $ t $ that allows one to express the variables $ z $ and $ w $ analytically as single-valued analytic functions $ z = z( t) $ and $ w = w( t) $, locally in a neighbourhood of some point $ ( z _ {0} , w _ {0} ) $, $ w _ {0} = f( z _ {0} ) $. The uniformization problem in its simplest classical form is the problem of synthesis of these two ideas. One has to replace the relation (2) in its entire domain of definition by two analytic representations $ z = z( t) $, $ w = w( t) $, where $ t $ is a uniformizing complex variable with values in some domain of the plane.
The above-mentioned statement of the possibility of uniformization was established by Koebe and, independently, by Poincaré almost simultaneously in 1907. If the Riemann surface $ R _ {f} $ of the function (2) is simply connected or schlichtartig, then the uniformization problem is reduced to constructing a conformal mapping $ \phi : R _ {f} \rightarrow D $ from $ R _ {f} $ onto the planar domain $ D $. The representations (3) then provide the sought uniformization:
$$ z = g[ \phi ^ {- 1} ( t)],\ \ w = F[ \phi ^ {- 1} ( t)],\ \ t \in D. $$
A conformal mapping $ f $ onto a planar domain exists only for the schlichtartig Riemann surfaces $ R _ {f} $ (the general uniformization theorem).
In the general case of an arbitrary analytic relation (2), the Riemann surface $ R _ {f} $ is not schlichtartig but its universal covering surface $ \widehat{R} _ {f} $ is simply connected and, hence, there exists a conformal mapping
$$ \psi : \widehat{R} _ {f} \rightarrow D, $$
where $ D $ is one of the already-mentioned domains: $ \overline{\mathbf C} $, $ \mathbf C $ or the open unit disc. The function $ w = f( z) $ is meromorphic on the Riemann surface $ \widehat{R} _ {f} $ and, hence, it is also meromorphic on $ R _ {f} $; moreover, it depends only on the projection $ p = p( q) $, $ p \in R _ {f} $, of a point $ q \in \widehat{R} _ {f} $. Thus one obtains a geometrical uniformization in the form
$$ z = g[ p( q)],\ \ w = F[ p( q)], $$
and from it the analytic uniformization
$$ z = g \{ p[ \psi ^ {- 1} ( t) ] \} = \Psi ( t), $$
$$ w = F \{ p[ \psi ^ {- 1} ( t) ] \} = \Phi ( t),\ t \in D, $$
where $ z $ and $ w $ are expressed as meromorphic functions $ \Phi ( t) $ and $ \Psi ( t) $ of a variable $ t \in D $. These functions $ \Phi ( t) $ and $ \Psi ( t) $ are automorphic functions (cf. Automorphic function) in $ D $ relative to the group of automorphisms $ \Lambda $ isomorphic to the fundamental group $ \pi _ {1} ( R _ {f} ) $ of the Riemann surface $ R _ {f} $ of the uniformizing function (see [3], [7], , ).
References
| [1] | B. Riemann, "Collected works" , Dover, reprint (1953) Zbl 0703.01020 Zbl 08.0231.03 |
| [2] | A.I. Markushevich, "Theory of functions of a complex variable" , 1–2 , Chelsea (1977) (Translated from Russian) MR0444912 Zbl 0357.30002 |
| [3] | A. Hurwitz, R. Courant, "Vorlesungen über allgemeine Funktionentheorie und elliptische Funktionen" , Springer (1964) MR0173749 Zbl 0135.12101 |
| [4] | S. Stoilov, "The theory of functions of a complex variable" , 1–2 , Moscow (1962) (In Russian; translated from Rumanian) |
| [5] | S. [S. Stoilov] Stoilow, "Leçons sur les principes topologiques de la théorie des fonctions analytiques" , Gauthier-Villars (1938) MR0082545 Zbl 0121.06103 Zbl 0072.07604 Zbl 0017.37802 |
| [6] | G. Springer, "Introduction to Riemann surfaces" , Chelsea, reprint (1981) MR0122987 MR1530201 MR0092855 Zbl 0501.30039 |
| [7] | R. Nevanlinna, "Uniformisierung" , Springer (1967) MR0228671 Zbl 0152.27401 |
| [8] | M. Schiffer, D.C. Spencer, "Functionals of finite Riemann surfaces" , Princeton Univ. Press (1954) MR0065652 Zbl 0059.06901 |
| [9] | N.G. Chebotarev, "The theory of algebraic functions" , Moscow-Leningrad (1948) (In Russian) |
| [10] | L.I. Volkovyskii, "Investigation of the type problem for a simply-connected Riemann surface" Trudy Mat. Inst. Steklov. , 34 (1950) pp. 3–171 (In Russian) MR0049330 |
| [11] | L.I. Volkovyskii, "Contempory studies on Riemann surfaces" Uspekhi Mat. Nauk , 11 : 5 (1956) pp. 77–84 (In Russian) |
| [12] | S.L. Krushkal', "Quasi-conformal mappings and Riemann surfaces" , Winston & Wiley (1979) (Translated from Russian) MR536488 |
| [13] | S.L. Krushkal', B.N. Apanasov, N.A. Gusevskii, "Kleinian groups and uniformization in examples and problems" , Amer. Math. Soc. (1986) (Translated from Russian) MR0835439 Zbl 0579.30001 |
| [14] | E.B. Vinberg, O.V. Shvartsman, "Riemann surfaces" J. Soviet Math. , 14 : 1 (1980) pp. 985–1020 Itogi Nauk. i Tekhn. Algebra. Topol. Geom. , 16 (1978) pp. 191–245 MR0538254 Zbl 0445.30032 |
| [15a] | L. Bers, "Quasi-conformal mappings and Teichmüller's theorem" R. Nevanlinna (ed.) et al. (ed.) , Analytic functions , Princeton Univ. Press (1960) pp. 89–119 MR114898 |
| [15b] | L.V. Ahlfors, "The complex analytic structure of the space of closed Riemann surfaces" R. Nevanlinna (ed.) et al. (ed.) , Analytic functions , Princeton Univ. Press (1960) pp. 45–66 MR0124486 Zbl 0100.28903 |
| [15c] | L. Bers, "Spaces of Riemann surfaces" J.A. Todd (ed.) , Proc. Internat. Congress Mathematicians (Edinburgh, 1958) , Cambridge Univ. Press (1960) pp. 349–361 MR0124484 MR0111835 Zbl 0116.28803 Zbl 0106.28501 |
| [15d] | L. Bers, "Simultaneous uniformization" Bull. Amer. Math. Soc. , 66 (1960) pp. 94–97 MR0111834 Zbl 0090.05101 |
| [15e] | L. Bers, "Holomorphic differentials as functions of moduli" Bull. Amer. Math. Soc. , 67 (1961) pp. 206–210 MR0122989 Zbl 0102.06702 |
| [15f] | L. Ahlfors, "On quasiconformal mappings" J. d'Anal. Math. , 3 (1954) pp. 1–58; 207–208 MR0064875 Zbl 0057.06506 |
| [16a] | L. Bers, "Uniformization, moduli, and Kleinian groups" Bull. London Math. Soc. , 4 (1972) pp. 257–300 MR0348097 Zbl 0257.32012 |
| [16b] | L. Bers, "The moduli of Kleinian groups" Russian Math. Surveys , 29 : 2 (1974) pp. 88–102 Uspekhi Mat. Nauk , 29 : 2 (1974) pp. 86–102 MR0422691 |
| [17] | F. Klein, "Riemannschen Flächen" , Springer, reprint (1986) |
| [18] | H. Weyl, "The concept of a Riemann surface" , Addison-Wesley (1955) (Translated from German) MR1440406 MR0166351 |
| [19] | L.V. Ahlfors, L. Sario, "Riemann surfaces" , Princeton Univ. Press (1974) MR0667739 MR0712145 MR0279300 MR0204641 MR0130368 MR0124486 MR0114911 MR0093583 MR0083561 MR1565732 MR0090649 MR0055250 MR0054729 MR0054055 MR0043912 MR0036318 Zbl 0508.01017 Zbl 0445.30001 Zbl 0213.35602 Zbl 0146.30602 Zbl 0196.33801 Zbl 0100.28903 Zbl 0178.08201 Zbl 0114.28101 Zbl 0071.07502 Zbl 0066.32801 Zbl 0052.30503 Zbl 0050.08403 Zbl 0048.05905 Zbl 0048.05904 Zbl 0042.31603 Zbl 0041.41102 Zbl 0029.25802 Zbl 0018.26202 Zbl 0015.36001 Zbl 0006.26204 |
| [20] | A. Pfluger, "Theorie der Riemannschen Flächen" , Springer (1957) MR0084031 Zbl 0077.07803 |
| [21] | L. Sario, M. Nakai, "Classification theory of Riemann surfaces" , Springer (1970) MR0264064 Zbl 0199.40603 |
| [22] | M. Heins, "Hardy classes on Riemann surfaces" , Springer (1969) MR0247069 Zbl 0176.03001 |
| [23] | R.C. Gunning, "Lectures on Riemann surfaces" , Princeton Univ. Press (1966) MR0207977 Zbl 0175.36801 |
| [24] | R.C. Gunning, "Lectures on Riemann surfaces: Jacobi varieties" , Princeton Univ. Press (1972) MR0357407 Zbl 0387.32008 |
| [25] | O. Forster, "Lectures on Riemann surfaces" , Springer (1981) (Translated from German) MR0648106 Zbl 0475.30002 |
Comments
For the generalization to "Riemann surfaces over $\mathbf C^n$" see, e.g., [a6] and Riemannian domain.
References
| [a1] | P.A. Griffiths, J.E. Harris, "Principles of algebraic geometry" , Wiley (Interscience) (1978) MR0507725 Zbl 0408.14001 |
| [a2] | P. Griffiths, "Introduction to algebraic curves" , Amer. Math. Soc. (1989) MR1013999 Zbl 0696.14012 |
| [a3] | H.M. Farkas, I. Kra, "Riemann surfaces" , Springer (1980) pp. Sect. III.6 MR0583745 Zbl 0475.30001 |
| [a4] | H. Behnke, F. Sommer, "Theorie der analytischen Funktionen einer komplexen Veränderlichen" , Springer (1955) MR0073682 Zbl 0065.06102 |
| [a5] | H. Cohn, "Conformal mapping on Riemann surfaces" , Dover, reprint (1980) MR0594937 Zbl 0493.30001 |
| [a6] | H. Behnke, P. Thullen, "Theorie der Funktionen meherer komplexer Veränderlichen" , Springer (1970) pp. Chapt. VI (Elraged & Revised Edition. Original: 1934) |
| [a7] | W. Osgood, "Lehrbuch der Funktionentheorie" , 1–2 , Chelsea, reprint (1965) MR0196039 MR0196038 Zbl 0005.29904 Zbl 58.0390.04 Zbl 54.0326.10 Zbl 55.0171.02 Zbl 50.0209.04 Zbl 43.0476.02 Zbl 37.0409.02 Zbl 38.0412.01 |
Riemann surface. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Riemann_surface&oldid=23963