|
|
| (One intermediate revision by one other user not shown) |
| Line 1: |
Line 1: |
| | + | {{TEX|done}} |
| | ''of a graph'' | | ''of a graph'' |
| | | | |
| − | Suppose <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/o/o110/o110060/o1100601.png" /> is a (simple) [[Graph|graph]]. A matching in <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/o/o110/o110060/o1100602.png" /> is a set of pairwise-disjoint edges in <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/o/o110/o110060/o1100603.png" />. A one-factor or spanning matching is a set of edges such that every vertex of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/o/o110/o110060/o1100604.png" /> occurs in exactly one edge. | + | Suppose $G$ is a (simple) [[Graph|graph]]. A matching in $G$ is a set of pairwise-disjoint edges in $G$. A one-factor or spanning matching is a set of edges such that every vertex of $G$ occurs in exactly one edge. |
| | | | |
| − | Not every graph <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/o/o110/o110060/o1100605.png" /> has a one-factor. One obvious necessary condition is that <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/o/o110/o110060/o1100606.png" /> has no connected component with an odd number of vertices. However this is not a sufficient condition. The smallest graph connected with an even number of vertices but no one-factor is: | + | Not every graph $G$ has a one-factor. One obvious necessary condition is that $G$ has no connected component with an odd number of vertices. However this is not a sufficient condition. The smallest graph connected with an even number of vertices but no one-factor is: |
| | | | |
| | <img style="border:1px solid;" src="https://www.encyclopediaofmath.org/legacyimages/common_img/o110060a.gif" /> | | <img style="border:1px solid;" src="https://www.encyclopediaofmath.org/legacyimages/common_img/o110060a.gif" /> |
| Line 9: |
Line 10: |
| | Figure: o110060a | | Figure: o110060a |
| | | | |
| − | One-factors were first studied by W.T. Tutte, who proved the following characterization. If <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/o/o110/o110060/o1100607.png" /> is any subset of the vertex set <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/o/o110/o110060/o1100608.png" /> of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/o/o110/o110060/o1100609.png" />, let <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/o/o110/o110060/o11006010.png" /> denote the graph constructed from <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/o/o110/o110060/o11006011.png" /> by deleting <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/o/o110/o110060/o11006012.png" /> and all edges touching members of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/o/o110/o110060/o11006013.png" />. The components of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/o/o110/o110060/o11006014.png" /> are odd or even according as they have an odd or even number of vertices. Write <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/o/o110/o110060/o11006015.png" /> for the number of odd components of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/o/o110/o110060/o11006016.png" />. | + | One-factors were first studied by W.T. Tutte, who proved the following characterization. If $W$ is any subset of the vertex set $V(G)$ of $G$, let $G-W$ denote the graph constructed from $G$ by deleting $W$ and all edges touching members of $W$. The components of $G-W$ are odd or even according as they have an odd or even number of vertices. Write $\phi(W)$ for the number of odd components of $G-W$. |
| | | | |
| − | Tutte's theorem [[#References|[a6]]]: <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/o/o110/o110060/o11006017.png" /> contains a one-factor if and only if <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/o/o110/o110060/o11006018.png" /> whenever <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/o/o110/o110060/o11006019.png" />. | + | Tutte's theorem [[#References|[a6]]]: $G$ contains a one-factor if and only if $\phi(W)\leq|W|$ whenever $W\leq V(G)$. |
| | | | |
| − | A consequence is that for <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/o/o110/o110060/o11006020.png" /> even, any regular graph of degree <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/o/o110/o110060/o11006021.png" /> on <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/o/o110/o110060/o11006022.png" /> vertices has a one-factor. | + | A consequence is that for $n$ even, any [[regular graph]] of degree $n-1$ on $2n$ vertices has a one-factor. |
| | | | |
| − | A bridge in a graph <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/o/o110/o110060/o11006023.png" /> is an edge whose deletion disconnects <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/o/o110/o110060/o11006024.png" />. | + | A bridge in a graph $G$ is an edge whose deletion disconnects $G$. |
| | | | |
| | Petersen's theorem [[#References|[a4]]]: A bridgeless cubic graph contains a one-factor. | | Petersen's theorem [[#References|[a4]]]: A bridgeless cubic graph contains a one-factor. |
| | | | |
| − | This has been generalized by T. Schönberger [[#References|[a5]]], who proved that every edge of a bridgeless cubic graph lies in a one-factor. C. Berge [[#References|[a1]]] and A.B. Cruse [[#References|[a3]]] proved another generalization. If <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/o/o110/o110060/o11006025.png" /> is any set of vertices of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/o/o110/o110060/o11006026.png" />, let <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/o/o110/o110060/o11006027.png" /> be the number of edges of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/o/o110/o110060/o11006028.png" /> with exactly one end-point in <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/o/o110/o110060/o11006029.png" />. | + | This has been generalized by T. Schönberger [[#References|[a5]]], who proved that every edge of a bridgeless cubic graph lies in a one-factor. C. Berge [[#References|[a1]]] and A.B. Cruse [[#References|[a3]]] proved another generalization. If $W$ is any set of vertices of $G$, let $z_G(W)$ be the number of edges of $G$ with exactly one end-point in $W$. |
| | | | |
| − | The Berge–Cruse theorem: If <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/o/o110/o110060/o11006030.png" /> is a regular graph of degree <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/o/o110/o110060/o11006031.png" /> with an even number of vertices, and if <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/o/o110/o110060/o11006032.png" /> for all odd-order subsets <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/o/o110/o110060/o11006033.png" /> of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/o/o110/o110060/o11006034.png" />, then each edge of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/o/o110/o110060/o11006035.png" /> belongs to some one-factor. | + | The Berge–Cruse theorem: If $G$ is a regular graph of degree $d$ with an even number of vertices, and if $z_G(W)\leq d-1$ for all odd-order subsets $W$ of $V(G)$, then each edge of $G$ belongs to some one-factor. |
| | | | |
| | Consequences are [[#References|[a3]]]: | | Consequences are [[#References|[a3]]]: |
| | | | |
| − | 1) if <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/o/o110/o110060/o11006036.png" /> is a regular graph of degree <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/o/o110/o110060/o11006037.png" /> with <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/o/o110/o110060/o11006038.png" /> vertices and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/o/o110/o110060/o11006039.png" /> (<img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/o/o110/o110060/o11006040.png" /> odd) or <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/o/o110/o110060/o11006041.png" /> (<img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/o/o110/o110060/o11006042.png" /> even), then every edge of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/o/o110/o110060/o11006043.png" /> belongs to some one-factor; | + | 1) if $G$ is a regular graph of degree $d$ with $2m$ vertices and $d\geq m$ ($m$ odd) or $d\geq m-1$ ($m$ even), then every edge of $G$ belongs to some one-factor; |
| | | | |
| − | 2) if <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/o/o110/o110060/o11006044.png" /> is a regular graph of valency <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/o/o110/o110060/o11006045.png" /> with <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/o/o110/o110060/o11006046.png" /> vertices and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/o/o110/o110060/o11006047.png" />, then <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/o/o110/o110060/o11006048.png" /> contains at least | + | 2) if $G$ is a regular graph of valency $d$ with $m$ vertices and $d\geq m\geq2$, then $G$ contains at least |
| | | | |
| − | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/o/o110/o110060/o11006049.png" /></td> </tr></table>
| + | $$d-m+2\left\lfloor\frac{5(m+5)}{112}\right\rfloor$$ |
| | | | |
| | disjoint one-factors. | | disjoint one-factors. |
of a graph
Suppose $G$ is a (simple) graph. A matching in $G$ is a set of pairwise-disjoint edges in $G$. A one-factor or spanning matching is a set of edges such that every vertex of $G$ occurs in exactly one edge.
Not every graph $G$ has a one-factor. One obvious necessary condition is that $G$ has no connected component with an odd number of vertices. However this is not a sufficient condition. The smallest graph connected with an even number of vertices but no one-factor is:
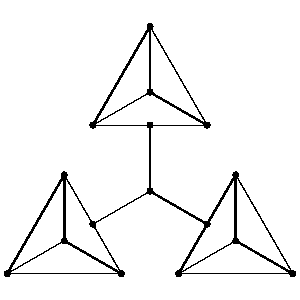
Figure: o110060a
One-factors were first studied by W.T. Tutte, who proved the following characterization. If $W$ is any subset of the vertex set $V(G)$ of $G$, let $G-W$ denote the graph constructed from $G$ by deleting $W$ and all edges touching members of $W$. The components of $G-W$ are odd or even according as they have an odd or even number of vertices. Write $\phi(W)$ for the number of odd components of $G-W$.
Tutte's theorem [a6]: $G$ contains a one-factor if and only if $\phi(W)\leq|W|$ whenever $W\leq V(G)$.
A consequence is that for $n$ even, any regular graph of degree $n-1$ on $2n$ vertices has a one-factor.
A bridge in a graph $G$ is an edge whose deletion disconnects $G$.
Petersen's theorem [a4]: A bridgeless cubic graph contains a one-factor.
This has been generalized by T. Schönberger [a5], who proved that every edge of a bridgeless cubic graph lies in a one-factor. C. Berge [a1] and A.B. Cruse [a3] proved another generalization. If $W$ is any set of vertices of $G$, let $z_G(W)$ be the number of edges of $G$ with exactly one end-point in $W$.
The Berge–Cruse theorem: If $G$ is a regular graph of degree $d$ with an even number of vertices, and if $z_G(W)\leq d-1$ for all odd-order subsets $W$ of $V(G)$, then each edge of $G$ belongs to some one-factor.
Consequences are [a3]:
1) if $G$ is a regular graph of degree $d$ with $2m$ vertices and $d\geq m$ ($m$ odd) or $d\geq m-1$ ($m$ even), then every edge of $G$ belongs to some one-factor;
2) if $G$ is a regular graph of valency $d$ with $m$ vertices and $d\geq m\geq2$, then $G$ contains at least
$$d-m+2\left\lfloor\frac{5(m+5)}{112}\right\rfloor$$
disjoint one-factors.
A number of results have been proved concerning whether a graph of a certain description (usually a quite sparse graph) contains a one-factor.
Important references include [a2], and [a7].
References
| [a1] | C. Berge, "Graphs and hypergraphs" , North-Holland (1973) (Translated from French) |
| [a2] | J. Bosák, "Decomposition of graphs" , Kluwer Acad. Publ. (1990) |
| [a3] | A.B. Cruse, "A note on one-factors in certain regular multigraphs" Discrete Math. , 18 (1977) pp. 213–216 |
| [a4] | J. Petersen, "Die Theorie der regulären Graphes" Acta Math. , 15 (1981) pp. 193–220 |
| [a5] | T. Schönberger, "Ein Beweis des Peterschen Graphensatzes" Acta Sci. Math. Szeged , 7 (1934) pp. 51–57 |
| [a6] | W.T. Tutte, "The factorizations of linear graphs" J. London Math. Soc. , 22 (1947) pp. 459–474 |
| [a7] | W.D. Wallis, "One-factorizations" , Kluwer Acad. Publ. (1997) |
