One-factor
of a graph
Suppose 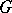 is a (simple) graph. A matching in
is a (simple) graph. A matching in 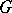 is a set of pairwise-disjoint edges in
is a set of pairwise-disjoint edges in 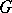 . A one-factor or spanning matching is a set of edges such that every vertex of
. A one-factor or spanning matching is a set of edges such that every vertex of 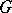 occurs in exactly one edge.
occurs in exactly one edge.
Not every graph 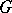 has a one-factor. One obvious necessary condition is that
has a one-factor. One obvious necessary condition is that 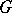 has no connected component with an odd number of vertices. However this is not a sufficient condition. The smallest graph connected with an even number of vertices but no one-factor is:
has no connected component with an odd number of vertices. However this is not a sufficient condition. The smallest graph connected with an even number of vertices but no one-factor is:
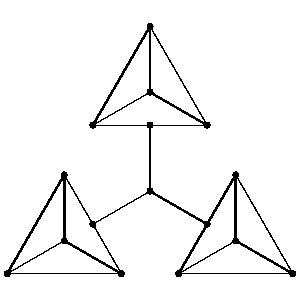
Figure: o110060a
One-factors were first studied by W.T. Tutte, who proved the following characterization. If 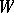 is any subset of the vertex set
is any subset of the vertex set 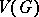 of
of 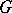 , let
, let 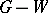 denote the graph constructed from
denote the graph constructed from 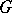 by deleting
by deleting 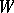 and all edges touching members of
and all edges touching members of 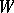 . The components of
. The components of 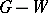 are odd or even according as they have an odd or even number of vertices. Write
are odd or even according as they have an odd or even number of vertices. Write 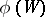 for the number of odd components of
for the number of odd components of 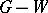 .
.
Tutte's theorem [a6]: 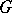 contains a one-factor if and only if
contains a one-factor if and only if 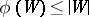 whenever
whenever 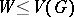 .
.
A consequence is that for  even, any regular graph of degree
even, any regular graph of degree 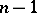 on
on 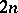 vertices has a one-factor.
vertices has a one-factor.
A bridge in a graph 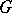 is an edge whose deletion disconnects
is an edge whose deletion disconnects 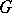 .
.
Petersen's theorem [a4]: A bridgeless cubic graph contains a one-factor.
This has been generalized by T. Schönberger [a5], who proved that every edge of a bridgeless cubic graph lies in a one-factor. C. Berge [a1] and A.B. Cruse [a3] proved another generalization. If 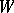 is any set of vertices of
is any set of vertices of 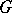 , let
, let 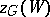 be the number of edges of
be the number of edges of 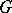 with exactly one end-point in
with exactly one end-point in 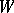 .
.
The Berge–Cruse theorem: If 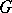 is a regular graph of degree
is a regular graph of degree 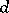 with an even number of vertices, and if
with an even number of vertices, and if 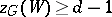 for all odd-order subsets
for all odd-order subsets 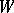 of
of 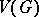 , then each edge of
, then each edge of 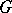 belongs to some one-factor.
belongs to some one-factor.
Consequences are [a3]:
1) if 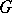 is a regular graph of degree
is a regular graph of degree 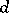 with
with 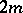 vertices and
vertices and 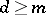 (
(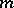 odd) or
odd) or 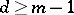 (
(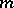 even), then every edge of
even), then every edge of 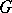 belongs to some one-factor;
belongs to some one-factor;
2) if 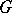 is a regular graph of valency
is a regular graph of valency 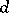 with
with 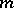 vertices and
vertices and 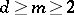 , then
, then 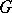 contains at least
contains at least
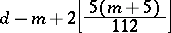 |
disjoint one-factors.
A number of results have been proved concerning whether a graph of a certain description (usually a quite sparse graph) contains a one-factor.
Important references include [a2], and [a7].
References
| [a1] | C. Berge, "Graphs and hypergraphs" , North-Holland (1973) (Translated from French) |
| [a2] | J. Bosák, "Decomposition of graphs" , Kluwer Acad. Publ. (1990) |
| [a3] | A.B. Cruse, "A note on one-factors in certain regular multigraphs" Discrete Math. , 18 (1977) pp. 213–216 |
| [a4] | J. Petersen, "Die Theorie der regulären Graphes" Acta Math. , 15 (1981) pp. 193–220 |
| [a5] | T. Schönberger, "Ein Beweis des Peterschen Graphensatzes" Acta Sci. Math. Szeged , 7 (1934) pp. 51–57 |
| [a6] | W.T. Tutte, "The factorizations of linear graphs" J. London Math. Soc. , 22 (1947) pp. 459–474 |
| [a7] | W.D. Wallis, "One-factorizations" , Kluwer Acad. Publ. (1997) |
One-factor. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=One-factor&oldid=18817