Difference between revisions of "Yang-Baxter operators"
m (link) |
m (Automatically changed introduction) |
||
| (One intermediate revision by the same user not shown) | |||
| Line 1: | Line 1: | ||
| + | <!--This article has been texified automatically. Since there was no Nroff source code for this article, | ||
| + | the semi-automatic procedure described at https://encyclopediaofmath.org/wiki/User:Maximilian_Janisch/latexlist | ||
| + | was used. | ||
| + | If the TeX and formula formatting is correct and if all png images have been replaced by TeX code, please remove this message and the {{TEX|semi-auto}} category. | ||
| + | |||
| + | Out of 149 formulas, 142 were replaced by TEX code.--> | ||
| + | |||
| + | {{TEX|semi-auto}}{{TEX|part}} | ||
In their most familiar form, Yang–Baxter operators are certain invertible linear endomorphisms which have applications to physics and topology. In physics these operators often provide solutions to the quantum [[Yang–Baxter equation|Yang–Baxter equation]], an equation which has its roots in statistical mechanics [[#References|[a30]]], [[#References|[a7]]], [[#References|[a28]]], [[#References|[a31]]], [[#References|[a35]]] (cf. also [[Statistical mechanics, mathematical problems in|Statistical mechanics, mathematical problems in]]). In topology quite often they can be used to construct invariants of knots, links or three-dimensional manifolds (cf. also [[Knot theory|Knot theory]]; [[Link|Link]]; [[Three-dimensional manifold|Three-dimensional manifold]]); cf. [[#References|[a30]]], [[#References|[a17]]], [[#References|[a18]]], [[#References|[a26]]], [[#References|[a27]]], [[#References|[a32]]], [[#References|[a33]]]. | In their most familiar form, Yang–Baxter operators are certain invertible linear endomorphisms which have applications to physics and topology. In physics these operators often provide solutions to the quantum [[Yang–Baxter equation|Yang–Baxter equation]], an equation which has its roots in statistical mechanics [[#References|[a30]]], [[#References|[a7]]], [[#References|[a28]]], [[#References|[a31]]], [[#References|[a35]]] (cf. also [[Statistical mechanics, mathematical problems in|Statistical mechanics, mathematical problems in]]). In topology quite often they can be used to construct invariants of knots, links or three-dimensional manifolds (cf. also [[Knot theory|Knot theory]]; [[Link|Link]]; [[Three-dimensional manifold|Three-dimensional manifold]]); cf. [[#References|[a30]]], [[#References|[a17]]], [[#References|[a18]]], [[#References|[a26]]], [[#References|[a27]]], [[#References|[a32]]], [[#References|[a33]]]. | ||
Closely related to the quantum Yang–Baxter equation is the braid equation. There are natural categorical structures associated with the braid and quantum Yang–Baxter equations which play an important role in [[Quantum groups|quantum groups]] and their applications [[#References|[a21]]], [[#References|[a23]]], [[#References|[a5]]], [[#References|[a34]]]. | Closely related to the quantum Yang–Baxter equation is the braid equation. There are natural categorical structures associated with the braid and quantum Yang–Baxter equations which play an important role in [[Quantum groups|quantum groups]] and their applications [[#References|[a21]]], [[#References|[a23]]], [[#References|[a5]]], [[#References|[a34]]]. | ||
| − | Yang–Baxter operators in the [[Category|category]] | + | Yang–Baxter operators in the [[Category|category]] $\square _ { k }\operatorname {Mod}$ of left modules over a [[Commutative ring|commutative ring]] $k$ are certain $k$-linear mappings $R : V \otimes _ { k } V \rightarrow V \otimes _ { k } V$. Let $R _ { 12 } = R \otimes _ { k } 1$, $R _ { 23 } = 1 \otimes _ { k } R$ and $R _ { 13 } = ( 1 \otimes _ { k } \tau _ { V , V } ) ( R \otimes _ { k } 1 ) ( 1 \otimes _ { k } \tau _ { V , V } )$, where $\tau _ { U , V } : U \otimes _ { k } V \rightarrow V \otimes _ { k } U$ is the "twist" mapping defined for $k$-modules $U$ and $V$ by $\tau_{ U , V } ( u \otimes v ) = v \otimes u$ for all $u \in U$ and $v \in V$. Then $R$ satisfies the quantum Yang–Baxter equation in $\square _ { k }\operatorname {Mod}$ if |
| − | + | \begin{equation} \tag{a1} R _ { 12 } R _ { 13 } R _ { 23 } = R _ { 23 } R _ { 13 } R _ { 12 }. \end{equation} | |
| − | Note that | + | Note that $R$ satisfies (a1) if and only if $B = \tau _ { V , V } R$ satisfies the braid equation in $\square _ { k }\operatorname {Mod}$, which is |
| − | + | \begin{equation} \tag{a2} B _ { 12 } B _ { 23 } B _ { 12 } = B _ { 23 } B _ { 12 } B _ { 23 }. \end{equation} | |
| − | If | + | If $R$ is invertible and satisfies (a2), that is, $R _ { 12 } R _ { 23 } R _ { 12 } = R _ { 23 } R _ { 12 } R _ { 23 }$, then $R$ is a Yang–Baxter operator in $\square _ { k }\operatorname {Mod}$ (see [[#References|[a5]]]). There are other formulations of the notion of Yang–Baxter operator in the context of modules; see, e.g., [[#References|[a8]]] and [[#References|[a9]]]. |
| − | Observe that the quantum Yang–Baxter and braid equations have natural formulations in any category | + | Observe that the quantum Yang–Baxter and braid equations have natural formulations in any category $\mathcal{C}$ with a suitable notion of tensor product and in which the tensor product of morphisms is defined [[#References|[a16]]], [[#References|[a20]]], [[#References|[a34]]]. The notion of quantum Yang–Baxter operator thus has a natural generalization to categories $\mathcal{C}$ with such additional structure; see, e.g., [[#References|[a16]]], [[#References|[a5]]]. |
| − | A good source of solutions to (a1) in | + | A good source of solutions to (a1) in $\square _ { k }\operatorname {Mod}$ are certain elements $R = \sum _ { s = 1 } ^ { n } a _ { s } \otimes b _ { s } \in A \otimes _ { k } A$, where $A$ is an [[Algebra|algebra]] over $k$. For $R \in A \otimes _ { k } A$ and a $k$-module $V$, let $R _ { V } : V \otimes _ { k } V \rightarrow V \otimes _ { k } V$ be defined by $R _ { V } ( u \otimes v ) = R \cdot ( u \otimes v )$ for all $u , v \in V$, where $V \otimes _ { k } V$ is regarded as a left $A \otimes _ { k } A$-module under component multiplication. Then $R _ { V }$ is a solution to (a1) for all left $k$-modules $V$ if and only if |
| − | <table class="eq" style="width:100%;"> <tr><td | + | <table class="eq" style="width:100%;"> <tr><td style="width:94%;text-align:center;" valign="top"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/y/y120/y120010/y12001044.png"/></td> <td style="width:5%;text-align:right;" valign="top">(a3)</td></tr></table> |
| − | When | + | When $A = M _ { n } ( k )$ is the algebra of $( n \times n )$-matrices over $k$, then an $R \in A \otimes _ { k } A$ which satisfies (a1), or equivalently (a3), is called an $R$-matrix. Suppose that $A = M _ { n } ( k )$ and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/y/y120/y120010/y12001052.png"/>, where $r _ { t \text{l}} ^ { s k } \in k $ and $\{ E _ { t } ^ { s } \} _ { 1 \leq s , t \leq n}$ is the standard basis for $A$. Then (a3) is equivalent to |
| − | <table class="eq" style="width:100%;"> <tr><td | + | <table class="eq" style="width:100%;"> <tr><td style="width:94%;text-align:center;" valign="top"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/y/y120/y120010/y12001056.png"/></td> <td style="width:5%;text-align:right;" valign="top">(a4)</td></tr></table> |
| − | for all | + | for all $1 \leq p , q , r , a , b , c \leq n$, which is probably the most familiar form of the quantum Yang–Baxter equation. Ordinarily, (a4) is written using the Einstein [[summation convention]], that is, summation signs are omitted with the understanding that indices that appear as upper and lower indices are summed over their full range of values. |
| − | Certain | + | Certain $k$-algebras $A$ with an $R \in A \otimes _ { k } A$ which satisfies (a1) can be used to construct invariants. Quasi-triangular Hopf algebras, in particular quantum algebras (cf. also [[Quasi-triangular Hopf algebra|Quasi-triangular Hopf algebra]]), give rise to regular isotopy invariants of $1$-$1$ tangles. Ribbon Hopf algebras give rise to regular isotopy invariants of knots and links, and under mild restrictions they give rise to invariants of three-dimensional manifolds. Let $k$ be a field. In this case a finite-dimensional [[Hopf algebra|Hopf algebra]] $A$ over $k$ is closely linked to these structures. The Hopf algebra $A$ is a subHopf algebra of the quantum double $D ( A )$ of $A$, which is a quasi-triangular Hopf algebra [[#References|[a1]]]. Every finite-dimensional quasi-triangular Hopf algebra over $k$ is a subHopf algebra of a ribbon Hopf algebra; in particular, $A$ is a subHopf algebra of a ribbon Hopf algebra [[#References|[a6]]]. |
| − | The classification of | + | The classification of $R$-matrices seems to be a very daunting task, and most work to date (1998) has involved symbolic computation. Suppose that $k$ is the field of complex numbers. Then the $R$-matrices are completely classified in the $n = 2$ case [[#References|[a13]]] and the classification of one basic family is known in the $n = 3$ case [[#References|[a14]]]. |
| − | Some of the more important examples of | + | Some of the more important examples of $R$-matrices, those related to the quantized enveloping algebras, are formal infinite sums or belong to a completed tensor product. See [[#References|[a4]]], [[#References|[a1]]] for discussion of this important part of the theory. |
| − | There is a category | + | There is a category $\square _ { A } ^ { A } \mathcal{C}$ with a pre-braiding structure, defined and studied in [[#References|[a34]]], associated to a bi-algebra $A$ over $k$ which gives rise to Yang–Baxter operators. Here, the formal variant $\square _ { A } \mathcal{C} ^ { A }$ is considered, whose objects are left $A$-modules and right $A$-comodules $V$ which satisfy the condition |
| − | <table class="eq" style="width:100%;"> <tr><td | + | <table class="eq" style="width:100%;"> <tr><td style="width:94%;text-align:center;" valign="top"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/y/y120/y120010/y12001084.png"/></td> </tr></table> |
| − | for all | + | for all $a \in A$ and $v \in V$, where $\rho ( v ) = v ^ { ( 1 ) } \otimes v ^ { ( 2 ) } \in V \otimes _ { k } A$ denotes the [[Coproduct|coproduct]] $\rho$ applied to $v \in V$. For an object $V$ of $\square _ { A } \mathcal{C} ^ { A }$, define $\mathcal{R} _ { V } : V \otimes _ { k } V \rightarrow V \otimes _ { k } V$ by $\mathcal{R} _ { V } ( u \otimes v ) = u ^ { \{ 1 \} } \otimes u ^ { ( 2 ) } . v$ for all $u , v \in V$. Then $\mathcal{R} _ { V }$ satisfies (a1). The pre-braiding structure on $\square _ { A } \mathcal{C} ^ { A }$ is the collection of morphisms of the form $\sigma _ { U , V } : U \otimes _ { k } V \rightarrow V \otimes _ { k } U$ which are defined for all pairs of objects $U$, $V$ by $\sigma_{ U , V} ( u \otimes v ) = u ^ { ( 2 ) } . v \otimes u ^ { ( 1 ) }$ for all $u \in U$ and $v \in V$. Observe that $\sigma_{ V , V } = \tau_{ V , V} R _ { V }$ is a solution to the braid equation (a2). When $A$ is a [[Hopf algebra|Hopf algebra]], the morphism $\sigma_{ U, V}$ is invertible, and the collection of all $\sigma_{ U, V}$ is referred to as a braiding structure. When $k$ is a field and $A$ is a finite-dimensional Hopf algebra over $k$, the category $\square _ { D(A) } \mathcal{C}^{D ( A )}$ can be identified with $\square _{D(A)} \operatorname{Mod}$, the category of left modules of the quantum double [[#References|[a23]]]. |
| − | The FRT construction of [[#References|[a11]]], [[#References|[a10]]] has an interesting interpretation in light of the preceding paragraph. Suppose that | + | The FRT construction of [[#References|[a11]]], [[#References|[a10]]] has an interesting interpretation in light of the preceding paragraph. Suppose that $k$ is a field and $R : V \otimes _ { k } V \rightarrow V \otimes _ { k } V$ is a solution to (a1), where $V$ is a finite-dimensional [[Vector space|vector space]] over $k$. The FRT construction $A ( R )$ is a certain bi-algebra over $k$ associated with $R$. There is a natural way of turning $V$ into an object of $\square _ { A ( R ) } {\cal C} ^ { A ( R) }$ such that $R = \mathcal{R} _ { \mathcal{V} }$, described in [[#References|[a24]]]. For a universal description of the FRT construction associated with certain Yang–Baxter operators, see [[#References|[a5]]], [[#References|[a21]]]. See also [[#References|[a8]]] for a discussion of algebras associated with Yang–Baxter operators. |
| − | There is a certain quotient | + | There is a certain quotient $\widetilde { A ( R )}$ of $A ( R )$ which is more closely tied to $R$ from a computational point of view. If $V \neq ( 0 )$, then it is never the case that $A ( R )$ is a Hopf algebra, whereas $\widetilde { A ( R )}$ may very well be a Hopf algebra [[#References|[a25]]]. Determining new families of solutions to (a1) of the type described in the preceding paragraph may very well involve using a combination of bi-algebra techniques involving $\widetilde { A ( R )}$ and computer methods [[#References|[a3]]], [[#References|[a25]]]. |
| − | There are parametrized versions of (a1), and hence parametrized versions of Yang–Baxter operators. Let | + | There are parametrized versions of (a1), and hence parametrized versions of Yang–Baxter operators. Let $X$ be a set, $R : X \rightarrow \operatorname { End } _ { k } ( V \otimes _ { k } V )$ be a function and suppose that $Z \subseteq X \times X$ is a non-empty subset with a (multiplication) mapping $Z \rightarrow X$. Then $R$ satisfies the $1$-parameter quantum Yang–Baxter equation if |
| − | + | \begin{equation*} R ( x ) _ { 12 } R ( x y ) _ { 13 } R ( y ) _ { 23 } = R ( y ) _ { 23 } R ( x y ) _ { 13 } R ( x ) _ { 12 } \end{equation*} | |
| − | holds for all | + | holds for all $( x , y ) \in Z$. There is an FRT construction for $1$-parameter families [[#References|[a3]]]. A $2$-parameter family of solutions to the quantum Yang–Baxter equation is a function $R : X \times X \rightarrow \operatorname { End } _ { k } ( V \otimes _ { k } V )$ which satisfies |
| − | + | \begin{equation*} R ( x , y ) _ { 12 } R ( x , z ) _ { 13 } R ( y , z ) _ { 23 } = \end{equation*} | |
| − | + | \begin{equation*} = R ( y , z ) _ { 23 } R ( x , z ) _ { 13 } R ( x , y ) _ { 12 } \end{equation*} | |
| − | for all | + | for all $x , y , z \in X$. For examples and discussion, see [[#References|[a1]]], [[#References|[a12]]], [[#References|[a11]]], [[#References|[a15]]], [[#References|[a19]]]. |
====References==== | ====References==== | ||
| − | <table>< | + | <table><tr><td valign="top">[a1]</td> <td valign="top"> V.G. Drinfel'd, "Quantum groups" , ''Proc. Internat. Congress Mathematicians Berkeley, California, (1987)'' , Amer. Math. Soc. (1988) pp. 798–820</td></tr><tr><td valign="top">[a2]</td> <td valign="top"> C. Kassel, "Quantum groups" , ''Graduate Texts Math.'' , '''155''' , Springer (1995)</td></tr><tr><td valign="top">[a3]</td> <td valign="top"> L.A. Lambe, D.E. Radford, "Introduction to the quantum Yang–Baxter equation and quantum groups: An algebraic approach" , Kluwer Acad. Publ. (1997)</td></tr><tr><td valign="top">[a4]</td> <td valign="top"> V. Chari, A. Pressley, "A guide to quantum groups" , Cambridge Univ. Press (1994) (Corrected reprint: 1995)</td></tr><tr><td valign="top">[a5]</td> <td valign="top"> P. Schauenburg, "On coquasitriangular Hopf algebras and the quantum Yang–Baxter equation" , ''Algebra Berichte'' , '''67''' , R. Fischer (1992)</td></tr><tr><td valign="top">[a6]</td> <td valign="top"> N.Yu. Reshetikhin, V.G. Turaev, "Ribbon graphs and their invariants derived from quantum groups" ''Comm. Math. Phys.'' , '''127''' (1990) pp. 1–26</td></tr><tr><td valign="top">[a7]</td> <td valign="top"> R. Baxter, "Exactly solved models in stastistical mechanics" , Acad. Press (1982)</td></tr><tr><td valign="top">[a8]</td> <td valign="top"> Yu.I. Manin, "Quantum groups and noncommutative geometry" ''Centre de Recherche Math. Univ. Montreal'' (1988)</td></tr><tr><td valign="top">[a9]</td> <td valign="top"> V.G. Turaev, "The Yang–Baxter equation and invariants of links" ''Invent. Math.'' , '''92''' : 3 (1988) pp. 527–553</td></tr><tr><td valign="top">[a10]</td> <td valign="top"> L.D. Faddeev, N.Yu. Reshetikhin, L.A. Takhtadzhan, "Quantization of Lie groups and Lie algebras" ''Leningrad Math. J.'' , '''1''' (1990) pp. 193–225 ''Algebra Anal.'' , '''1''' (1989) pp. 178–206</td></tr><tr><td valign="top">[a11]</td> <td valign="top"> L.D. Faddeev, N.Yu. Reshetikhin, L.A. Takhtadzhan, "Quantum groups" , ''Braid group, knot theory and statistical mechanics'' , ''Adv. Ser. Math. Phys.'' , '''9''' , World Sci. (1989) pp. 97–110</td></tr><tr><td valign="top">[a12]</td> <td valign="top"> L.D. Faddeev, N.Yu. Reshetikhin, L.A. Takhtadzhan, "Quantization of Lie groups and Lie algebras" , ''Algebraic analysis, Papers Dedicated to Prof. Mikio Sato on the Occasion of his Sixtieth Birthday'' , '''I''' , Acad. Press (1988) pp. 129–139</td></tr><tr><td valign="top">[a13]</td> <td valign="top"> J. Hietarinta, "Solving the two-dimensional constant quantum Yang-Baxter equation" ''J. Math. Phys.'' , '''34''' (1993) pp. 1725–1756</td></tr><tr><td valign="top">[a14]</td> <td valign="top"> J. Hietarinta, "The upper triangular solutions to the three-state constant quantum Yang-Baxter equation" ''J. Phys. A'' , '''26''' (1993) pp. 7077–7095</td></tr><tr><td valign="top">[a15]</td> <td valign="top"> M. Jimbo, "A $q$-difference analogue of $U ( g )$ and the Yang–Baxter equation" ''Lett. Math. Phys.'' , '''10''' (1985) pp. 63–69</td></tr><tr><td valign="top">[a16]</td> <td valign="top"> A. Joyal, R. Street, "Braided tensor categories" ''Adv. Math.'' , '''102''' (1993) pp. 20–78</td></tr><tr><td valign="top">[a17]</td> <td valign="top"> L.H. Kauffman, "Knots and physics" , ''Ser. Knots and Everything'' , '''1''' , World Sci. (1991)</td></tr><tr><td valign="top">[a18]</td> <td valign="top"> L.H. Kauffman, S. Lins, "Temperley–Lieb recoupling theory and invariants of $3$-manifolds" , ''Ann. Math. Studies'' , '''134''' , Princeton Univ. Press (1994)</td></tr><tr><td valign="top">[a19]</td> <td valign="top"> P.P. Kulish, N.Yu. Reshetikhin, E.K. Sklyanin, "Yang–Baxter equation and representation theory: I" ''Lett. Math. Phys.'' , '''5''' (1981) pp. 393–403</td></tr><tr><td valign="top">[a20]</td> <td valign="top"> L.A. Lambe, D.E. Radford, "Algebraic aspects of the quantum Yang-Baxter equation" ''J. Algebra'' , '''154''' (1993) pp. 228–288</td></tr><tr><td valign="top">[a21]</td> <td valign="top"> R.G. Larson, J. Towber, "Two dual classes of bialgebras related to the concepts of `quantum groups' and `quantum lie algebras'" ''Commun. Algebra'' , '''19''' (1991) pp. 3295–3345</td></tr><tr><td valign="top">[a22]</td> <td valign="top"> S. Majid, "Foundations of quantum group theory" , Cambridge Univ. Press (1995)</td></tr><tr><td valign="top">[a23]</td> <td valign="top"> S. Majid, "Doubles of quasi triangular Hopf algebras" ''Commun. Algebra'' , '''19''' (1991) pp. 3061–3073</td></tr><tr><td valign="top">[a24]</td> <td valign="top"> D.E. Radford, "Solutions to the quantum Yang–Baxter equation and the Drinfel'd double" ''J. Algebra'' , '''161''' (1993) pp. 20–32</td></tr><tr><td valign="top">[a25]</td> <td valign="top"> D.E. Radford, "Solutions to the quantum Yang–Baxter equation arising from pointed bi-algebras" ''Trans. Amer. Math. Soc.'' , '''343''' (1994) pp. 455–477</td></tr><tr><td valign="top">[a26]</td> <td valign="top"> N. Reshetikhin, "Invariants of links and $3$-manifolds related to quantum groups" , ''Proc. Internat. Congr. Math., Kyoto, August, 21-29, 1990'' , '''II''' , Springer (1991) pp. 1373–1375</td></tr><tr><td valign="top">[a27]</td> <td valign="top"> N.Yu. Reshetikhin, V.G. Turaev, "Invariants of $3$-manifolds via link polynomials and quantum groups" ''Invent. Math.'' , '''103''' (1991) pp. 547–597</td></tr><tr><td valign="top">[a28]</td> <td valign="top"> G.M. D'Ariano, A. Montorsi, M.G. Rasetti, "Integrable systems in statistical mechanics" , ''Ser. Adv. Statist. Mech.'' , '''1''' , World Sci. (1985)</td></tr><tr><td valign="top">[a29]</td> <td valign="top"> S. Shnider, S. Sternberg, "Quantum groups. From coalgebras to Drinfel'd algebras. A guided tour" , ''Graduate Texts Math. Phys.'' , '''II''' , Internat. Press (1993)</td></tr><tr><td valign="top">[a30]</td> <td valign="top"> Y. Akutsu, T. Deguchi, M. Wadati, "Exactly solvable models and knot theory" ''Physics Reports. A Review Section of Physics Lett.'' , '''180''' (1989) pp. 247–332</td></tr><tr><td valign="top">[a31]</td> <td valign="top"> C.N. Yang, "Some exact results for the many-body problem in one dimension with repulsive delta-function interaction" ''Phys. Rev. Lett.'' , '''19''' (1967) pp. 1312–1315</td></tr><tr><td valign="top">[a32]</td> <td valign="top"> C.N. Yang, M.L. Ge, "Braid group, knot theory and statistical mechanics" , ''Adv. Ser. Math. Phys.'' , '''9''' , World Sci. (1989)</td></tr><tr><td valign="top">[a33]</td> <td valign="top"> C.N. Yang, M.L. Ge, "Braid group, knot theory and statistical mechanics, II" , ''Adv. Ser. Math. Phys.'' , '''17''' , World Sci. (1994)</td></tr><tr><td valign="top">[a34]</td> <td valign="top"> D.N. Yetter, "Quantum groups and representations of monoidal categories" ''Math. Proc. Cambridge Philos. Soc.'' , '''108''' (1990) pp. 261–290</td></tr><tr><td valign="top">[a35]</td> <td valign="top"> A.B. Zamolodchikov, A.B. Zamolodchikov, "Factorized $S$-matrices in two dimensions as the exact solutions of certain relativistic quantum field theory models" ''Ann. Phys.'' , '''120''' (1975) pp. 253–291</td></tr></table> |
Latest revision as of 17:45, 1 July 2020
In their most familiar form, Yang–Baxter operators are certain invertible linear endomorphisms which have applications to physics and topology. In physics these operators often provide solutions to the quantum Yang–Baxter equation, an equation which has its roots in statistical mechanics [a30], [a7], [a28], [a31], [a35] (cf. also Statistical mechanics, mathematical problems in). In topology quite often they can be used to construct invariants of knots, links or three-dimensional manifolds (cf. also Knot theory; Link; Three-dimensional manifold); cf. [a30], [a17], [a18], [a26], [a27], [a32], [a33].
Closely related to the quantum Yang–Baxter equation is the braid equation. There are natural categorical structures associated with the braid and quantum Yang–Baxter equations which play an important role in quantum groups and their applications [a21], [a23], [a5], [a34].
Yang–Baxter operators in the category $\square _ { k }\operatorname {Mod}$ of left modules over a commutative ring $k$ are certain $k$-linear mappings $R : V \otimes _ { k } V \rightarrow V \otimes _ { k } V$. Let $R _ { 12 } = R \otimes _ { k } 1$, $R _ { 23 } = 1 \otimes _ { k } R$ and $R _ { 13 } = ( 1 \otimes _ { k } \tau _ { V , V } ) ( R \otimes _ { k } 1 ) ( 1 \otimes _ { k } \tau _ { V , V } )$, where $\tau _ { U , V } : U \otimes _ { k } V \rightarrow V \otimes _ { k } U$ is the "twist" mapping defined for $k$-modules $U$ and $V$ by $\tau_{ U , V } ( u \otimes v ) = v \otimes u$ for all $u \in U$ and $v \in V$. Then $R$ satisfies the quantum Yang–Baxter equation in $\square _ { k }\operatorname {Mod}$ if
\begin{equation} \tag{a1} R _ { 12 } R _ { 13 } R _ { 23 } = R _ { 23 } R _ { 13 } R _ { 12 }. \end{equation}
Note that $R$ satisfies (a1) if and only if $B = \tau _ { V , V } R$ satisfies the braid equation in $\square _ { k }\operatorname {Mod}$, which is
\begin{equation} \tag{a2} B _ { 12 } B _ { 23 } B _ { 12 } = B _ { 23 } B _ { 12 } B _ { 23 }. \end{equation}
If $R$ is invertible and satisfies (a2), that is, $R _ { 12 } R _ { 23 } R _ { 12 } = R _ { 23 } R _ { 12 } R _ { 23 }$, then $R$ is a Yang–Baxter operator in $\square _ { k }\operatorname {Mod}$ (see [a5]). There are other formulations of the notion of Yang–Baxter operator in the context of modules; see, e.g., [a8] and [a9].
Observe that the quantum Yang–Baxter and braid equations have natural formulations in any category $\mathcal{C}$ with a suitable notion of tensor product and in which the tensor product of morphisms is defined [a16], [a20], [a34]. The notion of quantum Yang–Baxter operator thus has a natural generalization to categories $\mathcal{C}$ with such additional structure; see, e.g., [a16], [a5].
A good source of solutions to (a1) in $\square _ { k }\operatorname {Mod}$ are certain elements $R = \sum _ { s = 1 } ^ { n } a _ { s } \otimes b _ { s } \in A \otimes _ { k } A$, where $A$ is an algebra over $k$. For $R \in A \otimes _ { k } A$ and a $k$-module $V$, let $R _ { V } : V \otimes _ { k } V \rightarrow V \otimes _ { k } V$ be defined by $R _ { V } ( u \otimes v ) = R \cdot ( u \otimes v )$ for all $u , v \in V$, where $V \otimes _ { k } V$ is regarded as a left $A \otimes _ { k } A$-module under component multiplication. Then $R _ { V }$ is a solution to (a1) for all left $k$-modules $V$ if and only if
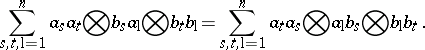 | (a3) |
When $A = M _ { n } ( k )$ is the algebra of $( n \times n )$-matrices over $k$, then an $R \in A \otimes _ { k } A$ which satisfies (a1), or equivalently (a3), is called an $R$-matrix. Suppose that $A = M _ { n } ( k )$ and 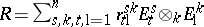 , where $r _ { t \text{l}} ^ { s k } \in k $ and $\{ E _ { t } ^ { s } \} _ { 1 \leq s , t \leq n}$ is the standard basis for $A$. Then (a3) is equivalent to
, where $r _ { t \text{l}} ^ { s k } \in k $ and $\{ E _ { t } ^ { s } \} _ { 1 \leq s , t \leq n}$ is the standard basis for $A$. Then (a3) is equivalent to
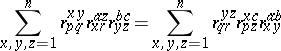 | (a4) |
for all $1 \leq p , q , r , a , b , c \leq n$, which is probably the most familiar form of the quantum Yang–Baxter equation. Ordinarily, (a4) is written using the Einstein summation convention, that is, summation signs are omitted with the understanding that indices that appear as upper and lower indices are summed over their full range of values.
Certain $k$-algebras $A$ with an $R \in A \otimes _ { k } A$ which satisfies (a1) can be used to construct invariants. Quasi-triangular Hopf algebras, in particular quantum algebras (cf. also Quasi-triangular Hopf algebra), give rise to regular isotopy invariants of $1$-$1$ tangles. Ribbon Hopf algebras give rise to regular isotopy invariants of knots and links, and under mild restrictions they give rise to invariants of three-dimensional manifolds. Let $k$ be a field. In this case a finite-dimensional Hopf algebra $A$ over $k$ is closely linked to these structures. The Hopf algebra $A$ is a subHopf algebra of the quantum double $D ( A )$ of $A$, which is a quasi-triangular Hopf algebra [a1]. Every finite-dimensional quasi-triangular Hopf algebra over $k$ is a subHopf algebra of a ribbon Hopf algebra; in particular, $A$ is a subHopf algebra of a ribbon Hopf algebra [a6].
The classification of $R$-matrices seems to be a very daunting task, and most work to date (1998) has involved symbolic computation. Suppose that $k$ is the field of complex numbers. Then the $R$-matrices are completely classified in the $n = 2$ case [a13] and the classification of one basic family is known in the $n = 3$ case [a14].
Some of the more important examples of $R$-matrices, those related to the quantized enveloping algebras, are formal infinite sums or belong to a completed tensor product. See [a4], [a1] for discussion of this important part of the theory.
There is a category $\square _ { A } ^ { A } \mathcal{C}$ with a pre-braiding structure, defined and studied in [a34], associated to a bi-algebra $A$ over $k$ which gives rise to Yang–Baxter operators. Here, the formal variant $\square _ { A } \mathcal{C} ^ { A }$ is considered, whose objects are left $A$-modules and right $A$-comodules $V$ which satisfy the condition
 |
for all $a \in A$ and $v \in V$, where $\rho ( v ) = v ^ { ( 1 ) } \otimes v ^ { ( 2 ) } \in V \otimes _ { k } A$ denotes the coproduct $\rho$ applied to $v \in V$. For an object $V$ of $\square _ { A } \mathcal{C} ^ { A }$, define $\mathcal{R} _ { V } : V \otimes _ { k } V \rightarrow V \otimes _ { k } V$ by $\mathcal{R} _ { V } ( u \otimes v ) = u ^ { \{ 1 \} } \otimes u ^ { ( 2 ) } . v$ for all $u , v \in V$. Then $\mathcal{R} _ { V }$ satisfies (a1). The pre-braiding structure on $\square _ { A } \mathcal{C} ^ { A }$ is the collection of morphisms of the form $\sigma _ { U , V } : U \otimes _ { k } V \rightarrow V \otimes _ { k } U$ which are defined for all pairs of objects $U$, $V$ by $\sigma_{ U , V} ( u \otimes v ) = u ^ { ( 2 ) } . v \otimes u ^ { ( 1 ) }$ for all $u \in U$ and $v \in V$. Observe that $\sigma_{ V , V } = \tau_{ V , V} R _ { V }$ is a solution to the braid equation (a2). When $A$ is a Hopf algebra, the morphism $\sigma_{ U, V}$ is invertible, and the collection of all $\sigma_{ U, V}$ is referred to as a braiding structure. When $k$ is a field and $A$ is a finite-dimensional Hopf algebra over $k$, the category $\square _ { D(A) } \mathcal{C}^{D ( A )}$ can be identified with $\square _{D(A)} \operatorname{Mod}$, the category of left modules of the quantum double [a23].
The FRT construction of [a11], [a10] has an interesting interpretation in light of the preceding paragraph. Suppose that $k$ is a field and $R : V \otimes _ { k } V \rightarrow V \otimes _ { k } V$ is a solution to (a1), where $V$ is a finite-dimensional vector space over $k$. The FRT construction $A ( R )$ is a certain bi-algebra over $k$ associated with $R$. There is a natural way of turning $V$ into an object of $\square _ { A ( R ) } {\cal C} ^ { A ( R) }$ such that $R = \mathcal{R} _ { \mathcal{V} }$, described in [a24]. For a universal description of the FRT construction associated with certain Yang–Baxter operators, see [a5], [a21]. See also [a8] for a discussion of algebras associated with Yang–Baxter operators.
There is a certain quotient $\widetilde { A ( R )}$ of $A ( R )$ which is more closely tied to $R$ from a computational point of view. If $V \neq ( 0 )$, then it is never the case that $A ( R )$ is a Hopf algebra, whereas $\widetilde { A ( R )}$ may very well be a Hopf algebra [a25]. Determining new families of solutions to (a1) of the type described in the preceding paragraph may very well involve using a combination of bi-algebra techniques involving $\widetilde { A ( R )}$ and computer methods [a3], [a25].
There are parametrized versions of (a1), and hence parametrized versions of Yang–Baxter operators. Let $X$ be a set, $R : X \rightarrow \operatorname { End } _ { k } ( V \otimes _ { k } V )$ be a function and suppose that $Z \subseteq X \times X$ is a non-empty subset with a (multiplication) mapping $Z \rightarrow X$. Then $R$ satisfies the $1$-parameter quantum Yang–Baxter equation if
\begin{equation*} R ( x ) _ { 12 } R ( x y ) _ { 13 } R ( y ) _ { 23 } = R ( y ) _ { 23 } R ( x y ) _ { 13 } R ( x ) _ { 12 } \end{equation*}
holds for all $( x , y ) \in Z$. There is an FRT construction for $1$-parameter families [a3]. A $2$-parameter family of solutions to the quantum Yang–Baxter equation is a function $R : X \times X \rightarrow \operatorname { End } _ { k } ( V \otimes _ { k } V )$ which satisfies
\begin{equation*} R ( x , y ) _ { 12 } R ( x , z ) _ { 13 } R ( y , z ) _ { 23 } = \end{equation*}
\begin{equation*} = R ( y , z ) _ { 23 } R ( x , z ) _ { 13 } R ( x , y ) _ { 12 } \end{equation*}
for all $x , y , z \in X$. For examples and discussion, see [a1], [a12], [a11], [a15], [a19].
References
| [a1] | V.G. Drinfel'd, "Quantum groups" , Proc. Internat. Congress Mathematicians Berkeley, California, (1987) , Amer. Math. Soc. (1988) pp. 798–820 |
| [a2] | C. Kassel, "Quantum groups" , Graduate Texts Math. , 155 , Springer (1995) |
| [a3] | L.A. Lambe, D.E. Radford, "Introduction to the quantum Yang–Baxter equation and quantum groups: An algebraic approach" , Kluwer Acad. Publ. (1997) |
| [a4] | V. Chari, A. Pressley, "A guide to quantum groups" , Cambridge Univ. Press (1994) (Corrected reprint: 1995) |
| [a5] | P. Schauenburg, "On coquasitriangular Hopf algebras and the quantum Yang–Baxter equation" , Algebra Berichte , 67 , R. Fischer (1992) |
| [a6] | N.Yu. Reshetikhin, V.G. Turaev, "Ribbon graphs and their invariants derived from quantum groups" Comm. Math. Phys. , 127 (1990) pp. 1–26 |
| [a7] | R. Baxter, "Exactly solved models in stastistical mechanics" , Acad. Press (1982) |
| [a8] | Yu.I. Manin, "Quantum groups and noncommutative geometry" Centre de Recherche Math. Univ. Montreal (1988) |
| [a9] | V.G. Turaev, "The Yang–Baxter equation and invariants of links" Invent. Math. , 92 : 3 (1988) pp. 527–553 |
| [a10] | L.D. Faddeev, N.Yu. Reshetikhin, L.A. Takhtadzhan, "Quantization of Lie groups and Lie algebras" Leningrad Math. J. , 1 (1990) pp. 193–225 Algebra Anal. , 1 (1989) pp. 178–206 |
| [a11] | L.D. Faddeev, N.Yu. Reshetikhin, L.A. Takhtadzhan, "Quantum groups" , Braid group, knot theory and statistical mechanics , Adv. Ser. Math. Phys. , 9 , World Sci. (1989) pp. 97–110 |
| [a12] | L.D. Faddeev, N.Yu. Reshetikhin, L.A. Takhtadzhan, "Quantization of Lie groups and Lie algebras" , Algebraic analysis, Papers Dedicated to Prof. Mikio Sato on the Occasion of his Sixtieth Birthday , I , Acad. Press (1988) pp. 129–139 |
| [a13] | J. Hietarinta, "Solving the two-dimensional constant quantum Yang-Baxter equation" J. Math. Phys. , 34 (1993) pp. 1725–1756 |
| [a14] | J. Hietarinta, "The upper triangular solutions to the three-state constant quantum Yang-Baxter equation" J. Phys. A , 26 (1993) pp. 7077–7095 |
| [a15] | M. Jimbo, "A $q$-difference analogue of $U ( g )$ and the Yang–Baxter equation" Lett. Math. Phys. , 10 (1985) pp. 63–69 |
| [a16] | A. Joyal, R. Street, "Braided tensor categories" Adv. Math. , 102 (1993) pp. 20–78 |
| [a17] | L.H. Kauffman, "Knots and physics" , Ser. Knots and Everything , 1 , World Sci. (1991) |
| [a18] | L.H. Kauffman, S. Lins, "Temperley–Lieb recoupling theory and invariants of $3$-manifolds" , Ann. Math. Studies , 134 , Princeton Univ. Press (1994) |
| [a19] | P.P. Kulish, N.Yu. Reshetikhin, E.K. Sklyanin, "Yang–Baxter equation and representation theory: I" Lett. Math. Phys. , 5 (1981) pp. 393–403 |
| [a20] | L.A. Lambe, D.E. Radford, "Algebraic aspects of the quantum Yang-Baxter equation" J. Algebra , 154 (1993) pp. 228–288 |
| [a21] | R.G. Larson, J. Towber, "Two dual classes of bialgebras related to the concepts of `quantum groups' and `quantum lie algebras'" Commun. Algebra , 19 (1991) pp. 3295–3345 |
| [a22] | S. Majid, "Foundations of quantum group theory" , Cambridge Univ. Press (1995) |
| [a23] | S. Majid, "Doubles of quasi triangular Hopf algebras" Commun. Algebra , 19 (1991) pp. 3061–3073 |
| [a24] | D.E. Radford, "Solutions to the quantum Yang–Baxter equation and the Drinfel'd double" J. Algebra , 161 (1993) pp. 20–32 |
| [a25] | D.E. Radford, "Solutions to the quantum Yang–Baxter equation arising from pointed bi-algebras" Trans. Amer. Math. Soc. , 343 (1994) pp. 455–477 |
| [a26] | N. Reshetikhin, "Invariants of links and $3$-manifolds related to quantum groups" , Proc. Internat. Congr. Math., Kyoto, August, 21-29, 1990 , II , Springer (1991) pp. 1373–1375 |
| [a27] | N.Yu. Reshetikhin, V.G. Turaev, "Invariants of $3$-manifolds via link polynomials and quantum groups" Invent. Math. , 103 (1991) pp. 547–597 |
| [a28] | G.M. D'Ariano, A. Montorsi, M.G. Rasetti, "Integrable systems in statistical mechanics" , Ser. Adv. Statist. Mech. , 1 , World Sci. (1985) |
| [a29] | S. Shnider, S. Sternberg, "Quantum groups. From coalgebras to Drinfel'd algebras. A guided tour" , Graduate Texts Math. Phys. , II , Internat. Press (1993) |
| [a30] | Y. Akutsu, T. Deguchi, M. Wadati, "Exactly solvable models and knot theory" Physics Reports. A Review Section of Physics Lett. , 180 (1989) pp. 247–332 |
| [a31] | C.N. Yang, "Some exact results for the many-body problem in one dimension with repulsive delta-function interaction" Phys. Rev. Lett. , 19 (1967) pp. 1312–1315 |
| [a32] | C.N. Yang, M.L. Ge, "Braid group, knot theory and statistical mechanics" , Adv. Ser. Math. Phys. , 9 , World Sci. (1989) |
| [a33] | C.N. Yang, M.L. Ge, "Braid group, knot theory and statistical mechanics, II" , Adv. Ser. Math. Phys. , 17 , World Sci. (1994) |
| [a34] | D.N. Yetter, "Quantum groups and representations of monoidal categories" Math. Proc. Cambridge Philos. Soc. , 108 (1990) pp. 261–290 |
| [a35] | A.B. Zamolodchikov, A.B. Zamolodchikov, "Factorized $S$-matrices in two dimensions as the exact solutions of certain relativistic quantum field theory models" Ann. Phys. , 120 (1975) pp. 253–291 |
Yang-Baxter operators. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Yang-Baxter_operators&oldid=37607