|
|
| Line 1: |
Line 1: |
| − | {{TEX|part}} | + | <!--This article has been texified automatically. Since there was no Nroff source code for this article, |
| | + | the semi-automatic procedure described at https://encyclopediaofmath.org/wiki/User:Maximilian_Janisch/latexlist |
| | + | was used. |
| | + | If the TeX and formula formatting is correct, please remove this message and the {{TEX|semi-auto}} category. |
| | | | |
| − | ====Duality in algebraic geometry====
| + | Out of 94 formulas, 91 were replaced by TEX code.--> |
| | | | |
| − | Duality between the different cohomology spaces on [[Algebraic variety|algebraic varieties]].
| + | {{TEX|semi-auto}}{{TEX|partial}} |
| | + | Let $M$ be a [[Matroid|matroid]] with rank function $r$ on the ground set $E$. The Tutte polynomial $t ( M ; x , y )$ of $M$ is defined by |
| | | | |
| − | [[Cohomology]] of [[Coherent sheaf|coherent sheaves]]. Let $X$ be a non-singular [[algebraic variety]] of dimension $n$ over an algebraically closed field $k$ and let $\mathcal{L}$ be a locally free sheaf on $X$. Serre's duality theorem states that the finite-dimensional cohomology (vector) spaces $H^i(X,\mathcal{L})$ and $H^{n-i}(X,\check{\mathcal{L}}\otimes\omega_X)$ are mutually dual. Here $\omega_X=\Omega_X^n$ is the [[sheaf]] of germs of regular differential forms of degree $n$ on $X$, and $\check{\mathcal{L}}=\operatorname{Hom}(\mathcal{L},\mathcal{O}_X)$ is the [[locally free sheaf]] dual to $\mathcal{L}$. If $\mathcal{L}=\mathcal{O}_X(D)$ is the [[invertible sheaf]] corresponding to a [[divisor]] $D$ on $X$, this theorem establishes the equality
| + | \begin{equation*} t ( M ; x , y ) = \sum _ { S \subseteq E } ( x - 1 ) ^ { r ( M ) - r ( S ) } ( y - 1 ) ^ { | S | - r ( S )}. \end{equation*} |
| | | | |
| − | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d034/d034120/d03412016.png" /></td> </tr></table>
| + | One also writes $t ( M )$ for $t ( M ; x , y )$ when no confusion can arise about the values of $x$ and $y$. There are several equivalent reformulations of $t ( M )$; the most useful such expression is recursive, using the matroid operations of deletion and contraction: |
| | | | |
| − | where <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d034/d034120/d03412017.png" /> is the [[canonical divisor]] on <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d034/d034120/d03412018.png" />. If <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d034/d034120/d03412019.png" />, a relation equivalent to the above was found as early as the 19th century. There exists a generalization of Serre's theorem to the case of cohomology of arbitrary coherent sheaves on complete algebraic varieties [[#References|[1]]], [[#References|[4]]]. In particular, if the variety <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d034/d034120/d03412020.png" /> is a Cohen–Macaulay subvariety (e.g. a locally complete intersection) of codimension <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d034/d034120/d03412021.png" /> in a non-singular projective variety <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d034/d034120/d03412022.png" />, there is duality between the <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d034/d034120/d03412023.png" />-space <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d034/d034120/d03412024.png" /> and the space of global Ext's
| + | T0) If $E = \emptyset$, then $t ( M ) = 1$; |
| | | | |
| − | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d034/d034120/d03412025.png" /></td> </tr></table>
| + | T1) If $e$ is an isthmus, then $t ( M ) = x t ( M / e )$; |
| | | | |
| − | where <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d034/d034120/d03412026.png" /> is a coherent sheaf on <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d034/d034120/d03412027.png" />, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d034/d034120/d03412028.png" /> (Grothendieck's dualizing sheaf), while <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d034/d034120/d03412029.png" />. Here, the sheaf <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d034/d034120/d03412030.png" /> is invertible if and only if <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d034/d034120/d03412031.png" /> is a Gorenstein scheme (cf. [[Gorenstein ring|Gorenstein ring]]).
| + | T2) If $e$ is a loop, then $t ( M ) = y t ( M - e )$; |
| | | | |
| − | Etale cohomology. Let <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d034/d034120/d03412032.png" /> be a complete connected non-singular algebraic variety of dimension <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d034/d034120/d03412033.png" /> over an algebraically closed field <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d034/d034120/d03412034.png" />; let <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d034/d034120/d03412035.png" /> be an integer which is relatively prime to the characteristic of the field <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d034/d034120/d03412036.png" />; let <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d034/d034120/d03412037.png" /> be a locally free (in the étale topology) sheaf of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d034/d034120/d03412038.png" />-modules on <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d034/d034120/d03412039.png" />; and let <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d034/d034120/d03412040.png" /> be the sheaf of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d034/d034120/d03412041.png" />-th power roots of unity. Then there exists a non-degenerate pairing of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d034/d034120/d03412042.png" />-modules [[#References|[6]]]:
| + | T3) If $e$ is neither an isthmus nor a loop, then $t ( M ) = t ( M / e ) + t ( M - e )$. |
| | | | |
| − | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d034/d034120/d03412043.png" /></td> </tr></table>
| + | Some standard evaluations of the Tutte polynomial are: |
| | | | |
| − | A more general duality theorem concerns smooth, but not necessarily complete, varieties [[#References|[5]]]. There exists a non-degenerate pairing of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d034/d034120/d03412044.png" />-modules
| + | a) $t ( M ; 1,1 )$ is the number of bases of $M$; |
| | | | |
| − | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d034/d034120/d03412045.png" /></td> </tr></table>
| + | b) $t ( M ; 2,1 )$ is the number of independent subsets of $M$; |
| | | | |
| − | where cohomology with compact support is found on the left-hand side. If the field <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d034/d034120/d03412046.png" /> is the algebraic closure of a field <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d034/d034120/d03412047.png" />, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d034/d034120/d03412048.png" /> and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d034/d034120/d03412049.png" />, then the [[Galois group|Galois group]] <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d034/d034120/d03412050.png" /> acts on <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d034/d034120/d03412051.png" /> and the preceding pairing is a pairing of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d034/d034120/d03412052.png" />-modules.
| + | c) $t ( M ; 1,2 )$ is the number of spanning subsets of $M$; |
| | | | |
| − | Poincaré's duality theorem is an analogue of the first of the theorems given for <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d034/d034120/d03412053.png" />-adic cohomology: There exists a non-degenerate pairing of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d034/d034120/d03412054.png" />-modules
| + | d) $t ( M ; 2,2 ) = 2 ^ { | E | }$. |
| | | | |
| − | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d034/d034120/d03412055.png" /></td> </tr></table>
| + | When a matroid $M$ is constructed from other matroids $M _ { 1 } , M _ { 2 } , \ldots$, it is frequently possible to compute $t ( M )$ from the $t ( M _ { i } )$. The most fundamental structural result of this kind concerns the direct sum of matroids: $t ( M _ { 1 } \oplus M _ { 2 } ) = t ( M _ { 1 } ) t ( M _ { 2 } )$. Another fundamental structural property of the Tutte polynomial is its transparent relationship with matroid duality: $t ( M ^ { * } ; x , y ) = t ( M ; y , x )$. Many related results can be found in [[#References|[a3]]]. |
| | | | |
| − | where <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d034/d034120/d03412056.png" /> is the Tate sheaf, which is non-canonically isomorphic to the sheaf <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d034/d034120/d03412057.png" /> (cf. [[L-adic-cohomology|<img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d034/d034120/d03412058.png" />-adic cohomology]]). Hence the isomorphism of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d034/d034120/d03412059.png" />-spaces
| + | The Tutte polynomial has many significant connections with invariants in [[Graph theory|graph theory]]. Of central importance is the relationship between $t ( M )$ and the chromatic polynomial $\chi ( G ; \lambda )$ of a graph $G$ (cf. also [[Graph colouring|Graph colouring]]). If $G$ is a graph having $v ( G )$ vertices and $c ( G )$ connected components, then |
| | | | |
| − | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d034/d034120/d03412060.png" /></td> </tr></table>
| + | \begin{equation*} \chi ( G ; \lambda ) = \lambda ^ { c ( G ) } ( - 1 ) ^ { v ( G ) - c ( G ) } t ( M _ { G } , 1 - \lambda , 0 ), \end{equation*} |
| | | | |
| − | and, in particular, the equality of the Betti numbers
| + | where $M _ { G }$ is the cycle matroid of $G$ (cf. also [[Matroid|Matroid]]). Thus, when $G$ is planar (cf. [[Graph, planar|Graph, planar]]), $t ( M _ { G } ; x , y )$ simultaneously carries information concerning proper colourings of $G$ along with proper colourings of its [[dual graph]] $G ^ { * }$. This is the reason W.T. Tutte referred to it as a dichromatic polynomial in his foundational work in this area [[#References|[a14]]]. The polynomial was generalized from graphs to matroids by H.H. Crapo [[#References|[a5]]] and T.H. Brylawski [[#References|[a2]]]. |
| | | | |
| − | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d034/d034120/d03412061.png" /></td> </tr></table>
| + | Other invariants which can be obtained from the Tutte polynomial include the beta invariant $\beta ( M )$, the Möbius function $\mu ( M )$, and the characteristic polynomial $p ( M ; \lambda )$ of a matroid $M$. See [[#References|[a16]]] for more information about these invariants. |
| | | | |
| − | As in the case of cohomology of coherent sheaves, these results can be generalized to the relative case of a proper scheme morphism, formulated in the language of derived categories [[#References|[6]]].
| + | ==Applications== |
| | + | The Tutte polynomial has applications in various areas, some of which are given below. For an extensive introduction, see [[#References|[a4]]]. |
| | | | |
| − | Other cohomology theories. Analogues of Poincaré's theorem are valid in the theory of crystalline cohomology [[#References|[7]]], and de Rham cohomology over a field of characteristic zero [[#References|[8]]]. In number-theoretic applications cohomology of sheaves on the flat Grothendieck topology of arithmetic schemes are important. Duality theorems [[#References|[9]]] are applicable to special cases of such cohomology theories.
| + | [[Acyclic orientation]]s: Let $a ( G )$ denote the number of acyclic orientations of a graph $G$. Then R. Stanley [[#References|[a13]]] proved that $a ( G ) = t ( M _ { G } ; 2,0 )$. A variety of related evaluations appear in [[#References|[a9]]]. |
| | | | |
| | + | The critical problem of Crapo and G.-C. Rota [[#References|[a7]]]: Let $M$ be a rank-$r$ matroid which is represented over $\operatorname {GF} ( q )$ by $\phi : E \rightarrow \operatorname {GF} ( q ) ^ { n }$ and let $k$ be a positive integer. Then the number of $k$-tuples of linear functionals on $\operatorname{GF} ( q ) ^ { n }$ which distinguish $\phi ( E )$ equals $( - 1 ) ^ { r } q ^ { k ( n - r ) } t ( M ; 1 - q ^ { k } , 0 )$. See [[#References|[a12]]] for extensions of the critical problem. |
| | | | |
| | + | Coding theory: Let $C$ be a linear [[Code|code]] over $\operatorname {GF} ( q )$ with code-weight polynomial $A ( C ; q , z ) = \sum _ { \mathbf{v} \in C } z ^ { w (\mathbf{v}) }$, where $w ( \mathbf{v} )$ is the weight of the code word $\mathbf{v}$ (see also [[Coding and decoding|Coding and decoding]]). Then |
| | | | |
| − | =====References===== | + | \begin{equation*} A ( C , q , z ) = ( 1 - z ) ^ { r } z ^ { n - r } t \left( M _ { C } ; \frac { 1 + ( q - 1 ) z } { 1 - z } , \frac { 1 } { z } \right), \end{equation*} |
| | | | |
| − | <table>
| + | where $M _ { C }$ is the matroid associated with the code $C$. Many standard results in coding theory have interpretations using the Tutte polynomial [[#References|[a4]]]. |
| − | <TR><TD valign="top">[1]</TD> <TD valign="top"> A. Grothendieck, "The cohomology theory of abstract algebraic varieties" , ''Proc. Internat. Math. Congress Edinburgh, 1958'' , Cambridge Univ. Press (1960) pp. 103–118 {{MR|0130879}} {{ZBL|0119.36902}} </TD></TR>
| |
| − | <TR><TD valign="top">[2]</TD> <TD valign="top"> I.V. Dolgachev, "Abstract algebraic geometry" ''J. Soviet Math.'' , '''2''' : 3 (1974) pp. 264–303 ''Itogi Nauk. i Tekhn. Algebra. Topol. Geom.'' , '''10''' (1972) pp. 47–112 {{MR|}} {{ZBL|1068.14059}} </TD></TR>
| |
| − | <TR><TD valign="top">[3]</TD> <TD valign="top"> J.-P. Serre, "Faisceaux algébriques cohérents" ''Ann. of Math.'' , '''61''' (1955) pp. 197–258 {{MR|0068874}} {{ZBL|0067.16201}} </TD></TR>
| |
| − | <TR><TD valign="top">[4]</TD> <TD valign="top"> R. Hartshorne, "Residues and duality" , Springer (1966) {{MR|0222093}} {{ZBL|0212.26101}} </TD></TR>
| |
| − | <TR><TD valign="top">[5]</TD> <TD valign="top"> "Théorie des topos et cohomologie étale des schémas" M. Artin (ed.) A. Grothendieck (ed.) J.-L. Verdier (ed.) , ''Sem. Geom. Alg.'' , '''3''' , Springer (1973) {{MR|0354654}} {{ZBL|}} </TD></TR>
| |
| − | <TR><TD valign="top">[6]</TD> <TD valign="top"> J.-L. Verdier, "A duality theorem in the etale cohomology of schemes" T.A. Springer (ed.) et al. (ed.) , ''Proc. Conf. local fields (Driebergen, 1966)'' , Springer (1967) pp. 184–198 {{MR|0230732}} {{ZBL|0184.24402}} </TD></TR>
| |
| − | <TR><TD valign="top">[7]</TD> <TD valign="top"> P. Berthelot, "Cohomologie cristalline des schémas de caractéristique <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d034/d034120/d03412062.png" />" , Springer (1974) {{MR|0384804}} {{ZBL|0298.14012}} </TD></TR>
| |
| − | <TR><TD valign="top">[8]</TD> <TD valign="top"> R. Hartshorne, "Ample subvarieties of algebraic varieties" , Springer (1970) {{MR|0282977}} {{ZBL|0208.48901}} </TD></TR>
| |
| − | <TR><TD valign="top">[9]</TD> <TD valign="top"> B. Mazur, "Local flat duality" ''Amer. J. Math.'' , '''92''' (1970) pp. 343–361 {{MR|0271119}} {{ZBL|0199.24501}} </TD></TR>
| |
| − | <TR><TD valign="top">[10]</TD> <TD valign="top"> A. Altman, S. Kleiman, "Introduction to Grothendieck duality theory" , Springer (1970) {{MR|0274461}} {{ZBL|0215.37201}} </TD></TR>
| |
| − | <TR><TD valign="top">[11]</TD> <TD valign="top"> J. Milne, "Arithmetic duality theorems" , Acad. Press (1987) {{MR|2261462}} {{MR|0881804}} {{ZBL|1127.14001}} {{ZBL|0613.14019}} </TD></TR>
| |
| − | </table>
| |
| − | | |
| − | | |
| − | | |
| − | ====Duality in algebraic topology (by G.S. Chogoshvili)====
| |
| − | | |
| − | A situation in which the values of certain topological invariants determine the values of others. In algebraic topology duality manifest itself: in duality (in the sense of the theory of characters) between the homology and cohomology groups of the same dimension with dual groups of coefficients; in the isomorphism between homology and cohomology groups of complementary dimensions of a variety ([[Poincaré duality|Poincaré duality]]); in the isomorphism between the homology and cohomology groups of mutually complementary sets of a space ([[Alexander duality|Alexander duality]]); in the mutual exchangeability, in certain situations, of homotopy and cohomotopy, as well as of homology and cohomology, groups which, in the absence of additional restrictions imposed on the dimension of the space, is valid not for ordinary, but rather for <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d034/d034120/d03412063.png" />-homotopy and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d034/d034120/d03412064.png" />-cohomotopy groups (see [[S-duality|<img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d034/d034120/d03412065.png" />-duality]]).
| |
| − | | |
| − | The duality between homology and cohomology consists in the following. Let <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d034/d034120/d03412066.png" /> be an arbitrary [[Homology theory|homology theory]] over some admissible category of pairs of spaces and their mappings, i.e. a system which satisfies the [[Steenrod–Eilenberg axioms|Steenrod–Eilenberg axioms]] of homology theory with discrete or compact Abelian groups <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d034/d034120/d03412067.png" />. Then the system <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d034/d034120/d03412068.png" /> (where <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d034/d034120/d03412069.png" /> is the group of characters of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d034/d034120/d03412070.png" />, and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d034/d034120/d03412071.png" /> and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d034/d034120/d03412072.png" /> are the homomorphisms, conjugate, respectively, with <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d034/d034120/d03412073.png" /> and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d034/d034120/d03412074.png" />) satisfies the Steenrod–Eilenberg axioms of cohomology theory and represents the cohomology theory over the same category with compact or, respectively, discrete groups <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d034/d034120/d03412075.png" />. A dual homology theory can be constructed for any cohomology theory in such a manner. Consequently, homology and cohomology theories are dual pairs; the transformation of one theory into the other, up to natural equivalences, is an involution. For any theorem of homology theory, i.e. a theorem about the system <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d034/d034120/d03412076.png" />, there exists a dual proposition about the system <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d034/d034120/d03412077.png" />, i.e. a theorem of cohomology theory, and vice versa. On passing to a dual proposition, groups are replaced by groups of characters, homomorphisms change direction, subgroups are replaced by quotient groups, and vice versa. The Steenrod–Eilenberg axioms themselves may serve as examples. For specific categories or theories the construction of this duality is realized, for example, in the following manner. Let <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d034/d034120/d03412078.png" /> be a (finite) [[Complex|complex]]. The number
| |
| − | | |
| − | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d034/d034120/d03412079.png" /></td> </tr></table>
| |
| − | | |
| − | is taken to be the product of the <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d034/d034120/d03412080.png" />-dimensional chain <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d034/d034120/d03412081.png" /> of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d034/d034120/d03412082.png" /> over a discrete or compact coefficient group <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d034/d034120/d03412083.png" /> and the <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d034/d034120/d03412084.png" />-dimensional cochain <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d034/d034120/d03412085.png" /> of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d034/d034120/d03412086.png" /> over the coefficient group <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d034/d034120/d03412087.png" /> dual with <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d034/d034120/d03412088.png" /> in the sense of the theory of characters. This product defines the multiplication of a homology class by a cohomology class, and converts <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d034/d034120/d03412089.png" />-dimensional homology and cohomology into mutual groups of characters. Two types of homology groups — projective and spectral — exist for infinite complexes. Spectral homology groups are the limits of the direct spectra of the homology groups of closed finite subcomplexes, ordered by inclusion, while the projective homology groups are the homology groups of the limits of direct spectra of the chain groups of these finite subcomplexes. Cohomology groups are obtained in a similar manner as the limits of the corresponding inverse spectra. For a discrete group of coefficients both homology groups coincide, and yield a homology group of finite cycles; if the group is compact, the cohomology groups coincide and give a cohomology group of infinite cocycles. The duality existing in finite complexes generates the mutual duality of projective groups and the mutual duality of spectral groups in infinite complexes, and these two last-named dualities (by way of singular complexes, nerves of coverings, etc.) represent the duality between an <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d034/d034120/d03412090.png" />-dimensional projective (spectral) homology group <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d034/d034120/d03412091.png" /> of a space <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d034/d034120/d03412092.png" /> over a discrete or a compact coefficient group <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d034/d034120/d03412093.png" /> in any theory (theories of [[Singular homology|singular homology]] and cohomology; [[Aleksandrov–Čech homology and cohomology|Aleksandrov–Čech homology and cohomology]]; [[Vietoris homology|Vietoris homology]] and cohomology; etc.) and an <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d034/d034120/d03412094.png" />-dimensional projective (spectral) cohomology group <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d034/d034120/d03412095.png" /> in the same theory over the group <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d034/d034120/d03412096.png" /> dual to <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d034/d034120/d03412097.png" /> [[#References|[1]]], [[#References|[3]]], , [[#References|[9]]]:
| |
| − | | |
| − | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d034/d034120/d03412098.png" /></td> </tr></table>
| |
| − | | |
| − | The relations between the invariants which express the connectivities of a manifold in complementary dimensions were established by H. Poincaré in the first study on algebraic topology (1895). He showed that for an <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d034/d034120/d03412099.png" />-dimensional orientable manifold, its <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d034/d034120/d034120100.png" />-dimensional and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d034/d034120/d034120101.png" />-dimensional Betti numbers are equal, as are the <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d034/d034120/d034120102.png" />- and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d034/d034120/d034120103.png" />-dimensional torsion coefficients. This theorem was strengthened by O. Veblen (1923) who formulated it for homology bases, while the use of cohomology groups imparted it a form expressive of the content of this duality. In order to obtain this form, it is necessary to put into correspondence each <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d034/d034120/d034120104.png" />-dimensional chain <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d034/d034120/d034120105.png" />, given on any triangulation <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d034/d034120/d034120106.png" /> of an <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d034/d034120/d034120107.png" />-dimensional oriented [[Homology manifold|homology manifold]] <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d034/d034120/d034120108.png" /> and taking values in a discrete or compact coefficient group <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d034/d034120/d034120109.png" />, with an <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d034/d034120/d034120110.png" />-dimensional cochain of the cellular complex <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d034/d034120/d034120111.png" /> of barycentric stars of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d034/d034120/d034120112.png" />, which assumes, on any star, the value of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d034/d034120/d034120113.png" /> on the simplex corresponding to this star. Since the groups of the complexes <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d034/d034120/d034120114.png" /> and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d034/d034120/d034120115.png" /> are identical, this correspondence defines an isomorphism of the homology and cohomology groups of complementary dimensions of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d034/d034120/d034120116.png" />:
| |
| − | | |
| − | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d034/d034120/d034120117.png" /></td> </tr></table>
| |
| − | | |
| − | Here, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d034/d034120/d034120118.png" /> may also be a module, and if the manifold is not orientable, the theorem is true modulo 2. Replacing the group <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d034/d034120/d034120119.png" /> by its dual group <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d034/d034120/d034120120.png" /> yields the duality [[#References|[1]]]:
| |
| − | | |
| − | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d034/d034120/d034120121.png" /></td> </tr></table>
| |
| − | | |
| − | which is also of interest because its product is the intersection index of cycles, arbitrarily selected from the classes undergoing multiplication [[#References|[1]]], [[#References|[11]]], [[#References|[12]]], [[#References|[13]]], [[#References|[15]]], [[#References|[16]]].
| |
| − | | |
| − | J. Alexander's theorem (1922) completed a major stage (initially a set-theoretic stage) in finding the topological properties of a set that are determined by the topological properties of its complement. The theorem states that the <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d034/d034120/d034120122.png" />-dimensional Betti number modulo 2 of a polyhedron situated in the <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d034/d034120/d034120123.png" />-dimensional sphere is equal to the <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d034/d034120/d034120124.png" />-dimensional Betti number modulo 2 of the complement (cf. [[Alexander duality|Alexander duality]]).
| |
| − | | |
| − | This theorem in turn served as the base for a number of investigations which affected to a considerable extent the development of algebraic topology. These studies were conducted with a view to generalizing classes of spaces (plane Euclidean spaces, spheres and manifolds of arbitrary dimension, locally compact spaces, etc.), their subsets (polyhedra, closed subsets, arbitrary subsets) and domains of coefficients (integers modulo 2, the group of integers, the field of rational numbers, other specific groups and fields, arbitrary Abelian groups, topological (mainly compact) Abelian groups, etc.) to which Alexander duality applies, and also strengthening of the relations connecting mutually complementary sets (equality of Betti numbers, group isomorphism, duality of topological groups, natural and connecting homomorphisms, etc.). Several results thus obtained may be represented in the form of the following diagram [[#References|[1]]], [[#References|[3]]], , [[#References|[5]]], , [[#References|[7]]], , [[#References|[9]]], [[#References|[11]]]:
| |
| − | | |
| − | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d034/d034120/d034120125.png" /></td> </tr></table>
| |
| − | | |
| − | where <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d034/d034120/d034120126.png" /> is a discrete or compact group of coefficients, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d034/d034120/d034120127.png" />, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d034/d034120/d034120128.png" /> and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d034/d034120/d034120129.png" /> are mutually complementary sets of an <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d034/d034120/d034120130.png" />-dimensional spherical manifold <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d034/d034120/d034120131.png" />, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d034/d034120/d034120132.png" /> and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d034/d034120/d034120133.png" /> are the <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d034/d034120/d034120134.png" />-dimensional Aleksandrov–Čech homology and cohomology groups (with compact support) of the set <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d034/d034120/d034120135.png" /> over <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d034/d034120/d034120136.png" /> and, respectively, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d034/d034120/d034120137.png" />, and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d034/d034120/d034120138.png" /> and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d034/d034120/d034120139.png" /> are the <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d034/d034120/d034120140.png" />-dimensional Aleksandrov–Čech spectral homology and cohomology groups of the set <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d034/d034120/d034120141.png" /> over <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d034/d034120/d034120142.png" /> and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d034/d034120/d034120143.png" />, respectively. The indicated relations in the diagram, obtained by different workers and by different methods, are coordinated to the extent that the corresponding elements in the isomorphisms represent the same character of the remaining groups for vertical and horizontal dualities. They are thus various forms of the same duality theorem. The upper duality is a link duality, i.e. its product of elements is the [[Linking coefficient|linking coefficient]] of cycles, arbitrarily selected from the multiplier classes or, in the case of a compact group <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d034/d034120/d034120144.png" />, is defined by continuity of the cycle linkage. In the diagram given above, the groups of the first column may be replaced by the <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d034/d034120/d034120145.png" />-dimensional Steenrod homology and cohomology groups with compact supports, while the groups in the second column can be replaced by the <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d034/d034120/d034120146.png" />-dimensional projective Aleksandrov–Čech homology and cohomology groups. Then, for a compact <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d034/d034120/d034120147.png" />, the isomorphism of the main diagonal yields the Steenrod duality theorem in its original form if the cohomology group of the set <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d034/d034120/d034120148.png" /> is replaced, in accordance with Poincaré's theorem, by the <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d034/d034120/d034120149.png" />-dimensional homology group of infinite cycles. If the group <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d034/d034120/d034120150.png" /> is compact, the diagrams are isomorphic; if, in addition, the set <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d034/d034120/d034120151.png" /> is compact as well, the duality of the top line of the diagram represents the theorem obtained by L.S. Pontryagin [[#References|[1]]] in 1934 (cf. [[Pontryagin duality|Pontryagin duality]]). For other generalizations and trends of study see [[#References|[2]]], [[#References|[10]]], [[#References|[14]]], [[#References|[15]]], [[#References|[16]]]. | |
| − | | |
| − | An important form of Alexander duality, which concerns the connecting homomorphism and the exactness axiom, is the isomorphism between homology groups and between cohomology groups of adjacent dimensions. These isomorphisms, determined by P.S. Aleksandrov and A.N. Kolmogorov, state that the <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d034/d034120/d034120152.png" />-dimensional homology (cohomology) group of a closed set <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d034/d034120/d034120153.png" /> of a normal locally compact space <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d034/d034120/d034120154.png" /> which is acyclic in dimensions <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d034/d034120/d034120155.png" /> and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d034/d034120/d034120156.png" />, over a compact (discrete) group <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d034/d034120/d034120157.png" />, is isomorphic to the <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d034/d034120/d034120158.png" />-dimensional homology (cohomology) group of the complement:
| |
| − | | |
| − | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d034/d034120/d034120159.png" /></td> </tr></table>
| |
| − | | |
| − | and
| |
| − | | |
| − | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d034/d034120/d034120160.png" /></td> </tr></table>
| |
| − | | |
| − | Pontryagin's theorem is deduced from these isomorphisms. Aleksandrov [[#References|[2]]] obtained these isomorphisms from the general duality relations relating homology and cohomology groups of mutually complementary sets and the space, as well as various kernels, images and quotient groups under imbedding and excision homomorphisms. These relations also carry a large amount of other important information about the positioning of sets in space. Aleksandrov [[#References|[2]]] obtained them with the aid of spectral homology and cohomology groups with respect to the so-called singular subcomplexes of nerves consisting of simplices, the closures of the vertices of which are non-compact. Kolmogorov proved the above duality isomorphisms by way of his functional homology and cohomology groups (cf. [[Kolmogorov duality|Kolmogorov duality]]). These and other dualities (e.g. [[Lefschetz duality|Lefschetz duality]]) are connected by various relations. They may also be considered as consequences of some general duality in which the so-called exterior groups of a set, which are direct limits of the cohomology groups of the neighbourhoods of this set ordered by imbedding, participate [[#References|[3]]], , [[#References|[5]]], , [[#References|[7]]], [[#References|[12]]], [[#References|[13]]]. Connections between different dualities assume a novel aspect if viewed from the point of view of [[Sheaf theory|sheaf theory]].
| |
| − | | |
| − | | |
| − | | |
| − | =====References=====
| |
| − | | |
| − | <table>
| |
| − | <TR><TD valign="top">[1]</TD> <TD valign="top"> L.S. Pontryagin, "Topological duality theorems" ''Uspekhi Mat. Nauk'' , '''2''' : 2 (1947) pp. 21–44 (In Russian) {{MR|0025725}} {{ZBL|}} </TD></TR>
| |
| − | <TR><TD valign="top">[2]</TD> <TD valign="top"> P.S. Aleksandrov, "On homological positioning properties of complexes and closed sets" ''Izv. Akad. Nauk SSSR Ser. Mat.'' , '''6''' (1942) pp. 227–282 (In Russian) {{MR|}} {{ZBL|}} </TD></TR>
| |
| − | <TR><TD valign="top">[3]</TD> <TD valign="top"> P.S. Aleksandrov, "Fundamental duality theorems for non-closed sets" ''Mat. Sb.'' , '''21''' : 2 (1947) pp. 161–232 (In Russian) {{MR|}} {{ZBL|}} </TD></TR>
| |
| − | <TR><TD valign="top">[4a]</TD> <TD valign="top"> P.S. Aleksandrov, "Topological duality theorems I" ''Transl. Amer. Math. Soc. (2)'' , '''30''' (1963) pp. 1–102 ''Trudy Mat. Inst. Steklov.'' , '''48''' (1955) pp. 1–108 {{MR|0155320}} {{ZBL|0127.13402}} </TD></TR>
| |
| − | <TR><TD valign="top">[4b]</TD> <TD valign="top"> P.S. Aleksandrov, "Topological duality theorems II" ''Transl. Amer. Math. Soc. (2)'' , '''30''' (1963) pp. 103–233 ''Trudy Mat. Inst. Steklov.'' , '''54''' (1959) pp. 1–136 {{MR|0155321}} {{ZBL|0127.13403}} </TD></TR>
| |
| − | <TR><TD valign="top">[5]</TD> <TD valign="top"> G.S. Chogoshvili, "The duality theorem for retracts" ''Dokl. Akad. Nauk SSSR'' , '''51''' : 2 (1946) pp. 87–90 (In Russian) {{MR|}} {{ZBL|}} </TD></TR>
| |
| − | <TR><TD valign="top">[6a]</TD> <TD valign="top"> G.S. Chogoshvili, "On homology theory for non-closed sets" , ''General topology and its relations to modern analysis and algebra (Proc. Symp. Prague)'' , Acad. Press (1961) pp. 123–132 {{MR|}} {{ZBL|}} </TD></TR>
| |
| − | <TR><TD valign="top">[6b]</TD> <TD valign="top"> G.S. Chogoshvili, "Generalized products and limits and their application in homology theory" ''Uspekhi Mat. Nauk'' , '''21''' : 4 (1966) pp. 23–34 (In Russian) {{MR|}} {{ZBL|}} </TD></TR>
| |
| − | <TR><TD valign="top">[7]</TD> <TD valign="top"> S. Kaplan, "Homology properties of arbitrary subsets of Euclidean spaces" ''Trans. Amer. Math. Soc.'' , '''62''' (1947) pp. 248–271 {{MR|0024128}} {{ZBL|0034.10902}} </TD></TR>
| |
| − | <TR><TD valign="top">[8a]</TD> <TD valign="top"> K.A. Sitnikov, "Combinatorial topology of non-closed sets I" ''Transl. Amer. Math. Soc. (2)'' , '''15''' (1960) pp. 245–295 ''Mat. Sb.'' , '''34''' (1954) pp. 3–54 {{MR|}} {{ZBL|}} </TD></TR>
| |
| − | <TR><TD valign="top">[8b]</TD> <TD valign="top"> K.A. Sitnikov, "Combinatorial topology of non-closed sets II" ''Transl. Amer. Math. Soc. (2)'' , '''15''' (1960) pp. 297–343 ''Mat. Sb.'' , '''37''' (1955) pp. 385–434 {{MR|}} {{ZBL|}} </TD></TR>
| |
| − | <TR><TD valign="top">[8c]</TD> <TD valign="top"> K.A. Sitnikov, "Combinatorial topology of non-closed sets III" ''Mat. Sb.'' , '''48''' (1959) pp. 213–226 (In Russian) {{MR|}} {{ZBL|}} </TD></TR>
| |
| − | <TR><TD valign="top">[9]</TD> <TD valign="top"> N.A. Berikashvili, "On the axiomatic theory of spectra and duality laws for arbitrary sets" ''Trudy Tbil. Mat. Inst.'' , '''24''' (1957) pp. 409–484 (In Russian) {{MR|}} {{ZBL|}} </TD></TR>
| |
| − | <TR><TD valign="top">[10]</TD> <TD valign="top"> D.S. Baladze, "Steenrod's generalized homology theory" ''Trudy Tbil. Mat. Inst.'' , '''41''' (1972) pp. 41–83 (In Russian) {{MR|}} {{ZBL|}} </TD></TR>
| |
| − | <TR><TD valign="top">[11]</TD> <TD valign="top"> D.G. Bourgin, "Modern algebraic topology" , Macmillan (1963) {{MR|0160201}} {{ZBL|}} </TD></TR>
| |
| − | <TR><TD valign="top">[12]</TD> <TD valign="top"> E.H. Spanier, "Algebraic topology" , McGraw-Hill (1966) {{MR|0210112}} {{MR|1325242}} {{ZBL|0145.43303}} </TD></TR>
| |
| − | <TR><TD valign="top">[13]</TD> <TD valign="top"> R.M. Switzer, "Algebraic topology - homotopy and homology" , Springer (1975) {{MR|0385836}} {{ZBL|0305.55001}} </TD></TR>
| |
| − | <TR><TD valign="top">[14]</TD> <TD valign="top"> E.G. Sklyarenko, "On the theory of generalized manifolds" ''Math. USSR Izv.'' , '''5''' : 4–6 (1971) pp. 845–858 ''Izv. Akad. Nauk SSSR. Ser. Mat.'' , '''35''' : 4 (1971) pp. 831–843 {{MR|}} {{ZBL|}} </TD></TR>
| |
| − | <TR><TD valign="top">[15]</TD> <TD valign="top"> A. Borel, J.C. Moore, "Homology theory for locally compact spaces" ''Mich. Math. J.'' , '''7''' (1960) pp. 137–160 {{MR|0131271}} {{ZBL|0116.40301}} </TD></TR>
| |
| − | <TR><TD valign="top">[16]</TD> <TD valign="top"> G.E. Bredon, "Sheaf theory" , McGraw-Hill (1967) {{MR|0221500}} {{ZBL|0158.20505}} </TD></TR>
| |
| − | </table>
| |
| − | | |
| − | | |
| − | | |
| − | ====Duality in the theory of analytic spaces (by V.P. Palamodov)====
| |
| − | | |
| − | Duality between the various topological vector cohomology spaces of complex spaces. There are three types of duality theorems, which correspond to Poincaré, Lefschetz and Aleksandrov–Pontryagin dualities in topology, but which concern the cohomology spaces <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d034/d034120/d034120161.png" /> of a [[Complex space|complex space]] <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d034/d034120/d034120162.png" /> with values in a [[Coherent analytic sheaf|coherent analytic sheaf]] <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d034/d034120/d034120163.png" /> and supports in the family <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d034/d034120/d034120164.png" /> or in a quotient space of it (see [[Cohomology|Cohomology]] with values in a sheaf).
| |
| − | | |
| − | Serre's duality theorem [[#References|[1]]] belongs to the first type. Let <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d034/d034120/d034120165.png" /> be a complex manifold of dimension <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d034/d034120/d034120166.png" /> with a countable base, let <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d034/d034120/d034120167.png" /> be the sheaf of holomorphic differential forms of degree <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d034/d034120/d034120168.png" /> and let <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d034/d034120/d034120169.png" /> be a locally free [[Analytic sheaf|analytic sheaf]] on <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d034/d034120/d034120170.png" />. For each integer <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d034/d034120/d034120171.png" />, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d034/d034120/d034120172.png" />, one defines the bilinear mapping
| |
| − | | |
| − | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d034/d034120/d034120173.png" /></td> <td valign="top" style="width:5%;text-align:right;">(*)</td></tr></table>
| |
| − | | |
| − | which may be written as the composition of a <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d034/d034120/d034120174.png" />-multiplication
| |
| − | | |
| − | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d034/d034120/d034120175.png" /></td> </tr></table>
| |
| − | | |
| − | (<img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d034/d034120/d034120176.png" /> denotes the family of compact supports) and linear forms <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d034/d034120/d034120177.png" /> on <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d034/d034120/d034120178.png" />, known as traces, of the form
| |
| − | | |
| − | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d034/d034120/d034120179.png" /></td> </tr></table>
| |
| − | | |
| − | where <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d034/d034120/d034120180.png" /> is the form of type <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d034/d034120/d034120181.png" /> with compact support which corresponds to the class <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d034/d034120/d034120182.png" /> by virtue of Dolbeault's theorem (cf. [[Differential form|Differential form]]). Serre's duality theorem states that if the cohomology spaces are endowed with a canonical locally convex topology (cf. [[Coherent analytic sheaf|Coherent analytic sheaf]]), then the mapping (*) is continuous with respect to the first argument and, if the space <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d034/d034120/d034120183.png" /> is separable, it defines an isomorphism of vector spaces
| |
| − | | |
| − | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d034/d034120/d034120184.png" /></td> </tr></table>
| |
| − | | |
| − | The roles of the sheaves <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d034/d034120/d034120185.png" /> and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d034/d034120/d034120186.png" /> may be interchanged, since the operation <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d034/d034120/d034120187.png" /> on locally free sheaves is involutory.
| |
| − | | |
| − | In particular, if the manifold <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d034/d034120/d034120188.png" /> is compact, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d034/d034120/d034120189.png" /> is the canonical and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d034/d034120/d034120190.png" /> is an arbitrary [[Divisor|divisor]] on <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d034/d034120/d034120191.png" />, Serre's theorem implies the equality of the dimensions of the spaces <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d034/d034120/d034120192.png" /> and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d034/d034120/d034120193.png" />, which is often used in computations with cohomology. A similar duality theorem is known for non-singular projective algebraic varieties over an arbitrary field (see Duality in algebraic geometry).
| |
| − | | |
| − | If <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d034/d034120/d034120194.png" /> is an arbitrary coherent analytic sheaf on the manifold <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d034/d034120/d034120195.png" />, there exists a real topological duality between the individual spaces associated with the topological vector spaces <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d034/d034120/d034120196.png" /> and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d034/d034120/d034120197.png" />, where <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d034/d034120/d034120198.png" /> is the family of closed supports, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d034/d034120/d034120199.png" /> is the family of compact supports, or vice versa, while the <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d034/d034120/d034120200.png" /> denote the derived functor (cf. [[Derived functor|Derived functor]]) of the functor <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d034/d034120/d034120201.png" />. The space <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d034/d034120/d034120202.png" /> is separable if <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d034/d034120/d034120203.png" /> is separable, and vice versa [[#References|[2]]], [[#References|[3]]]. This implies, for a compact manifold <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d034/d034120/d034120204.png" />, an isomorphism of finite-dimensional spaces
| |
| − | | |
| − | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d034/d034120/d034120205.png" /></td> </tr></table>
| |
| − | | |
| − | If <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d034/d034120/d034120206.png" /> is a [[Stein manifold|Stein manifold]], one obtains topological duality between <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d034/d034120/d034120207.png" /> and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d034/d034120/d034120208.png" />, and also between <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d034/d034120/d034120209.png" /> and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d034/d034120/d034120210.png" />.
| |
| − | | |
| − | There also exists a generalization of these results to the case of complex spaces with singularities [[#References|[4]]] and to the relative case [[#References|[5]]], in analogy to the corresponding duality theorems in algebraic geometry.
| |
| − | | |
| − | The following duality theorem is an analogue of Lefschetz's theorem [[#References|[3]]]: Let <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d034/d034120/d034120211.png" /> be a complex manifold of dimension <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d034/d034120/d034120212.png" /> with a countable base; let <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d034/d034120/d034120213.png" /> be a Stein compactum in <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d034/d034120/d034120214.png" />. For any coherent analytic sheaf <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d034/d034120/d034120215.png" /> on <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d034/d034120/d034120216.png" /> and any integer <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d034/d034120/d034120217.png" /> the space <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d034/d034120/d034120218.png" /> has a topology of type DFS (is strongly dual to a Fréchet–Schwartz space), and its dual space is algebraically isomorphic to <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d034/d034120/d034120219.png" />. According to another theorem of this type [[#References|[6]]], under the same assumptions, if <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d034/d034120/d034120220.png" /> is open, the space <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d034/d034120/d034120221.png" /> has a topology of type QFS (is a Fréchet–Schwartz quotient space), <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d034/d034120/d034120222.png" /> has a topology of type QDFS (is a quotient space of type DFS), while the associated separable spaces are in topological duality. The space <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d034/d034120/d034120223.png" /> is separable if and only if <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d034/d034120/d034120224.png" /> is.
| |
| − | | |
| − | The third type of duality theorem is represented by the following duality theorem [[#References|[8]]]: For any open subset <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d034/d034120/d034120225.png" />, the strong dual to the space <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d034/d034120/d034120226.png" /> is isomorphic to <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d034/d034120/d034120227.png" />. This theorem may be generalized as follows [[#References|[7]]]: Let <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d034/d034120/d034120228.png" /> be an <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d034/d034120/d034120229.png" />-dimensional complex manifold, countable at infinity, let <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d034/d034120/d034120230.png" /> be open, let <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d034/d034120/d034120231.png" /> be a coherent analytic sheaf on <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d034/d034120/d034120232.png" />, and let <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d034/d034120/d034120233.png" /> be an integer. Consider canonical mappings of topological vector spaces
| |
| − | | |
| − | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d034/d034120/d034120234.png" /></td> </tr></table>
| |
| − | | |
| − | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d034/d034120/d034120235.png" /></td> </tr></table>
| |
| − | | |
| − | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d034/d034120/d034120236.png" /></td> </tr></table>
| |
| − | | |
| − | For the separable space associated with <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d034/d034120/d034120237.png" /> to be isomorphic to the strong dual of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d034/d034120/d034120238.png" />, it is necessary and sufficient for <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d034/d034120/d034120239.png" /> to be closed. (An example of a non-closed <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d034/d034120/d034120240.png" /> is known.) In particular, if the sheaf <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d034/d034120/d034120241.png" /> is locally free and if
| |
| − | | |
| − | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d034/d034120/d034120242.png" /></td> </tr></table>
| |
| − | | |
| − | then the separable spaces associated with <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d034/d034120/d034120243.png" /> and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d034/d034120/d034120244.png" /> are in duality.
| |
| − | | |
| − | | |
| − | | |
| − | =====References=====
| |
| − | | |
| − | <table>
| |
| − | <TR><TD valign="top">[1]</TD> <TD valign="top"> J.-P. Serre, "Une théorème de dualité" ''Comm. Math. Helv.'' , '''29''' (1955) pp. 9–26 {{MR|}} {{ZBL|}} </TD></TR>
| |
| − | <TR><TD valign="top">[2]</TD> <TD valign="top"> B. Malgrange, "Systèmes differentiels à coefficients constants" , ''Sem. Bourbaki'' , '''246''' , Benjamin (1962–1963) {{MR|1611532}} {{MR|0304381}} {{MR|0176211}} {{ZBL|0229.35015}} {{ZBL|0141.27304}} {{ZBL|0231.46073}} </TD></TR>
| |
| − | <TR><TD valign="top">[3]</TD> <TD valign="top"> C. Banica, O. Stanasila, "Algebraic methods in the global theory of complex spaces" , Wiley (1976) (Translated from Rumanian) {{MR|0463470}} {{ZBL|0334.32001}} </TD></TR>
| |
| − | <TR><TD valign="top">[4]</TD> <TD valign="top"> J.P. Ramis, G. Ruget, "Complex dualisantet théorèmes de dualité en géométrie algébrique complexe" ''Publ. Math. IHES'' , '''38''' (1970) pp. 77–91 {{MR|}} {{ZBL|}} </TD></TR>
| |
| − | <TR><TD valign="top">[5]</TD> <TD valign="top"> J.P. Ramis, G. Ruget, "Résidus et dualité" ''Invent. Math.'' , '''26''' : 2 (1974) pp. 89–131 {{MR|0352522}} {{ZBL|0304.32007}} </TD></TR>
| |
| − | <TR><TD valign="top">[6]</TD> <TD valign="top"> V.D. Golovin, "On spaces of local cohomologies of complex analytic manifolds" ''Funct. Anal. Appl.'' , '''5''' : 4 (1971) pp. 320–322 ''Funktsional. Anal. Prilozhen.'' , '''5''' : 4 (1971) pp. 66 {{MR|}} {{ZBL|0242.32009}} </TD></TR>
| |
| − | <TR><TD valign="top">[7]</TD> <TD valign="top"> V.D. Golovin, "Alexander–Pontryagin duality in complex analysis" ''Math. Notes'' , '''13''' : 4 (1973) pp. 339–341 ''Mat. Zam.'' , '''13''' : 4 (1973) pp. 561–564 {{MR|}} {{ZBL|0271.32007}} </TD></TR>
| |
| − | <TR><TD valign="top">[8]</TD> <TD valign="top"> A. Grothendieck, "Sur certains espaces de fonctions holomorphes" ''J. Reine Agew. Math.'' , '''192''' (1953) pp. 35–64 {{MR|0062335}} {{MR|0058865}} {{ZBL|0051.08704}} </TD></TR>
| |
| − | </table>
| |
| − | | |
| − | | |
| − | | |
| − | ====Duality in analytic function theory (by A.I. Markushevich and S.Ya. Khavinson)====
| |
| − | | |
| − | =====Borel transforms=====
| |
| − | | |
| − | E. Borel (1895) must be credited with the idea of transforming a series
| |
| − | | |
| − | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d034/d034120/d034120245.png" /></td> </tr></table>
| |
| − | | |
| − | into the series
| |
| − | | |
| − | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d034/d034120/d034120246.png" /></td> </tr></table>
| |
| − | | |
| − | and conversely, under the condition that
| |
| − | | |
| − | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d034/d034120/d034120247.png" /></td> </tr></table>
| |
| − | | |
| − | This is a duality relation between functions which are analytic in a neighbourhood of infinity <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d034/d034120/d034120248.png" /> and entire functions of exponential type <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d034/d034120/d034120249.png" />. For instance, Pólya's theorem is obtained in this manner: Let <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d034/d034120/d034120250.png" /> be the supporting function of the convex envelope of the set of singularities of a function <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d034/d034120/d034120251.png" /> under analytic continuation to a half-plane of the form <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d034/d034120/d034120252.png" />, and let
| |
| − | | |
| − | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d034/d034120/d034120253.png" /></td> </tr></table>
| |
| − | | |
| − | be the growth indicator of the entire function <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d034/d034120/d034120254.png" />; then
| |
| − | | |
| − | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d034/d034120/d034120255.png" /></td> </tr></table>
| |
| − | | |
| − | By virtue of this duality relation the problem of analytic continuation of the function <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d034/d034120/d034120256.png" /> to the disc <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d034/d034120/d034120257.png" /> is equivalent to the study of the growth of the corresponding entire function <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d034/d034120/d034120258.png" /> in different directions.
| |
| − | | |
| − | | |
| − | =====Duality in spaces of analytic functions=====
| |
| − | | |
| − | Let <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d034/d034120/d034120259.png" /> be an open set in the extended complex plane <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d034/d034120/d034120260.png" /> and let <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d034/d034120/d034120261.png" /> be the space of analytic functions in <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d034/d034120/d034120262.png" /> with topology defined by the system of norms
| |
| − | | |
| − | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d034/d034120/d034120263.png" /></td> </tr></table>
| |
| − | | |
| − | where <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d034/d034120/d034120264.png" /> is an increasing system of compact sets contained in <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d034/d034120/d034120265.png" /> and exhausting <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d034/d034120/d034120266.png" />; thus, the convergence <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d034/d034120/d034120267.png" /> in <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d034/d034120/d034120268.png" /> means uniform convergence <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d034/d034120/d034120269.png" /> on all compact subsets of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d034/d034120/d034120270.png" />. Let <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d034/d034120/d034120271.png" />, let <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d034/d034120/d034120272.png" /> be the subspace of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d034/d034120/d034120273.png" /> of functions for which <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d034/d034120/d034120274.png" /> and let <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d034/d034120/d034120275.png" /> be a compact subset of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d034/d034120/d034120276.png" />. Consider the system <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d034/d034120/d034120277.png" /> of all open sets <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d034/d034120/d034120278.png" /> and the set of functions <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d034/d034120/d034120279.png" />. Two functions <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d034/d034120/d034120280.png" /> and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d034/d034120/d034120281.png" /> in this set are considered to be equivalent if their restrictions to some set <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d034/d034120/d034120282.png" /> coincide. The equivalence relation introduced subdivides the entire set under consideration into classes <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d034/d034120/d034120283.png" />. Each class is said to be a local analytic function on <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d034/d034120/d034120284.png" />, and the set of such functions is denoted by <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d034/d034120/d034120285.png" />. The class <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d034/d034120/d034120286.png" /> is naturally converted into a linear space, with the topology of the inductive limit of sequences of normed spaces <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d034/d034120/d034120287.png" /> introduced on it. This space is constructed as follows. Let <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d034/d034120/d034120288.png" /> be a decreasing sequence in <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d034/d034120/d034120289.png" /> such that <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d034/d034120/d034120290.png" /> and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d034/d034120/d034120291.png" />,
| |
| − | | |
| − | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d034/d034120/d034120292.png" /></td> </tr></table>
| |
| − | | |
| − | Now <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d034/d034120/d034120293.png" /> is the space of bounded analytic functions in <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d034/d034120/d034120294.png" /> with norm
| |
| − | | |
| − | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d034/d034120/d034120295.png" /></td> </tr></table>
| |
| − | | |
| − | The simplest fact about the duality of spaces of analytic functions is the following. Let <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d034/d034120/d034120296.png" /> be an open set, let (for the sake of being specific) <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d034/d034120/d034120297.png" />, and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d034/d034120/d034120298.png" />. The space <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d034/d034120/d034120299.png" /> is dual (conjugate) to the space <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d034/d034120/d034120300.png" /> in the sense of the theory of linear topological spaces. This duality is established as follows: If <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d034/d034120/d034120301.png" /> is a continuous linear functional on <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d034/d034120/d034120302.png" />, then there exists a unique element <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d034/d034120/d034120303.png" /> such that
| |
| − | | |
| − | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d034/d034120/d034120304.png" /></td> </tr></table>
| |
| − | | |
| − | where <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d034/d034120/d034120305.png" /> is some (composite) contour lying in <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d034/d034120/d034120306.png" /> and including <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d034/d034120/d034120307.png" />, while <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d034/d034120/d034120308.png" />, and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d034/d034120/d034120309.png" /> does not depend on <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d034/d034120/d034120310.png" />. The spaces <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d034/d034120/d034120311.png" /> may be defined for arbitrary sets <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d034/d034120/d034120312.png" />, and not only for the cases considered here, when <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d034/d034120/d034120313.png" /> is an open set and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d034/d034120/d034120314.png" /> is a compactum. Other generalizations include the consideration of sets on Riemann surfaces, spaces of functions of several complex variables and spaces of vector-valued analytic functions (with values in linear topological spaces).
| |
| − | | |
| − | The development of the duality theory of spaces of analytic functions was stimulated by the development of the general theory of duality of linear topological spaces and was itself a stimulus to the development of this theory by revealing deep specific relations. The applications of the duality theory of spaces of analytic functions are many, including problems of interpolation and approximation (see below), analytic continuation, subdivision and elimination of sets of singularities, and integral representations of various classes of functions.
| |
| − | | |
| − | | |
| − | =====Duality between completeness and uniqueness theorems=====
| |
| − | | |
| − | A system of elements <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d034/d034120/d034120315.png" /> of a locally convex space <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d034/d034120/d034120316.png" /> is complete if and only if, for an arbitrary linear functional <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d034/d034120/d034120317.png" /> continuous on <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d034/d034120/d034120318.png" />, it follows from <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d034/d034120/d034120319.png" />, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d034/d034120/d034120320.png" /> that <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d034/d034120/d034120321.png" />. This fact forms the connection between completeness problems in spaces of analytic functions and various uniqueness theorems for analytic functions. The functional <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d034/d034120/d034120322.png" /> is connected (cf. b) above) with some analytic function <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d034/d034120/d034120323.png" />. The condition <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d034/d034120/d034120324.png" />, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d034/d034120/d034120325.png" /> renders <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d034/d034120/d034120326.png" /> equal to zero at certain points or else renders the coefficients of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d034/d034120/d034120327.png" /> equal to zero. The uniqueness theorems lead to the conclusion that <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d034/d034120/d034120328.png" />, so that <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d034/d034120/d034120329.png" /> as well. The following duality principle of uniqueness and completeness problems has been formulated for spaces of analytic functions in a disc. Let <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d034/d034120/d034120330.png" /> and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d034/d034120/d034120331.png" /> be, respectively, the spaces of functions which are analytic in the discs <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d034/d034120/d034120332.png" /> and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d034/d034120/d034120333.png" />, where <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d034/d034120/d034120334.png" />, and let <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d034/d034120/d034120335.png" /> be a function which is analytic in the bicylinder <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d034/d034120/d034120336.png" />, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d034/d034120/d034120337.png" />. Let <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d034/d034120/d034120338.png" /> and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d034/d034120/d034120339.png" /> be linear functionals defined on <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d034/d034120/d034120340.png" /> and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d034/d034120/d034120341.png" />, and let <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d034/d034120/d034120342.png" /> and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d034/d034120/d034120343.png" /> be subsets of functions which can be represented, respectively, as <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d034/d034120/d034120344.png" /> and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d034/d034120/d034120345.png" />. A sequence of functions <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d034/d034120/d034120346.png" /> is complete in <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d034/d034120/d034120347.png" /> if and only if for each <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d034/d034120/d034120348.png" /> it follows from <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d034/d034120/d034120349.png" />, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d034/d034120/d034120350.png" /> that <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d034/d034120/d034120351.png" />. In particular, if <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d034/d034120/d034120352.png" /> and if <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d034/d034120/d034120353.png" />, both sets <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d034/d034120/d034120354.png" /> and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d034/d034120/d034120355.png" /> coincide with the set of all entire functions of exponential type.
| |
| − | | |
| − | | |
| − | =====Duality in extremal problems of the theory of functions=====
| |
| − | | |
| − | It is known that the problems of best approximation in normed spaces are dually connected with certain linear extremal problems. Thus, if <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d034/d034120/d034120356.png" /> is a subspace in a normed space <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d034/d034120/d034120357.png" /> and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d034/d034120/d034120358.png" /> is an arbitrary element of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d034/d034120/d034120359.png" />, one has
| |
| − | | |
| − | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d034/d034120/d034120360.png" /></td> <td valign="top" style="width:5%;text-align:right;">(1)</td></tr></table>
| |
| − | | |
| − | where <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d034/d034120/d034120361.png" /> is the annihilator of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d034/d034120/d034120362.png" />, i.e. the totality of linear functionals <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d034/d034120/d034120363.png" /> which vanish on the elements of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d034/d034120/d034120364.png" />. Relation (1), which is based on the [[Hahn–Banach theorem|Hahn–Banach theorem]], subsequently proved to be a special case of duality relations between extremal problems of mathematical programming. Let <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d034/d034120/d034120365.png" /> be an <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d034/d034120/d034120366.png" />-connected domain whose boundary <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d034/d034120/d034120367.png" /> consists of rectifiable contours, let <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d034/d034120/d034120368.png" /> be the class of analytic functions <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d034/d034120/d034120369.png" /> in <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d034/d034120/d034120370.png" />, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d034/d034120/d034120371.png" />, let <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d034/d034120/d034120372.png" /> be the class of analytic functions in <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d034/d034120/d034120373.png" /> which may be represented by the Cauchy integral over their boundary values, and let <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d034/d034120/d034120374.png" /> be some integrable function on <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d034/d034120/d034120375.png" />. Then:
| |
| − | | |
| − | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d034/d034120/d034120376.png" /></td> <td valign="top" style="width:5%;text-align:right;">(2)</td></tr></table>
| |
| − | | |
| − | The left-hand side of this equation is a linear extremal problem for bounded functions (e.g. if <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d034/d034120/d034120377.png" />, the resulting problem is <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d034/d034120/d034120378.png" />, i.e. the problem of Schwarz's lemma in a multiply-connected domain). The right-hand side of the equation is the problem of the best approximation of an arbitrary function <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d034/d034120/d034120379.png" /> on <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d034/d034120/d034120380.png" /> by boundary values of analytic functions in the integral metric. Relation (2) serves as the starting point for penetrating into each one of these two extremal problems involved: It serves to establish the characteristic properties of the extremal functions <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d034/d034120/d034120381.png" /> and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d034/d034120/d034120382.png" />, the problem of their uniqueness, etc. The function <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d034/d034120/d034120383.png" /> proves to have important geometric properties: In the problem of the Schwarz lemma it maps <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d034/d034120/d034120384.png" /> onto an <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d034/d034120/d034120385.png" />-sheeted disc; in other problems with an <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d034/d034120/d034120386.png" /> which is analytic on <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d034/d034120/d034120387.png" />, the function <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d034/d034120/d034120388.png" /> maps <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d034/d034120/d034120389.png" /> into an <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d034/d034120/d034120390.png" />-sheeted disc [[#References|[1]]]–[[#References|[6]]].
| |
| − | | |
| − | | |
| − | | |
| − | =====References=====
| |
| − | | |
| − | <table>
| |
| − | <TR><TD valign="top">[1]</TD> <TD valign="top"> A.I. Markushevitch, "Selected chapters on the theory of analytic functions" , Moscow (1976) (In Russian) {{MR|}} {{ZBL|}} </TD></TR>
| |
| − | <TR><TD valign="top">[2]</TD> <TD valign="top"> V.P. Khavin, "Spaces of analytic functions" ''Itogi Nauk. Mat. Anal. 1964'' (1966) pp. 76–164 (In Russian) {{MR|1771750}} {{MR|0776964}} {{ZBL|0601.30055}} {{ZBL|0151.08702}} </TD></TR>
| |
| − | <TR><TD valign="top">[3]</TD> <TD valign="top"> ''Itogi Nauk. Mat. Anal. 1967'' (1969) pp. 75–132</TD></TR>
| |
| − | <TR><TD valign="top">[4]</TD> <TD valign="top"> ''Itogi Nauk. Mat. Anal. 1963'' (1965) pp. 5–80</TD></TR>
| |
| − | <TR><TD valign="top">[5]</TD> <TD valign="top"> A.I. Markushevitch [A.I. Markushevich] (ed.) , ''Fonctions d'une variable complexe. Problème contemporains'' , Gauthier-Villars (1962) (Translated from Russian) {{MR|}} {{ZBL|}} </TD></TR>
| |
| − | <TR><TD valign="top">[6]</TD> <TD valign="top"> S.Ya. Khavinson, "Two papers on extremal problems in complex analysis" ''Transl. Amer. Math. Soc. (2)'' , '''129''' (1986) (Translated from Russian) {{MR|}} {{ZBL|}} </TD></TR>
| |
| − | </table>
| |
| − | | |
| − | ====Duality in the theory of topological vector spaces (by N.K. Nikol'skii)====
| |
| − | | |
| − | A dual pairing is a triplet <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d034/d034120/d034120391.png" /> in which <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d034/d034120/d034120392.png" /> are vector spaces over a field <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d034/d034120/d034120393.png" />, and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d034/d034120/d034120394.png" /> is a bilinear functional (form) on <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d034/d034120/d034120395.png" /> which has the property of being non-degenerate (or separating): If <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d034/d034120/d034120396.png" /> for each <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d034/d034120/d034120397.png" />, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d034/d034120/d034120398.png" />, then <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d034/d034120/d034120399.png" />; if <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d034/d034120/d034120400.png" /> for each <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d034/d034120/d034120401.png" />, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d034/d034120/d034120402.png" />, then <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d034/d034120/d034120403.png" />. One also says that <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d034/d034120/d034120404.png" /> realizes the duality and that <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d034/d034120/d034120405.png" /> form a dual pair; if <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d034/d034120/d034120406.png" /> is fixed, one writes <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d034/d034120/d034120407.png" />. The most important example is the natural duality: <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d034/d034120/d034120408.png" /> is a locally convex topological vector space with the topology <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d034/d034120/d034120409.png" />, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d034/d034120/d034120410.png" /> is the dual space (cf. [[Adjoint space|Adjoint space]]) of all linear <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d034/d034120/d034120411.png" />-continuous functionals on <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d034/d034120/d034120412.png" /> and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d034/d034120/d034120413.png" /> if <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d034/d034120/d034120414.png" />, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d034/d034120/d034120415.png" />; the fact that this form is non-degenerate is a consequence of, for example, the local convexity of the topology <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d034/d034120/d034120416.png" /> (a corollary of the [[Hahn–Banach theorem|Hahn–Banach theorem]]). The main subject of duality theory are methods for constructing objects in <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d034/d034120/d034120417.png" /> or <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d034/d034120/d034120418.png" /> which are dual to given ones with respect to the form <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d034/d034120/d034120419.png" />; the correspondence between the properties of mutually dual objects; and the topologies generated by the duality. The principal tool in these studies is the apparatus of polars; if <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d034/d034120/d034120420.png" /> or <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d034/d034120/d034120421.png" />, the polar of a set <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d034/d034120/d034120422.png" />, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d034/d034120/d034120423.png" />, is the set
| |
| − | | |
| − | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d034/d034120/d034120424.png" /></td> </tr></table>
| |
| − | | |
| − | The duality generates various locally convex topologies on <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d034/d034120/d034120425.png" /> (and also on <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d034/d034120/d034120426.png" /> ); for instance, the weak topology <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d034/d034120/d034120427.png" /> (generated by a given duality), specified by the family of semi-norms <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d034/d034120/d034120428.png" />, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d034/d034120/d034120429.png" />, is the weakest topology for which all the mappings <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d034/d034120/d034120430.png" /> are continuous; the Mackey topology <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d034/d034120/d034120431.png" />, with a neighbourhood base of zero formed by the polars <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d034/d034120/d034120432.png" /> of the absolutely convex <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d034/d034120/d034120433.png" />-compact subsets <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d034/d034120/d034120434.png" /> in <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d034/d034120/d034120435.png" />; and the strong topology <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d034/d034120/d034120436.png" />, a base of which is formed by the polars of the bounded subsets <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d034/d034120/d034120437.png" /> in <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d034/d034120/d034120438.png" />. For any <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d034/d034120/d034120439.png" />, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d034/d034120/d034120440.png" />, the set <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d034/d034120/d034120441.png" /> is the convex <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d034/d034120/d034120442.png" />-closed hull of the set <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d034/d034120/d034120443.png" /> (the bipolar theorem). The space <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d034/d034120/d034120444.png" /> is identical with <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d034/d034120/d034120445.png" /> (the basic theorem of duality theory which proves that any duality may be interpreted as natural). The space <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d034/d034120/d034120446.png" /> is said to be the weak conjugate (or dual) of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d034/d034120/d034120447.png" />.
| |
| − | | |
| − | Let <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d034/d034120/d034120448.png" /> be a locally convex space over <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d034/d034120/d034120449.png" /> or <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d034/d034120/d034120450.png" />. Each one of the following conditions is necessary and sufficient for a set <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d034/d034120/d034120451.png" />, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d034/d034120/d034120452.png" />, to be bounded: a) <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d034/d034120/d034120453.png" /> is bounded in the weak topology; and b) <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d034/d034120/d034120454.png" /> is an absorbing set. If <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d034/d034120/d034120455.png" /> is a neighbourhood of zero, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d034/d034120/d034120456.png" /> is <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d034/d034120/d034120457.png" />-compact. A metric space <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d034/d034120/d034120458.png" /> is complete if and only if a set <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d034/d034120/d034120459.png" />, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d034/d034120/d034120460.png" />, is closed in the topology <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d034/d034120/d034120461.png" /> whenever all intersections <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d034/d034120/d034120462.png" /> are closed in the same topology, where <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d034/d034120/d034120463.png" /> runs through the set of neighbourhoods of zero in <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d034/d034120/d034120464.png" /> (Krein–Shmul'yan theorem). If <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d034/d034120/d034120465.png" /> is a complete separable space and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d034/d034120/d034120466.png" /> is a linear functional on <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d034/d034120/d034120467.png" />, then <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d034/d034120/d034120468.png" /> if and only if <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d034/d034120/d034120469.png" /> in the topology <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d034/d034120/d034120470.png" /> implies that <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d034/d034120/d034120471.png" /> (Grothendieck's theorem). A subset <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d034/d034120/d034120472.png" /> of a complete space <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d034/d034120/d034120473.png" /> is relatively <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d034/d034120/d034120474.png" />-compact if it is relatively <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d034/d034120/d034120475.png" />-sequentially compact (Eberlein's theorem). A convex subset <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d034/d034120/d034120476.png" /> of a Fréchet space over <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d034/d034120/d034120477.png" /> is <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d034/d034120/d034120478.png" />-compact if and only if for any <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d034/d034120/d034120479.png" /> there exists an <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d034/d034120/d034120480.png" /> such that <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d034/d034120/d034120481.png" /> (James' theorem). <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d034/d034120/d034120482.png" /> is the finest and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d034/d034120/d034120483.png" /> is the coarsest among the topologies <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d034/d034120/d034120484.png" /> for which <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d034/d034120/d034120485.png" /> (the Mackey–Arens theorem, which yields a description of duality-preserving topologies of importance in applications). Each one of the following conditions concerning the space <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d034/d034120/d034120486.png" /> suffices for <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d034/d034120/d034120487.png" /> to coincide with the Mackey topology: a) <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d034/d034120/d034120488.png" /> is a [[Barrelled space|barrelled space]]; and b) <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d034/d034120/d034120489.png" /> is a bornological space (in particular, a metric space). The strong topology <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d034/d034120/d034120490.png" />, generally speaking, does not preserve the duality; if <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d034/d034120/d034120491.png" /> is locally convex and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d034/d034120/d034120492.png" />, the space <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d034/d034120/d034120493.png" /> is said to be the strong dual of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d034/d034120/d034120494.png" />, and if, in addition, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d034/d034120/d034120495.png" /> preserves the duality (i.e. if <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d034/d034120/d034120496.png" />), the space <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d034/d034120/d034120497.png" /> is said to be semi-reflexive (<img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d034/d034120/d034120498.png" /> is a [[Reflexive space|reflexive space]] if <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d034/d034120/d034120499.png" />).
| |
| − | | |
| − | Let <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d034/d034120/d034120500.png" /> be a subspace of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d034/d034120/d034120501.png" />; <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d034/d034120/d034120502.png" /> and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d034/d034120/d034120503.png" /> will then be dual pairs with respect to natural factorizations of the form <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d034/d034120/d034120504.png" />. If a family of dualities <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d034/d034120/d034120505.png" /> is given, the duality of the product space <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d034/d034120/d034120506.png" /> and the subspace <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d034/d034120/d034120507.png" /> is realized by the form
| |
| − | | |
| − | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d034/d034120/d034120508.png" /></td> </tr></table>
| |
| − | | |
| − | where
| |
| − | | |
| − | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d034/d034120/d034120509.png" /></td> </tr></table>
| |
| − | | |
| − | The dualities of the inductive and the projective limits <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d034/d034120/d034120510.png" />, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d034/d034120/d034120511.png" /> are described in a similar manner. The presence of duality-preserving topologies in the spaces <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d034/d034120/d034120512.png" />, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d034/d034120/d034120513.png" /> makes it possible to interpret these statements as the description of natural dualities for <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d034/d034120/d034120514.png" /> (the Tikhonov topology), <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d034/d034120/d034120515.png" /> (the quotient topology), <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d034/d034120/d034120516.png" /> (the induced topology), <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d034/d034120/d034120517.png" /> and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d034/d034120/d034120518.png" />, respectively. In the case of a normed space <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d034/d034120/d034120519.png" /> the natural isomorphism of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d034/d034120/d034120520.png" /> and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d034/d034120/d034120521.png" /> is an isometry
| |
| − | | |
| − | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d034/d034120/d034120522.png" /></td> </tr></table>
| |
| − | | |
| − | The use of duality in specific problems of linear analysis is proportional to the role played in such problems by linear (continuous) functionals. Especially essential (and possibly even crucial) are the ideas of duality theory in the following branches of analysis: in the study of linear topological (metric) properties of locally convex spaces and, in particular, the description of the natural duality for a given space [[#References|[1]]], [[#References|[2]]], [[#References|[3]]], [[#References|[5]]]; in the theory of generalized functions ; in the theory of extremal problems [[#References|[6]]], [[#References|[7]]]; in the spectral and structure theory of linear operators [[#References|[1]]], [[#References|[2]]]; in the completeness and uniqueness theorems in the theory of analytic functions; in the Fantappié theory of analytic functionals [[#References|[8]]]; see also Duality in analytic function theory.
| |
| − | | |
| − | | |
| − | | |
| − | =====References=====
| |
| − | | |
| − | <table>
| |
| − | <TR><TD valign="top">[1]</TD> <TD valign="top"> N. Bourbaki, "Elements of mathematics. Topological vector spaces" , Addison-Wesley (1977) (Translated from French) {{MR|0583191}} {{ZBL|1106.46003}} {{ZBL|1115.46002}} {{ZBL|0622.46001}} {{ZBL|0482.46001}} </TD></TR>
| |
| − | <TR><TD valign="top">[2]</TD> <TD valign="top"> W.J. Robertson, "Topological vector spaces" , Cambridge Univ. Press (1964) {{MR|0162118}} {{ZBL|0123.30202}} </TD></TR>
| |
| − | <TR><TD valign="top">[3]</TD> <TD valign="top"> H.H. Schaefer, "Topological vector spaces" , Macmillan (1966) {{MR|0193469}} {{ZBL|0141.30503}} </TD></TR>
| |
| − | <TR><TD valign="top">[4]</TD> <TD valign="top"> N. Dunford, J.T. Schwartz, "Linear operators" , '''1–3''' , Interscience (1958–1971) {{MR|1009164}} {{MR|1009163}} {{MR|1009162}} {{MR|0412888}} {{MR|0216304}} {{MR|0188745}} {{MR|0216303}} {{MR|1530651}} {{MR|0117523}} {{ZBL|0635.47003}} {{ZBL|0635.47002}} {{ZBL|0635.47001}} {{ZBL|0283.47002}} {{ZBL|0243.47001}} {{ZBL|0146.12601}} {{ZBL|0128.34803}} {{ZBL|0084.10402}} </TD></TR>
| |
| − | <TR><TD valign="top">[5]</TD> <TD valign="top"> M.M. Day, "Normed linear spaces" , Springer (1958) {{MR|0094675}} {{ZBL|0082.10603}} </TD></TR>
| |
| − | <TR><TD valign="top">[6]</TD> <TD valign="top"> A.D. Ioffe, V.M. Tikhomirov, "Theory of extremal problems" , North-Holland (1979) (Translated from Russian) {{MR|0528295}} {{MR|0527119}} {{ZBL|0407.90051}} </TD></TR>
| |
| − | <TR><TD valign="top">[7]</TD> <TD valign="top"> R.T. Rockafellar, "Convex analysis" , Princeton Univ. Press (1970) {{MR|0274683}} {{ZBL|0193.18401}} </TD></TR>
| |
| − | <TR><TD valign="top">[8]</TD> <TD valign="top"> V.P. Khavin, "Spaces of analytic functions" ''Itogi Nauk. Mat. Anal. 1964'' (1966) pp. 76–164 (In Russian) {{MR|1771750}} {{MR|0776964}} {{ZBL|0601.30055}} {{ZBL|0151.08702}} </TD></TR>
| |
| − | <TR><TD valign="top">[9]</TD> <TD valign="top"> S.Ya. Khavinson, "Extremal problems for bounded analytic functions with interior side conditions" ''Russian Math. Surveys'' , '''18''' (1963) pp. 23–96 ''Uspekhi Mat. Nauk'' , '''18''' : 2 (1963) pp. 25–98 {{MR|}} {{ZBL|0149.03302}} </TD></TR>
| |
| − | <TR><TD valign="top">[10]</TD> <TD valign="top"> J. Diestel, "Geometry of Banach spaces - selected topics" , Springer (1975) {{MR|0461094}} {{ZBL|0307.46009}} </TD></TR>
| |
| − | </table>
| |
| − | | |
| − | | |
| − | | |
| − | =====Comments=====
| |
| − | There is a well-used topology on the dual <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d034/d034120/d034120523.png" /> of a topological vector space <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d034/d034120/d034120524.png" />: the weak-<img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d034/d034120/d034120526.png" />-topology. It is the weakest topology on <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d034/d034120/d034120527.png" /> in which all mappings <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d034/d034120/d034120528.png" />, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d034/d034120/d034120529.png" />, are continuous.
| |
| − | | |
| − | | |
| − | | |
| − | ====Duality in extremal problems and convex analysis (by V.M. Tikhomirov)====
| |
| − | | |
| − | A property of convex sets, convex functions and convex extremal problems, viz. that they can be posed in a dual manner — in the basic and in the dual (conjugate) spaces. Closed convex sets in a locally convex topological vector space may be described in a dual way: they are identical with the intersection of the closed half-spaces which contain them. This makes it possible for any convex set <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d034/d034120/d034120530.png" /> in a vector space <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d034/d034120/d034120531.png" /> to be connected with a dual object in the conjugate space — its polar <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d034/d034120/d034120532.png" />. Closed convex functions (i.e. functions with convex and closed supergraphs) in a locally convex topological vector space also permit a dual description (cf. also [[Dual functions|Dual functions]]; [[Conjugate function|Conjugate function]]): they are pointwise least upper bounds of the affine functions which do not exceed them in size. Such a duality permits one to establish a connection between a convex function <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d034/d034120/d034120533.png" /> and the dual object — the conjugate function given on the conjugate space <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d034/d034120/d034120534.png" /> and defined by the formula
| |
| − | | |
| − | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d034/d034120/d034120535.png" /></td> </tr></table>
| |
| − | | |
| − | Pointwise least upper bounds of linear functions in a locally convex topological vector space are convex closed homogeneous functions. This fact forms the base for the duality between convex sets and convex homogeneous functions. The dualities just described are based on the [[Hahn–Banach theorem|Hahn–Banach theorem]] about the extension of linear functionals and the theorem of separability of convex sets.
| |
| − | | |
| − | The meaning of the dual specification of convex sets and convex functions is reflected in the involutory nature of the polar operator <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d034/d034120/d034120536.png" /> and the conjugation operator <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d034/d034120/d034120537.png" />, which exists for convex closed sets containing zero and convex closed functions which are everywhere larger than <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d034/d034120/d034120538.png" />. This last result, which concerns functions (the Fenchel–Moreau theorem), generates many duality theorems for the extremal problems of linear and convex programming. An example of a pair of dual problems in linear programming is the following:
| |
| | | | |
| − | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d034/d034120/d034120539.png" /></td> <td valign="top" style="width:5%;text-align:right;">(1)</td></tr></table>
| + | [[Arrangement of hyperplanes|Hyperplane arrangements]]: The number of regions in a central arrangement of hyperplanes is given by $t ( M _ { H } ; 2,0 )$, where $M _ { H }$ is the matroid associated with the arrangement. Many generalizations of this result appear in [[#References|[a15]]]. |
| | | | |
| − | Here
| + | [[Combinatorial topology]]: The independent subsets of a matroid form a [[shellable complex]]. If $h _ { M } ( x )$ is the shelling polynomial associated with this complex, then $h _ { M } ( x ) = t ( x , 1 )$ and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t120/t120210/t12021074.png"/>. This result is analogous to the dichromatic interpretation for planar graphs. See [[#References|[a1]]] for more information on how the Tutte polynomial is associated to simplicial complexes. |
| | | | |
| − | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d034/d034120/d034120540.png" /></td> </tr></table>
| + | [[Statistical mechanics, mathematical problems in|Statistical mechanics]], network reliability and [[knot theory]]: Suppose $M$ is a probabilistic matroid, i.e., each $e \in E$ has an independent probability $p ( e )$ of successful operation. The formula |
| | | | |
| − | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d034/d034120/d034120541.png" /></td> </tr></table>
| + | \begin{equation*} t ( M ; x , y ) = \sum _ { S \subseteq E } \left( \prod _ { e \in S } p ( e ) \right) \left( \prod _ { e \notin S } ( 1 - p ( e ) ) \right)\times \end{equation*} |
| | | | |
| − | The following alternative is valid for a pair of dual problems in linear programming: The values of the problems are either finite and equal and both problems have a solution, or else the set of permissible values of one of the problems is empty or the solution of the problem equals infinity. The usual method for constructing a dual problem is as follows. The problem of minimization:
| + | \begin{equation*} \times ( x - 1 ) ^ { r ( M ) - r ( S ) } ( y - 1 ) ^ { | S | - r ( s )} \end{equation*} |
| | | | |
| − | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d034/d034120/d034120542.png" /></td> <td valign="top" style="width:5%;text-align:right;">(2)</td></tr></table>
| + | then produces a probabilistic Tutte polynomial. In this more general situation, $t ( M ; 1,2 )$ is the reliability of $M$, i.e., the probability that a randomly chosen subset spans $E$. Related Tutte polynomials have applications in statistical mechanics and network reliability [[#References|[a5]]] and knot theory [[#References|[a11]]]. |
| | | | |
| − | where <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d034/d034120/d034120543.png" /> is a linear space, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d034/d034120/d034120544.png" />, is included in a class of similar problems which depend on a parameter:
| + | [[Greedoid]]s: When $G$ is a greedoid (cf. also [[Greedy algorithm|Greedy algorithm]]), the expansion $t ( G ; x , y ) = \sum_{ S \subseteq E} ( x - 1 ) ^ { r ( G ) - r ( S ) } ( y - 1 ) ^ { | S | - r ( S ) }$ remains valid. The recursion of T3) takes a slightly different form, however: If $e$ is feasible, then $t ( G ) = t ( G / e ) + ( x - 1 ) ^ { r ( G ) - r ( G - e ) } t ( G - e )$. There are many combinatorial structures which admit a greedoid rank function in a natural way, but do not possess a meaningful matroid structure. For example, if $T _ { 1 }$ and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t120/t120210/t12021088.png"/> are [[rooted tree]]s (cf. also [[Tree]]), then computing the Tutte polynomial in this way gives $t ( T _ { 1 } ) = t ( T _ { 2 } )$ if and only if $T _ { 1 }$ and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t120/t120210/t12021091.png"/> are isomorphic as rooted trees [[#References|[a8]]]. |
| | | | |
| − | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d034/d034120/d034120545.png" /></td> </tr></table>
| + | In general, it is $\cal N P$-hard (cf. [[NP|$\cal N P$]]) to compute the Tutte polynomial of a graph or a matroid [[#References|[a10]]]. Certain evaluations are computable in polynomial-time for certain classes of matroids, however. For example, the number of spanning trees of a graph can be calculated in polynomial-time by the matrix-tree theorem; since this number equals $t ( M ; 1,1 )$, this evaluation is tractable. |
| − | | |
| − | where <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d034/d034120/d034120546.png" /> is some other linear space, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d034/d034120/d034120547.png" />, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d034/d034120/d034120548.png" /> (the function <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d034/d034120/d034120549.png" /> is known as a perturbation of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d034/d034120/d034120550.png" />). As a rule, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d034/d034120/d034120551.png" /> is assumed to be convex. The problem which is dual to the problem in relation to a given perturbation is the problem
| |
| − | | |
| − | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d034/d034120/d034120552.png" /></td> <td valign="top" style="width:5%;text-align:right;">(2ast)</td></tr></table>
| |
| − | | |
| − | where <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d034/d034120/d034120553.png" /> is the function dual to (conjugate with) <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d034/d034120/d034120554.png" /> in the sense of Legendre–Young–Fenchel (cf. [[Dual functions|Dual functions]]). For the simplest problems in convex programming, of the type
| |
| − | | |
| − | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d034/d034120/d034120555.png" /></td> <td valign="top" style="width:5%;text-align:right;">(3)</td></tr></table>
| |
| − | | |
| − | where <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d034/d034120/d034120556.png" /> is a linear space, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d034/d034120/d034120557.png" /> are convex functions on <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d034/d034120/d034120558.png" /> and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d034/d034120/d034120559.png" /> is a convex set in <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d034/d034120/d034120560.png" /> (linear programming problems are special cases of (3)), the following standard perturbations, which depend on the parameters <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d034/d034120/d034120561.png" />, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d034/d034120/d034120562.png" />, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d034/d034120/d034120563.png" />, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d034/d034120/d034120564.png" />, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d034/d034120/d034120565.png" />, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d034/d034120/d034120566.png" />, are usually employed. The duality theorems for the general classes of linear problems state that, if certain assumptions regarding the perturbation <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d034/d034120/d034120567.png" /> are made, the values of the problems (2) and (2ast) coincide and, in addition, the solution of one of the problems is a Lagrange multiplier for the other.
| |
| − | | |
| − | | |
| − | | |
| − | =====References=====
| |
| | | | |
| | + | ====References==== |
| | <table> | | <table> |
| − | <TR><TD valign="top">[1]</TD> <TD valign="top"> H. Minkowski, "Geometrie der Zahlen" , Chelsea, reprint (1953) {{MR|0249269}} {{ZBL|0050.04807}} </TD></TR> | + | <tr><td valign="top">[a1]</td> <td valign="top"> A. Björner, "The homology and shellability of matroids and geometric lattices" N. White (ed.) , ''Matroid Applications'' , ''Encycl. Math. Appl.'' , '''40''' , Cambridge Univ. Press (1992) pp. 226–283</td></tr> |
| − | <TR><TD valign="top">[2]</TD> <TD valign="top"> H. Minkowski, , ''Gesammelte Abhandlungen'' , '''1–2''' , Teubner (1911) {{MR|}} {{ZBL|42.0023.03}} </TD></TR> | + | <tr><td valign="top">[a2]</td> <td valign="top"> T.H. Brylawski, "The Tutte–Grothendieck ring" ''Algebra Univ.'' , '''2''' (1972) pp. 375–388</td></tr> |
| − | <TR><TD valign="top">[3]</TD> <TD valign="top"> W. Fenchel, "On conjugate convex functions" ''Canad. J. Math.'' , '''1''' (1949) pp. 73–77 {{MR|0028365}} {{ZBL|0038.20902}} </TD></TR> | + | <tr><td valign="top">[a3]</td> <td valign="top"> T.H. Brylawski, "The Tutte polynomial. Part 1: General theory" A. Barlotti (ed.) , ''Matroid Theory and its Applications Proc. Third Mathematics Summer Center C.I.M.E.'' , Liguori, Naples (1980) pp. 125–275</td></tr> |
| − | <TR><TD valign="top">[4]</TD> <TD valign="top"> R.T. Rockafellar, "Convex analysis" , Princeton Univ. Press (1970) {{MR|0274683}} {{ZBL|0193.18401}} </TD></TR> | + | <tr><td valign="top">[a4]</td> <td valign="top"> T.H. Brylawski, J.G. Oxley, "The Tutte polynomial and its applications" N. White (ed.) , ''Matroid Applications'' , ''Encycl. Math. Appl.'' , '''40''' , Cambridge Univ. Press (1992) pp. 123–225</td></tr> |
| − | <TR><TD valign="top">[5]</TD> <TD valign="top"> I. Ekeland, R. Téman, "Analyse convexe et problèmes variationnels" , Dunod (1974) {{MR|0463993}} {{MR|0463994}} {{ZBL|0281.49001}} </TD></TR> | + | <tr><td valign="top">[a5]</td> <td valign="top"> C.J. Colbourn, "The combinatorics of network reliability" , Oxford Univ. Press (1987)</td></tr> |
| − | <TR><TD valign="top">[6]</TD> <TD valign="top"> A.D. Ioffe, V.M. Tikhomirov, "Theory of extremal problems" , North-Holland (1979) (Translated from Russian) {{MR|0528295}} {{MR|0527119}} {{ZBL|0407.90051}} </TD></TR> | + | <tr><td valign="top">[a6]</td> <td valign="top"> H.H. Crapo, "The Tutte polynomial" ''Aequat. Math.'' , '''3''' (1969) pp. 211–229</td></tr> |
| | + | <tr><td valign="top">[a7]</td> <td valign="top"> H.H. Crapo, G.-C. Rota, "On the foundations of combinatorial theory: Combinatorial geometries" , MIT (1970) (Edition: Preliminary)</td></tr> |
| | + | <tr><td valign="top">[a8]</td> <td valign="top"> G.P. Gordon, E.W. McMahon, "A greedoid polynomial which distinguishes rooted arborescences" ''Proc. Amer. Math. Soc.'' , '''107''' (1989) pp. 287–298</td></tr> |
| | + | <tr><td valign="top">[a9]</td> <td valign="top"> C. Greene, T. Zaslavsky, "On the interpretation of Whitney numbers through arrangements of hyperplanes, zonotopes, non–Radon partitions, and orientations of graphs" ''Trans. Amer. Math. Soc.'' , '''280''' (1983) pp. 97–126</td></tr> |
| | + | <tr><td valign="top">[a10]</td> <td valign="top"> F. Jaeger, D.L. Vertigan, D.J.A. Welsh, "On the computational complexity of the Jones and Tutte polynomials" ''Math. Proc. Cambridge Philos. Soc.'' , '''108''' (1990) pp. 35–53</td></tr> |
| | + | <tr><td valign="top">[a11]</td> <td valign="top"> L. Kauffman, "Knots and physics" , World Sci. (1993) (Edition: Second)</td></tr> |
| | + | <tr><td valign="top">[a12]</td> <td valign="top"> J.P.S. Kung, "Critical problems" J. Bonin (ed.) et al. (ed.) , ''Matroid Theory'' , ''Contemp. Math.'' , '''197''' , Amer. Math. Soc. (1996) pp. 1–128</td></tr> |
| | + | <tr><td valign="top">[a13]</td> <td valign="top"> R.P. Stanley, "Acyclic orientations of graphs" ''Discrete Math.'' , '''5''' (1973) pp. 171–178</td></tr> |
| | + | <tr><td valign="top">[a14]</td> <td valign="top"> W.T. Tutte, "A contribution to the theory of chromatic polynomials" ''Canad. J. Math.'' , '''6''' (1954) pp. 80–91</td></tr> |
| | + | <tr><td valign="top">[a15]</td> <td valign="top"> T. Zaslavsky, "Facing up to arrangements: Face-count formulas for partitions of space by hyperplanes" ''Memoirs Amer. Math. Soc.'' , '''154''' (1975)</td></tr> |
| | + | <tr><td valign="top">[a16]</td> <td valign="top"> T. Zaslavsky, "The Möbius functions and the characteristic polynomial" N. White (ed.) , ''Combinatorial Geometries'' , ''Encycl. Math. Appl.'' , '''29''' , Cambridge Univ. Press (1987) pp. 114–138</td></tr> |
| | </table> | | </table> |
| − |
| |
| − |
| |
| − |
| |
| − | ====Duality of finite Abelian groups (by A.I. Kostrikin)====
| |
| − |
| |
| − | The classical prototype of general [[Pontryagin duality]] and of its various subsequent modifications. It concerns the properties of the isomorphic correspondence between a finite Abelian group $A$ and the group $\hat{A}=Hom(A,k^*)$ of its characters with values in the [[multiplicative group]] $k^*$ of an algebraically closed field $k$ of a characteristic which does not divide the order of $A$ (cf. [[Character group]]). The natural mapping
| |
| − | $$
| |
| − | f\colon A\to \hat{\hat{A}}
| |
| − | $$
| |
| − | defined by the rule
| |
| − | $$
| |
| − | f(a)(\chi)=\chi(a)
| |
| − | $$
| |
| − | for all $a\in A$, $\chi\in\hat{A}$, is also an isomorphism, while for any subgroup $B\subseteq A$ one has $f(B)=(B^\perp)^\perp$, where
| |
| − | $$
| |
| − | B^\perp=\{\chi\in\hat{A}\colon\chi(b)=1\quad\text{for all}\quad b\in B\}\cong\widehat{A/B}.
| |
| − | $$
| |
| − | The correspondence $B\to B^\perp$ establishes a duality between the lattices of subgroups of $A$ and $\hat{A}$. This is a one-to-one correspondence and it has the properties
| |
| − | $$
| |
| − | (BC)^\perp=B^\perp\cap C^\perp,\quad (B\cap C)^\perp=B^\perp C^\perp.
| |
| − | $$
| |
| − |
| |
| − |
| |
| − |
| |
| − | =====References=====
| |
| − |
| |
| − | <table>
| |
| − | <TR><TD valign="top">[1]</TD> <TD valign="top"> L.S. Pontryagin, "Topological groups" , Princeton Univ. Press (1958) (Translated from Russian) {{MR|0201557}} {{ZBL|0022.17104}} </TD></TR>
| |
| − | <TR><TD valign="top">[2]</TD> <TD valign="top"> B. Huppert, "Endliche Gruppen" , '''1''' , Springer (1979) pp. 482–490 {{MR|0224703}} {{ZBL|0412.20002}} </TD></TR>
| |
| − | </table>
| |
| − |
| |
| − |
| |
| − |
| |
| − | =====Comments=====
| |
| − |
| |
| − | Duality is a very pervasive and important concept in (modern) mathematics. Besides in various articles mentioned above such as [[Alexander duality]]; [[Kolmogorov duality]]; [[Lefschetz duality]]; [[S-duality]], still more duality-type material can be found in the articles [[Hypergraph]] (dual hypergraph), [[Graph, planar]] (dual graph), [[Algebra of logic]] (duality principle in logic, dual operations), [[Induced representation]] (Frobenius reciprocity or duality), [[Projective plane]] and [[Projective space]] (duality principle in projective geometry), [[Duality principle]] (in geometry and in logic), [[Linear programming]] (dual linear programs and the dual simplex method), [[Unitary representation]] (the dual space of irreducible representations of a group), [[Partially ordered set]] (same set with opposite order), [[Thom space]] (for Atiyah's S-duality theorem), [[Dual category]]; [[Pontryagin duality]] (also for Tanaka–Krein duality), [[Topological vector space]] (for more on duality of locally convex spaces), [[Symmetric space]] (a duality between symmetric Riemannian homogeneous spaces of noncompact type and of compact type), [[Formal group]] (Cartier duality between formal groups and commutative unipotent algebraic groups), [[Steenrod duality]] (cohomological), [[Convex set]] (duality of convex bodies), [[Code with correction of arithmetical errors]] (for the idea of a dual code), [[Vector space]] (dual vector space and dual linear operator), [[Adjoint module]].
| |
| − |
| |
| − | Let $\hat{A}$ denote the [[Picard variety]] (of linear divisor classes) of an [[Abelian variety]] $A$. Then the duality theorem for Abelian varieties states that $\hat{\hat{A}} = A$.
| |
Let $M$ be a matroid with rank function $r$ on the ground set $E$. The Tutte polynomial $t ( M ; x , y )$ of $M$ is defined by
\begin{equation*} t ( M ; x , y ) = \sum _ { S \subseteq E } ( x - 1 ) ^ { r ( M ) - r ( S ) } ( y - 1 ) ^ { | S | - r ( S )}. \end{equation*}
One also writes $t ( M )$ for $t ( M ; x , y )$ when no confusion can arise about the values of $x$ and $y$. There are several equivalent reformulations of $t ( M )$; the most useful such expression is recursive, using the matroid operations of deletion and contraction:
T0) If $E = \emptyset$, then $t ( M ) = 1$;
T1) If $e$ is an isthmus, then $t ( M ) = x t ( M / e )$;
T2) If $e$ is a loop, then $t ( M ) = y t ( M - e )$;
T3) If $e$ is neither an isthmus nor a loop, then $t ( M ) = t ( M / e ) + t ( M - e )$.
Some standard evaluations of the Tutte polynomial are:
a) $t ( M ; 1,1 )$ is the number of bases of $M$;
b) $t ( M ; 2,1 )$ is the number of independent subsets of $M$;
c) $t ( M ; 1,2 )$ is the number of spanning subsets of $M$;
d) $t ( M ; 2,2 ) = 2 ^ { | E | }$.
When a matroid $M$ is constructed from other matroids $M _ { 1 } , M _ { 2 } , \ldots$, it is frequently possible to compute $t ( M )$ from the $t ( M _ { i } )$. The most fundamental structural result of this kind concerns the direct sum of matroids: $t ( M _ { 1 } \oplus M _ { 2 } ) = t ( M _ { 1 } ) t ( M _ { 2 } )$. Another fundamental structural property of the Tutte polynomial is its transparent relationship with matroid duality: $t ( M ^ { * } ; x , y ) = t ( M ; y , x )$. Many related results can be found in [a3].
The Tutte polynomial has many significant connections with invariants in graph theory. Of central importance is the relationship between $t ( M )$ and the chromatic polynomial $\chi ( G ; \lambda )$ of a graph $G$ (cf. also Graph colouring). If $G$ is a graph having $v ( G )$ vertices and $c ( G )$ connected components, then
\begin{equation*} \chi ( G ; \lambda ) = \lambda ^ { c ( G ) } ( - 1 ) ^ { v ( G ) - c ( G ) } t ( M _ { G } , 1 - \lambda , 0 ), \end{equation*}
where $M _ { G }$ is the cycle matroid of $G$ (cf. also Matroid). Thus, when $G$ is planar (cf. Graph, planar), $t ( M _ { G } ; x , y )$ simultaneously carries information concerning proper colourings of $G$ along with proper colourings of its dual graph $G ^ { * }$. This is the reason W.T. Tutte referred to it as a dichromatic polynomial in his foundational work in this area [a14]. The polynomial was generalized from graphs to matroids by H.H. Crapo [a5] and T.H. Brylawski [a2].
Other invariants which can be obtained from the Tutte polynomial include the beta invariant $\beta ( M )$, the Möbius function $\mu ( M )$, and the characteristic polynomial $p ( M ; \lambda )$ of a matroid $M$. See [a16] for more information about these invariants.
Applications
The Tutte polynomial has applications in various areas, some of which are given below. For an extensive introduction, see [a4].
Acyclic orientations: Let $a ( G )$ denote the number of acyclic orientations of a graph $G$. Then R. Stanley [a13] proved that $a ( G ) = t ( M _ { G } ; 2,0 )$. A variety of related evaluations appear in [a9].
The critical problem of Crapo and G.-C. Rota [a7]: Let $M$ be a rank-$r$ matroid which is represented over $\operatorname {GF} ( q )$ by $\phi : E \rightarrow \operatorname {GF} ( q ) ^ { n }$ and let $k$ be a positive integer. Then the number of $k$-tuples of linear functionals on $\operatorname{GF} ( q ) ^ { n }$ which distinguish $\phi ( E )$ equals $( - 1 ) ^ { r } q ^ { k ( n - r ) } t ( M ; 1 - q ^ { k } , 0 )$. See [a12] for extensions of the critical problem.
Coding theory: Let $C$ be a linear code over $\operatorname {GF} ( q )$ with code-weight polynomial $A ( C ; q , z ) = \sum _ { \mathbf{v} \in C } z ^ { w (\mathbf{v}) }$, where $w ( \mathbf{v} )$ is the weight of the code word $\mathbf{v}$ (see also Coding and decoding). Then
\begin{equation*} A ( C , q , z ) = ( 1 - z ) ^ { r } z ^ { n - r } t \left( M _ { C } ; \frac { 1 + ( q - 1 ) z } { 1 - z } , \frac { 1 } { z } \right), \end{equation*}
where $M _ { C }$ is the matroid associated with the code $C$. Many standard results in coding theory have interpretations using the Tutte polynomial [a4].
Hyperplane arrangements: The number of regions in a central arrangement of hyperplanes is given by $t ( M _ { H } ; 2,0 )$, where $M _ { H }$ is the matroid associated with the arrangement. Many generalizations of this result appear in [a15].
Combinatorial topology: The independent subsets of a matroid form a shellable complex. If $h _ { M } ( x )$ is the shelling polynomial associated with this complex, then $h _ { M } ( x ) = t ( x , 1 )$ and 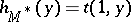 . This result is analogous to the dichromatic interpretation for planar graphs. See [a1] for more information on how the Tutte polynomial is associated to simplicial complexes.
. This result is analogous to the dichromatic interpretation for planar graphs. See [a1] for more information on how the Tutte polynomial is associated to simplicial complexes.
Statistical mechanics, network reliability and knot theory: Suppose $M$ is a probabilistic matroid, i.e., each $e \in E$ has an independent probability $p ( e )$ of successful operation. The formula
\begin{equation*} t ( M ; x , y ) = \sum _ { S \subseteq E } \left( \prod _ { e \in S } p ( e ) \right) \left( \prod _ { e \notin S } ( 1 - p ( e ) ) \right)\times \end{equation*}
\begin{equation*} \times ( x - 1 ) ^ { r ( M ) - r ( S ) } ( y - 1 ) ^ { | S | - r ( s )} \end{equation*}
then produces a probabilistic Tutte polynomial. In this more general situation, $t ( M ; 1,2 )$ is the reliability of $M$, i.e., the probability that a randomly chosen subset spans $E$. Related Tutte polynomials have applications in statistical mechanics and network reliability [a5] and knot theory [a11].
Greedoids: When $G$ is a greedoid (cf. also Greedy algorithm), the expansion $t ( G ; x , y ) = \sum_{ S \subseteq E} ( x - 1 ) ^ { r ( G ) - r ( S ) } ( y - 1 ) ^ { | S | - r ( S ) }$ remains valid. The recursion of T3) takes a slightly different form, however: If $e$ is feasible, then $t ( G ) = t ( G / e ) + ( x - 1 ) ^ { r ( G ) - r ( G - e ) } t ( G - e )$. There are many combinatorial structures which admit a greedoid rank function in a natural way, but do not possess a meaningful matroid structure. For example, if $T _ { 1 }$ and  are rooted trees (cf. also Tree), then computing the Tutte polynomial in this way gives $t ( T _ { 1 } ) = t ( T _ { 2 } )$ if and only if $T _ { 1 }$ and
are rooted trees (cf. also Tree), then computing the Tutte polynomial in this way gives $t ( T _ { 1 } ) = t ( T _ { 2 } )$ if and only if $T _ { 1 }$ and  are isomorphic as rooted trees [a8].
are isomorphic as rooted trees [a8].
In general, it is $\cal N P$-hard (cf. $\cal N P$) to compute the Tutte polynomial of a graph or a matroid [a10]. Certain evaluations are computable in polynomial-time for certain classes of matroids, however. For example, the number of spanning trees of a graph can be calculated in polynomial-time by the matrix-tree theorem; since this number equals $t ( M ; 1,1 )$, this evaluation is tractable.
References
| [a1] | A. Björner, "The homology and shellability of matroids and geometric lattices" N. White (ed.) , Matroid Applications , Encycl. Math. Appl. , 40 , Cambridge Univ. Press (1992) pp. 226–283 |
| [a2] | T.H. Brylawski, "The Tutte–Grothendieck ring" Algebra Univ. , 2 (1972) pp. 375–388 |
| [a3] | T.H. Brylawski, "The Tutte polynomial. Part 1: General theory" A. Barlotti (ed.) , Matroid Theory and its Applications Proc. Third Mathematics Summer Center C.I.M.E. , Liguori, Naples (1980) pp. 125–275 |
| [a4] | T.H. Brylawski, J.G. Oxley, "The Tutte polynomial and its applications" N. White (ed.) , Matroid Applications , Encycl. Math. Appl. , 40 , Cambridge Univ. Press (1992) pp. 123–225 |
| [a5] | C.J. Colbourn, "The combinatorics of network reliability" , Oxford Univ. Press (1987) |
| [a6] | H.H. Crapo, "The Tutte polynomial" Aequat. Math. , 3 (1969) pp. 211–229 |
| [a7] | H.H. Crapo, G.-C. Rota, "On the foundations of combinatorial theory: Combinatorial geometries" , MIT (1970) (Edition: Preliminary) |
| [a8] | G.P. Gordon, E.W. McMahon, "A greedoid polynomial which distinguishes rooted arborescences" Proc. Amer. Math. Soc. , 107 (1989) pp. 287–298 |
| [a9] | C. Greene, T. Zaslavsky, "On the interpretation of Whitney numbers through arrangements of hyperplanes, zonotopes, non–Radon partitions, and orientations of graphs" Trans. Amer. Math. Soc. , 280 (1983) pp. 97–126 |
| [a10] | F. Jaeger, D.L. Vertigan, D.J.A. Welsh, "On the computational complexity of the Jones and Tutte polynomials" Math. Proc. Cambridge Philos. Soc. , 108 (1990) pp. 35–53 |
| [a11] | L. Kauffman, "Knots and physics" , World Sci. (1993) (Edition: Second) |
| [a12] | J.P.S. Kung, "Critical problems" J. Bonin (ed.) et al. (ed.) , Matroid Theory , Contemp. Math. , 197 , Amer. Math. Soc. (1996) pp. 1–128 |
| [a13] | R.P. Stanley, "Acyclic orientations of graphs" Discrete Math. , 5 (1973) pp. 171–178 |
| [a14] | W.T. Tutte, "A contribution to the theory of chromatic polynomials" Canad. J. Math. , 6 (1954) pp. 80–91 |
| [a15] | T. Zaslavsky, "Facing up to arrangements: Face-count formulas for partitions of space by hyperplanes" Memoirs Amer. Math. Soc. , 154 (1975) |
| [a16] | T. Zaslavsky, "The Möbius functions and the characteristic polynomial" N. White (ed.) , Combinatorial Geometries , Encycl. Math. Appl. , 29 , Cambridge Univ. Press (1987) pp. 114–138 |
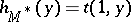 . This result is analogous to the dichromatic interpretation for planar graphs. See [a1] for more information on how the Tutte polynomial is associated to simplicial complexes.
. This result is analogous to the dichromatic interpretation for planar graphs. See [a1] for more information on how the Tutte polynomial is associated to simplicial complexes.
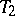 are rooted trees (cf. also Tree), then computing the Tutte polynomial in this way gives $t ( T _ { 1 } ) = t ( T _ { 2 } )$ if and only if $T _ { 1 }$ and
are rooted trees (cf. also Tree), then computing the Tutte polynomial in this way gives $t ( T _ { 1 } ) = t ( T _ { 2 } )$ if and only if $T _ { 1 }$ and 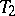 are isomorphic as rooted trees [a8].
are isomorphic as rooted trees [a8].