Difference between revisions of "Regularization of sequences"
(Importing text file) |
Ulf Rehmann (talk | contribs) m (tex encoded by computer) |
||
| Line 1: | Line 1: | ||
| − | + | <!-- | |
| + | r0809401.png | ||
| + | $#A+1 = 89 n = 2 | ||
| + | $#C+1 = 89 : ~/encyclopedia/old_files/data/R080/R.0800940 Regularization of sequences | ||
| + | Automatically converted into TeX, above some diagnostics. | ||
| + | Please remove this comment and the {{TEX|auto}} line below, | ||
| + | if TeX found to be correct. | ||
| + | --> | ||
| − | + | {{TEX|auto}} | |
| + | {{TEX|done}} | ||
| − | + | Let $ a _ {n} $, | |
| + | $ n = 0, 1 \dots $ | ||
| + | be a sequence of real numbers (indexed by the non-negative integers). A regularization of $ \{ a _ {n} \} $ | ||
| + | is a sequence $ \{ a _ {n} ^ {(} r) \} $ | ||
| + | obtained from $ \{ a _ {n} \} $ | ||
| + | by replacing certain $ a _ {n} $ | ||
| + | which are "excessively high" with respect to the others by suitable lower values. An important application of regularized sequences is to the problem of equivalence of classes of $ C ^ \infty $- | ||
| + | functions; that is, the problem of when two sequences of constants determine the same [[Quasi-analytic class|quasi-analytic class]] of functions. The answers tend to be given in the form that the two sequences $ \{ M _ {n} \} $ | ||
| + | and $ \{ L _ {n} \} $ | ||
| + | determine the same quasi-analytic class if suitably regularized sequences $ \{ M _ {n} ^ {(} r) \} $ | ||
| + | and $ \{ L _ {n} ^ {(} r) \} $ | ||
| + | are the same, cf. [[#References|[a1]]], [[#References|[a2]]]. | ||
| − | + | Some important regularization procedures are as follows. A sequence $ \{ a _ {n} \} $ | |
| + | of real numbers is called a convex sequence if the function $ n \mapsto a _ {n} $ | ||
| + | is convex, i.e. if for all $ 0\leq r < i < s $, | ||
| − | + | $$ | |
| + | a _ {i} \leq | ||
| + | \frac{i- r }{s- r } | ||
| + | a _ {s} + s- | ||
| + | \frac{i}{s-} | ||
| + | r a _ {r} ; | ||
| + | $$ | ||
| − | + | that is, if the point $ ( i, a _ {i} ) $ | |
| + | is located below or on the segment in the plane joining $ ( r, a _ {r} ) $ | ||
| + | and $ ( s, a _ {s} ) $( | ||
| + | cf. [[Convex function (of a real variable)|Convex function (of a real variable)]]). | ||
| − | + | The convex regularization, or Newton regularization, $ \{ a _ {n} ^ {(} c) \} $ | |
| + | of $ \{ a _ {n} \} $ | ||
| + | is the largest convex minorant of $ \{ a _ {n} \} $( | ||
| + | cf. [[Majorant and minorant|Majorant and minorant]], 1)). | ||
| − | The | + | The log-convex regularization, or convex regularization by means of the logarithm, of a sequence of positive numbers $ \{ a _ {n} \} $ |
| + | is the sequence of positive numbers $ \{ a _ {n} ^ {(} lc) \} $ | ||
| + | such that $ \{ \mathop{\rm log} a _ {n} ^ {(} lc) \} $ | ||
| + | is the convex regularization of $ \{ \mathop{\rm log} a _ {n} \} $. | ||
| + | It is defined by the relations | ||
| − | + | $$ | |
| + | T _ {a} ( r) = \sup _ { n> } 0 | ||
| + | \frac{r ^ {n} }{a _ {n} } | ||
| + | ,\ \ | ||
| + | a _ {n} ^ {(} lc) = \sup _ { r> } 0 | ||
| + | \frac{r ^ {n} }{T _ {a} ( r) } | ||
| + | . | ||
| + | $$ | ||
| − | The | + | The exponential regularization $ \{ a _ {n} ^ {(} e) \} $ |
| + | of $ \{ a _ {n} \} $ | ||
| + | is defined by the relations | ||
| − | + | $$ | |
| + | S _ {a} ( r) = = \max _ {n \leq r } | ||
| + | \frac{r ^ {n} }{a _ {n} } | ||
| + | \ ( r \geq 1) ,\ \ | ||
| + | a _ {n} ^ {(} e) = \sup _ {r \geq n } | ||
| + | \frac{r ^ {n} | ||
| + | }{S _ {a} ( r) } | ||
| + | . | ||
| + | $$ | ||
| + | |||
| + | The Newton regularization of a sequence $ \{ a _ {n} \} $ | ||
| + | is very much related to the Newton polygon of $ \{ a _ {n} \} $( | ||
| + | this explains the name "Newton regularization" , cf. also [[Newton diagram|Newton diagram]], which discusses the context in which the Newton polygon first arose). For a finite sequence $ \{ a _ {n} \} _ {n=} 0 ^ {N} $, | ||
| + | its Newton polygon is the highest convex polygonal line in $ \mathbf R ^ {2} $ | ||
| + | joining $ ( 0, a _ {0} ) $ | ||
| + | to $ ( N, a _ {N} ) $, | ||
| + | i.e. it is the polygonal line consisting of the segments joining $ ( i, a _ {i} ^ {(} c) ) $ | ||
| + | to $ ( i+ 1 , a _ {i+} 1 ^ {(} c) ) $, | ||
| + | $ i= 0 \dots N- 1 $. | ||
| + | Thus, the number $ a _ {i} ^ {(} c) $ | ||
| + | is the ordinate of the point of the Newton polygon of $ \{ a _ {i} \} $ | ||
| + | with abscissa $ i $. | ||
| + | |||
| + | An example of this for the sequence $ ( 1, 1, - 2, 1, - 4/3, 1/3, 0) $, | ||
| + | $ N= 6 $, | ||
| + | with convex regularization $ ( 1, - 1/2, - 2, - 5/3, - 4/3, - 2/3, 0) $, | ||
| + | is given in Fig. a. | ||
<img style="border:1px solid;" src="https://www.encyclopediaofmath.org/legacyimages/common_img/r080940a.gif" /> | <img style="border:1px solid;" src="https://www.encyclopediaofmath.org/legacyimages/common_img/r080940a.gif" /> | ||
| Line 25: | Line 97: | ||
Figure: r080940a | Figure: r080940a | ||
| − | To avoid certain pathologies (like | + | To avoid certain pathologies (like $ a _ {i} ^ {(} c) = - \infty $ |
| + | for all $ i > 0 $), | ||
| + | let $ \{ a _ {n} \} _ {n=} 0 ^ \infty $ | ||
| + | be bounded from below. The Newton polygon of this sequence is defined as the limit of the Newton polygons of the finite sequences $ \{ a _ {n} \} _ {n=} 0 ^ {N} $ | ||
| + | as $ N \rightarrow \infty $. | ||
| + | It remains true that $ a _ {i} ^ {(} c) $ | ||
| + | is determined by the condition that $ ( i, a _ {i} ^ {(} c) ) $ | ||
| + | lies on the Newton polygon of $ \{ a _ {n} \} _ {n=} 0 ^ \infty $. | ||
| − | Let | + | Let $ K $ |
| + | be a non-Archimedean valued field with [[Valuation|valuation]] $ v $( | ||
| + | cf. also [[Norm on a field|Norm on a field]]). Let $ 1+ a _ {1} X + \dots + a _ {N} X ^ {N} = f( X) $ | ||
| + | be a polynomial of degree $ N $ | ||
| + | over $ K $. | ||
| + | The Newton polygon of the polynomial $ f( X) $ | ||
| + | is the Newton polygon of the sequence $ ( v( 1), v( a _ {1} ) \dots v ( a _ {N} )) $. | ||
| + | It carries immediate information on the valuations of the roots of $ f( X) $( | ||
| + | in a complete algebraic closure of $ K $). | ||
| + | Indeed, if $ \lambda $ | ||
| + | is the slope of a segment of the Newton polygon of (abscissa) length $ r $, | ||
| + | then there are precisely $ r $ | ||
| + | roots of valuation $ - \lambda $( | ||
| + | counted with multiplicities); an analogous result holds for roots of power series (this is related to a $ p $- | ||
| + | adic Weierstrass preparation theorem, cf. (the editorial comments to) [[Weierstrass theorem|Weierstrass theorem]], and [[#References|[a3]]]). | ||
| − | The Newton polygon of a sequence | + | The Newton polygon of a sequence $ \{ a _ {n} \} $ |
| + | can be obtained geometrically as follows. For all $ t, c \in ( - \infty , \infty ) $ | ||
| + | one considers the line $ l( t, c) $ | ||
| + | in $ \mathbf R ^ {2} $ | ||
| + | through $ ( 0, c) $ | ||
| + | of slope $ t $; | ||
| + | it is given by the equation $ y= tx+ c $. | ||
| + | Let $ U( t, c)= \{ {( x, y) } : {x\geq 0, y\geq tx+ c } \} $ | ||
| + | be the [[Supergraph|supergraph]] of $ l( t, c) $. | ||
| + | Let $ A $ | ||
| + | be the graph of $ \{ a _ {n} \} $, | ||
| + | $ A= \{ {( i, a _ {i} ) } : {i= 0 , 1 ,\dots } \} $. | ||
| + | Then the Newton polygon is the lower boundary of the convex set | ||
| − | + | $$ | |
| + | \cap _ {A \subset U( t,c) } U( t, c). | ||
| + | $$ | ||
| − | As noted, the Newton regularization (convex regularization) of a sequence | + | As noted, the Newton regularization (convex regularization) of a sequence $ \{ a _ {n} \} $ |
| + | is determined by its Newton polygon. This construction has been generalized. Let $ \omega ( t) $ | ||
| + | be a non-decreasing function of $ t $ | ||
| + | with values in $ [ 0, \infty ] $. | ||
| + | Let | ||
| − | + | $$ | |
| + | U ^ \omega ( t, c) = U( t, c) \cup \{ {( x, y) } : {x > \omega ( t) } \} | ||
| + | . | ||
| + | $$ | ||
The lower boundary of | The lower boundary of | ||
| − | + | $$ | |
| + | \cap _ {A \subset U ^ \omega ( t,c) } U ^ \omega ( t, c) | ||
| + | $$ | ||
| − | now defines the | + | now defines the $ \omega $- |
| + | regularized sequence $ \{ a _ {n} ^ {( \omega ) } \} $. | ||
| + | Newton and exponential regularization correspond to $ \omega ( t) \equiv \infty $ | ||
| + | and $ \omega ( t) = \mathop{\rm exp} ( t) $, | ||
| + | respectively. | ||
====References==== | ====References==== | ||
<table><TR><TD valign="top">[a1]</TD> <TD valign="top"> S. Mandelbrojt, "Séries adhérentes, régularisations des suites, applications" , Gauthier-Villars (1952)</TD></TR><TR><TD valign="top">[a2]</TD> <TD valign="top"> J.A. Siddigi, "On the equivalence of classes of infinitely differentiable functions" ''Soviet J. Contemp. Math. Anal. Arm. Acad. Sci.'' , '''19''' : 1 (1984) pp. 18–29 ''Izv. Akad. Nauk Arm.SSR Mat.'' , '''19''' : 1 (1984) pp. 19–30</TD></TR><TR><TD valign="top">[a3]</TD> <TD valign="top"> N. Koblitz, "<img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r080/r080940/r08094091.png" />-adic numbers, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r080/r080940/r08094092.png" />-adic analysis, and zeta-functions" , Springer (1977) pp. Chapt. IV, §3–4</TD></TR></table> | <table><TR><TD valign="top">[a1]</TD> <TD valign="top"> S. Mandelbrojt, "Séries adhérentes, régularisations des suites, applications" , Gauthier-Villars (1952)</TD></TR><TR><TD valign="top">[a2]</TD> <TD valign="top"> J.A. Siddigi, "On the equivalence of classes of infinitely differentiable functions" ''Soviet J. Contemp. Math. Anal. Arm. Acad. Sci.'' , '''19''' : 1 (1984) pp. 18–29 ''Izv. Akad. Nauk Arm.SSR Mat.'' , '''19''' : 1 (1984) pp. 19–30</TD></TR><TR><TD valign="top">[a3]</TD> <TD valign="top"> N. Koblitz, "<img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r080/r080940/r08094091.png" />-adic numbers, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r080/r080940/r08094092.png" />-adic analysis, and zeta-functions" , Springer (1977) pp. Chapt. IV, §3–4</TD></TR></table> | ||
Revision as of 08:10, 6 June 2020
Let $ a _ {n} $,
$ n = 0, 1 \dots $
be a sequence of real numbers (indexed by the non-negative integers). A regularization of $ \{ a _ {n} \} $
is a sequence $ \{ a _ {n} ^ {(} r) \} $
obtained from $ \{ a _ {n} \} $
by replacing certain $ a _ {n} $
which are "excessively high" with respect to the others by suitable lower values. An important application of regularized sequences is to the problem of equivalence of classes of $ C ^ \infty $-
functions; that is, the problem of when two sequences of constants determine the same quasi-analytic class of functions. The answers tend to be given in the form that the two sequences $ \{ M _ {n} \} $
and $ \{ L _ {n} \} $
determine the same quasi-analytic class if suitably regularized sequences $ \{ M _ {n} ^ {(} r) \} $
and $ \{ L _ {n} ^ {(} r) \} $
are the same, cf. [a1], [a2].
Some important regularization procedures are as follows. A sequence $ \{ a _ {n} \} $ of real numbers is called a convex sequence if the function $ n \mapsto a _ {n} $ is convex, i.e. if for all $ 0\leq r < i < s $,
$$ a _ {i} \leq \frac{i- r }{s- r } a _ {s} + s- \frac{i}{s-} r a _ {r} ; $$
that is, if the point $ ( i, a _ {i} ) $ is located below or on the segment in the plane joining $ ( r, a _ {r} ) $ and $ ( s, a _ {s} ) $( cf. Convex function (of a real variable)).
The convex regularization, or Newton regularization, $ \{ a _ {n} ^ {(} c) \} $ of $ \{ a _ {n} \} $ is the largest convex minorant of $ \{ a _ {n} \} $( cf. Majorant and minorant, 1)).
The log-convex regularization, or convex regularization by means of the logarithm, of a sequence of positive numbers $ \{ a _ {n} \} $ is the sequence of positive numbers $ \{ a _ {n} ^ {(} lc) \} $ such that $ \{ \mathop{\rm log} a _ {n} ^ {(} lc) \} $ is the convex regularization of $ \{ \mathop{\rm log} a _ {n} \} $. It is defined by the relations
$$ T _ {a} ( r) = \sup _ { n> } 0 \frac{r ^ {n} }{a _ {n} } ,\ \ a _ {n} ^ {(} lc) = \sup _ { r> } 0 \frac{r ^ {n} }{T _ {a} ( r) } . $$
The exponential regularization $ \{ a _ {n} ^ {(} e) \} $ of $ \{ a _ {n} \} $ is defined by the relations
$$ S _ {a} ( r) = = \max _ {n \leq r } \frac{r ^ {n} }{a _ {n} } \ ( r \geq 1) ,\ \ a _ {n} ^ {(} e) = \sup _ {r \geq n } \frac{r ^ {n} }{S _ {a} ( r) } . $$
The Newton regularization of a sequence $ \{ a _ {n} \} $ is very much related to the Newton polygon of $ \{ a _ {n} \} $( this explains the name "Newton regularization" , cf. also Newton diagram, which discusses the context in which the Newton polygon first arose). For a finite sequence $ \{ a _ {n} \} _ {n=} 0 ^ {N} $, its Newton polygon is the highest convex polygonal line in $ \mathbf R ^ {2} $ joining $ ( 0, a _ {0} ) $ to $ ( N, a _ {N} ) $, i.e. it is the polygonal line consisting of the segments joining $ ( i, a _ {i} ^ {(} c) ) $ to $ ( i+ 1 , a _ {i+} 1 ^ {(} c) ) $, $ i= 0 \dots N- 1 $. Thus, the number $ a _ {i} ^ {(} c) $ is the ordinate of the point of the Newton polygon of $ \{ a _ {i} \} $ with abscissa $ i $.
An example of this for the sequence $ ( 1, 1, - 2, 1, - 4/3, 1/3, 0) $, $ N= 6 $, with convex regularization $ ( 1, - 1/2, - 2, - 5/3, - 4/3, - 2/3, 0) $, is given in Fig. a.
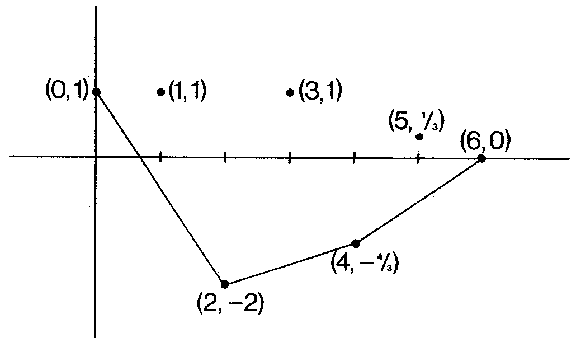
Figure: r080940a
To avoid certain pathologies (like $ a _ {i} ^ {(} c) = - \infty $ for all $ i > 0 $), let $ \{ a _ {n} \} _ {n=} 0 ^ \infty $ be bounded from below. The Newton polygon of this sequence is defined as the limit of the Newton polygons of the finite sequences $ \{ a _ {n} \} _ {n=} 0 ^ {N} $ as $ N \rightarrow \infty $. It remains true that $ a _ {i} ^ {(} c) $ is determined by the condition that $ ( i, a _ {i} ^ {(} c) ) $ lies on the Newton polygon of $ \{ a _ {n} \} _ {n=} 0 ^ \infty $.
Let $ K $ be a non-Archimedean valued field with valuation $ v $( cf. also Norm on a field). Let $ 1+ a _ {1} X + \dots + a _ {N} X ^ {N} = f( X) $ be a polynomial of degree $ N $ over $ K $. The Newton polygon of the polynomial $ f( X) $ is the Newton polygon of the sequence $ ( v( 1), v( a _ {1} ) \dots v ( a _ {N} )) $. It carries immediate information on the valuations of the roots of $ f( X) $( in a complete algebraic closure of $ K $). Indeed, if $ \lambda $ is the slope of a segment of the Newton polygon of (abscissa) length $ r $, then there are precisely $ r $ roots of valuation $ - \lambda $( counted with multiplicities); an analogous result holds for roots of power series (this is related to a $ p $- adic Weierstrass preparation theorem, cf. (the editorial comments to) Weierstrass theorem, and [a3]).
The Newton polygon of a sequence $ \{ a _ {n} \} $ can be obtained geometrically as follows. For all $ t, c \in ( - \infty , \infty ) $ one considers the line $ l( t, c) $ in $ \mathbf R ^ {2} $ through $ ( 0, c) $ of slope $ t $; it is given by the equation $ y= tx+ c $. Let $ U( t, c)= \{ {( x, y) } : {x\geq 0, y\geq tx+ c } \} $ be the supergraph of $ l( t, c) $. Let $ A $ be the graph of $ \{ a _ {n} \} $, $ A= \{ {( i, a _ {i} ) } : {i= 0 , 1 ,\dots } \} $. Then the Newton polygon is the lower boundary of the convex set
$$ \cap _ {A \subset U( t,c) } U( t, c). $$
As noted, the Newton regularization (convex regularization) of a sequence $ \{ a _ {n} \} $ is determined by its Newton polygon. This construction has been generalized. Let $ \omega ( t) $ be a non-decreasing function of $ t $ with values in $ [ 0, \infty ] $. Let
$$ U ^ \omega ( t, c) = U( t, c) \cup \{ {( x, y) } : {x > \omega ( t) } \} . $$
The lower boundary of
$$ \cap _ {A \subset U ^ \omega ( t,c) } U ^ \omega ( t, c) $$
now defines the $ \omega $- regularized sequence $ \{ a _ {n} ^ {( \omega ) } \} $. Newton and exponential regularization correspond to $ \omega ( t) \equiv \infty $ and $ \omega ( t) = \mathop{\rm exp} ( t) $, respectively.
References
| [a1] | S. Mandelbrojt, "Séries adhérentes, régularisations des suites, applications" , Gauthier-Villars (1952) |
| [a2] | J.A. Siddigi, "On the equivalence of classes of infinitely differentiable functions" Soviet J. Contemp. Math. Anal. Arm. Acad. Sci. , 19 : 1 (1984) pp. 18–29 Izv. Akad. Nauk Arm.SSR Mat. , 19 : 1 (1984) pp. 19–30 |
| [a3] | N. Koblitz, "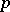 -adic numbers, -adic numbers, 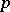 -adic analysis, and zeta-functions" , Springer (1977) pp. Chapt. IV, §3–4 -adic analysis, and zeta-functions" , Springer (1977) pp. Chapt. IV, §3–4 |
Regularization of sequences. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Regularization_of_sequences&oldid=19031