Difference between revisions of "L-space-of-a-statistical-experiment"
(Importing text file) |
Ulf Rehmann (talk | contribs) m (tex encoded by computer) |
||
| Line 1: | Line 1: | ||
| − | + | <!-- | |
| + | l1100302.png | ||
| + | $#A+1 = 99 n = 1 | ||
| + | $#C+1 = 99 : ~/encyclopedia/old_files/data/L110/L.1100030 \BMI L\EMI\AAhspace of a statistical experiment | ||
| + | Automatically converted into TeX, above some diagnostics. | ||
| + | Please remove this comment and the {{TEX|auto}} line below, | ||
| + | if TeX found to be correct. | ||
| + | --> | ||
| − | + | {{TEX|auto}} | |
| + | {{TEX|done}} | ||
| − | + | An order-complete [[Banach lattice|Banach lattice]] (cf. also [[Riesz space|Riesz space]]) of measures on a [[Measurable space|measurable space]] $ ( \Omega, {\mathcal F} ) $, | |
| + | defined in the context of [[Statistical decision theory|statistical decision theory]] [[#References|[a2]]], [[#References|[a5]]], [[#References|[a7]]], [[#References|[a8]]], [[#References|[a10]]]. Prime object of this theory is the statistical experiment $ {\mathcal E} = ( \Omega, {\mathcal F}, {\mathcal P} ) $ | ||
| + | where $ {\mathcal P} $ | ||
| + | is a set of probability measures on $ ( \Omega, {\mathcal F} ) $. | ||
| + | A statistical decision problem is to determine which of the distributions in $ {\mathcal P} $ | ||
| + | are most likely to generate the observations (or data) collected. While the [[Radon–Nikodým theorem|Radon–Nikodým theorem]] guarantees that one can operate with densities | ||
| − | + | $$ | |
| + | { | ||
| + | \frac{dP }{d \mu } | ||
| + | } \in L _ {1} ( \mu ) | ||
| + | $$ | ||
| − | + | of distributions if all $ P \in {\mathcal P} $ | |
| + | are dominated by a $ \sigma $- | ||
| + | finite measure $ \mu $ | ||
| + | on $ ( \Omega, {\mathcal F} ) $, | ||
| + | there is no such possibility in the undominated case. Nevertheless, there is a substitute for the space generated by the $ { {dP } / {d \mu } } $ | ||
| + | which respects both the linear and the order structure of measures: the $ L $- | ||
| + | space $ L ( {\mathcal E} ) $ | ||
| + | of the experiment, introduced in [[#References|[a4]]]. This is a subspace of the Banach lattice of all signed measures on $ ( \Omega, {\mathcal F} ) $, | ||
| + | and can be defined in three different ways, as follows [[#References|[a1]]]. | ||
| − | + | Denote by $ { \mathop{\rm ca} } ( \Omega, {\mathcal F} ) $ | |
| + | the vector lattice of all signed finite measures on $ ( \Omega, {\mathcal F} ) $, | ||
| + | put $ | \mu | = \sup ( \mu, - \mu ) \in { \mathop{\rm ca} } ( \Omega, {\mathcal F} ) $ | ||
| + | and use $ \mu \perp \nu $ | ||
| + | as an abbreviation for $ \inf ( | \mu | , | \nu | ) = 0 $. | ||
| + | Equipped with the variational norm $ \| \mu \| = | \mu | ( \Omega ) $, | ||
| + | $ { \mathop{\rm ca} } ( \Omega, {\mathcal F} ) $ | ||
| + | is an order-complete Banach lattice. More precisely, $ { \mathop{\rm ca} } ( \Omega, {\mathcal F} ) $ | ||
| + | is an abstract $ L $- | ||
| + | space, which means that the norm $ \| \cdot \| $ | ||
| + | is additive on $ { \mathop{\rm ca} } ( \Omega, {\mathcal F} ) _ {+} $. | ||
| + | A solid linear subspace $ {\mathcal D} \subseteq { \mathop{\rm ca} } ( \Omega, {\mathcal F} ) $ | ||
| + | is called a band if $ \sup _ {i \in I } \mu _ {i} \in {\mathcal D} $ | ||
| + | whenever the $ \mu _ {i} \in {\mathcal D} $ | ||
| + | satisfy $ \mu _ {i} \leq \mu \in { \mathop{\rm ca} } ( \Omega, {\mathcal F} ) $ | ||
| + | for all $ i \in I $. | ||
| − | + | If $ {\mathcal E} = ( \Omega, {\mathcal F}, {\mathcal P} ) $ | |
| + | is a statistical experiment, then one defines | ||
| − | + | a) $ L _ {1} ( {\mathcal E} ) $ | |
| + | to be the smallest band (with respect to $ \subseteq $) | ||
| + | in $ { \mathop{\rm ca} } ( \Omega, {\mathcal F} ) $ | ||
| + | containing $ {\mathcal P} $; | ||
| − | + | b) $ L _ {2} ( {\mathcal E} ) $ | |
| + | to be the $ \| \cdot \| $- | ||
| + | closure of $ L ^ \prime ( {\mathcal E} ) $, | ||
| + | where | ||
| − | + | $$ | |
| + | L ^ \prime ( {\mathcal E} ) = \left \{ {\mu \in { \mathop{\rm ca} } ( \Omega, {\mathcal F} ) } : \left | \mu \right | \leq \sum _ {i = 1 } ^ { n } \alpha _ {i} P _ {i} \right . | ||
| + | $$ | ||
| − | + | $$ | |
| + | \left . | ||
| + | {\textrm{ for some } P _ {i} \in {\mathcal P}, \alpha _ {i} \geq 0, \textrm{ all } i ; n \in \mathbf N } \right \} ; | ||
| + | $$ | ||
| − | + | c) $ L _ {3} ( {\mathcal E} ) = \{ {\mu \in { \mathop{\rm ca} } ( \Omega, {\mathcal F} ) } : {\mu \perp \sigma \textrm{ for all } \sigma \perp {\mathcal P} } \} $. | |
| + | Then $ L _ {1} ( {\mathcal E} ) = L _ {2} ( {\mathcal E} ) = L _ {3} ( {\mathcal E} ) $. | ||
| + | This space is called the $ L $- | ||
| + | space of $ {\mathcal E} $ | ||
| + | and is denoted by $ L ( {\mathcal E} ) $. | ||
| − | + | If there exists a $ Q \in { \mathop{\rm ca} } ( \Omega, {\mathcal F} ) $ | |
| + | such that for $ A \in {\mathcal F} $ | ||
| + | one has $ Q ( A ) = 0 $ | ||
| + | if and only if $ P ( A ) = 0 $ | ||
| + | for all $ P \in {\mathcal P} $, | ||
| + | then $ {\mathcal E} $ | ||
| + | is dominated (and vice versa). In this case, the $ L $- | ||
| + | space $ L ( {\mathcal E} ) $ | ||
| + | of $ {\mathcal E} $ | ||
| + | is, as a Banach lattice, isomorphic to $ L ^ {1} ( Q ) $. | ||
| + | The situation for undominated experiments is different. As an abstract $ L $- | ||
| + | space, $ L ( {\mathcal E} ) $ | ||
| + | is always isomorphic to $ L ^ {1} ( m ) $, | ||
| + | with $ m $ | ||
| + | a [[Radon measure|Radon measure]] on a locally compact topological space [[#References|[a3]]]. However, in general $ m $ | ||
| + | is not even semi-finite [[#References|[a6]]] (i.e., lacks the finite subset property [[#References|[a11]]]), and then there is no representation of the topological dual $ M ( {\mathcal E} ) = L ( {\mathcal E} ) ^ {*} $ | ||
| + | as $ L ^ \infty ( m ) $. | ||
| + | $ M ( {\mathcal E} ) $ | ||
| + | is called the $ M $- | ||
| + | space of the experiment $ {\mathcal E} $ | ||
| + | and generalizes the space of equivalence classes of bounded random variables in the following sense. Let $ X $ | ||
| + | denote the set of all real-valued functions defined on $ \Omega $ | ||
| + | that are $ {\mathcal F} $- | ||
| + | measurable and bounded. For any $ \varphi \in X $, | ||
| + | denote by $ {\dot \varphi } $ | ||
| + | the mapping assigning $ \int _ \Omega \varphi {d \mu } $ | ||
| + | to every $ \mu \in L ( {\mathcal E} ) $. | ||
| + | Then $ M ( {\mathcal E} ) $ | ||
| + | coincides with the $ \sigma ( M ( {\mathcal E} ) ,L ( {\mathcal E} ) ) $- | ||
| + | closure of $ {\dot{X} } $[[#References|[a1]]], [[#References|[a4]]], [[#References|[a8]]]. For an alternative representation of $ M ( {\mathcal E} ) $, | ||
| + | see [[#References|[a9]]]. | ||
| + | |||
| + | An experiment $ {\mathcal E} $ | ||
| + | is called coherent if $ M ( {\mathcal E} ) = {\dot{X} } $. | ||
| + | Every dominated experiment is also coherent, due to the familiar isomorphism between $ [ L ^ {1} ( Q ) ] ^ {*} $ | ||
| + | and $ L ^ \infty ( Q ) $, | ||
| + | the reverse implication being false in general (for even larger classes of statistical experiments, see, e.g., [[#References|[a6]]]). However, every coherent experiment is weakly dominated (and vice versa) in the following sense [[#References|[a7]]]: there exists a semi-finite (not $ \sigma $- | ||
| + | finite, in general) and localizable [[#References|[a11]]] measure $ \mu $ | ||
| + | on $ ( \Omega, {\mathcal F} ) $ | ||
| + | such that for $ A \in {\mathcal F} $ | ||
| + | one has $ \mu ( A ) = 0 $ | ||
| + | if and only if $ P ( A ) = 0 $ | ||
| + | for all $ P \in {\mathcal P} $. | ||
| + | This result is an alternative interpretation of the fact that $ L ^ \infty ( \mu ) $ | ||
| + | is isomorphic to $ [ L ^ {1} ( \mu ) ] ^ {*} $ | ||
| + | if and only if $ \mu $ | ||
| + | is semi-finite and localizable [[#References|[a11]]]. | ||
| + | |||
| + | The experiment $ {\mathcal E} = ( \Omega, {\mathcal F}, {\mathcal P} ) $ | ||
| + | with $ \Omega = [ 0,1 ] $, | ||
| + | $ {\mathcal F} $ | ||
| + | the Borel field, and $ {\mathcal P} = \{ {\delta _ {x} } : {x \in [ 0,1 ] } \} $ | ||
| + | is not coherent, since the counting measure $ \mu $ | ||
| + | is not localizable on $ {\mathcal F} $ | ||
| + | because $ {\mathcal F} $ | ||
| + | is countably generated but $ \mu $ | ||
| + | is not $ \sigma $- | ||
| + | finite [[#References|[a6]]] (this argument needs the assumption that each uncountable metric space contains a non-Borel set). | ||
====References==== | ====References==== | ||
<table><TR><TD valign="top">[a1]</TD> <TD valign="top"> I.M. Bomze, "A functional analytic approach to statistical experiments" , Longman (1990)</TD></TR><TR><TD valign="top">[a2]</TD> <TD valign="top"> H. Heyer, "Theory of statistical experiments" , Springer (1982)</TD></TR><TR><TD valign="top">[a3]</TD> <TD valign="top"> S. Kakutani, "Concrete representation of abstract <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/l/l110/l110030/l110030104.png" />-spaces and the mean ergodic theorem" ''Ann. of Math.'' , '''42''' (1941) pp. 523–537</TD></TR><TR><TD valign="top">[a4]</TD> <TD valign="top"> L. Le Cam, "Sufficiency and approximate sufficiency" ''Ann. Math. Stat.'' , '''35''' (1964) pp. 1419–1455</TD></TR><TR><TD valign="top">[a5]</TD> <TD valign="top"> L. Le Cam, "Asymptotic methods in statistical decision theory" , Springer (1986)</TD></TR><TR><TD valign="top">[a6]</TD> <TD valign="top"> H. Luschgy, D. Mussmann, "Products of majorized experiments" ''Statistics and Decision'' , '''4''' (1986) pp. 321–335</TD></TR><TR><TD valign="top">[a7]</TD> <TD valign="top"> E. Siebert, "Pairwise sufficiency" ''Z. Wahrscheinlichkeitsth. verw. Gebiete'' , '''46''' (1979) pp. 237–246</TD></TR><TR><TD valign="top">[a8]</TD> <TD valign="top"> H. Strasser, "Mathematical theory of statistics" , de Gruyter (1985)</TD></TR><TR><TD valign="top">[a9]</TD> <TD valign="top"> E.N. Torgersen, "On complete sufficient statistics and uniformly minimum variance unbiased estimators" ''Teoria statistica delle decisioni. Symp. Math.'' , '''25''' (1980) pp. 137–153</TD></TR><TR><TD valign="top">[a10]</TD> <TD valign="top"> E.N. Torgersen, "Comparison of statistical experiments" , Cambridge Univ. Press (1991)</TD></TR><TR><TD valign="top">[a11]</TD> <TD valign="top"> A.C. Zaanen, "Integration" , North-Holland (1967)</TD></TR></table> | <table><TR><TD valign="top">[a1]</TD> <TD valign="top"> I.M. Bomze, "A functional analytic approach to statistical experiments" , Longman (1990)</TD></TR><TR><TD valign="top">[a2]</TD> <TD valign="top"> H. Heyer, "Theory of statistical experiments" , Springer (1982)</TD></TR><TR><TD valign="top">[a3]</TD> <TD valign="top"> S. Kakutani, "Concrete representation of abstract <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/l/l110/l110030/l110030104.png" />-spaces and the mean ergodic theorem" ''Ann. of Math.'' , '''42''' (1941) pp. 523–537</TD></TR><TR><TD valign="top">[a4]</TD> <TD valign="top"> L. Le Cam, "Sufficiency and approximate sufficiency" ''Ann. Math. Stat.'' , '''35''' (1964) pp. 1419–1455</TD></TR><TR><TD valign="top">[a5]</TD> <TD valign="top"> L. Le Cam, "Asymptotic methods in statistical decision theory" , Springer (1986)</TD></TR><TR><TD valign="top">[a6]</TD> <TD valign="top"> H. Luschgy, D. Mussmann, "Products of majorized experiments" ''Statistics and Decision'' , '''4''' (1986) pp. 321–335</TD></TR><TR><TD valign="top">[a7]</TD> <TD valign="top"> E. Siebert, "Pairwise sufficiency" ''Z. Wahrscheinlichkeitsth. verw. Gebiete'' , '''46''' (1979) pp. 237–246</TD></TR><TR><TD valign="top">[a8]</TD> <TD valign="top"> H. Strasser, "Mathematical theory of statistics" , de Gruyter (1985)</TD></TR><TR><TD valign="top">[a9]</TD> <TD valign="top"> E.N. Torgersen, "On complete sufficient statistics and uniformly minimum variance unbiased estimators" ''Teoria statistica delle decisioni. Symp. Math.'' , '''25''' (1980) pp. 137–153</TD></TR><TR><TD valign="top">[a10]</TD> <TD valign="top"> E.N. Torgersen, "Comparison of statistical experiments" , Cambridge Univ. Press (1991)</TD></TR><TR><TD valign="top">[a11]</TD> <TD valign="top"> A.C. Zaanen, "Integration" , North-Holland (1967)</TD></TR></table> | ||
Revision as of 22:15, 5 June 2020
An order-complete Banach lattice (cf. also Riesz space) of measures on a measurable space $ ( \Omega, {\mathcal F} ) $,
defined in the context of statistical decision theory [a2], [a5], [a7], [a8], [a10]. Prime object of this theory is the statistical experiment $ {\mathcal E} = ( \Omega, {\mathcal F}, {\mathcal P} ) $
where $ {\mathcal P} $
is a set of probability measures on $ ( \Omega, {\mathcal F} ) $.
A statistical decision problem is to determine which of the distributions in $ {\mathcal P} $
are most likely to generate the observations (or data) collected. While the Radon–Nikodým theorem guarantees that one can operate with densities
$$ { \frac{dP }{d \mu } } \in L _ {1} ( \mu ) $$
of distributions if all $ P \in {\mathcal P} $ are dominated by a $ \sigma $- finite measure $ \mu $ on $ ( \Omega, {\mathcal F} ) $, there is no such possibility in the undominated case. Nevertheless, there is a substitute for the space generated by the $ { {dP } / {d \mu } } $ which respects both the linear and the order structure of measures: the $ L $- space $ L ( {\mathcal E} ) $ of the experiment, introduced in [a4]. This is a subspace of the Banach lattice of all signed measures on $ ( \Omega, {\mathcal F} ) $, and can be defined in three different ways, as follows [a1].
Denote by $ { \mathop{\rm ca} } ( \Omega, {\mathcal F} ) $ the vector lattice of all signed finite measures on $ ( \Omega, {\mathcal F} ) $, put $ | \mu | = \sup ( \mu, - \mu ) \in { \mathop{\rm ca} } ( \Omega, {\mathcal F} ) $ and use $ \mu \perp \nu $ as an abbreviation for $ \inf ( | \mu | , | \nu | ) = 0 $. Equipped with the variational norm $ \| \mu \| = | \mu | ( \Omega ) $, $ { \mathop{\rm ca} } ( \Omega, {\mathcal F} ) $ is an order-complete Banach lattice. More precisely, $ { \mathop{\rm ca} } ( \Omega, {\mathcal F} ) $ is an abstract $ L $- space, which means that the norm $ \| \cdot \| $ is additive on $ { \mathop{\rm ca} } ( \Omega, {\mathcal F} ) _ {+} $. A solid linear subspace $ {\mathcal D} \subseteq { \mathop{\rm ca} } ( \Omega, {\mathcal F} ) $ is called a band if $ \sup _ {i \in I } \mu _ {i} \in {\mathcal D} $ whenever the $ \mu _ {i} \in {\mathcal D} $ satisfy $ \mu _ {i} \leq \mu \in { \mathop{\rm ca} } ( \Omega, {\mathcal F} ) $ for all $ i \in I $.
If $ {\mathcal E} = ( \Omega, {\mathcal F}, {\mathcal P} ) $ is a statistical experiment, then one defines
a) $ L _ {1} ( {\mathcal E} ) $ to be the smallest band (with respect to $ \subseteq $) in $ { \mathop{\rm ca} } ( \Omega, {\mathcal F} ) $ containing $ {\mathcal P} $;
b) $ L _ {2} ( {\mathcal E} ) $ to be the $ \| \cdot \| $- closure of $ L ^ \prime ( {\mathcal E} ) $, where
$$ L ^ \prime ( {\mathcal E} ) = \left \{ {\mu \in { \mathop{\rm ca} } ( \Omega, {\mathcal F} ) } : \left | \mu \right | \leq \sum _ {i = 1 } ^ { n } \alpha _ {i} P _ {i} \right . $$
$$ \left . {\textrm{ for some } P _ {i} \in {\mathcal P}, \alpha _ {i} \geq 0, \textrm{ all } i ; n \in \mathbf N } \right \} ; $$
c) $ L _ {3} ( {\mathcal E} ) = \{ {\mu \in { \mathop{\rm ca} } ( \Omega, {\mathcal F} ) } : {\mu \perp \sigma \textrm{ for all } \sigma \perp {\mathcal P} } \} $. Then $ L _ {1} ( {\mathcal E} ) = L _ {2} ( {\mathcal E} ) = L _ {3} ( {\mathcal E} ) $. This space is called the $ L $- space of $ {\mathcal E} $ and is denoted by $ L ( {\mathcal E} ) $.
If there exists a $ Q \in { \mathop{\rm ca} } ( \Omega, {\mathcal F} ) $ such that for $ A \in {\mathcal F} $ one has $ Q ( A ) = 0 $ if and only if $ P ( A ) = 0 $ for all $ P \in {\mathcal P} $, then $ {\mathcal E} $ is dominated (and vice versa). In this case, the $ L $- space $ L ( {\mathcal E} ) $ of $ {\mathcal E} $ is, as a Banach lattice, isomorphic to $ L ^ {1} ( Q ) $. The situation for undominated experiments is different. As an abstract $ L $- space, $ L ( {\mathcal E} ) $ is always isomorphic to $ L ^ {1} ( m ) $, with $ m $ a Radon measure on a locally compact topological space [a3]. However, in general $ m $ is not even semi-finite [a6] (i.e., lacks the finite subset property [a11]), and then there is no representation of the topological dual $ M ( {\mathcal E} ) = L ( {\mathcal E} ) ^ {*} $ as $ L ^ \infty ( m ) $. $ M ( {\mathcal E} ) $ is called the $ M $- space of the experiment $ {\mathcal E} $ and generalizes the space of equivalence classes of bounded random variables in the following sense. Let $ X $ denote the set of all real-valued functions defined on $ \Omega $ that are $ {\mathcal F} $- measurable and bounded. For any $ \varphi \in X $, denote by $ {\dot \varphi } $ the mapping assigning $ \int _ \Omega \varphi {d \mu } $ to every $ \mu \in L ( {\mathcal E} ) $. Then $ M ( {\mathcal E} ) $ coincides with the $ \sigma ( M ( {\mathcal E} ) ,L ( {\mathcal E} ) ) $- closure of $ {\dot{X} } $[a1], [a4], [a8]. For an alternative representation of $ M ( {\mathcal E} ) $, see [a9].
An experiment $ {\mathcal E} $ is called coherent if $ M ( {\mathcal E} ) = {\dot{X} } $. Every dominated experiment is also coherent, due to the familiar isomorphism between $ [ L ^ {1} ( Q ) ] ^ {*} $ and $ L ^ \infty ( Q ) $, the reverse implication being false in general (for even larger classes of statistical experiments, see, e.g., [a6]). However, every coherent experiment is weakly dominated (and vice versa) in the following sense [a7]: there exists a semi-finite (not $ \sigma $- finite, in general) and localizable [a11] measure $ \mu $ on $ ( \Omega, {\mathcal F} ) $ such that for $ A \in {\mathcal F} $ one has $ \mu ( A ) = 0 $ if and only if $ P ( A ) = 0 $ for all $ P \in {\mathcal P} $. This result is an alternative interpretation of the fact that $ L ^ \infty ( \mu ) $ is isomorphic to $ [ L ^ {1} ( \mu ) ] ^ {*} $ if and only if $ \mu $ is semi-finite and localizable [a11].
The experiment $ {\mathcal E} = ( \Omega, {\mathcal F}, {\mathcal P} ) $ with $ \Omega = [ 0,1 ] $, $ {\mathcal F} $ the Borel field, and $ {\mathcal P} = \{ {\delta _ {x} } : {x \in [ 0,1 ] } \} $ is not coherent, since the counting measure $ \mu $ is not localizable on $ {\mathcal F} $ because $ {\mathcal F} $ is countably generated but $ \mu $ is not $ \sigma $- finite [a6] (this argument needs the assumption that each uncountable metric space contains a non-Borel set).
References
| [a1] | I.M. Bomze, "A functional analytic approach to statistical experiments" , Longman (1990) |
| [a2] | H. Heyer, "Theory of statistical experiments" , Springer (1982) |
| [a3] | S. Kakutani, "Concrete representation of abstract 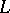 -spaces and the mean ergodic theorem" Ann. of Math. , 42 (1941) pp. 523–537 -spaces and the mean ergodic theorem" Ann. of Math. , 42 (1941) pp. 523–537 |
| [a4] | L. Le Cam, "Sufficiency and approximate sufficiency" Ann. Math. Stat. , 35 (1964) pp. 1419–1455 |
| [a5] | L. Le Cam, "Asymptotic methods in statistical decision theory" , Springer (1986) |
| [a6] | H. Luschgy, D. Mussmann, "Products of majorized experiments" Statistics and Decision , 4 (1986) pp. 321–335 |
| [a7] | E. Siebert, "Pairwise sufficiency" Z. Wahrscheinlichkeitsth. verw. Gebiete , 46 (1979) pp. 237–246 |
| [a8] | H. Strasser, "Mathematical theory of statistics" , de Gruyter (1985) |
| [a9] | E.N. Torgersen, "On complete sufficient statistics and uniformly minimum variance unbiased estimators" Teoria statistica delle decisioni. Symp. Math. , 25 (1980) pp. 137–153 |
| [a10] | E.N. Torgersen, "Comparison of statistical experiments" , Cambridge Univ. Press (1991) |
| [a11] | A.C. Zaanen, "Integration" , North-Holland (1967) |
L-space-of-a-statistical-experiment. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=L-space-of-a-statistical-experiment&oldid=14783