L-space-of-a-statistical-experiment
An order-complete Banach lattice (cf. also Riesz space) of measures on a measurable space 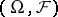 , defined in the context of statistical decision theory [a2], [a5], [a7], [a8], [a10]. Prime object of this theory is the statistical experiment
, defined in the context of statistical decision theory [a2], [a5], [a7], [a8], [a10]. Prime object of this theory is the statistical experiment  where
where 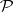 is a set of probability measures on
is a set of probability measures on 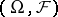 . A statistical decision problem is to determine which of the distributions in
. A statistical decision problem is to determine which of the distributions in 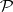 are most likely to generate the observations (or data) collected. While the Radon–Nikodým theorem guarantees that one can operate with densities
are most likely to generate the observations (or data) collected. While the Radon–Nikodým theorem guarantees that one can operate with densities
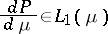 |
of distributions if all 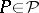 are dominated by a
are dominated by a 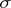 -finite measure
-finite measure 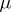 on
on 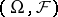 , there is no such possibility in the undominated case. Nevertheless, there is a substitute for the space generated by the
, there is no such possibility in the undominated case. Nevertheless, there is a substitute for the space generated by the  which respects both the linear and the order structure of measures: the
which respects both the linear and the order structure of measures: the 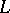 -space
-space 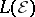 of the experiment, introduced in [a4]. This is a subspace of the Banach lattice of all signed measures on
of the experiment, introduced in [a4]. This is a subspace of the Banach lattice of all signed measures on 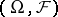 , and can be defined in three different ways, as follows [a1].
, and can be defined in three different ways, as follows [a1].
Denote by  the vector lattice of all signed finite measures on
the vector lattice of all signed finite measures on 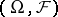 , put
, put 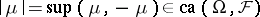 and use
and use 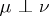 as an abbreviation for
as an abbreviation for 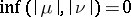 . Equipped with the variational norm
. Equipped with the variational norm  ,
,  is an order-complete Banach lattice. More precisely,
is an order-complete Banach lattice. More precisely, 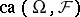 is an abstract
is an abstract 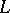 -space, which means that the norm
-space, which means that the norm  is additive on
is additive on 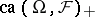 . A solid linear subspace
. A solid linear subspace 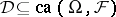 is called a band if
is called a band if 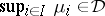 whenever the
whenever the 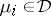 satisfy
satisfy 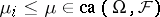 for all
for all 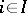 .
.
If 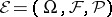 is a statistical experiment, then one defines
is a statistical experiment, then one defines
a) 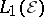 to be the smallest band (with respect to
to be the smallest band (with respect to  ) in
) in 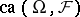 containing
containing 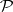 ;
;
b) 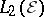 to be the
to be the  -closure of
-closure of 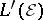 , where
, where
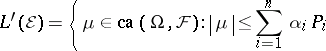 |
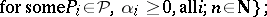 |
c) 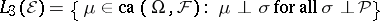 . Then
. Then 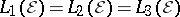 . This space is called the
. This space is called the 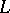 -space of
-space of 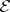 and is denoted by
and is denoted by 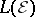 .
.
If there exists a 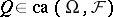 such that for
such that for  one has
one has 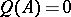 if and only if
if and only if 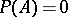 for all
for all 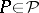 , then
, then 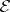 is dominated (and vice versa). In this case, the
is dominated (and vice versa). In this case, the 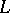 -space
-space  of
of 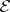 is, as a Banach lattice, isomorphic to
is, as a Banach lattice, isomorphic to 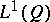 . The situation for undominated experiments is different. As an abstract
. The situation for undominated experiments is different. As an abstract 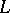 -space,
-space, 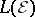 is always isomorphic to
is always isomorphic to 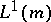 , with
, with 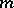 a Radon measure on a locally compact topological space [a3]. However, in general
a Radon measure on a locally compact topological space [a3]. However, in general 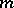 is not even semi-finite [a6] (i.e., lacks the finite subset property [a11]), and then there is no representation of the topological dual
is not even semi-finite [a6] (i.e., lacks the finite subset property [a11]), and then there is no representation of the topological dual 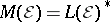 as
as 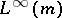 .
. 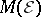 is called the
is called the 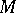 -space of the experiment
-space of the experiment 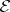 and generalizes the space of equivalence classes of bounded random variables in the following sense. Let
and generalizes the space of equivalence classes of bounded random variables in the following sense. Let 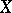 denote the set of all real-valued functions defined on
denote the set of all real-valued functions defined on  that are
that are 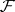 -measurable and bounded. For any
-measurable and bounded. For any 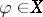 , denote by
, denote by 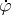 the mapping assigning
the mapping assigning 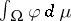 to every
to every 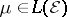 . Then
. Then  coincides with the
coincides with the  -closure of
-closure of 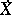 [a1], [a4], [a8]. For an alternative representation of
[a1], [a4], [a8]. For an alternative representation of 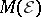 , see [a9].
, see [a9].
An experiment 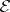 is called coherent if
is called coherent if 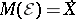 . Every dominated experiment is also coherent, due to the familiar isomorphism between
. Every dominated experiment is also coherent, due to the familiar isomorphism between 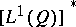 and
and 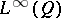 , the reverse implication being false in general (for even larger classes of statistical experiments, see, e.g., [a6]). However, every coherent experiment is weakly dominated (and vice versa) in the following sense [a7]: there exists a semi-finite (not
, the reverse implication being false in general (for even larger classes of statistical experiments, see, e.g., [a6]). However, every coherent experiment is weakly dominated (and vice versa) in the following sense [a7]: there exists a semi-finite (not 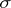 -finite, in general) and localizable [a11] measure
-finite, in general) and localizable [a11] measure  on
on 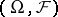 such that for
such that for 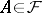 one has
one has 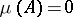 if and only if
if and only if 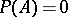 for all
for all 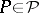 . This result is an alternative interpretation of the fact that
. This result is an alternative interpretation of the fact that 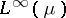 is isomorphic to
is isomorphic to 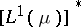 if and only if
if and only if 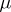 is semi-finite and localizable [a11].
is semi-finite and localizable [a11].
The experiment 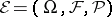 with
with 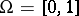 ,
, 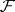 the Borel field, and
the Borel field, and 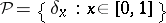 is not coherent, since the counting measure
is not coherent, since the counting measure 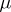 is not localizable on
is not localizable on 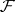 because
because 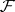 is countably generated but
is countably generated but  is not
is not 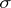 -finite [a6] (this argument needs the assumption that each uncountable metric space contains a non-Borel set).
-finite [a6] (this argument needs the assumption that each uncountable metric space contains a non-Borel set).
References
| [a1] | I.M. Bomze, "A functional analytic approach to statistical experiments" , Longman (1990) |
| [a2] | H. Heyer, "Theory of statistical experiments" , Springer (1982) |
| [a3] | S. Kakutani, "Concrete representation of abstract 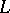 -spaces and the mean ergodic theorem" Ann. of Math. , 42 (1941) pp. 523–537 -spaces and the mean ergodic theorem" Ann. of Math. , 42 (1941) pp. 523–537 |
| [a4] | L. Le Cam, "Sufficiency and approximate sufficiency" Ann. Math. Stat. , 35 (1964) pp. 1419–1455 |
| [a5] | L. Le Cam, "Asymptotic methods in statistical decision theory" , Springer (1986) |
| [a6] | H. Luschgy, D. Mussmann, "Products of majorized experiments" Statistics and Decision , 4 (1986) pp. 321–335 |
| [a7] | E. Siebert, "Pairwise sufficiency" Z. Wahrscheinlichkeitsth. verw. Gebiete , 46 (1979) pp. 237–246 |
| [a8] | H. Strasser, "Mathematical theory of statistics" , de Gruyter (1985) |
| [a9] | E.N. Torgersen, "On complete sufficient statistics and uniformly minimum variance unbiased estimators" Teoria statistica delle decisioni. Symp. Math. , 25 (1980) pp. 137–153 |
| [a10] | E.N. Torgersen, "Comparison of statistical experiments" , Cambridge Univ. Press (1991) |
| [a11] | A.C. Zaanen, "Integration" , North-Holland (1967) |
L-space-of-a-statistical-experiment. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=L-space-of-a-statistical-experiment&oldid=14783